查找

一、 查找的基本概论

查找：在数据集中寻找满足某条件的数据元素的过程叫查找

查找表：用于查找的数据集合称为查找表，它由同一类型的数据元素
（或记录）组成，可以是一个数组或者链表等数据类型。
静态、动态查找表：是否再新增或者删除元素

关键字：数据元素中唯一标识该元素的某个数据项的值，使用基于关键字的查找，查找的结果应该是唯一的。

平均查找长度：在查找的过程中，一次查找的长度是指需要比较的关键字的次数，而平均查找长度则是所有查找过程中进行关键字的比较的次数的平均值。
$ASL={\sum }_{i=1}^{n}PiCi$
一般认为$Pi=\frac{1}{n}$
Ci为第 i 个数据元素所需进行的比较次数

二、 线性表的查找

2.1 顺序查找

2.1.1 一般表顺序查找

2.1.1.1 定义

2.1.1.2 结构体

typedef struct{			//查找表
	ElemType *elem;		//动态数组基址
	int TableLen;       //表的长度
}SSTable;

2.1.1.3 代码

int Search_Seq(SSTable ST,ElemType key){
	ST.elem[0] = key;						//哨兵
	int i;
	for(i=ST.TableLen;ST.elem[i]!=key;--i);
	return i;
}

2.1.2 有序表查找优化

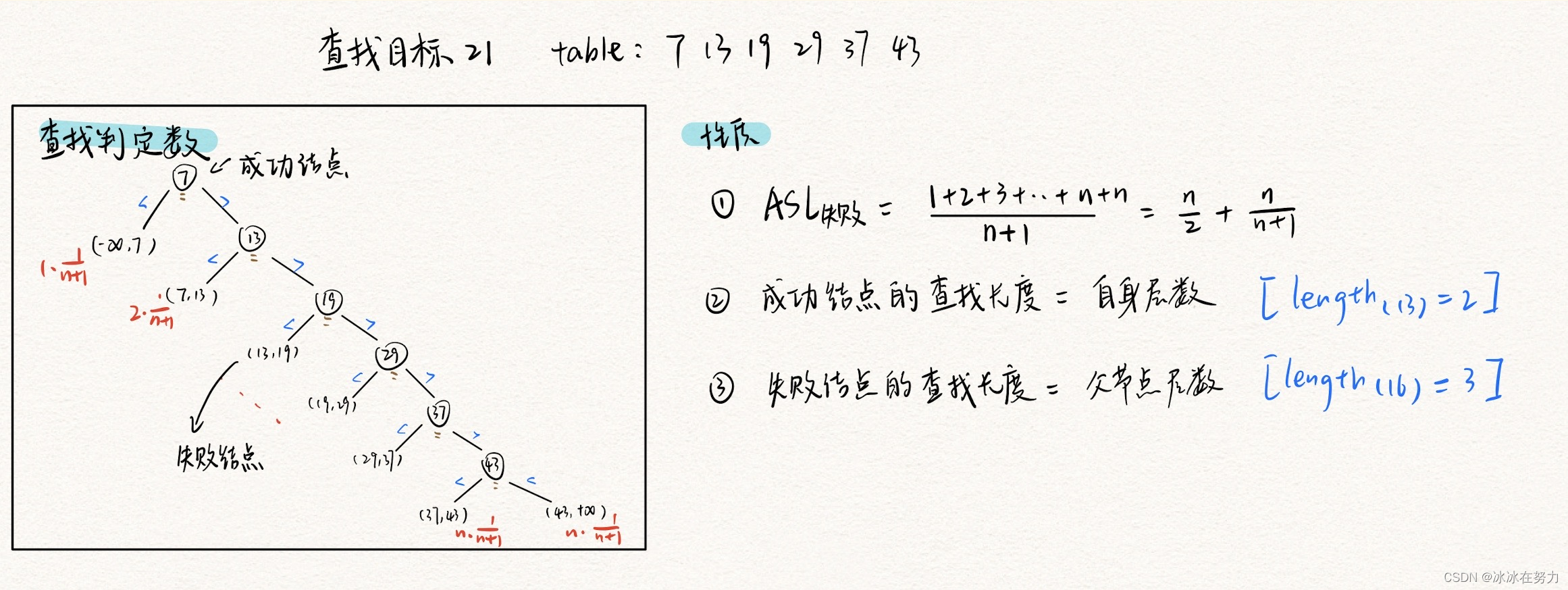
2.2 折半查找

2.2.1 算法思想

2.2.2 代码实现

typedef struct{
	ElemType *elem;		//动态数组基址 
	int TableLen;		//表的长度 
}SSTable; 

int Binary_Search(SSTable L,ElemType key){
	int low=0,high=L.TableLen-1,mid;
	while(low<=high){
		mid = (low+high)/2;
		if(L.elem[mid] == key) return mid;		//查找成功 
		else if(L.elem[mid]>key) high=mid-1;	//去左边查找 
		else low=mid+1;							//去右边查找 
	}
	return -1;									//查找失败 
} 

2.2.3 查找效率

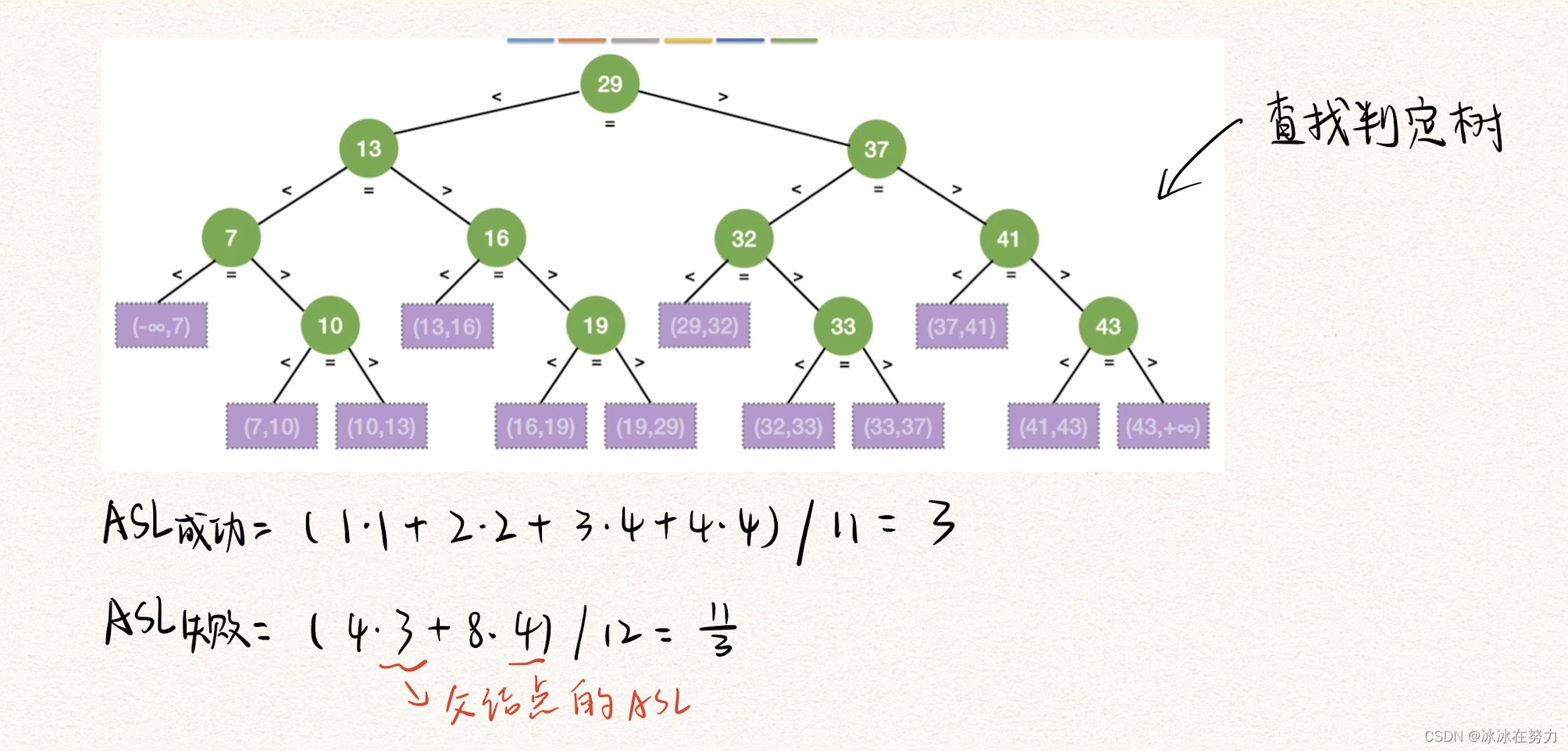
2.2.4 折半查找判定树

• 折半查找树是平衡二叉树（左右子树高度之差不大于1）
• 折半查找判定树可以用二叉排序树来判别，其中序序列是一个有序序列
• 还有可能要判断取整方向是否一致【一致向上取整还是一致向下取整，见17年408题第8题】
  

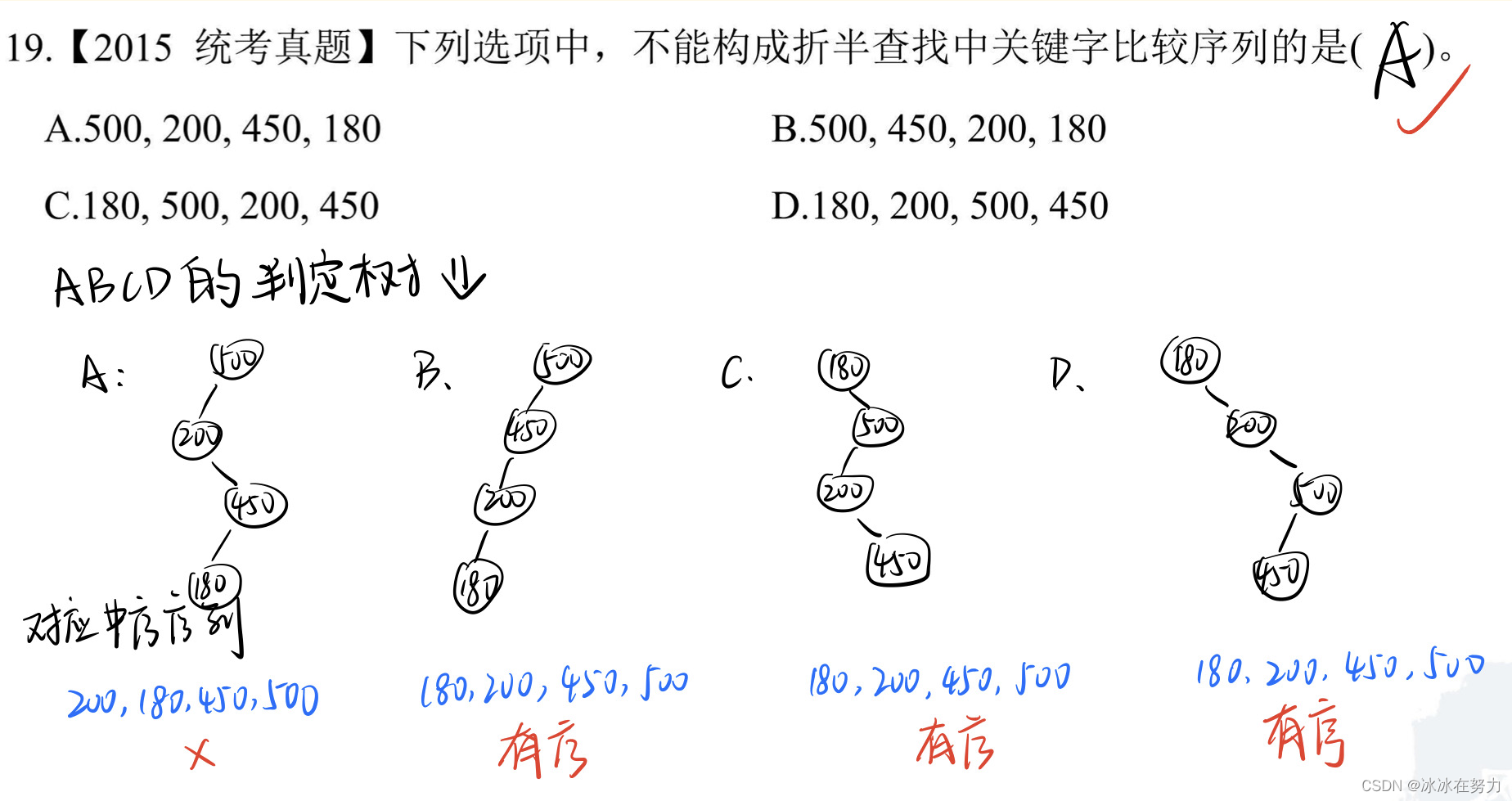
2.2.5 结论

• 树的高度$h=\lfloor (lo{g}_{2}n)+1\rfloor =\lceil (lo{g}_{2}n+1)\rceil$
• 时间复杂度为$O(lo{g}_{2}n)$
• 查找不成功时比较次数最多即为高度h，注意最后一个数也要比较，不要忘记了
• 折半查找和二叉排序树最好的情况时平均查找长度都是$O(lo{g}_{2}n)$
• 二叉排序树最坏的情况形成单支树，查找长度为$O(n)$

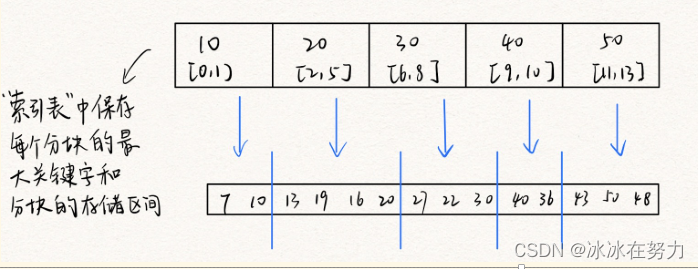
2.3 分块查找

2.3.1 算法思想

2.3.2 结构体

typedef struct{
	ElemType maxValue;
	int low,high;
}Index;
ElemType List[100];

2.3.3 效率分析

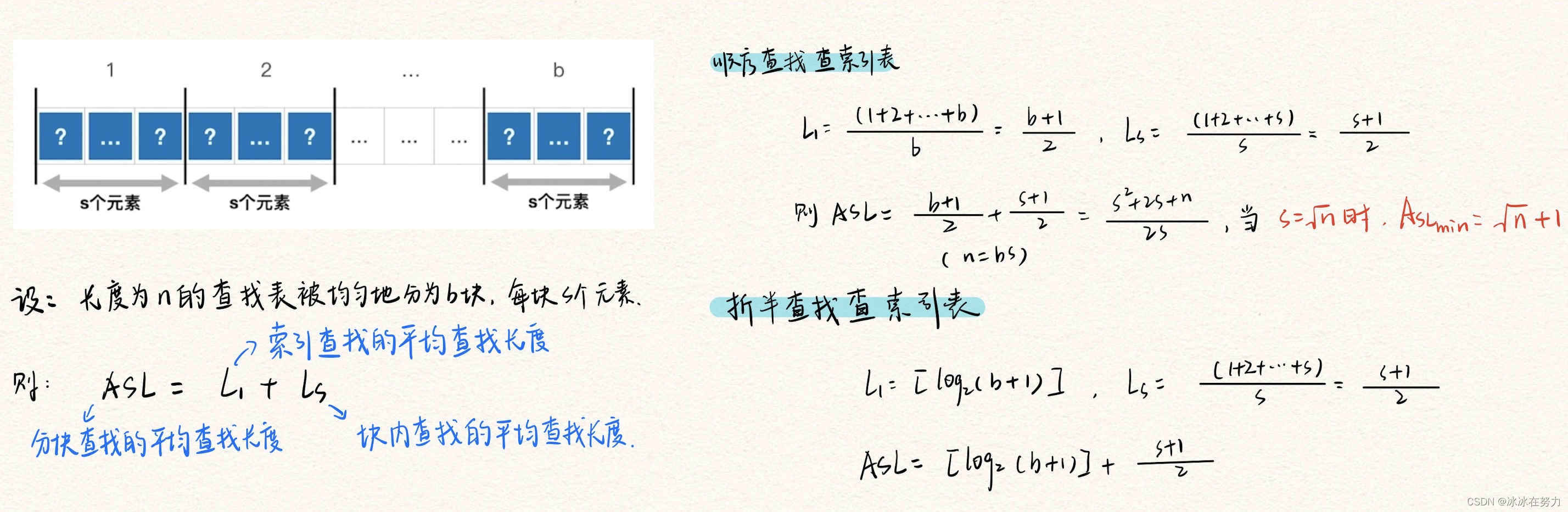
2.3.4 结论

• 顺序查找效率最快时， 块数=$\sqrt{n}$
• 数据分成若干块，每块内数据不必有序，但块间必须有序，但块内最大/最小的数据组成索引块

三、 树表的查找

3.1 二叉排序树BST

3.1.1 二叉排序树的定义

二叉排序树或者是一棵空树，或者是一棵具有下列特性的非空二叉树：

1. 若左子树非空，则左子树上所有结点关键字均小于根结点的关键字值；
2. 若右子树非空，则右子树上所有结点关键字均大于根结点的关键字值；
3. 左、右子树本身也分别是一棵二叉排序树。

二叉排序树是一个递归的数据结构
二叉排序树进行中序遍历，可以得到一个递增的有序序列

//结构体
typedef struct BSTNode{
    int data;
    struct BSTNode *left;
    struct BSTNode *right;
}BSTNode;

//二叉树结点创建
BSTNode *CreateTreeNode(int x){
    BSTNode *p = (BSTNode *)malloc(sizeof(BSTNode));
    p->data = x;
    p->left = NULL;
    p->right = NULL;
    return p;
}

3.1.2 二叉排序树的查找

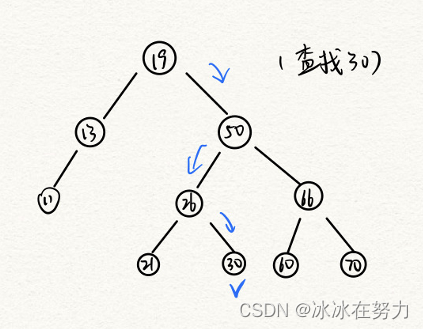
//查找的递归算法
BSTNode *Search(BSTNode *root, int x){
    if(root->data == x){
        return root;
    }else if(x < root->data){
        return Search(root->left, x);
    }else{
        return Search(root->right, x);
    }
}

//查找的非递归算法
BSTNode *Search(BSTNode *root, int x){
    BSTNode *p = root;
    while(p!=NULL && p->data!=x){
        if(x < p->data)
            p = p->left;
        else
            p = p->right;
    }
    return p;
}

3.1.3 二叉排序树的插入

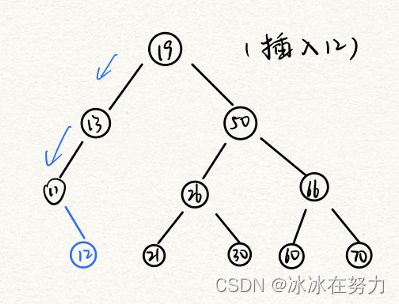
//插入的递归算法
BSTNode *Insert(BSTNode *root, int x){
    if(root == NULL){
        root = CreateTreeNode(x);
        return root;
    }
    if(x < root->data){
        root->left = Insert(root->left, x);
    }
    if(x > root->data){
        root->right = Insert(root->right, x);
    }
    return root;
}

//插入的非递归算法
BSTNode *Insert1(BSTNode *root, int x){
    BSTNode *parent = NULL;
    BSTNode *p = root;
    if(root == NULL){
        root = CreateTreeNode(x);
        return root;
    }
    while(p != NULL){
        parent = p;
        if(x < p->data){
            p = p->left;
        }else{
            p = p->right;
        }
    }
    if(parent->data >x){
        parent->left = CreateTreeNode(x);
    }else{
        parent->right = CreateTreeNode(x);
    }
    return root;
}

3.1.4 二叉排序树的创建

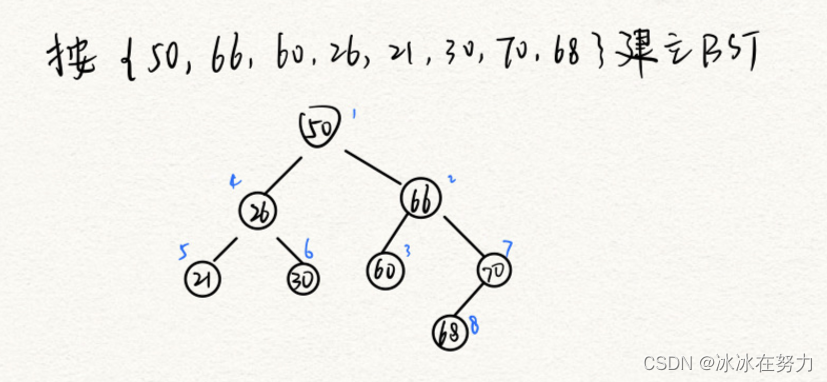
void Create(BSTNode *&root, int str[], int n){
    root = NULL;
    for(int i=0; i<n; i++){
        Insert(root, str[i]);
    }
}

3.1.5 二叉排序树的删除

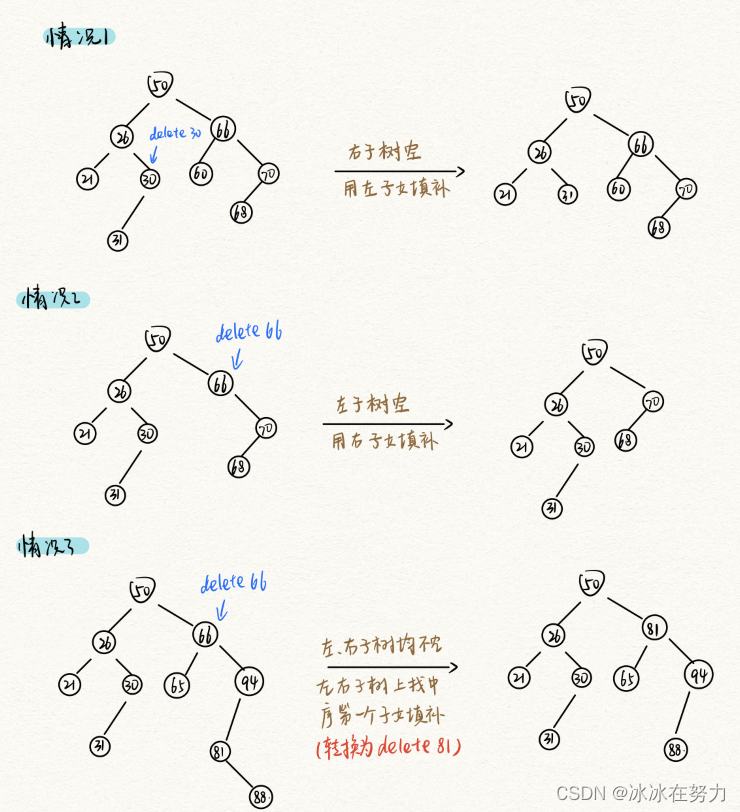
3.2 平衡二叉树ALV

3.2.1 定义

1. 平衡二叉树是「二叉排序树」
2. 任何一个节点的左子树或者右子树都是「平衡二叉树」（左右高度差小于等于 1）
3. 平衡因子 BF：左子树和右子树高度差
4. 最小不平衡子树：距离插入节点最近的，并且 BF 的绝对值大于 1 的节点为根节点的子树。

3.2.2 四种旋转方式

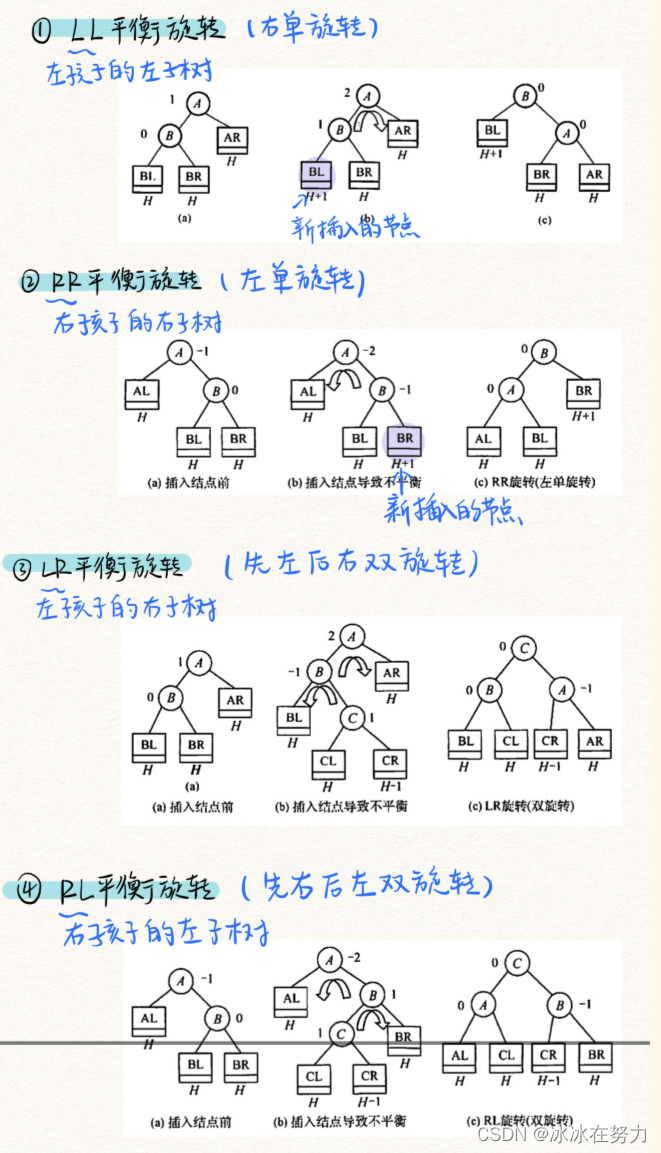
3.2.3 例子

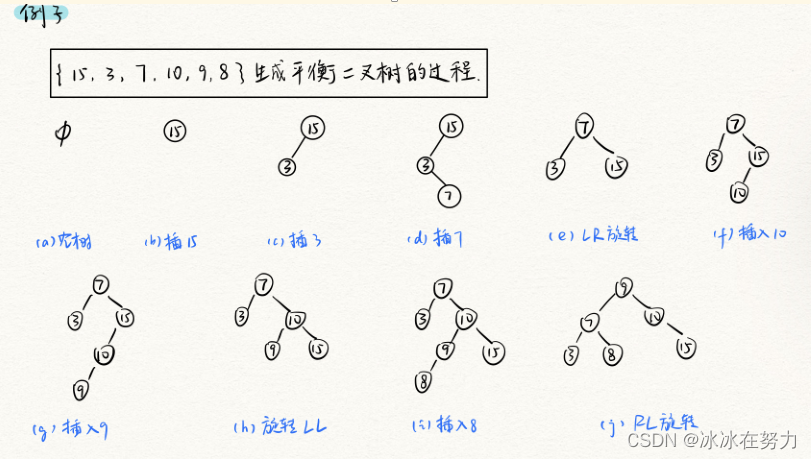
3.2.4 平衡二叉树的查找

3.2.5 平衡二叉树的删除

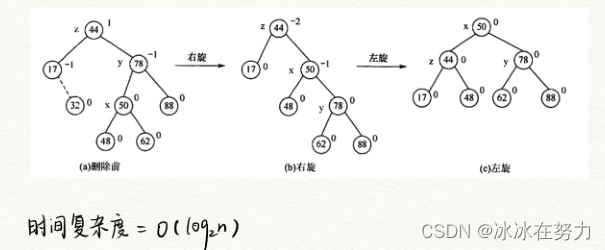
3.3 B 树

3.3.1 B树的相关概念

• 一棵m阶B树(balanced tree of order m)是一棵平衡的m路搜索树。
• B树是一种自平衡树数据结构，它维护有序数据并允许以对数时间进行搜索，顺序访问，插入和删除
• B树是二叉搜索树的一般化，因为节点可以有两个以上的子节点
• B树非常适合读取和写入相对较大的数据块（如光盘）的存储系统；它通常用于数据库和文件系统
• B树中一个节点的子节点数目的最大值，用m表示，假如最大值为4，则为4阶，如图
  

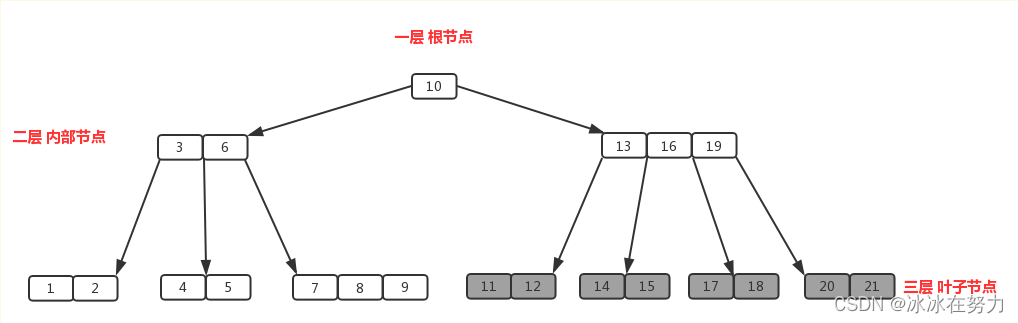
3.3.2 m阶的B树满足的条件

• 每个结点最多只有m棵子树
• 每个非叶子结点**(且非终端结点)**具有至少⌈ m/2 ⌉棵子树
• 根结点最多有m颗子树，至少2棵子树
• 具有k个子结点的非叶节点包含k-1个关键字
• 所有叶节点都在同一层次上
• 所有结点的关键字个数为⌈ m/2 ⌉-1$\le$n$\le$m-1

3.3.3 B树的查找

B-树的查找操作与二叉排序树（BST）极为类似，只不多 B-树中的每个结点包含多个关键字。假设待查找的关键字为 k ，我们从根结点开始，递归向下进行查找。对每一个访问的非叶子结点，如果结点包含待查找的关键字 k ，则返回结点指针；否则，我们递归到该结点的恰当子代（该子代结点中的关键字均在比 k 更大的关键字之前）。如果抵达了叶子结点且没有找到 k 则返回 null .

3.3.4 B树的插入

以中间关键词为界，把结点一分为二，成为两个结点，并把中间关键词向上插入到双亲结点上，若双亲结点已满，则采用同样的方法继续分解。最坏情况分解到树根结点，然后B树高度加一。

3.3.5 B树的删除

1. 删除记录后，关键词个数小于⌈ m/2 ⌉-1，就进行合并结点
2. 删除记录，还要删除该记录邻近的指针。

• 删的是最下层非终端结点，就直接删除
• 删的不是最下层非终端结点，将要删除记录用其右（左）边邻近指针指向的子树中关键词最小（大）的记录替换。（替换的记录必在最下层非终端结点中）

3.4 B+ 树

3.4.1 B+ 树的特征

• 有m个子树的中间节点包含有m个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引
• 所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针
• 叶子结点本身依关键字的大小自小而大的顺序链接
• 所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字

3.4.2 B+ 树的概念

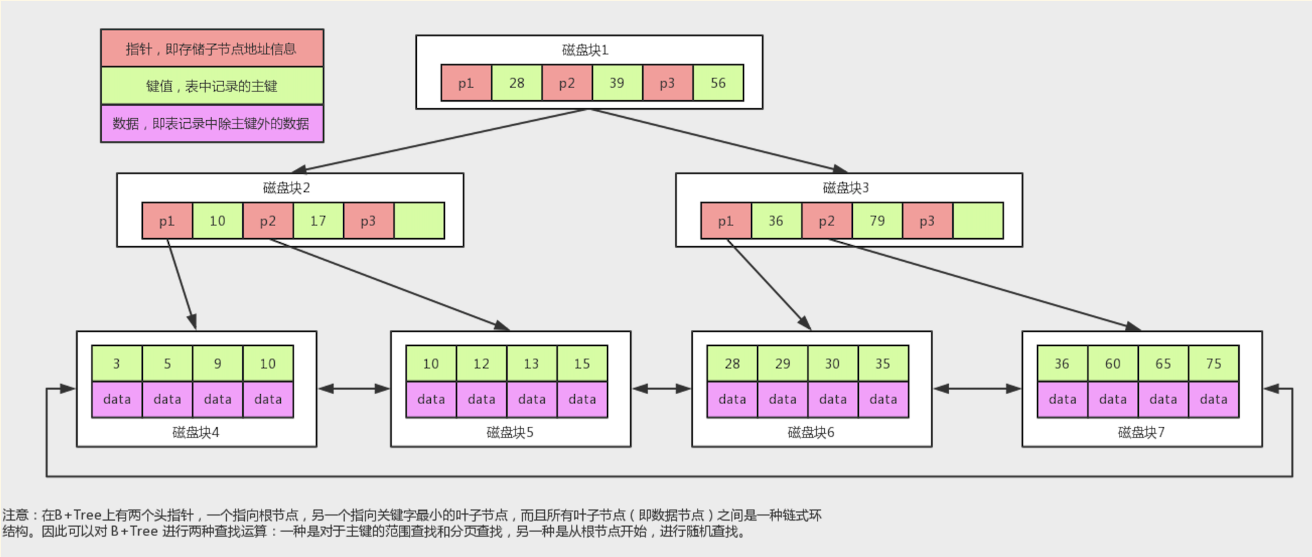
3.4.3 B树和B+ 树的对比

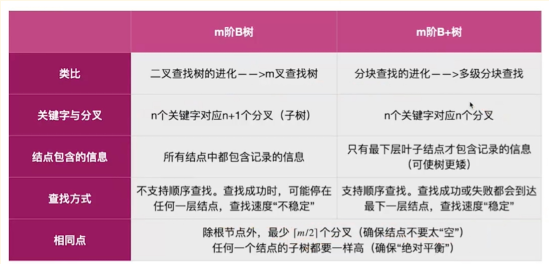
3.5 红黑树

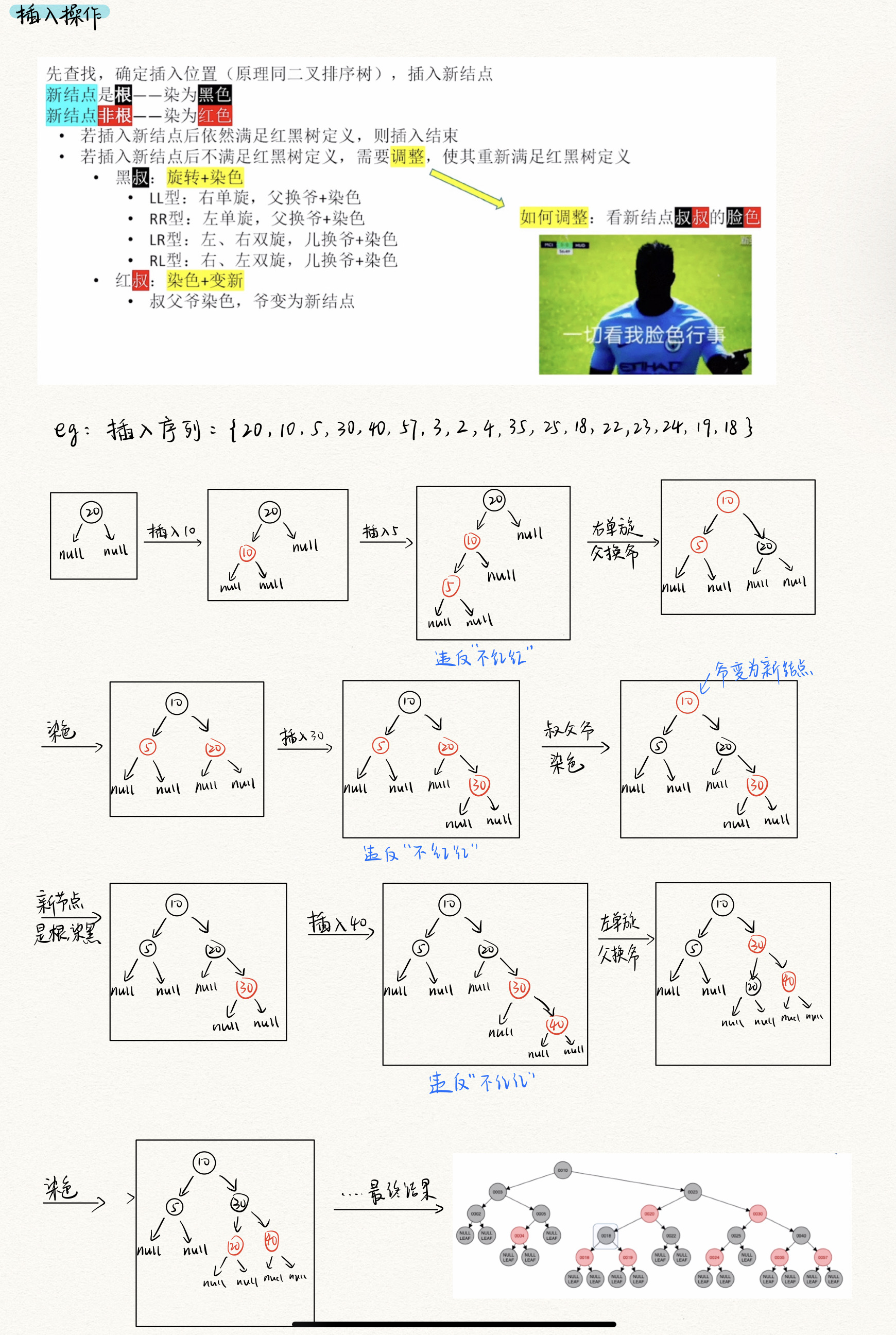
四、 散列表的查找

4.1 散列表的基本构造

• 散列查找一般适用于关键字集合与地址集合之间存在对应关系的情况下的查找
• 散列查找的思想是计算出散列地址来查找，然后比较关键字以确定是否比较成功
• 散列查找的平均查找长度与装填因子有关，与表长无关
• 装填因子=$\frac{表中记录数}{散列表长度}$
• 冲突是不可避免的，与装填因子无关
• 为提高查找效率可以：1. 设计冲突少的散列函数 2. 处理冲突时避免产生堆积现象 【装填因子是固有属性，不可变】
• 产生了堆积即产生了冲突，他对存储效率，散列函数和装填因子没有什么影响，但ASL会随堆积现象而增大
• 两项基本工作:
  • 计算位置：构造散列函数确定关键词存储位置
  • 解决冲突：应用某种策略解决多个关键词位置相同的问题

4.2 散列函数的构造方法

4.2.1 直接定址法

取关键字或关键字的某个线性函数值为散列地址。
即H(key) = key或H(key) = a·key + b，其中a和b为常数（这种散列函数叫做自身函数）。

4.2.2 数字分析法

适合处理关键字位数比较大的情况，如果事先知道关键字的分布且关键字的若干位分布比较均匀

• 分析数字关键字在各位上的变化情况
• 取比较随机的位作为散列地址
• 如电话号码、身份证号码某几位会比较随机

4.2.3 平方取中法

假设关键字是1234、平方之后是1522756、再抽取中间3位227，用作散列地址。平方取中法比较适合于不知道关键字的分布，而位数又不是很大的情况。

4.2.4 折叠法

将关键字从左到右分割成位数相等的几部分，最后一部分位数不够时可以短些，然后将这几部分叠加求和，并按散列表表长，取后几位作为散列地址。

比如关键字是9876543210，散列表表长是3位，将其分为四组，然后叠加求和：987 + 654 + 321 + 0 = 1962，取后3位962作为散列地址。

折叠法事先不需要知道关键字的分布，适合关键字位数较多的情况。

4.2.5 取留余数法

f(key) = key mod p (p≤m)，m为散列表长。这种方法不仅可以对关键字直接取模，也可在折叠、平方取中后再取模。根据经验，若散列表表长为m，通常p为小于或等于表长（最好接近m）的最小质数，可以更好的减小冲突。

此方法为最常用的构造散列函数方法。

4.2.6 随机数法

f(key) = random(key)，这里random是随机函数。当关键字的长度不等时，采用这个方法构造散列函数是比较合适的。

4.3 处理冲突的方法

4.3.1 开放地址法

• 一旦产生了冲突，就按某种规则去寻找另一空地址
• 发生聚集的原因主要是解决冲突的方法选择不当

4.3.1.1 线性探测

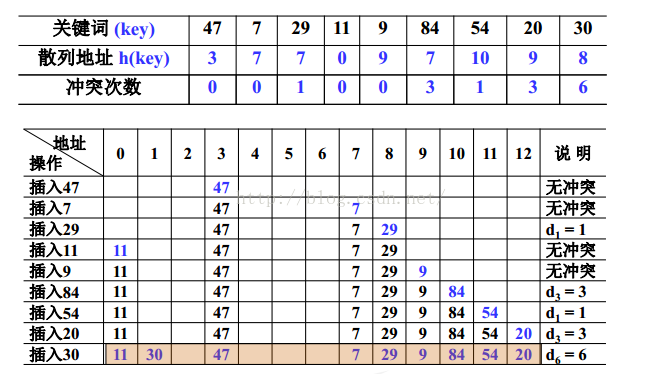
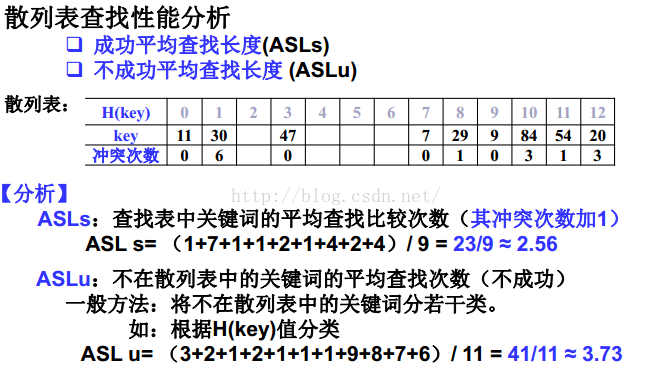
4.3.1.2 平方探测

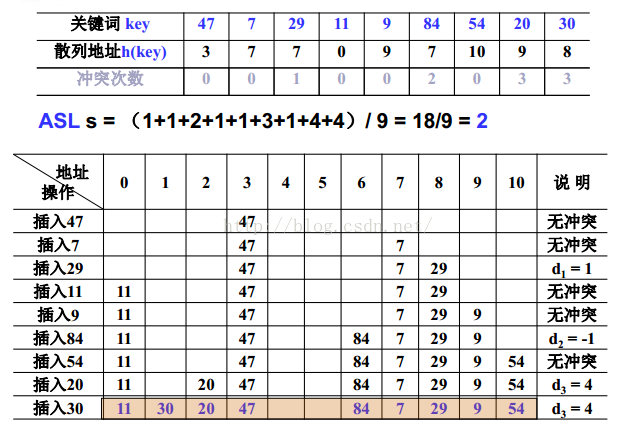
4.3.2 链地址法

将相应位置上冲突的所有关键词存储在同一个单链表中

五、参考

1. 二叉排序树的定义及基本操作（构造、查找、插入、删除）递归及非递归算法
2. 散列函数的6个构造方法