排序算法:存储桶排序算法
分组后,每个存储桶都会进行排序,然后将排序后的元素合并成一个有凝聚力的有序序列。桶排序的方法简化了排序过程,通过系统的桶分配和后续组织确保数据的有效排列。这将导致一个或多个存储桶比其他存储桶拥有更多元素,从而使存储桶排序像任何其他排序技术一样,其中每个元素都与另一个元素进行比较。或者,换句话说,数组的元素均匀分布在数组的整个跨度/范围内。范围内的元素数量相同。在这种情况下,我们将对每个存储桶的范围
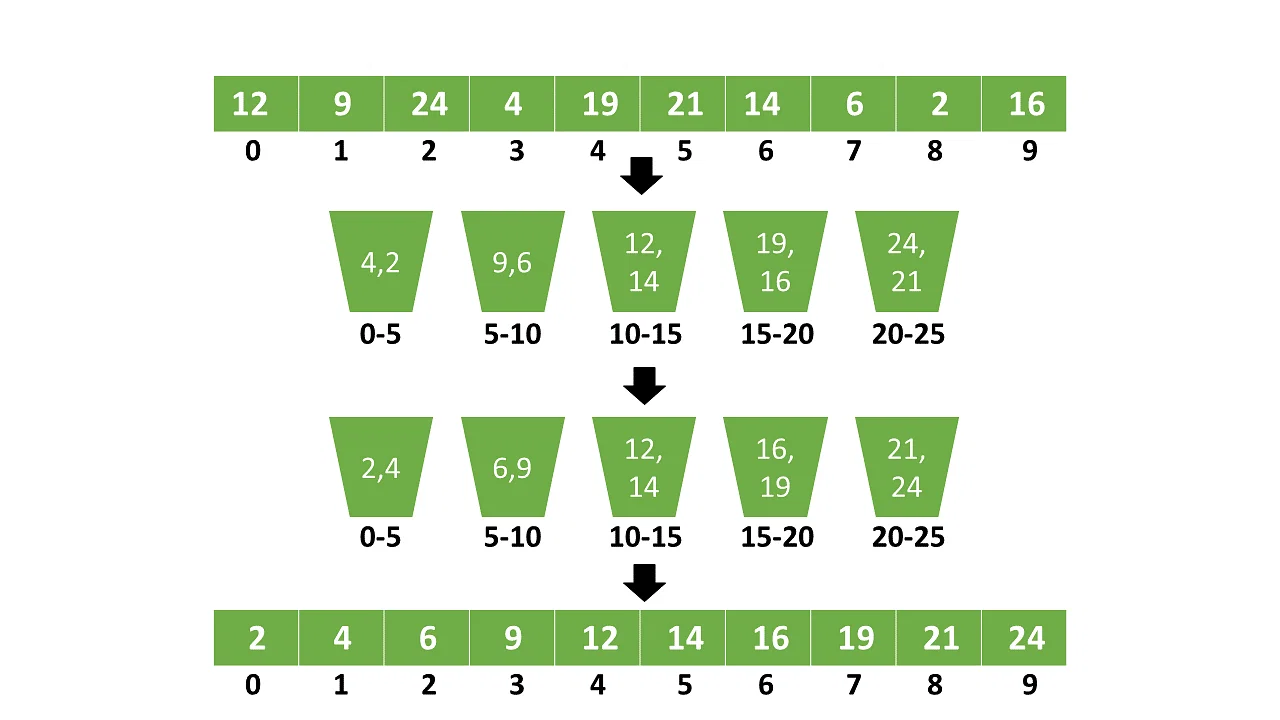
桶排序通过将元素分配到不同的桶中来有效地组织元素,从而便于使用替代算法进行后续排序。这项技术在软件工程面试中至关重要,它根据均匀分布将数据分类到不同的桶中。分组后,每个存储桶都会进行排序,然后将排序后的元素合并成一个有凝聚力的有序序列。桶排序的方法简化了排序过程,通过系统的桶分配和后续组织确保数据的有效排列。
均匀分布的数据
- 均匀分布的数据,每个相邻元素之间的差异几乎相同。
- 表示均匀分布数据的示例和图表。
如果数组内每个相邻元素之间的差异几乎相同,则称数组是均匀分布的。或者,换句话说,数组的元素均匀分布在数组的整个跨度/范围内。
例如:
-
考虑这个数组: [10, 21, 29, 41, 52] 每个相邻项之间的差几乎等于10。因此,该数组具有均匀分布的数据,并且可以使用桶排序算法进行排序。
-
考虑另一个数组: [1,4,23,5,44,9,6,43]该数组不是均匀分布的,因为范围[0-10] = 5 之间的元素数量(即1,4,5 、9 和 6 ),而[10-20]之间的元素数量为0 ,并且[30-40]范围内的元素数量相同。数据分散在不同的数据范围内,但集中在某些特定范围内,而其他范围内则稀疏。因此,该数组不是均匀分布的。
这就是均匀分布数据的样子:完整的数据均匀地分布在每个范围内,因此描述了均匀分布的数据。
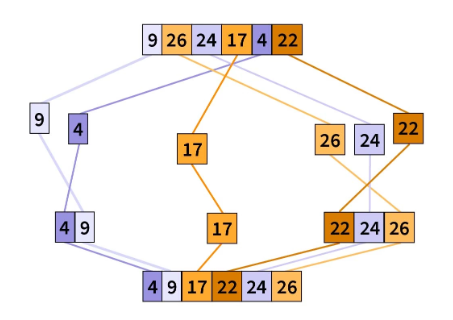
分散-聚集方法
解决大型且复杂的问题有时可能有点困难。分散聚集方法试图简化此类复杂问题,首先将完整数据分散到集群中,单独解决这些子问题,最后将它们聚集在一起以获得最终结果。这就是桶排序如何使用分散聚集方法:
桶排序算法
- 适用于均匀分布的数据
- 遵循分散-聚集方法
- 时间复杂度为O(n)的排序技术
桶排序是一种使用分散-聚集方法对数组进行排序的排序技术。
它将未排序的数组分为不同的组,并将它们称为存储桶。对各个存储桶进行排序,然后将它们全部聚集在一起形成最终的排序数组。
- 如果数组的元素是范围在0到1之间的浮点数,我们主要创建10 个桶,编号从0到9,然后根据其最高有效数字将元素插入到这些桶中。桶索引的计算方式为:(int) (elementNumber * 10)
- 如果数组的元素是整数,如下图所示,我们只需计算范围: range = (maximumNumber -minimumNumber) / noOfBuckets ,并将整个范围划分为多个桶,然后进行桶排序。
从图形上看,整数元素的桶排序如下所示:
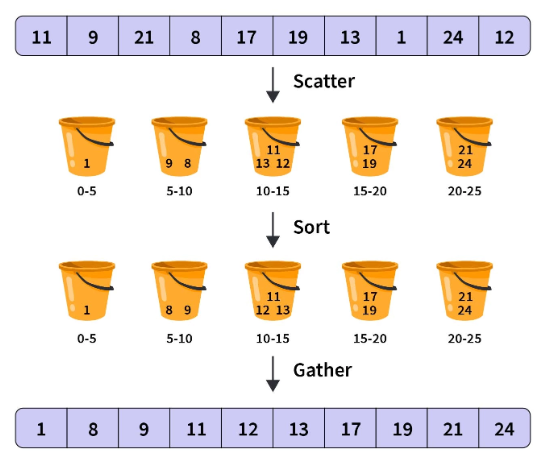
桶排序的工作原理
让我们借助上面的示例来了解该算法是如何工作的。考虑这个未排序的数组

步骤1:
由于我们的数组包含整数元素,因此我们将首先计算范围。
maximumElement = 24
minimumElement = 1
noOfBuckets = 5 (will be given as parameter)
range = (int)(24 - 1) / 5
= 4
因此,我们将拥有以下范围的存储桶: [1-5] [6-10] [11-15] [16-20] [21-25]

第 2 步:分散
现在,迭代未排序的数组,并继续将数字插入到其相应范围的存储桶中。
例如:
array[0] = 11, Range = [11-15]
array[1] = 9, Range = [6-10]
array[2] = 21, Range = [21-25]
array[3] = 8, Range = [6-10]
array[4] = 17, Range = [16-20]
等等..
最后,桶看起来像这样:
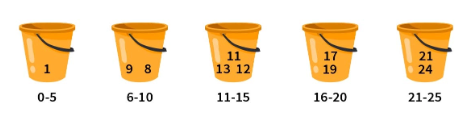
步骤3:
现在对每个桶中的所有元素进行排序,排序后的桶如下所示:
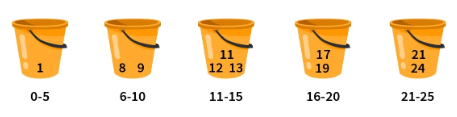
第四步:收集
最后,访问每个桶并将所有数字收集在一起。将它们全部合并,我们将得到排序后的数组。
因此,排序后的数组为:

伪代码
bucketSorting(arr, n):
Create n empty buckets
loop through each element of the arr and do the following
Calculate bucketIndex
Insert the element into the corresponding bucket number
3) Sort the individual buckets
4) Gather all the elements together
因此,我们得到了排序后的数组。
浮点数的桶排序算法
下面写的是桶排序的完整代码。
首先,我们创建一个向量bucket,然后在这个向量内创建n个bucket。然后遍历整个数组,将元素放入与其范围相对应的桶中。
JAVA代码
import java.util.*;
import java.util.Collections;
class Main {
// JAVA program to perform bucket sorting
// on array of size n
static void bucketSorting(float array[], int n)
{
if (n <= 0)
return;
// 1) Create n empty buckets
Vector<Float>[] buckets = new Vector[n];
for (int i = 0; i < n; i++) {
buckets[i] = new Vector<Float>();
}
// 2) Put array elements in different buckets
for (int i = 0; i < n; i++) {
float idx = array[i] * n;
buckets[(int)idx].add(array[i]);
}
// 3) Sort individual buckets
for (int i = 0; i < n; i++) {
Collections.sort(buckets[i]);
}
// 4) Gather all buckets together into array[]
int arrayIndex = 0;
for (int i = 0; i < n; i++) {
int bucketSize = buckets[i].size();
for (int k = 0; k < bucketSize; k++) {
array[arrayIndex ++] = buckets[i].get(k);
}
}
}
// Driver code
public static void main(String args[])
{
float array[] = { (float)0.42, (float)0.32,
(float)0.35, (float)0.52,
(float)0.39, (float)0.47,
(float)0.50};
int n = array.length;
bucketSorting(array, n);
System.out.println("Sorted Array is: ");
for (float element : array) {
System.out.print(element + " ");
}
}
}
Input: [0.78, 0.17, 0.39, 0.26, 0.72, 0.94, 0.21, 0.12, 0.23, 0.68]
no. of buckets: 5
输出:
Sorted Array is: [0.12, 0.17, 0.21, 0.23, 0.26, 0.39, 0.68, 0.72, 0.78, 0.94]
注意:这适用于数组元素范围在0和1之间的情况。如果元素是整数怎么办?在这种情况下,我们将对每个存储桶的范围设置稍有不同,我们将在下一节中了解这一点。
下图显示了使用上述输入的代码的工作情况:
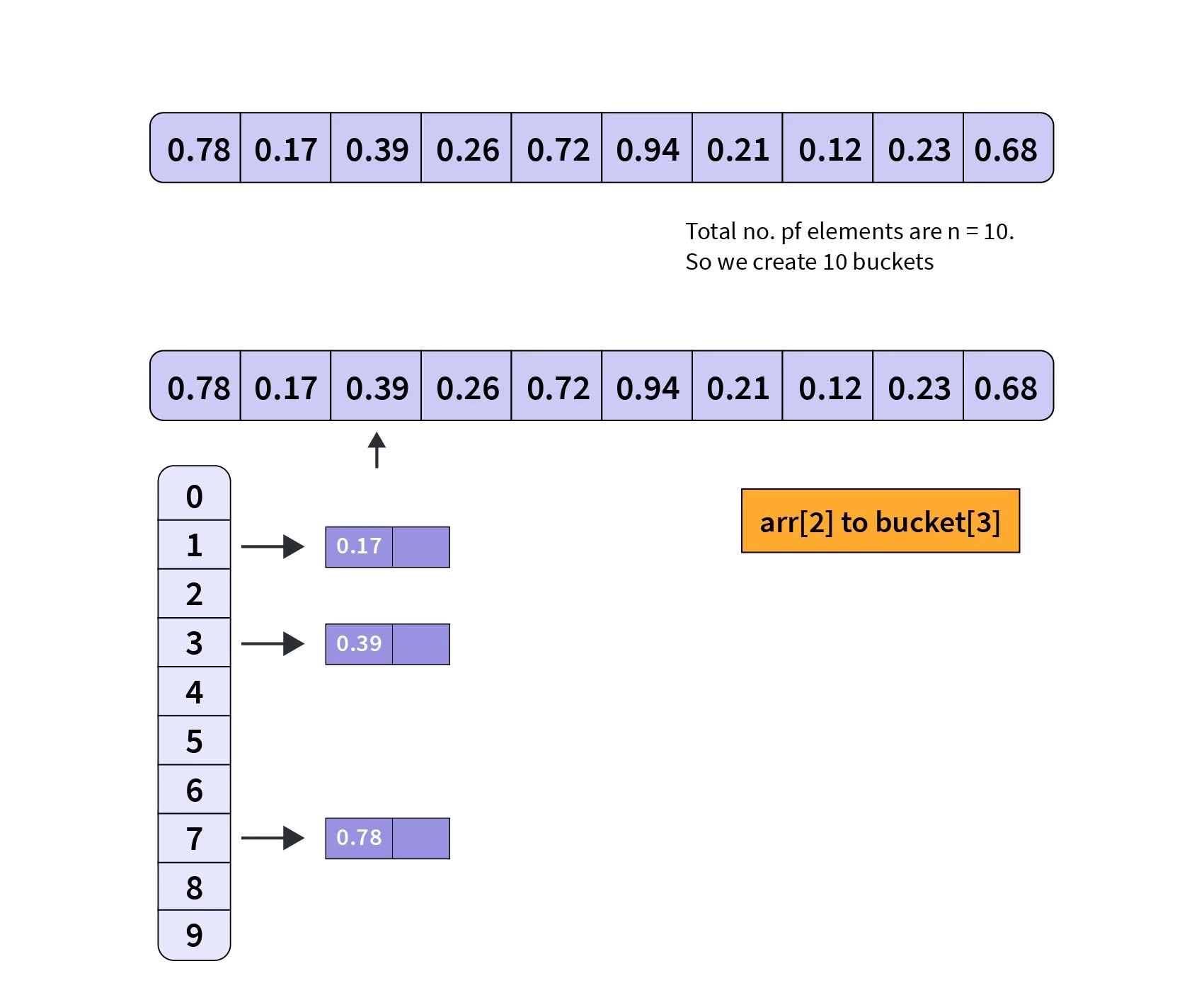
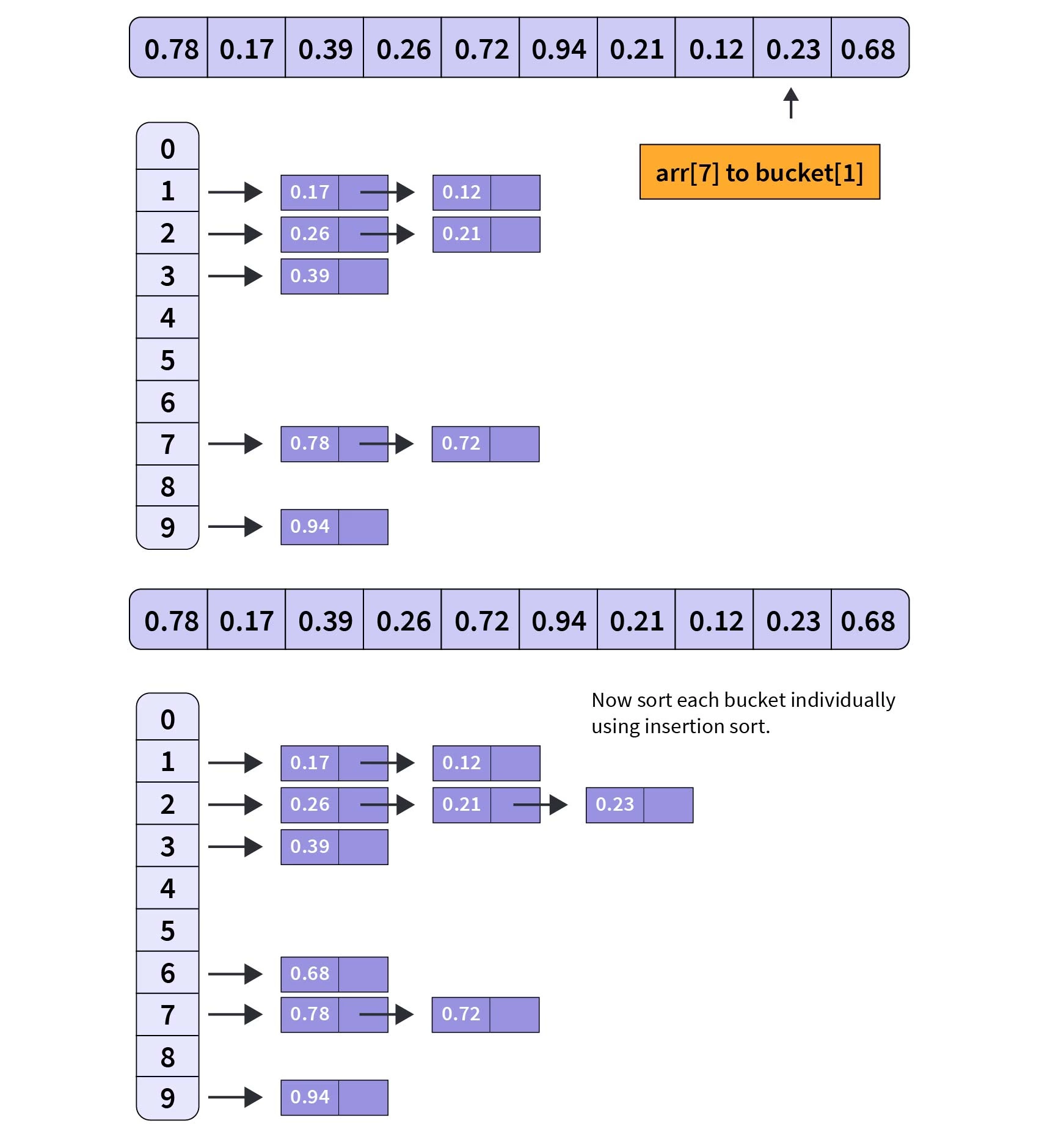
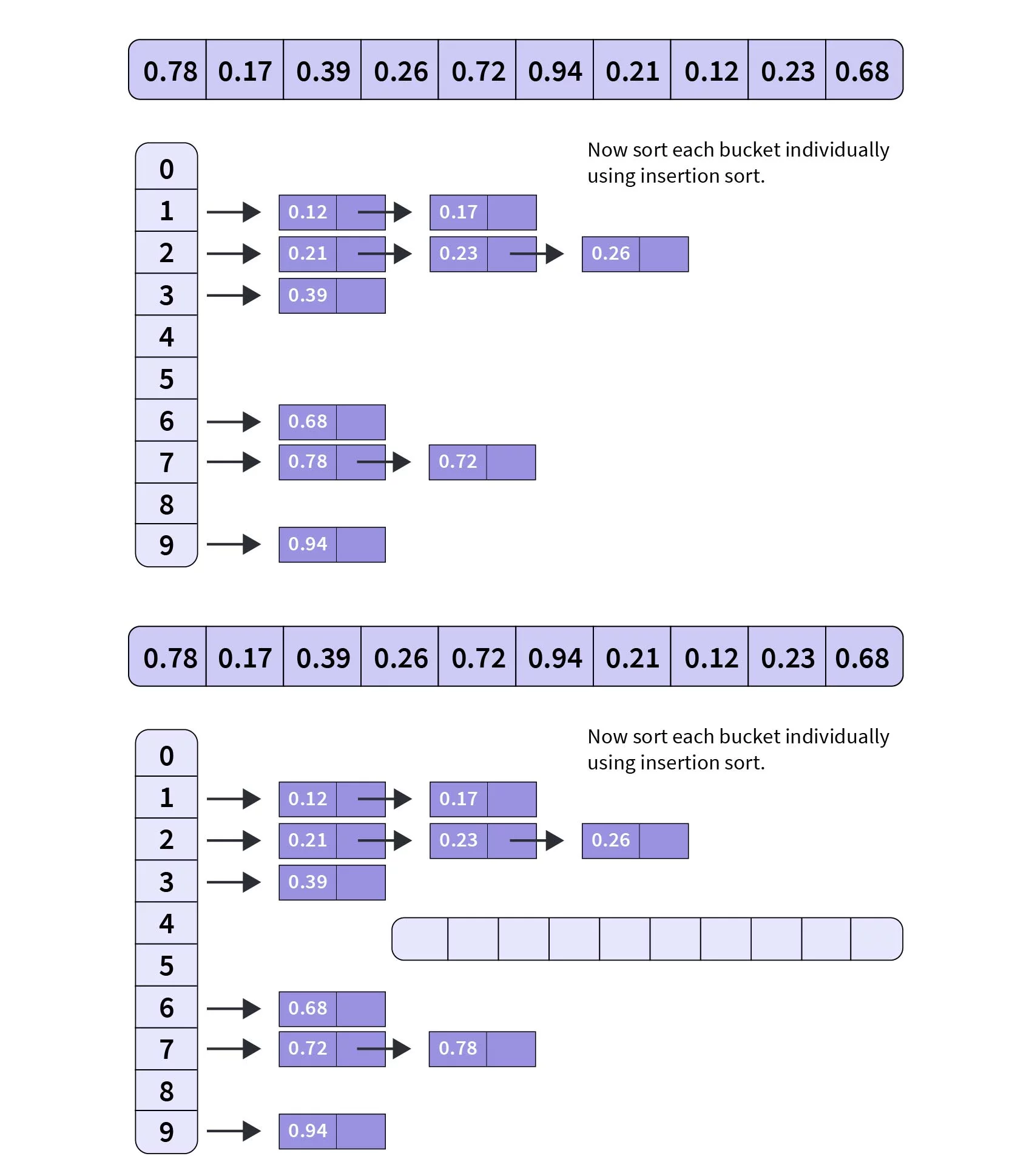
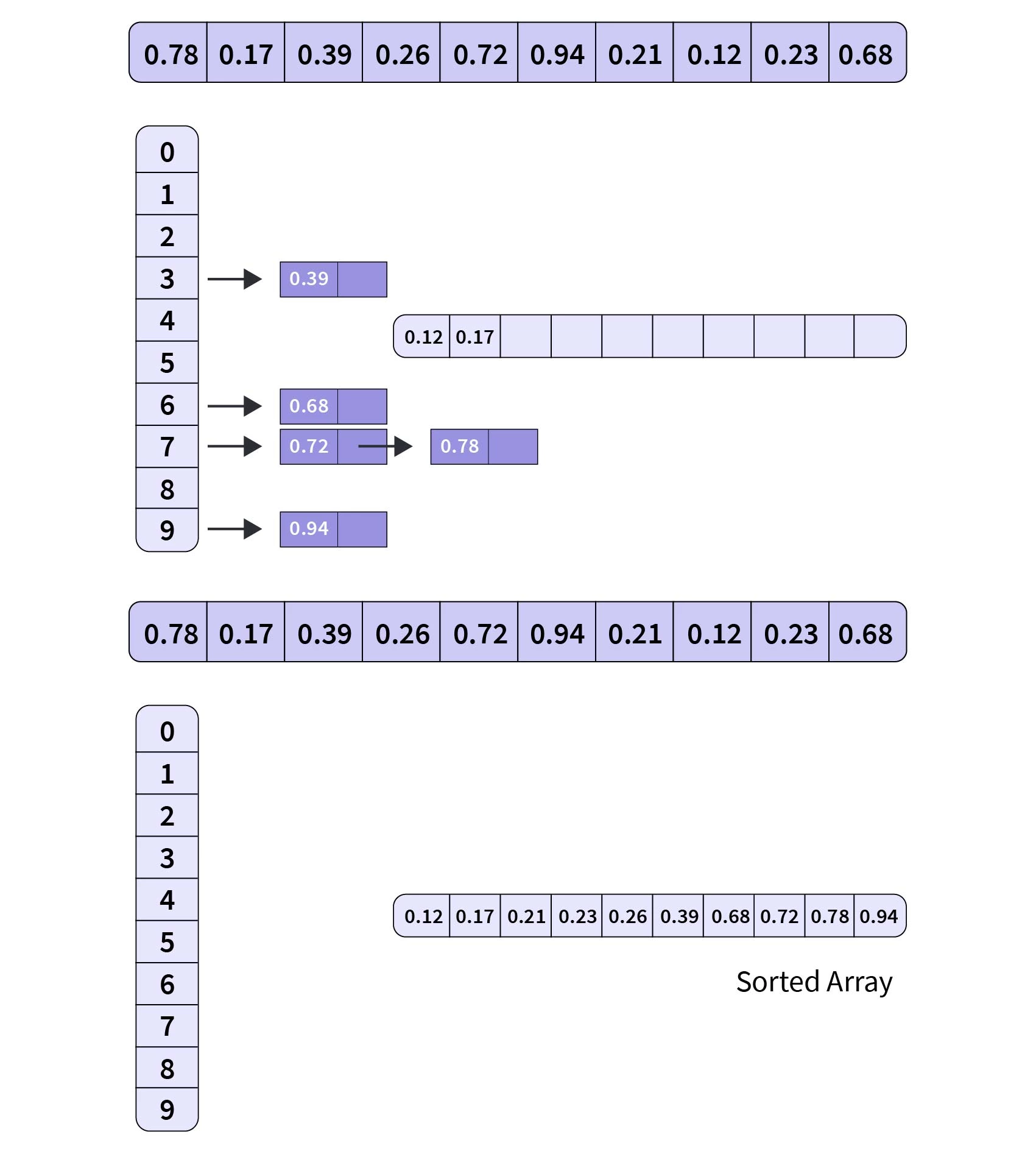
整数元素的桶排序
- 查找范围 = (最大 - 最小) / noOfBuckets
- BucketIndex = (数组[i] - 最小值) / 范围
- 最后整理并收集
对于整数元素,我们需要遵循以下算法:
- 计算数组的最大和最小元素
- 计算范围: range = (最大值 - 最小值) / n,其中 n 是桶的数量(作为参数给出)
- 创建n个空桶并初始化为0
- 循环遍历未排序的数组并执行以下操作: a) 计算bucketIndexbucketIndex = (array[i] - 最小值)/范围 b) 将数组的第i 个元素插入bucket[bucketIndex]
- 对各个桶进行排序
- 将所有元素聚集在一起
因此,我们有了排序后的数组。它是这样工作的:
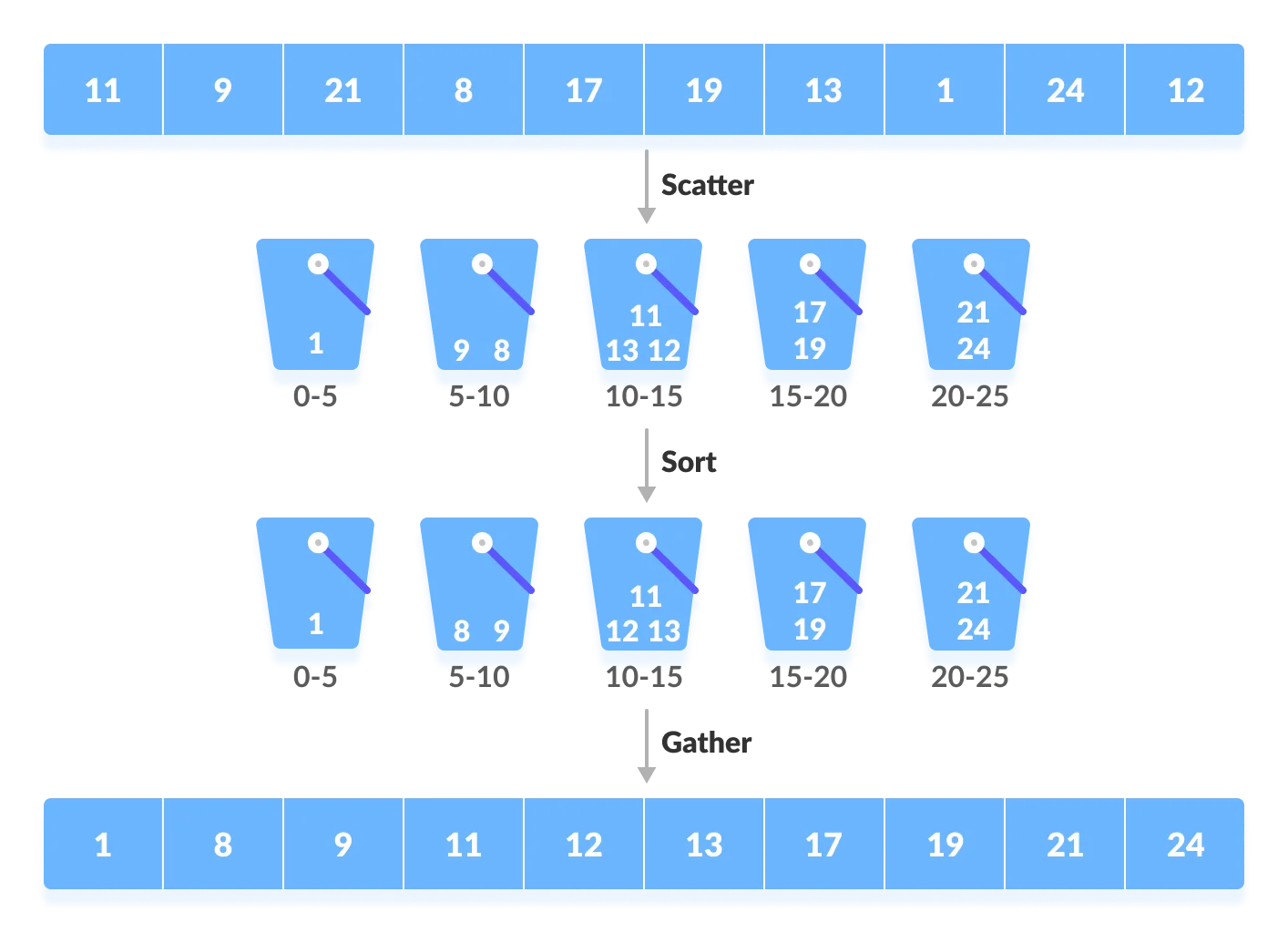
Python 代码 - 使用整数元素进行桶排序
# Python program for numbers having integer part
def bucketSorting(array, noOfBuckets):
maxElement = max(array)
minElement = min(array)
# Calculate Range
Range = (maxElement - minElement) / noOfBuckets
temp = []
# create n(noOfBuckets) empty buckets
for i in range(noOfBuckets):
temp.append([])
# Insert elments of array in corresponding buckets
for i in range(len(array)):
diff = (array[i] - minElement) / Range - int((array[i] - minElement) / Range)
if(diff == 0 and array[i] != minElement):
temp[int((array[i] - minElement) / Range) - 1].append(array[i])
else:
temp[int((array[i] - minElement) / Range)].append(array[i])
# Sort the buckets individually
for i in range(len(temp)):
if len(temp[i]) != 0:
temp[i].sort()
# Gather elements from all the buckets to get sorted array
k = 0
for lst in temp:
if lst:
for i in lst:
array[k] = i
k = k+1
# Driver Code
array = [11, 9, 21, 8, 17, 19, 13, 1, 24, 12]
noOfBuckets = 5
bucketSorting(array, noOfBuckets)
print("Sorted Array after Bucket Sorting is: ", array)
输出
Input: [11, 9, 21, 8, 17, 19, 13, 1, 24, 12]
no. of buckets: 5
Output:
Sorted Array after Bucket Sorting is:
1, 8, 9, 11, 12, 13, 17, 19, 21, 24
桶排序时间复杂度
- 最佳情况时间复杂度:O(n+k)
- 平均案例时间复杂度:O(n)
- 最坏情况时间复杂度:O(n^2^)
最佳情况时间复杂度:
如果数组元素均匀分布,则所有桶的桶大小几乎相同。因此,这将是占用最少时间的最佳情况。
如果每个存储桶内的所有元素都已排序,则排序时间复杂度将进一步降低。
要创建 n 个桶并分散数组中的每个元素,时间复杂度 = O(n)。如果我们使用插入排序对每个桶进行排序,时间复杂度 = O(k)。因此,桶排序的最佳情况时间复杂度 = O(n+k),其中 n = 元素数量, k = 桶数量
最坏情况时间复杂度
如果数组元素分布不均匀,即元素集中在特定范围内。
这将导致一个或多个存储桶比其他存储桶拥有更多元素,从而使存储桶排序像任何其他排序技术一样,其中每个元素都与另一个元素进行比较。如果数组中的元素以相反的顺序存在,时间复杂度会进一步增加。如果使用插入排序,最坏情况的时间复杂度可达 O(n^2^)。
桶排序空间复杂度
- 空间复杂度:O(n+k)
桶排序的空间复杂度为O(n+k),其中 n = 数组中元素的数量, k = 形成桶的数量 每个桶占用的空间为O(k),每个桶内有 n 个元素疏散。因此,空间复杂度变为O(n+k)。
应用领域
- 均匀分布的数据
- 范围0.0到 `1.0之间的浮点数
- 桶排序是一种非常不同类型的排序算法,因为它不涉及数字之间的直接比较。它只能应用于均匀分布的数据。
- 每当我们有0到1之间的浮点数时,桶排序可能是最好的排序方法。原因 - 如果我们使用合并排序、快速排序、堆排序等,问题将需要最小的O(nlogn)时间复杂度。另外,不能使用计数排序,因为浮点数不能用作索引。因此,桶排序最适合对浮点数范围[0.0-1.0]的数组进行排序。
结论
- 桶排序算法对数组的元素进行排序,首先将数组分成多个桶,对每个桶进行排序,然后将元素重新收集以形成排序后的数组。
- 桶排序用于对元素均匀分布或数组元素范围在0到1之间的数组进行排序。
- 桶排序可以表现出O(n+k)的最佳情况时间复杂度,其中n是桶的数量,k是桶的大小。
- 当数组元素是浮点数和整数时,提供桶范围的方式会有所不同。这在上面已详细讨论。

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容







所有评论(0)