堆排序

堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。首先简单了解下堆结构。

堆（数据结构）

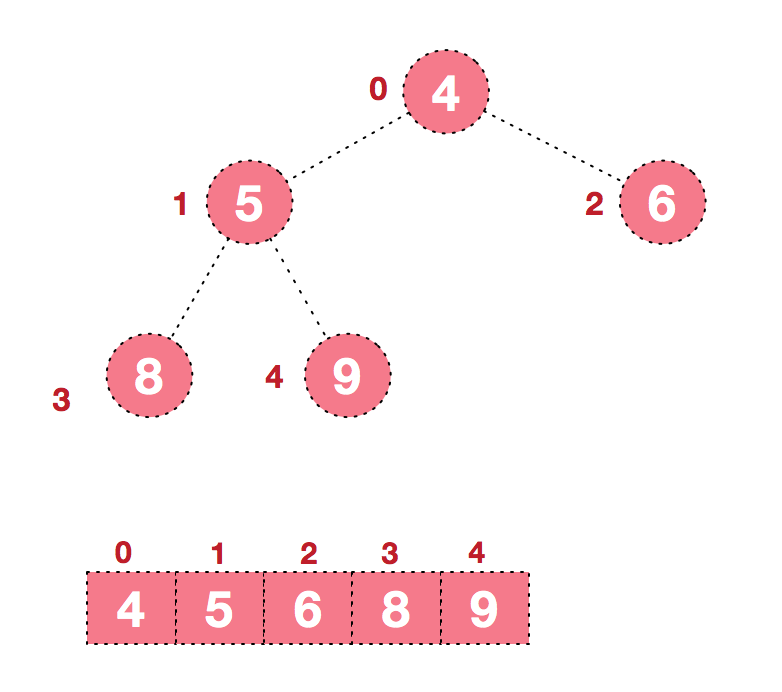
堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：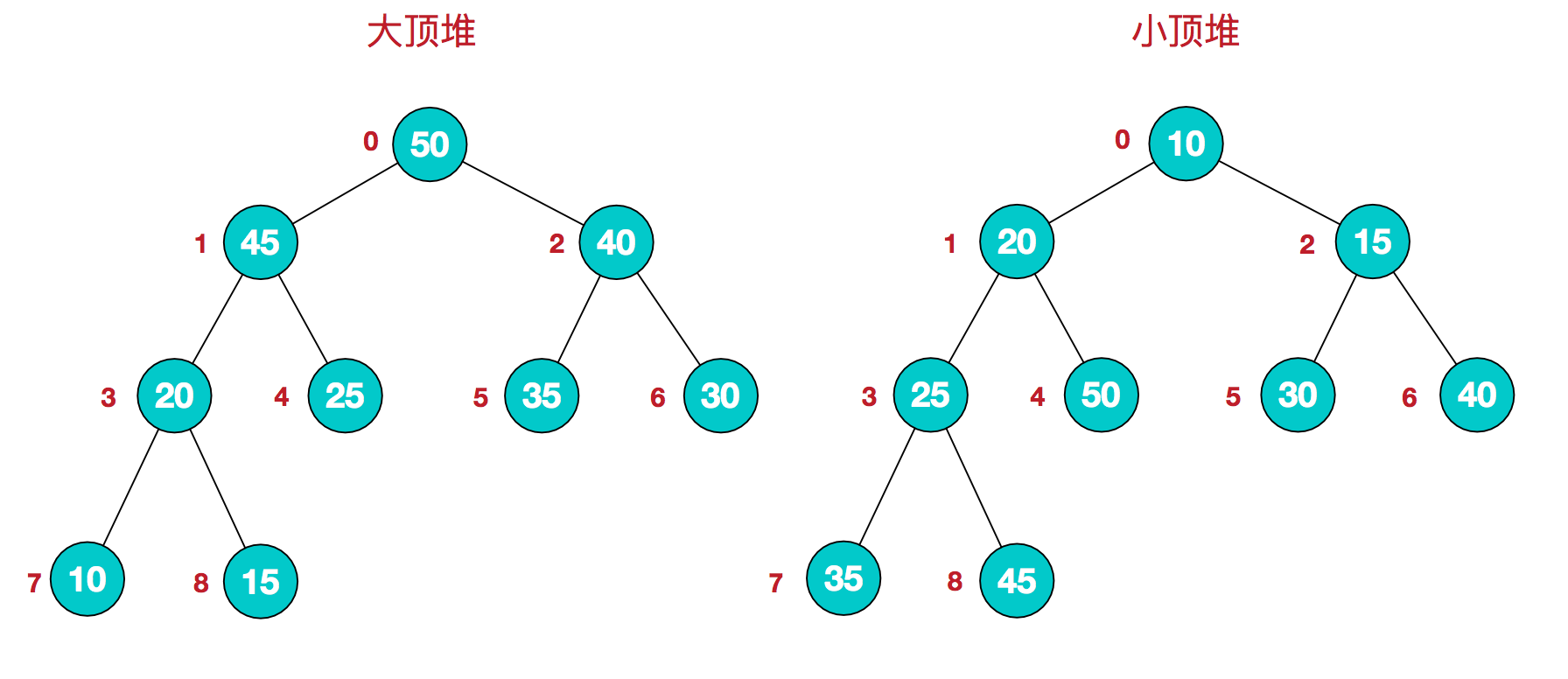

同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子

该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是：

• 大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
• 小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]

堆排序基本思想及步骤

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

堆排序具体过程说明：

步骤一： 构造初始堆。

将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

• 1.假设给定无序序列结构如下

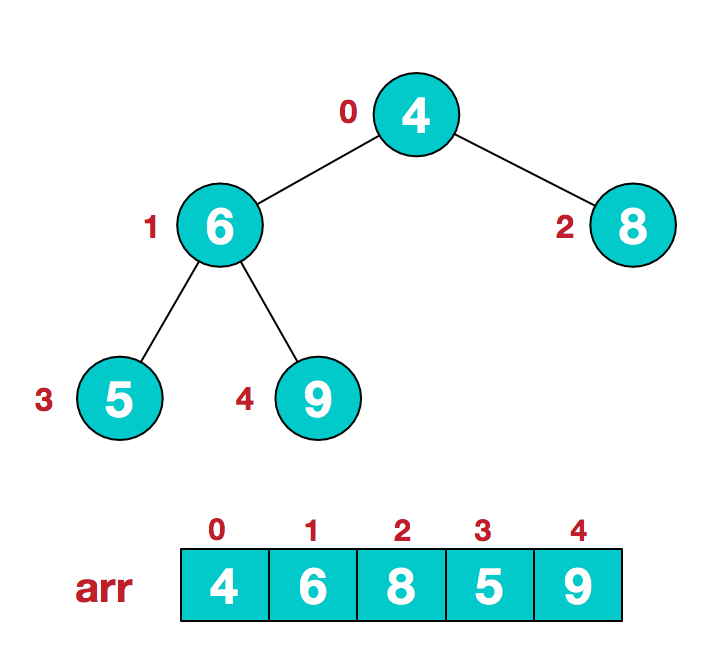
• 2.此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 n/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。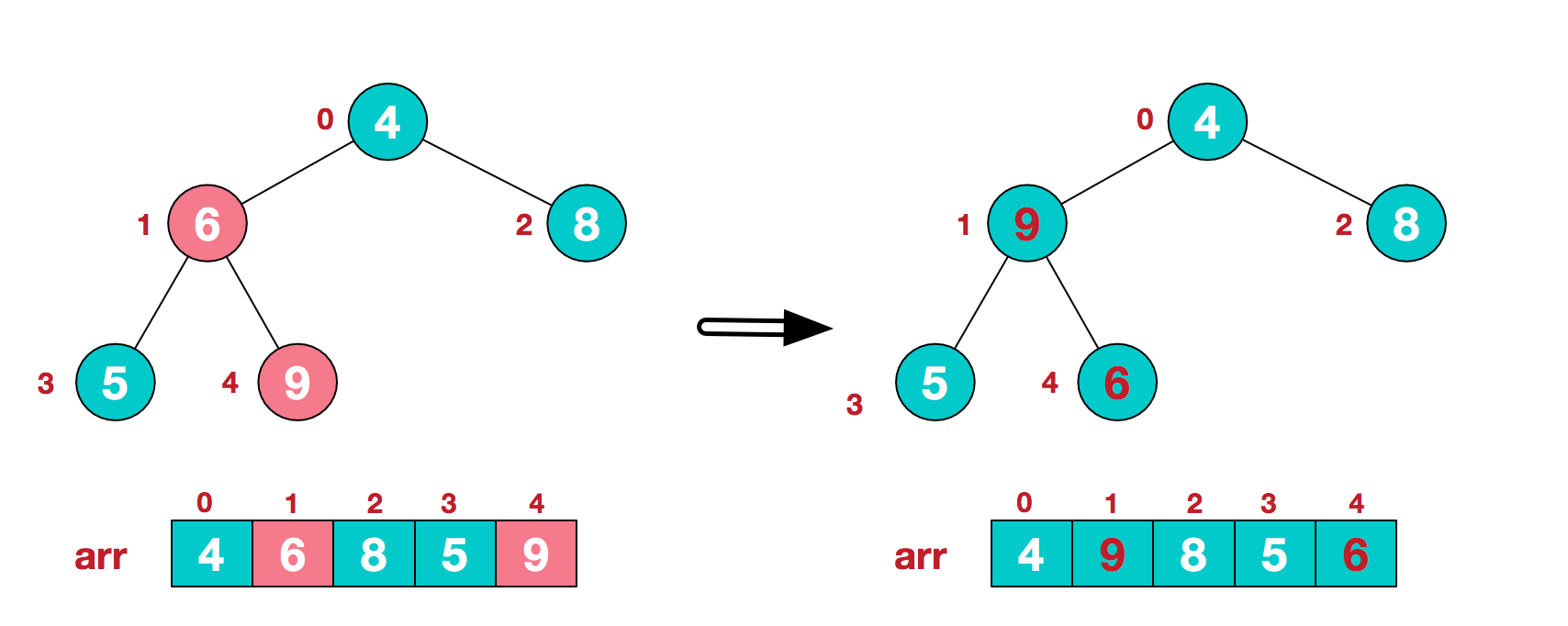
  
• 3.找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。
  
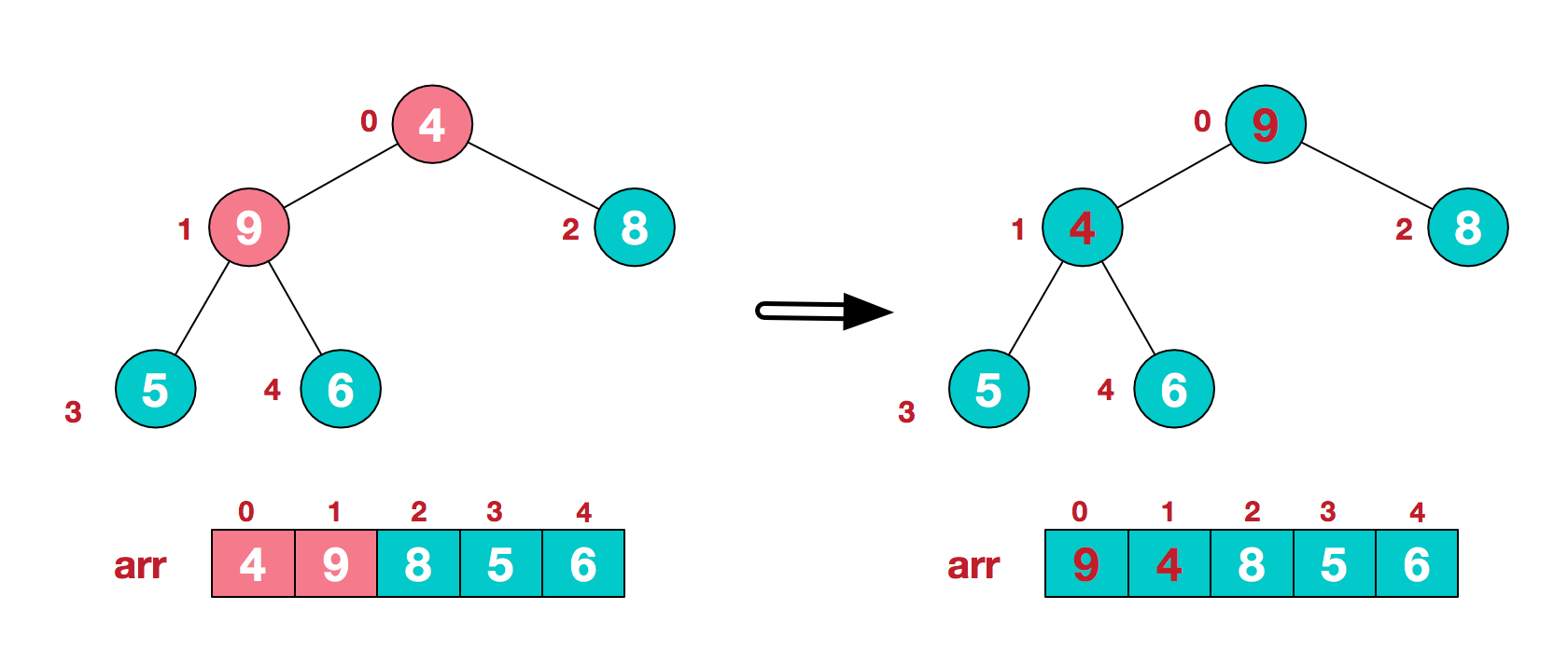
• 4.交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。
  
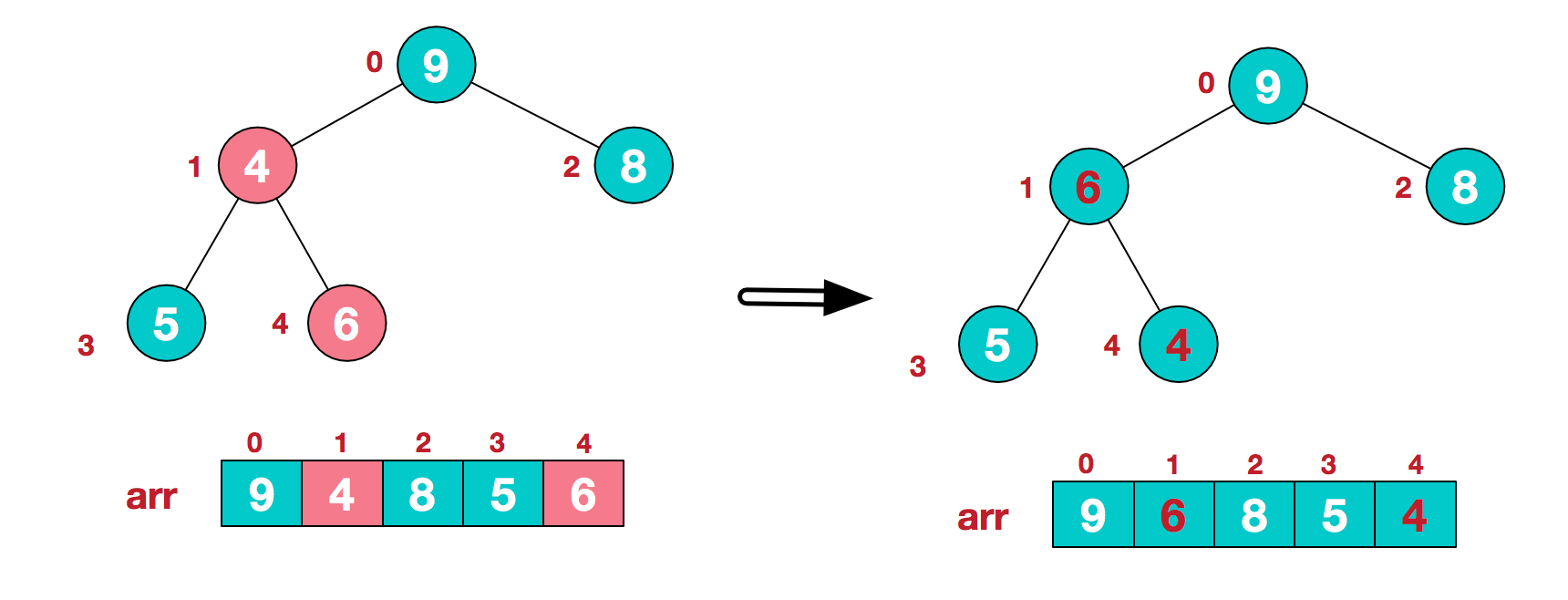
  此时，我们就将一个无需序列构造成了一个大顶堆

步骤二

将堆顶元素与末尾元素进行交换，使末尾元素最大。
然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

• a.将堆顶元素9和末尾元素4进行交换
  
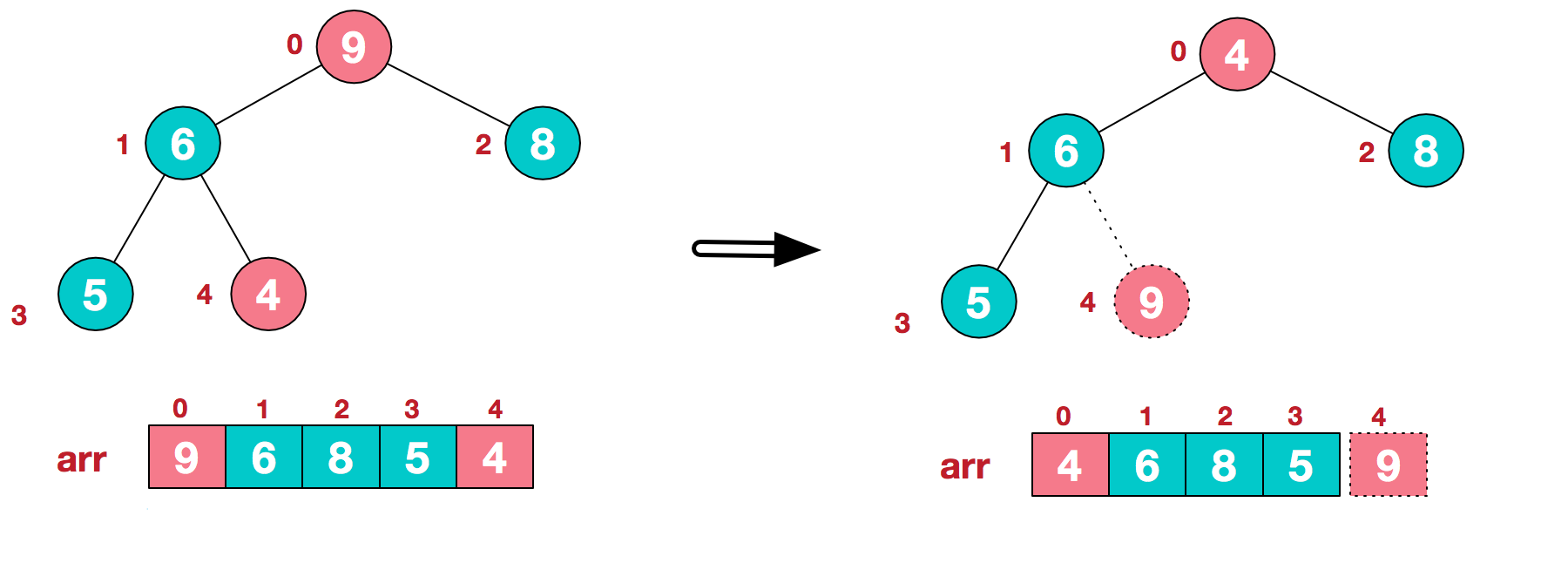
• b.重新调整结构，使其继续满足堆定义
  
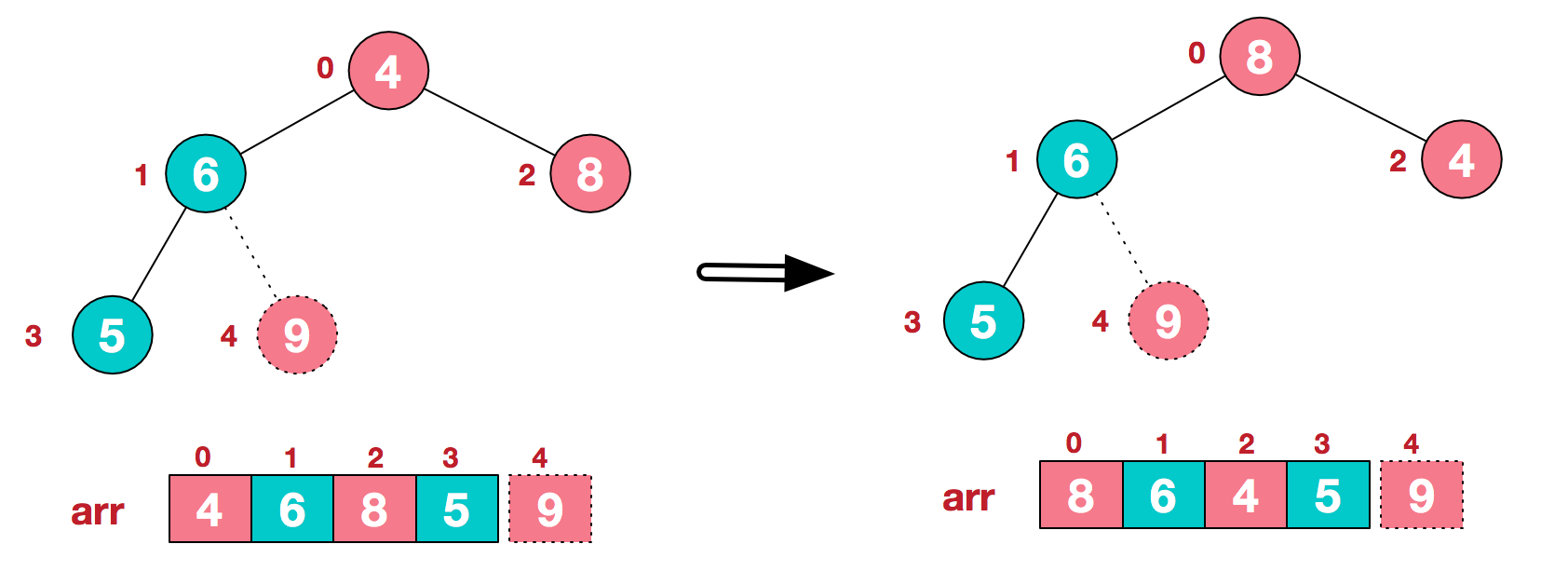
• c.再将堆顶元素8与末尾元素5进行交换，得到第二大元素8.
  
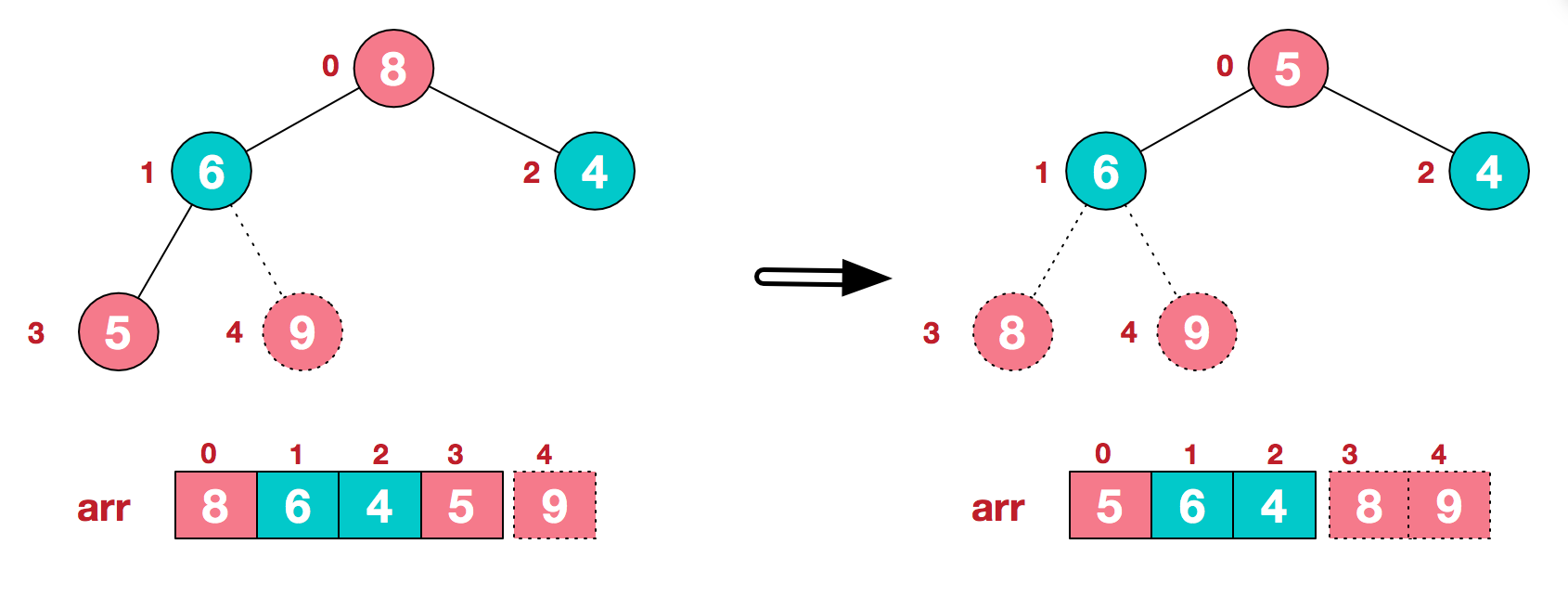
• d.后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序
  

再简单总结下堆排序的基本思路：

• a.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;
• b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;
• c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

代码实现：

/*
堆排序的基本思路：

　　a.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

　　b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

　　c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，
		反复执行调整+交换步骤，直到整个序列有序。
*/
#include <stdio.h>

void adjustHeap(int *data, int i, int length)
{
    int temp = data[i];//先取出当前元素i
    for(int k=i*2+1; k<length; k=k*2+1)
	{
		//从i结点的左子结点开始，也就是2i+1处开始
        if(k+1<length && data[k]<data[k+1])
		{
			//如果左子结点小于右子结点，k指向右子结点
            k++;
        }
        if(data[k] >temp)
		{
			//如果子节点大于父节点，将子节点值赋给父节点（不用进行交换）
            data[i] = data[k];
            i = k;
        }
		else{ break; }
    }
    data[i] = temp;//将temp值放到最终的位置
}

void heap_sort(int data[], int n)
{     
	int i;  int temp;
	 //1.构建大顶堆
    for (i=n/2-1; i>=0; i--)
    {
    	//从第一个非叶子结点从下至上，从右至左调整结构
    	adjustHeap(data,i,n); 
	}
		
    //2.调整堆结构+交换堆顶元素与末尾元素     
	for (i=n-1; i>=1; i--)
	{  
		//将堆顶元素与末尾元素进行交换
		temp = data[0];       	
		data[0] = data[i];  
		data[i] = temp;
		
		//重新对堆进行调整
		adjustHeap(data, 0, i);
	}
}


int main()
{
    int data[] = {8,3,6,2,4,5,7,1,9,0};
    
    printf("排序前的数据为：\n");
    for(int i=0; i<10;i++)
        printf("%d  ",data[i]);
    printf("\n\n");
    
    heap_sort(data,10);
    
    printf("排序后的结果为：\n");
    for(int i=0; i<10;i++)
        printf("%d  ",data[i]);
    printf("\n");
    
    return 0;
}

运行结果：

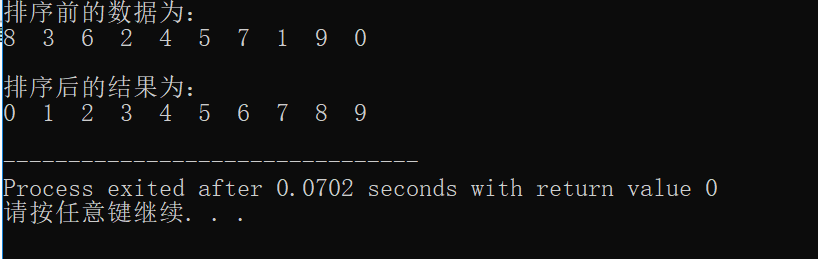
算法分析

堆排序是一种选择排序，整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆经推导复杂度为O(n)，在交换并重建堆的过程中，需交换n-1次，而重建堆的过程中，根据完全二叉树的性质，[log2(n-1),log2(n-2)…1]逐步递减，近似为nlogn。所以堆排序时间复杂度一般认为就是O(nlogn)级。

参考来源：https://www.cnblogs.com/chengxiao/p/6129630.html