树是数据结构的一种，它是由n（n>=1）个有限节点组成的一个具有层次关系的集合。

树具有的特点有：

（1）每个结点有零个或多个子结点

（2）没有父节点的结点称为根节点

（3）每一个非根结点有且只有一个父节点

（4）除了根结点外，每个子结点可以分为多个不相交的子树。

那么二叉树又有什么优势呢？

答：在实际使用时会根据链表和有序数组等数据结构的不同优势进行选择。有序数组的优势在于二分查找，链表的优势在于数据项的插入和数据项的删除。但是在有序数组中插入数据就会很慢，同样在链表中查找数据项效率就很低。综合以上情况，二叉树可以利用链表和有序数组的优势，同时可以合并有序数组和链表的优势，二叉树也是一种常用的数据结构。

二叉树的构成

二叉树由节点（node）和边组成。节点分为根节点、父节点、子节点。如下图所示：

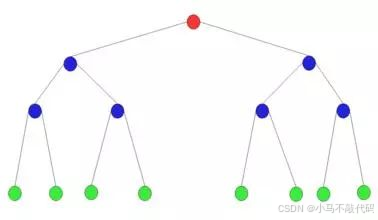
红色是根节点（root）。蓝色是子节点也是父节点，绿色的是子节点。其余的线是边。节点和链表中的节点一样都可以存放数据信息。树中的边可以用自引用表示，这种引用就是C/C++里面的指针。通常来说树是顶部小，底部大，且树呈分层结构。root节点时第0层，以此类推。二叉树最多有两个节点。

二叉树搜索

二叉搜索树的特点是一个节点左子节点的关键字小于这个父节点，右子节点关键字大于或等于这个父节点。

创建一个树节点

创建一个树节点包括左节点引用和右节点引用。

/**
* 创建一个树的节点
* 每个node存放两个数据
* 一个左node引用和一个右node引用
*/
public class Node {
  public  int iData;
  public double dData;
  public Node leftNode;
  public Node rightNode;
  //显示树节点信息
  public void showNode() {
      System.out.println("{ "+iData+","+dData+" }");
  }
}

创建一个树结构

创建一个树结构首先是向一个树中插入数据节点。当一棵树为null时，数据项是从树的root节点处开始插入，之后的插入顺序是根据搜索节点顺序规则进行插入。具体规则是：如果数据项比父节点的数据项要小，则插在父节点的左节点（leftNode），如果比父节点的数据项要大，则将新的node插入在父节点的右节点处（rightNode）。

private Node root;
//插入Node
//插入之前需要判断是否为null
//不为null需要比较大小直到currentNode为null就插入
public void insert(int iData,double dData ) {
  //创建node节点
  Node newNode=new Node();
  newNode.iData=iData;
  newNode.dData=dData;
  //判断root node是否为null
  if(root==null) {
      root=newNode;
  } else { //不为null
      Node current=root;
      Node parent;
      while(true) {
         parent=current;//保存当current变为null之前的那一个父节点
         if(iData<current.iData) { //插入左节点
             current=current.leftNode;//不断向左node寻找是否为null
             if(current==null) {
                 parent.leftNode=newNode;
                 return;
             }
         } else { //插入右节点
             current=current.rightNode;
             if(current==null) {
                 parent.rightNode=newNode;
                 return;
             }
         }
     }
  }
}

下图表示以上插入数据节点过程：

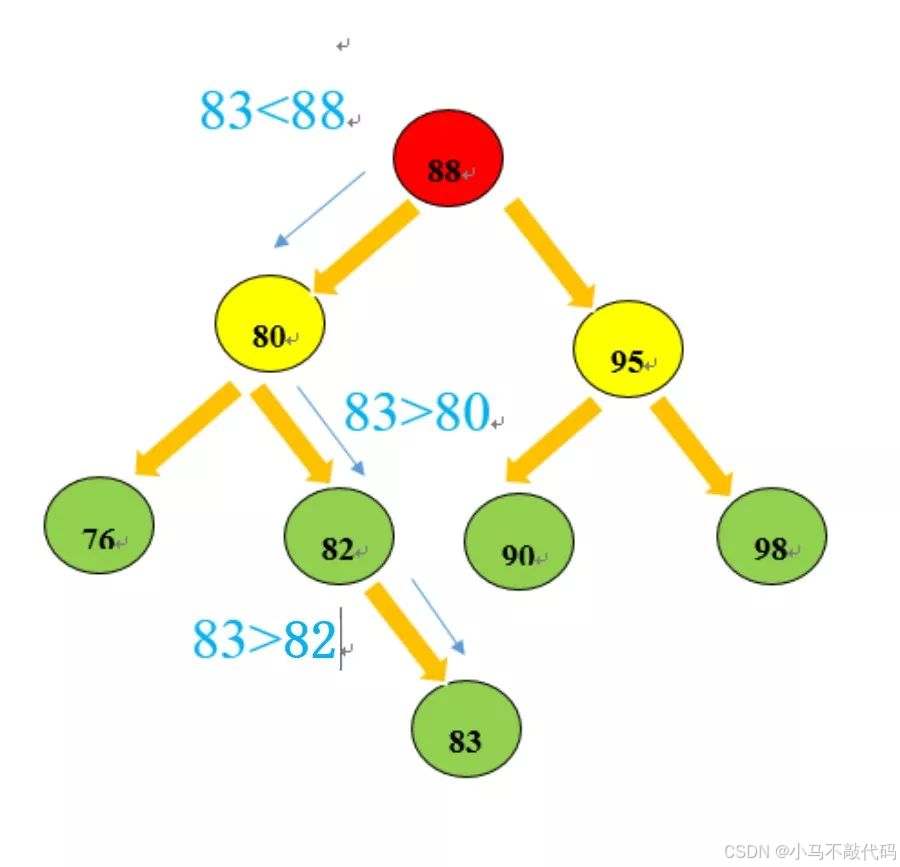
在插入节点的过程中其实也就是对tree遍历的过程，最终根据条件遍历到左右节点为null时进行添加新的节点。

查找关键字

查找关键字是数据结构一项重要操作项，在有序数组中通过二分排序效率非常高。在二叉树中的查找效率也比较高。因为二叉树的添加node的过程就是根据数据项的大小进行有序添加的，并不是毫无秩序的插入数据项。在有序的基础上进行查找关键字效率就会快很多。

//在tree中寻找关键字
//返回一个Node
//显示这个Node
public Node find(int key) {
      Node current=root;
      while(current.iData!=key) {
          if(current.iData>key)  {
              current=current.leftNode;
          }else  {
              current=current.rightNode;
          }
          if(current==null)
              return null;
      }
      return current;
}

树的最值查找

树的最值查找在树中查找是比较容易的，因为从root开始查找，最小值只会出现所有父节点的左节点处，同样最大值只会出现在所有父节点的沿着右节点搜索的最底层右节点处。

//查找树中的最大值和最小值
  //最小值存在于一棵树的最下层的最左node
  //最大值存在于一棵树的最下层的最右node
  public Node[] mVal() {
      Node minNode=null;
      Node maxNode=null;
      Node[] maxminVal=new Node[2];
      Node current=root;//从树的顶部开始搜索
      while(current!=null) {
          minNode=current;
          current=current.leftNode;  
      }
      maxminVal[0]=minNode;
      current=root;
      while(current!=null) {
          maxNode=current;
          current=current.rightNode;
      }
      maxminVal[1]=maxNode;
      return maxminVal;
  }

以上是通过node数组存放两个最值，这样避免写两个方法，最后返回一个node数组。

对上面树的操作进行测试：

Tree tree=new Tree();
tree.insert(3, 3.666);
tree.insert(1, 1.111);
tree.insert(2, 2.362);
tree.insert(4, 4.672);
tree.insert(5, 5.865);
tree.insert(6, 6.681);
Node node=tree.find(6);
if(node==null) {
   System.out.println("we can not find it");
}else {
   node.showNode();
}
//查找tree中的最值
Node[] temp=tree.mVal();
temp[0].showNode();
temp[1].showNode();

测试结果：

{ 6,6.681 }
{ 1,1.111 }
{ 6,6.681 }

由于第一个插入节点就是在root节点处进行插入，不管其数据项大小，该节点都是root节点，处于树的最顶层。

完全二叉树

简介 : 完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。

定义 : 若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

分析 : 一棵二叉树至多只有最下面的一层上的结点的度数可以小于2，并且最下层上的结点都集中在该层最左边的若干位置上，而在最后一层上，右边的若干结点缺失的二叉树，则此二叉树成为完全二叉树。

图示如下: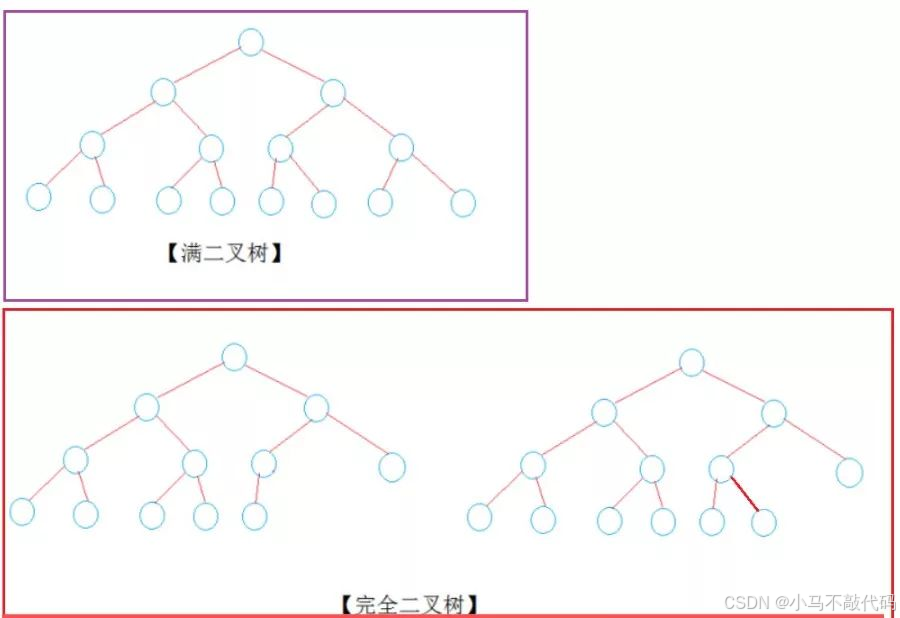

性质 :

如果一棵具有n个结点的深度为k的二叉树，它的每一个结点都与深度为k的满二叉树中编号为1~n的结点一一对应，这棵二叉树称为完全二叉树。

可以根据公式进行推导，假设n0是度为0的结点总数（即叶子结点数），n1是度为1的结点总数，n2是度为2的结点总数，则 ：

①n= n0+n1+n2 （其中n为完全二叉树的结点总数）；

又因为一个度为2的结点会有2个子结点，一个度为1的结点会有1个子结点，除根结点外其他结点都有父结点 :

②n= 1+n1+2n2 ；由①、②两式把n2消去得：n= 2n0+n1-1，由于完全二叉树中度为1的结点数只有两种可能0或1，由此得到n0=n/2 或 n0=(n+1)/2。

简便来算，就是 n0=n/2，其中n为奇数时（n1=0）向上取整；n为偶数时（n1=1）。可根据完全二叉树的结点总数计算出叶子结点数。

特点:

叶子结点只可能在最大的两层上出现,对任意结点，若其右分支下的子孙最大层次为L，则其左分支下的子孙的最大层次必为L 或 L+1；

出于简便起见,完全二叉树通常采用数组而不是链表存储,其存储结构如下:

var tree:array[1…n]of longint;{n:integer;n>=1}

对于tree[i]，有如下特点：

（1）若i为奇数且i>1，那么tree的左兄弟为tree[i-1]；

（2）若i为偶数且i<n，那么tree的右兄弟为tree[i+1]；

（3）若i>1，tree的父亲节点为tree[i div 2]；

（4）若2i<=n，那么tree的左孩子为tree[2i]；若2i+1<=n，那么tree的右孩子为tree[2i+1]；

（5）若i>n div 2,那么tree[i]为叶子结点（对应于（3））；

（6）若i<(n-1) div 2.那么tree[i]必有两个孩子（对应于（4））。

（7）满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

完全二叉树第i层至多有2^{（i-1）个节点，共i层的完全二叉树最多有2}i-1个节点。

完全二叉树的特点是：

1）只允许最后一层有空缺结点且空缺在右边，即叶子结点只能在层次最大的两层上出现；

2）对任一结点，如果其右子树的深度为j，则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个

完全二叉树判定

算法思路

判断一棵树是否是完全二叉树的思路

1>如果树为空，则直接返回错

2>如果树不为空：层序遍历二叉树

 2.1>如果一个结点左右孩子都不为空，则pop该节点，将其左右孩子入队列；

 2.1>如果遇到一个结点，左孩子为空，右孩子不为空，则该树一定不是完全二叉树；

 2.2>如果遇到一个结点，左孩子不为空，右孩子为空；或者左右孩子都为空；则该节点之后的队列中的结点都为叶子节点；该树才是完全二叉树，否则就不是完全二叉树；

代码实现:

/**
* 完全二叉树的判定
*/
public class CompleteTreeJudgment {
   //实现广度遍历需要的队列
   private LinkedList<Node> queue = new LinkedList<>();
   //第n层最左、右节点的标志
   private boolean most = false;

   public boolean processChild(Node child) {
       if (child != null) {
           if (!most) {
               queue.addLast(child);
           } else {
               return false;
           }
       } else {
           most = true;
       }
       return true;
   }

   public  boolean isCompleteTree (Node root) {
       //空数也是完全二叉树
       if (root == null) {
           return true;
       }
       //首先跟节点入队列
       queue.addLast(root);

       while (!queue.isEmpty()) {
           Node node = queue.removeFirst();

           //处理左子节点
           if (!processChild(node.left)) {
               return false;
           }
           //处理右子节点
           if (!processChild(node.right)) {
               return false;
           }
       }
       //广度优先遍历完毕，此树是完全二叉树
       return true;
   }
}

class Node {
   int data;
   Node left;
   Node right;
}