《数据结构》课程设计--c++多叉树
数据结构课程设计报告 c++实现多叉树及其可视化
树(多叉树)简单介绍
树(多叉树)是一种层次结构的数据结构,由节点组成,每个节点可以有多个子节点。树的最顶层节点称为根节点,没有子节点的节点称为叶子节点。
树的常见特点:
- 父节点:每个节点的直接上层节点。
- 子节点:每个节点的直接下层节点。
- 深度:从根节点到某节点的路径长度。
- 高度:从某节点到叶子节点的最长路径。
树在文件系统、组织结构图、数据库索引等场景广泛使用。常见操作包括遍历(前序、后序、层序遍历)和插入、删除节点等。
实验题目
多叉树设计(家谱)
实验内容
任务目标
在教材合适的代码基础上,实现关于树的存储、显示、操作等功能,并选用你熟悉的历史人物及其之间关系作为测试数据,国内国外、中文英文都可以,可以理解类似是建立一个简单的家谱管理系统。
任务描述
基本功能
- 1)自建测试数据,根结点是你自己的名字,初始树的高度至少为4,结点数量至少为10,每个结点的值不要重复;(10分)
- 2)系统提供菜单,显示以及可以选择相应的功能;(8分)
- 3)初始树的数据从文件载入,文件格式自定;(10分)
- 4)按树的显示方式显示树,同时显示其高度、结点数;(12分)
- 5)新增结点功能,操作逻辑自行实现;(10分)
- 6)删除结点功能,操作逻辑自行实现;(10分)
- 7)修改结点功能,操作逻辑自行实现;(10分)
- 8)树被修改后,也就是经过上述三种操作后,立即重新显示;(9分)
- 9)给出先根、后根以及层序遍历的三种顺序;(9分)
- 10)系统退出后,修改的数据自动存储到文件。(12分)
进阶功能
- 1)图形界面显示树;(10分)
- 2)动画方式实现遍历过程。(15分)
本文实现全部功能,难点&创新点:
- 1)动画实现三种遍历顺序,树形或文字的展示;
- 2)树形展示,具有颜色的cmd界面,清晰直观;
- 3)从文件输入随意信息即可建立初始树;
- 4)插入结点时,若已存在相同节点名,则将两者相关联,且子结点不可能通过操作成为其父节点的父节点,具有一定的现实意义,健壮性高。
解决方案
算法设计总述
在本实验中使用C++语言,实现了多叉树的各种操作。整体思路包括通过节点类 TreeNode 定义了多叉树的节点结构,包括数据元素和子节点列表。通过 MultiTree 类定义了多叉树的操作,包括获取根节点、从文件读取创建树、以先根、后根或层序遍历方式输出树的结果至文件、查找父节点、查找兄弟节点、查找子节点、插入节点、删除节点及子树、计算树的高度、计算节点数、查找特定节点、找到节点所在层次、移动和替换节点、动画演示输出等功能。在代码中还强调了错误处理和异常情况的处理,对文件的读取和写入进行了充分的检查和处理,以确保程序的稳定性和可靠性。
类和结构体 的数据成员设计
class TreeNode { //树的节点类
public:
string data;
vector<TreeNode*> children; //为符合多叉树一个父节点可能会有多个孩子节点的情况
TreeNode(string val){
data = val;
}
void addChild(TreeNode* child){ //通过指针实现增加孩子(子树一并移动)
children.push_back(child);
}
};
class MultiTree {
public:
TreeNode* root;// 成员变量
MultiTree(){ //构造函数
root = nullptr;
}
MultiTree(const string& e){
root = new TreeNode(e);
}
TreeNode* getRoot(){ // 获取根节点
return root;
}
///////////////其他函数见下表
};
此外,为了更好的显示二叉树,设计了一个SetColor函数,更清晰美观的展示输出内容。
SetColor函数设计
void SetColor(int fore = 7, int back = 0) {// 改变控制台中输出的颜色
unsigned char m_color = fore;
m_color += (back << 4);
SetConsoleTextAttribute(GetStdHandle(STD_OUTPUT_HANDLE), m_color);
return;
}
MultiTree类中的函数设计
#ifndef __MULTTREE_H__
#define __MULTTREE_H__
#include <iostream>
#include <vector>
#include <string>
#include <queue>
#include <utility>
#include <fstream>
#include <iomanip>
#include <algorithm>
#include <chrono> // 用于时间延迟
#include <thread> // 用于时间延迟
#include "SetColor.h"
using namespace std;
class TreeNode {
public:
string data;
vector<TreeNode*> children;
TreeNode(string val)
{
data = val;
}
void addChild(TreeNode* child)
{
children.push_back(child);
}
};
class MultiTree {
public:
// 成员变量
TreeNode* root;
//构造函数
MultiTree()
{
root = nullptr;
}
MultiTree(const string& e)
{
root = new TreeNode(e);
}
// 获取根节点
TreeNode* getRoot()
{
return root;
}
// 从文件读取
void createTreeFromFile(const string& filename)
{
ifstream inputFile(filename);
string line;
while (getline(inputFile, line)) {
istringstream iss(line);
string nodeName;
string parentNodeName;
iss >> nodeName >> parentNodeName;
if (parentNodeName == "NULL") {
insertChild(nullptr, nodeName);
} else {
TreeNode* parentNode = findNode(root, parentNodeName); // 实现 findNode
insertChild(parentNode, nodeName);
}
}
}
// 将先根遍历结果输出到给定的文件输出流
void preOrderTraversal(TreeNode* root, ofstream& outputFile)
{
if (root == nullptr)
{
return;
}
outputFile << root->data << " ";
for (TreeNode* child : root->children)
{
preOrderTraversal(child, outputFile);
}
}
// 将后根遍历结果输出到给定的文件输出流
void postOrderTraversal(TreeNode* root, ofstream& outputFile)
{
if (root == nullptr)
{
return;
}
for (TreeNode* child : root->children)
{
postOrderTraversal(child, outputFile);
}
outputFile << root->data << " ";
}
// 保存到文件
void saveMultiTreeToFile(TreeNode* root, const string& filename)
{
ofstream outputFile(filename);
if (outputFile.is_open())
{
// 输出树的先序遍历结果到文件
outputFile << "先根遍历结果: ";
preOrderTraversal(root, outputFile);
outputFile << endl;
// 输出树的中序遍历结果到文件
outputFile << "后根遍历结果: ";
postOrderTraversal(root, outputFile);
outputFile << endl;
outputFile.close();
SetColor(3, 0);
cout << "多叉树已成功写入到文件: " << filename << endl;
SetColor();
}
else
{
SetColor(3, 0);
cout << "无法打开文件:" << filename << ",树写入失败" << endl;
SetColor();
}
}
// 找到父节点
TreeNode* findParentNode(TreeNode* node, const string& value, TreeNode* parent = nullptr)
{
if (node == nullptr) {
return nullptr;
}
if (node->data == value) {
return parent;
}
for (auto child : node->children) {
TreeNode* result = findParentNode(child, value, node);
if (result != nullptr) {
return result;
}
}
return nullptr;
}
// 找兄弟节点
vector<TreeNode*> findBrotherNodes(TreeNode* root, const string& value)
{
TreeNode* parent = findParentNode(root, value);
vector<TreeNode*> brothers;
if (parent != nullptr)
{
for (auto child : parent->children)
{
if (child->data != value)
{
brothers.push_back(child);
}
}
}
return brothers;
}
vector<TreeNode*> findChildrenNodes(TreeNode* node)
{
vector<TreeNode*> childrenList;
if (node == nullptr)
{
return childrenList;
}
for (auto child : node->children)
{
childrenList.push_back(child);
}
return childrenList;
}
// 插入一个节点作为上一个节点的子节点
void insertChild(TreeNode* parent, const string& value)
{
if (parent == nullptr)
{
root = new TreeNode(value);
}
else
{
TreeNode* newChild = new TreeNode(value);
parent->children.push_back(newChild);
}
}
// 删除结点
void deleteSubtree(TreeNode* node)
{
if (node == nullptr)
{
return;
}
for (auto child : node->children)
{
deleteSubtree(child); // 递归删除子节点
}
delete node; // 删除当前节点
}
bool deleteNodeAndSubtree(TreeNode* root, const string& value)
{
if (root == nullptr)
{
return false;
}
if (root->data == value)
{
deleteSubtree(root); // 删除当前节点及其所有子节点
return true;
}
// 在当前节点的子节点中递归查找
for (size_t i = 0; i < root->children.size(); i++)
{
if (root->children[i]->data == value)
{
deleteSubtree(root->children[i]); // 删除子树
root->children.erase(root->children.begin() + i); // 移除当前子节点
return true;
}
}
// 如果在子节点中没有找到,继续向下搜索
for (size_t i = 0; i < root->children.size(); i++)
{
if (deleteNodeAndSubtree(root->children[i], value))
{
return true; // 如果子树中已完成删除操作,返回true
}
}
return false;
}
// 计算树(结点的子树)的高度
int calculateHeight(TreeNode* node)
{
if (node == nullptr) {
return 0;
}
int maxHeight = 0;
for (auto child : node->children) {
maxHeight = max(maxHeight, calculateHeight(child));
}
return maxHeight + 1;
}
// 计算节点数
int calculateNodeCount(TreeNode* node)
{
if (node == nullptr) {
return 0;
}
int count = 1;
for (auto child : node->children) {
count += calculateNodeCount(child);
}
return count;
}
// 找到结点
TreeNode* findNode(TreeNode* current, const std::string& nodeName)
{
if (current == nullptr)
{
return nullptr;
}
if (current->data == nodeName)
{
return current;
}
for (TreeNode* child : current->children)
{
TreeNode* found = findNode(child, nodeName);
if (found != nullptr)
{
return found;
}
}
return nullptr;
}
// 在第几层
int findNodeLevel(TreeNode* root, const string& value)
{
if (root == nullptr)
{
return -1; // 树为空,返回-1
}
queue<pair<TreeNode*, int>> nodesQueue;
nodesQueue.push(make_pair(root, 1)); // 将根节点加入队列
while (!nodesQueue.empty())
{
TreeNode* current = nodesQueue.front().first;
int level = nodesQueue.front().second;
nodesQueue.pop();
if (current->data == value)
{
return level;
}
// 遍历当前节点的每个子节点,将它们加入队列并设置正确的层级
for (TreeNode* child : current->children)
{
nodesQueue.push(make_pair(child, level + 1));
}
}
return -1; // 未找到节点,返回-1
}
// 移动结点
bool moveAndReplaceNode(TreeNode* root, const string& targetValue, const string& destinationValue)
{
int targetLevel = findNodeLevel(root, targetValue);
int destinationLevel = findNodeLevel(root, destinationValue);
if (targetLevel < 0 || destinationLevel < 0)
{// 错误处理:如果目标值或者目标位置不存在,返回 false
return false;
}
if (targetLevel < destinationLevel)
{// 错误处理:如果目标值在目标位置之下,无法移动,返回 false
return false;
}
TreeNode* targetParent = findParentNode(root, targetValue);
TreeNode* destinationParent = findParentNode(root, destinationValue);
if (targetParent == nullptr || destinationParent == nullptr)
{// 错误处理:如果找不到目标值或者目标位置的父节点,返回 false
return false;
}
// 寻找目标值在其父节点中的位置,然后移除
for (size_t i = 0; i < targetParent->children.size(); i++)
{
if (targetParent->children[i]->data == targetValue)
{
TreeNode* toMove = targetParent->children[i];
targetParent->children.erase(targetParent->children.begin() + i);
// 将目标值移动到目标位置的子节点中
destinationParent->children.push_back(toMove);
return true; // 移动成功
}
}
return false; // 未能成功移动
}
// 动画演示输出顺序
void printaniMultiTree(TreeNode* root, TreeNode* cur, string prefix = "", bool isLast = true)
{
if (root) {
SetColor(6, 0);
cout << prefix;
SetColor();
SetColor(6, 0);
if(root->data!="(朱俊枫)")
{
cout << (isLast ? "└───" : "├───");
}
SetColor();
if(root==cur)
{
SetColor(0, 5);
cout << root->data ;
SetColor();
cout << endl;
}
else if(root->data=="(朱俊枫)")
{
SetColor(0, 6);
cout << root->data ;
SetColor();
cout << endl;
}
else if(root->data!="(朱俊枫)")
{
SetColor(2, 0);
cout << root->data << endl;
SetColor();
}
for (size_t i = 0; i < root->children.size(); ++i)
{
if(i == root->children.size() - 1)
{
printaniMultiTree(root->children[i], cur, prefix + (isLast ? " " : "│ "), true);
}
else
{
printaniMultiTree(root->children[i], cur, prefix + (isLast ? " " : "│ "), false);
}
}
}
}
void preOrderprint(TreeNode* node)
{
if (node == nullptr)
{
return;
}
TreeNode *current = node;
SetColor(3, 0);
cout << "先根遍历结果: ";
SetColor();
preOrderTraversal(root, current);
cout << endl;
printaniMultiTree(root, current);
Sleep(1000);
system("cls");
for (TreeNode* child : node->children) {
preOrderprint(child); // 递归处理每个子节点
}
}
void postOrderprint(TreeNode* node)
{
if (node == nullptr)
{
return;
}
TreeNode *current = node;
for (TreeNode* child : node->children)
{
postOrderprint(child); // 递归处理每个子节点
}
SetColor(3, 0);
cout << "后根遍历结果: ";
SetColor();
postOrderTraversal(root, current);
cout << endl;
printaniMultiTree(root, current);
Sleep(1000);
system("cls");
}
void levelOrderprint(TreeNode* root)
{
if (root == nullptr)
{
return;
}
queue<TreeNode*> nodesQueue;
nodesQueue.push(root);
while (!nodesQueue.empty())
{
TreeNode* current = nodesQueue.front();
SetColor(3, 0);
cout << "层序遍历结果: ";
SetColor();
levelOrderTraversal(root, current);
cout << endl;
printaniMultiTree(root, current);
Sleep(1000);
system("cls");
nodesQueue.pop();
for (TreeNode* child : current->children)
{
nodesQueue.push(child); // 将子节点加入队列
}
}
}
// 先根遍历(前序遍历)
void preOrderTraversal(TreeNode* root, TreeNode* cur)
{
if (root == nullptr)
{
return;
}
if(root==cur)
{
SetColor(0, 5);
cout << root->data << " ";
SetColor();
}
else
{
cout << root->data << " "; // 处理当前节点
}
for (TreeNode* child : root->children) {
preOrderTraversal(child, cur); // 递归处理每个子节点
}
}
// 后根遍历(后序遍历)
void postOrderTraversal(TreeNode* root, TreeNode* cur)
{
if (root == nullptr)
{
return;
}
for (TreeNode* child : root->children)
{
postOrderTraversal(child, cur); // 递归处理每个子节点
}
if(root==cur)
{
SetColor(0, 5);
cout << root->data << " ";
SetColor();
}
else
{
cout << root->data << " "; // 处理当前节点
}
}
// 层序遍历
void levelOrderTraversal(TreeNode* root, TreeNode* cur)
{
if (root == nullptr)
{
return;
}
queue<TreeNode*> nodesQueue;
nodesQueue.push(root);
while (!nodesQueue.empty())
{
TreeNode* current = nodesQueue.front();
nodesQueue.pop();
if(current==cur)
{
SetColor(0, 5);
cout << current->data << " ";
SetColor();
}
else
{
cout << current->data << " "; // 处理当前节点
}
for (TreeNode* child : current->children)
{
nodesQueue.push(child); // 将子节点加入队列
}
}
}
void animateTraversal(TreeNode* root) {
if (root == nullptr) {
return;
}
// 显示先根遍历动画
SetColor(3, 0);
cout << "先根遍历" << endl;
SetColor();
animatedPreOrderTraversal(root);
cout << endl;
// 显示后根遍历动画
SetColor(3, 0);
cout << "后根遍历" << endl;
SetColor();
animatedPostOrderTraversal(root);
cout << endl;
// 显示层序遍历动画
SetColor(3, 0);
cout << "层序遍历" << endl;
SetColor();
animatedLevelOrderTraversal(root);
cout << endl;
}
void animatedPreOrderTraversal(TreeNode* root) {
if (root == nullptr) {
return;
}
cout << root->data << " "; // 处理当前节点
this_thread::sleep_for(chrono::milliseconds(70)); // 添加延迟
for (TreeNode* child : root->children) {
animatedPreOrderTraversal(child); // 递归处理每个子节点
}
}
void animatedPostOrderTraversal(TreeNode* root) {
if (root == nullptr) {
return;
}
for (TreeNode* child : root->children) {
animatedPostOrderTraversal(child); // 递归处理每个子节点
}
this_thread::sleep_for(chrono::milliseconds(70)); // 添加延迟
cout << root->data << " "; // 处理当前节点
}
void animatedLevelOrderTraversal(TreeNode* root) {
if (root == nullptr) {
return;
}
queue<TreeNode*> nodesQueue;
nodesQueue.push(root);
while (!nodesQueue.empty()) {
TreeNode* current = nodesQueue.front();
nodesQueue.pop();
cout << current->data << " "; // 处理当前节点
this_thread::sleep_for(chrono::milliseconds(70)); // 添加延迟
for (TreeNode* child : current->children) {
nodesQueue.push(child); // 将子节点加入队列
}
}
}
// 树形输出
void printMultiTree(TreeNode* root, string prefix = "", bool isLast = true)
{
if (root) {
SetColor(6, 0);
cout << prefix;
SetColor();
SetColor(6, 0);
if(root->data!="(朱俊枫)")
{
cout << (isLast ? "└───" : "├───");
}
SetColor();
if(root->data=="(朱俊枫)")
{
SetColor(0, 6);
cout << root->data ;
SetColor();
cout << endl;
}
if(root->data!="(朱俊枫)")
{
SetColor(2, 0);
cout << root->data << endl;
SetColor();
}
// 添加了对root->children是否为空的检查
for (size_t i = 0; i < root->children.size(); ++i)
{
// 添加了对i是否越界的检查
if(i == root->children.size() - 1)
{
printMultiTree(root->children[i], prefix + (isLast ? " " : "│ "), true);
}
else
{
printMultiTree(root->children[i], prefix + (isLast ? " " : "│ "), false);
}
}
}
}
// 输出模板
void coutmodel()
{
SetColor(8, 0);
cout << "《红楼梦》贾家人物关系表 (左根右子)" << endl << endl;
SetColor();
printMultiTree(root);
cout << endl;
animateTraversal(root);
SetColor(3, 0);
cout << "高度是: ";
SetColor();
cout << calculateHeight(root);
cout << endl;
SetColor(3, 0);
cout << "节点数: ";
SetColor();
cout << calculateNodeCount(root) << endl <<endl;
}
};
#endif| // 从文件中输入节点数据和位置(可随意插入任意个数节点) |
|
打开指定的文件,并逐行读取文件内容。 对于每行内容,解析节点名称和其父节点名称。 如果父节点名称为"NULL",将其作为根节点或子节点。 如果父节点名称不为"NULL",在树中查找对应的节点,然后将当前节点插入到父节点的子节点列表中。 |
| // 输出到文件 |
|
1. preOrderTraversal函数:递归地对树进行先根(前序)遍历,将遍历结果输出到给定的文件输出流中。如果当前节点为空,直接返回;否则,首先将当前节点的数据写入文件,然后对当前节点的每个子节点进行先根遍历。 2. postOrderTraversal函数:递归地对树进行后根(后序)遍历,将遍历结果输出到给定的文件输出流中。如果当前节点为空,直接返回;否则,首先对当前节点的每个子节点进行后根遍历,然后将当前节点的数据写入文件。 3. saveMultiTreeToFile函数:通过先根遍历和后根遍历将树的遍历结果写入到指定的文件中。先打开指定文件,然后在文件流上执行先根遍历和后根遍历操作,将遍历结果写入文件,最后关闭文件流。如果文件成功打开,打印成功写入信息;如果无法打开文件,打印写入失败信息。 通过这种设计,实现了将多叉树的先根遍历和后根遍历结果保存到指定文件的操作,并提供了针对文件操作的错误处理。 |
|
// 找父节点 |
|
1. 该函数接受三个参数:当前节点指针node、目标值value、node父节点指针parent,初始调用时parent设为null。 2. 首先检查当前节点是否为空,如果为空,则直接返回nullptr,表示未找到父节点。 3. 接着检查当前节点的数据是否等于目标值,如果相等,说明当前节点即为目标节点,返回其父节点指针parent。 4. 对当前节点每个子节点递归调用该函数,将当前节点设为其父节点,继续在子节点中查找目标值的父节点。 5. 如果递归查找的结果不为空,说明在子节点中找到了目标节点,则将结果直接返回。 6. 如果当前节点及其子节点中都未找到目标节点,则最终返回nullptr,表示未找到父节点。 通过这种设计,实现了对多叉树中任意节点的父节点进行查找的功能,并且处理了节点为空、节点为目标节点、以及在子节点中查找的情况。 |
|
// 找兄弟节点 |
|
这段代码用于找到多叉树中指定节点的兄弟节点,其设计思路如下: 1. 首先通过调用findParentNode函数找到指定节点的父节点。 2. 创建一个存储兄弟节点的vector<TreeNode*>容器brothers。 3. 如果父节点存在(即不为nullptr),则遍历父节点的每个子节点,将不等于目标值的子节点加入brothers容器中,即除了目标节点自身外的其他子节点。 4. 返回brothers容器,其中包含了指定节点的所有兄弟节点。 通过这种设计,实现了查找多叉树中指定节点的兄弟节点的功能,并且处理了节点无父节点的情况。 |
|
// 找孩子节点 |
|
1. 创建一个空的 vector<TreeNode*> 类型的容器 childrenList,用于存储节点的子节点。 2. 首先检查输入的节点是否为空,如果为空,则直接返回空的 childrenList,表示当前节点没有子节点。 3. 对于非空节点,遍历当前节点的 children 列表,将每个子节点加入 childrenList 容器中。 4. 返回包含当前节点所有子节点的 childrenList 容器,完成节点的子节点收集操作。 通过这种设计,实现了查找和收集多叉树中指定节点的子节点,并在节点为空时能够正确处理并返回空的子节点列表。 |
|
// 插入一个节点作为上一个节点的子节点 |
|
1. 首先检查父节点是否为空。如果父节点为空,则表示树为空,此时将新建一个值为value的节点作为根节点。 2. 如果父节点不为空,新建一个值为value的节点作为要插入的子节点。然后将该子节点加入到父节点的children容器中,即作为其子节点。 通过这种设计,实现了在多叉树中根据父节点插入新的子节点的功能。 |
|
// 根据值删除节点 // 判断是否存在这个节点(是否是可删除的) // 删除结点 |
|
1. deleteSubtree函数:用于递归删除子树。首先检查当前节点是否为空,如果为空则直接返回;然后遍历当前节点的所有子节点,对每个子节点调用自己,递归删除所有子树;最后删除当前节点。 2. deleteNodeAndSubtree函数:用于删除指定值节点及其子树。先检查根节点是否为空,若为空返回false;若根节点为目标节点,调用deleteSubtree直接删除根节点及其所有子节点并返回true;若不是目标节点,则在根节点的子节点列表中查找目标节点:若找到目标节点,删除子树并移除当前子节点;若未找到,递归调用自己在子树中继续查找。 通过这种设计,实现了在多叉树中删除目标节点及其子树的功能,并且对节点为空、节点为目标节点、以及在子节点中查找的情况都进行了正确的处理。 |
|
// 修改结点 |
|
较为简单,故未编写函数,直接体现在main函数case(3)中 1. 利用findNode函数查找并定位到对应的节点。 2. 如果查找到的节点正好是根节点,需要给出相应提示并结束修改操作。 3. 如果找不到对应的节点,也向用户给出相应提示并结束修改操作。 4. 如果找到了目标节点,再次通过输入获取用户期望的新值,并将节点的值更新为新值。 通过这样的设计,用户能够根据输入来指定要修改的节点并进行相应的值更新操作,同时也给出了对应的错误提示。 |
|
// 计算高度 |
|
1. 若当前节点为空,则返回高度0。 2. 遍历当前节点的所有子节点,对每个子节点进行递归调用calculateHeight函数,以计算每棵子树的高度。 3. 取得当前节点的所有子节点中最大的子树高度,即maxHeight。 4. 最终的子树高度为maxHeight加上当前节点自身的高度1,即maxHeight + 1。 通过这种设计,实现了对多叉树或者节点的高度进行计算,递归地考虑了每个子树的高度,最终得到整棵子树的高度。 |
|
// 计算节点数 |
|
1. 若当前节点为空,则返回节点数0。 2. 初始化计数值为1,表示当前节点本身。 3. 遍历当前节点每个子节点,对每个子节点调用calculateNodeCount函数,将返回的子树节点数量累加到计数值中。 4. 返回累加后的计数值,即为整个子树的节点数量。 通过这种设计,实现对多叉树或节点的子树节点数量进行计算,递归考虑每个子树节点数量,最终得整棵子树的节点数。 |
|
// 找到结点 |
|
1. 若当前节点为空,则返回nullptr,表示未找到目标节点。 2. 首先检查当前节点的数据是否等于目标名称,如果相等,说明当前节点即为目标节点,返回当前节点指针。 3. 对当前节点的每个子节点进行递归调用findNode函数,将子节点作为当前节点,继续在子节点中查找目标名称节点。 4. 如果在当前节点的子节点或子节点的子节点中找到了目标节点,则将找到的节点指针直接返回。 5. 若当前节点及其子节点中都未找到目标节点名称,则最终返回nullptr,表示未找到目标节点。 通过这种设计,实现在多叉树中查找指定名称的节点,并处理节点为空、节点为目标节点、以及在子节点中查找的情况。 |
|
// 找到指定结点在第几层 |
|
1. 若根节点为空,则返回-1,表示树为空,无法找到层级。 2. 创建一个队列nodesQueue,用于进行层序遍历并记录节点的层级。 queue<pair<TreeNode*, int>> nodesQueue; 3. 将根节点和其层级1作为pair加入到队列中。 nodesQueue.push(make_pair(root, 1)); 4. 在队列不为空的情况下,循环执行以下步骤: TreeNode* current = nodesQueue.front().first; - 取出队列中的第一个节点和该节点的层级。 int level = nodesQueue.front().second; - 检查当前节点的数据是否等于目标值,如果相等,则表示找到了目标节点,直接返回其所在的层级。 - 遍历当前节点的每个子节点,将子节点以及其对应的层级加入到队列中,层级加1。 5. 若遍历完整棵树后都未找到目标节点,最终返回-1,表示未找到节点所在的层级。 通过这种设计,实现了在多叉树中查找指定节点所在的层级,并且使用层序遍历的方式逐层搜索目标节点,根据结果返回节点所在的层级。 |
|
// 移动结点 |
|
1. 首先,根据目标值和目标位置值分别获取它们在树中的层级,如果其中有一个值不存在,或者目标值在目标位置之下,即目标值的层级小于目标位置的层级,则无法进行移动,直接返回false。 2. 接着,查找目标值和目标位置值的父节点,如果找不到他们,则无法进行移动,直接返回false。 3. 在目标值的父节点中查找目标值在其子节点中的位置,然后将其移除。 4. 最后,将目标值移动到目标位置的子节点中,并返回true,表示移动操作成功;如果未执行成功的话,返回false。 通过这种设计,实现了在多叉树中移动节点到另一个位置并替换节点的功能,并对错误情况进行了相应的处理。 |
|
//先根、后根遍历 |
|
1. 先根遍历函数 preOrderTraversal: - 若当前节点为空,则直接返回。。 - 遍历当前节点的每个子节点,对每个子节点进行递归调用preOrderTraversal,处理每个子节点。 2. 后根遍历函数 postOrderTraversal: - 若当前节点为空,则直接返回。 - 对当前节点的每个子节点进行递归调用postOrderTraversal,处理每个子节点。 |
|
//层序遍历 |
|
1. 首先检查根节点是否为空,如果为空则直接返回。 2. 创建一个队列 nodesQueue,并将根节点加入队列。 3. 在队列不为空的情况下,循环执行以下步骤: - 取出队列中的第一个节点 current。 - 以打印节点数据。 - 将当前节点的每个子节点加入队列中,以便后续继续遍历子节点。 |
|
// 树形输出 |
|
1. 首先检查当前节点是否为空。如果为空则直接返回,不进行任何打印操作。 2. 如果当前节点不为空,首先根据节点是不是最后一个子节点,打印对应的前缀,用以展示树的分支结构。 3. 根据节点的数据是否为特定值,设置节点的打印颜色,以突出显示特定节点。 4. 对当前节点的每个子节点进行递归调用 printMultiTree 函数,打印子节点的数据和对应的分支结构。 通过这种设计和递归调用,实现了对整个多叉树结构清晰打印,并能够通过特定颜色和分支结构直观展示树的层次结构。 |
| // 动画演示输出顺序 |
|
1. printaniMultiTree函数: - 与前面所描述的树形输出函数类似,但增加了一个参数cur,用以表示当前处理的节点。 - 在输出时,如果当前节点是目标节点cur,则使用特定颜色输出,以突出显示该节点。 2. preOrderprint函数: 对树进行先根遍历,并在每个节点遍历完毕后输出遍历结果,并调用printaniMultiTree函数展示树的结构,并通过延时操作(Sleep)和清屏操作(system("cls"))产生动画效果。 3. postOrderprint函数: 对树进行后根遍历,并在每个节点遍历完毕后输出遍历结果,并调用printaniMultiTree函数展示树的结构,并通过延时操作(Sleep)和清屏操作(system("cls"))产生动画效果。 4. levelOrderprint函数: 对树进行层序遍历,并在每个节点遍历完毕后输出遍历结果,并调用printaniMultiTree函数展示树的结构,并通过延时操作(Sleep)和清屏操作(system("cls"))产生动画效果。 通过这种设计,实现了对树的各种遍历操作,并以动画形式展示了遍历顺序和树的结构,增加了程序的可视化效果。 |
源程序代码 main.cpp
int main()
{
MultiTree tree; tree.createTreeFromFile("input.txt");
SetColor(3, 0); cout << "第一次打开从input.txt中读取数据" << endl;
tree.coutmodel(); SetColor(0, 15);
cout << "1:删除某个节点 2:增加一个节点 3:修改节点内容 4:移动某个节点 5:查询某个节点 6:动画展示遍历 7:退出并保存至文件";
SetColor(); cout << endl;
while (1) {
int swi = 0; bool flag = 0; cin >> swi;
switch (swi){
case(1):{
SetColor(0, 15); cout << "谁被逐出家门了:"; SetColor(); cout << endl;
string edit; cin >> edit;
if (edit == tree.root->data){
SetColor(11, 0); cout << "无法删除该根结点"; SetColor(); cout << endl; break;}
bool flag1 = (tree.deleteNodeAndSubtree(tree.root, edit));
if (flag1 == 0){
SetColor(11, 0); cout << "该人不在其中"; SetColor(); cout << endl; break; }
tree.coutmodel(); break;}
case(2):{
int choose = 0; SetColor(0, 15);
cout << "1:找到了先人(在树中根据孩子节点插入父亲节点) 2:找到了后代(在树中根据父亲节点插入孩子节点)"; SetColor(); cout << endl; cin >> choose;
if (choose == 1){
SetColor(0, 15); cout << "谁找到了先人"; SetColor(); cout << endl;
string add; cin >> add;
TreeNode* parent = tree.findParentNode(tree.root, add);
TreeNode* cur = tree.findNode(tree.root, add);
if (cur == tree.root){
SetColor(11, 0); cout << "无法修改该根结点" << endl; SetColor(); break;}
if (parent == nullptr){
SetColor(11, 0); cout << "该人不在其中" << endl; SetColor(); break;}
if (parent != nullptr){
SetColor(0, 15); cout << "他的祖先叫?"; SetColor(); cout << endl;
string teacher; cin >> teacher;
TreeNode* child = tree.findNode(tree.root, add);
TreeNode *teacherptr = tree.findNode(tree.root, teacher);
if(teacherptr!=nullptr && child != nullptr){teacherptr->addChild(child);}
if (teacherptr==nullptr && child != nullptr){
for (auto grandchild : parent->children){
if (grandchild->data == add){
tree.insertChild(parent, teacher);
TreeNode* tmp = tree.findNode(tree.root, teacher);
tmp->addChild(child);}}}
parent->children.erase(remove(parent->children.begin(), parent->children.end(), child), parent->children.end()); }}
if (choose == 2){
SetColor(0, 15); cout << "谁找到了后代"; SetColor(); cout << endl;
string add; cin >> add;
TreeNode* parent = tree.findNode(tree.root, add);
if (parent == nullptr){
SetColor(11, 0); cout << "该人不在其中" << endl; SetColor(); break;}
SetColor(0, 15); cout << "他的孩子叫?"; SetColor(); cout << endl;
string student; cin >> student;
TreeNode* past = tree.findNode(tree.root, student);
TreeNode* pastpar = tree.findParentNode(tree.root, student);
if (tree.findNode(past, parent->data)){
SetColor(11, 0); cout << "这违反常理" << endl; SetColor(); break; }
if(past == nullptr){ tree.insertChild(parent, student);}
if(past != nullptr){ parent->addChild(past);
pastpar->children.erase(remove(pastpar->children.begin(), pastpar->children.end(), past), pastpar->children.end());}}
tree.coutmodel(); break;}
case(3):{
SetColor(0, 15); cout << "想要修改哪个节点的值"; SetColor(); cout << endl;
string findstr; cin >> findstr;
TreeNode* find = tree.findNode(tree.root, findstr);
if (find == tree.root){
SetColor(11, 0); cout << "无法修改该根结点" << endl; SetColor(); break;}
if (find == nullptr) {
SetColor(11, 0); cout << "该人不在其中" << endl; SetColor(); break;}
SetColor(0, 15); cout << "想要修改为?"; SetColor(); cout << endl;
string setstr; cin >> setstr;
find->data = setstr; tree.coutmodel(); break;}
case(4):{
SetColor(0, 15); cout << "想要移动哪个节点"; SetColor(); cout << endl;
string move; cin >> move;
TreeNode* moveptr = tree.findNode(tree.root, move);
if (moveptr == tree.root){
SetColor(11, 0); cout << "无法修改该根结点" << endl; SetColor(); break;}
if (moveptr == nullptr){
SetColor(11, 0); cout << "该人不在其中" << endl; SetColor(); break; }
SetColor(0, 15); cout << "移动至哪个节点的位置"; SetColor(); cout << endl;
string end; cin >> end;
TreeNode* endptr = tree.findNode(tree.root, end);
if (endptr == nullptr){
SetColor(11, 0); cout << "该人不在其中" << endl; SetColor(); break;}
TreeNode* parent = tree.findParentNode(tree.root, end);
TreeNode* child = tree.findNode(tree.root, end);
if ((tree.moveAndReplaceNode(tree.root, move, end)) == 1){
parent->children.erase(remove(parent->children.begin(), parent->children.end(), child), parent->children.end());
if (tree.findNodeLevel(tree.root, move) >= tree.findNodeLevel(tree.root, end)){tree.coutmodel();}}
if (tree.findNodeLevel(tree.root, move) < tree.findNodeLevel(tree.root, end)){
SetColor(11, 0); cout << "无法向后移动 "; SetColor(); cout << endl;} break;}
case(5):{
SetColor(0, 15); cout << "想要查找哪个节点"; SetColor(); cout << endl;
string value; cin >> value;
TreeNode* find = tree.findNode(tree.root, value);
int level = tree.findNodeLevel(tree.root, value);
if (find == nullptr) {
SetColor(11, 0); cout << "该人不在其中"; SetColor(); cout << endl;}
else { cout << "在第"; SetColor(11, 0); cout << level; SetColor(); cout << "层";
if (level == 1) {
SetColor(11, 0); cout << ",已经是root了"; SetColor(); cout << endl;}
if (level != 1) {
cout << ",他的先人为"; SetColor(11, 0);
cout << tree.findParentNode(tree.root, value)->data;
SetColor(); cout << ",他的兄弟为"; SetColor(11, 0);
vector<TreeNode*> brotherList;
brotherList = tree.findBrotherNodes(tree.root, value);
if (brotherList.size() != 0) {
for (int i = 0; i < (int)brotherList.size(); i++) {
cout << brotherList[i]->data << " ";}}
if ((int)brotherList.size() == 0) { cout << "空";}
SetColor(); cout << ",他的孩子为"; SetColor(11, 0);
vector<TreeNode*> childrenList;
childrenList = tree.findChildrenNodes(find);
if (childrenList.size() != 0) {
for (int i = 0; i < (int)childrenList.size(); i++){
cout << childrenList[i]->data << " ";}}
if ((int)childrenList.size() == 0) { cout << "空";}
SetColor(); cout << endl;}} break;}
case(6):{
int c; SetColor(0, 15); cout << "先根:1 后跟:2 层序:3"; SetColor();
cout << endl; cin >> c;
if (c == 1){ tree.preOrderprint(tree.root); tree.coutmodel();}
if (c == 2){ tree.postOrderprint(tree.root); tree.coutmodel(); }
if (c == 3){ tree.levelOrderprint(tree.root); tree.coutmodel();}
if (c != 1 && c != 2 && c != 3){
SetColor(0, 4); cout << "输入有误"; SetColor(); cout << endl;} break;}
case(7):{ flag = 1; break;}
default:{ SetColor(0, 4); cout << "输入有误"; SetColor(); cout << endl; }}
if (flag == 1){ break;}
SetColor(0, 15);
cout << "1:删除某个节点 2:增加一个节点 3:修改节点内容 4:移动某个节点 5:查询某个节点 6:动画展示遍历 7:退出并保存至文件";
SetColor(); cout << endl;}
tree.saveMultiTreeToFile(tree.root, "output.txt");
}
实验结果
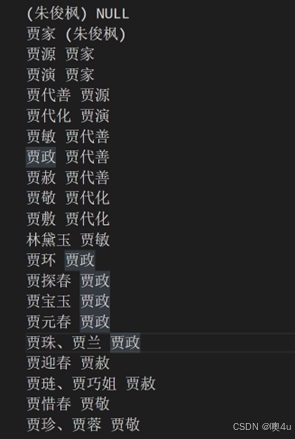
| 测试用例(input.txt) |
|
|
| 运行结果截图 |
|
功能1:树形显示,菜单,计算并显示其高度、结点数及三种遍历顺序,从文件中读取数据 |
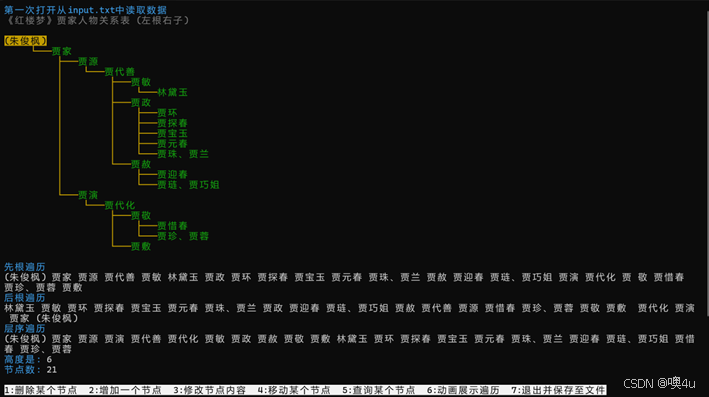 |
|
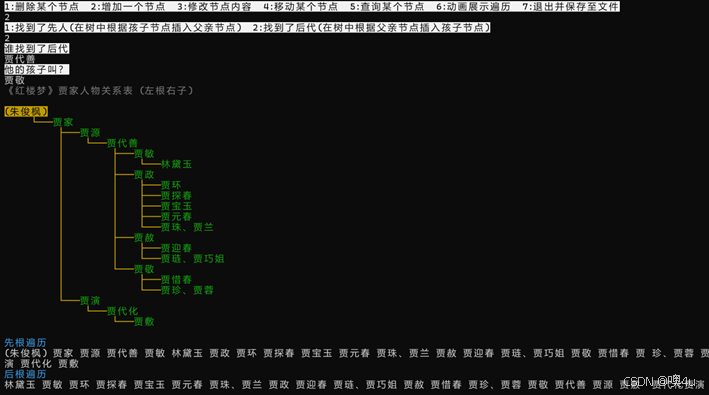
功能2:删除和分别在前、后新增结点,修改后立即显示二叉树 |
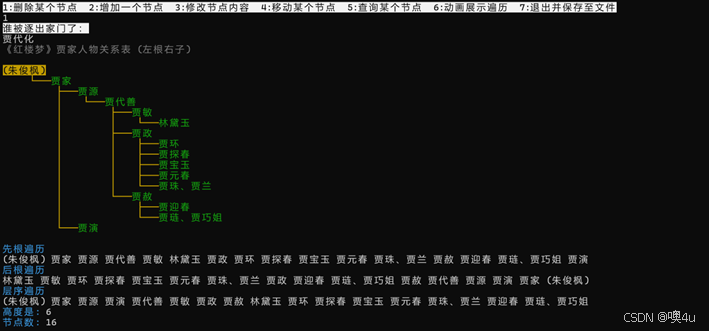 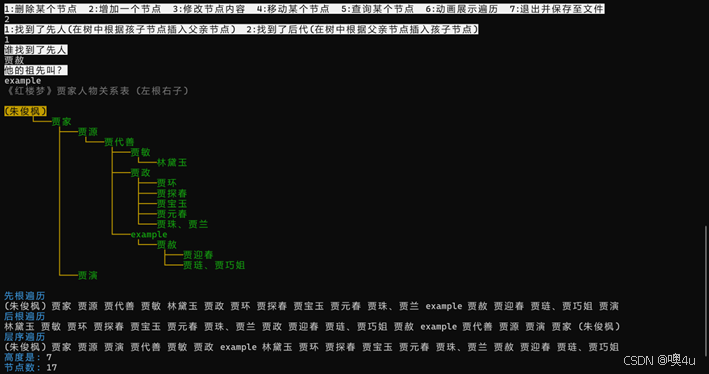 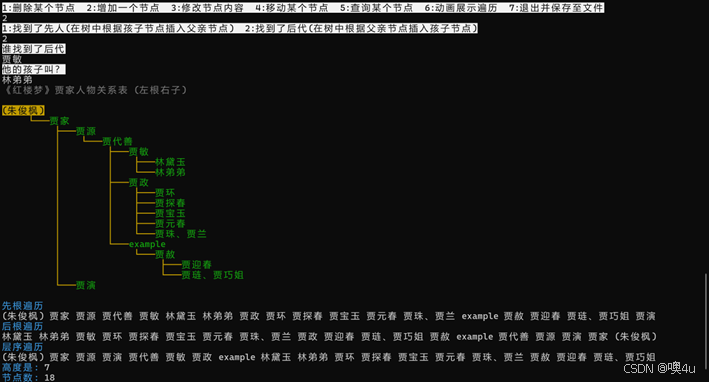  |
|
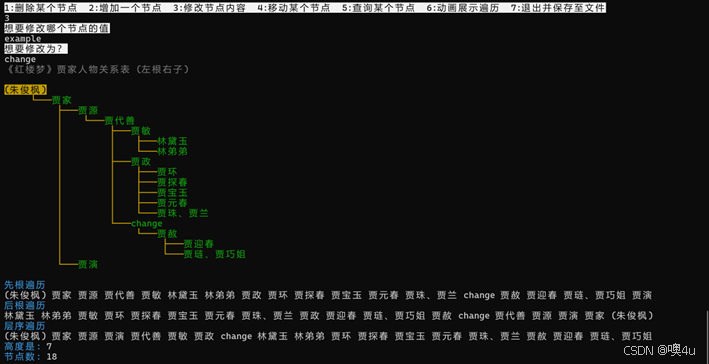
功能3:修改节点内容,修改后立即显示二叉树 |
 |
|
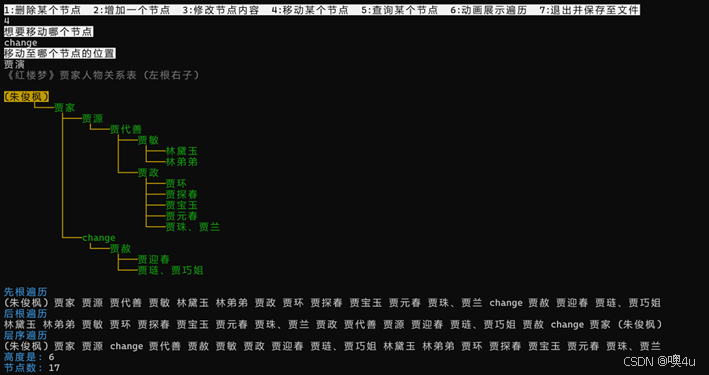
功能4:移动结点,修改后立即显示二叉树 |
 |
|
功能5:查询节点信息 |
 |
|
功能6:动画展示遍历 |
      |
|
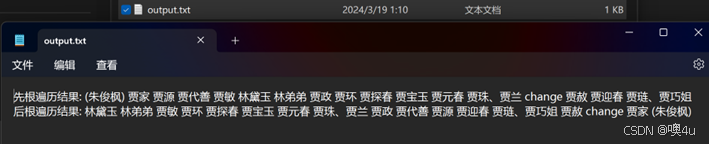
功能7:退出并保存至output.txt文件中 |
  |
|
功能8:异常输入检查 |
   |
算法分析
- createTreeFromFile:遍历文件内容并根据节点信息构建多叉树,时间复杂度为O(n),其中n是节点的个数。
- preOrderTraversal和postOrderTraversal:递归地遍历树的所有节点,时间复杂度为O(n),其中n是节点的个数。
- saveMultiTreeToFile:内部包含先根遍历和后根遍历,因此时间复杂度也为O(n),其中n是节点的个数。
- findParentNode和findNode:在多叉树中查找父节点和指定节点,最坏情况下的时间复杂度为O(n),其中n是节点的个数。
- findBrotherNodes和findChildrenNodes:查找兄弟节点和子节点,时间复杂度为O(k),其中k是节点的子节点个数。
- insertChild和moveAndReplaceNode:在树中插入和移动节点,时间复杂度取决于查找父节点的时间复杂度,最坏情况下为O(n),其中n是节点的个数。
- deleteSubtree和deleteNodeAndSubtree:删除节点及其子树的操作,时间复杂度也为O(n),其中n是节点的个数。
- calculateHeight和calculateNodeCount:计算树的高度和节点数,递归遍历每个节点,时间复杂度为O(n),其中n是节点的个数。
- findNodeLevel:在树中查找节点所在的层级,最坏情况下的时间复杂度为O(n),其中n是节点的个数。
- printaniMultiTree、preOrderprint、postOrderprint和levelOrderprint:这些函数会递归遍历节点并输出,所以时间复杂度与树的节点数成正比,最差情况下为O(n),其中n是节点的个数。
- animatedPreOrderTraversal、 animatedPostOrderTraversal、 animatedLevelOrderTraversal:这些函数在树上进行遍历并输出,时间复杂度与树的节点数成正比,最差情况下为O(n),其中n是节点的个数。
综上所述,大多数操作的时间复杂度都与树的节点数量成正比,主要受树的结构和深度影哨。因此,在最坏情况下,这些操作的时间复杂度为O(n),其中n是节点的个数。
在解决“以动画形式输出遍历过程”这一问题时,我原本想法是对于先根和后根遍历的情况,自上而下或自下而上输出即可,但在层序遍历时这一算法行不通了,于是便想到使用一个指针current来表示当前遍历到的结点,在print函数中加上if(root==current)的判断条件来突出显示,并通过延时再清屏以完成动画的效果。本来还想创建多线程使文字和树形同时输出,但难以实现。

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容







所有评论(0)