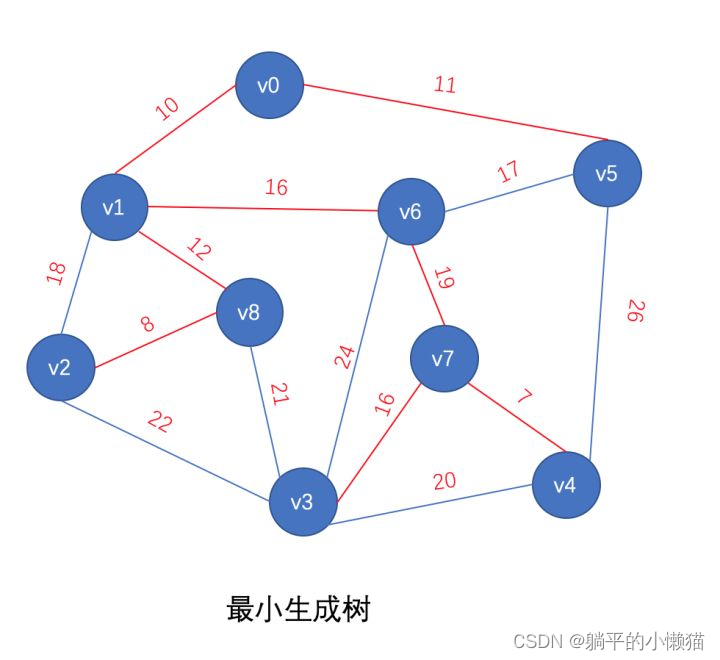
最小生成树是指在一个加权无向连通图中，生成一棵边权值最小的生成树。生成树是一个无向树，它包含了原图中的所有顶点，并且一定是一棵树（没有环）。最小生成树算法的输出结果是一颗包含所有顶点的生成树，且该生成树的边权之和最小。

最小生成树算法包括Prim算法和Kruskal算法。

Prim算法：从任意一点出发，将该点加入生成树中，然后不断选择与当前生成树相连元素中权值最小的边加入生成树。

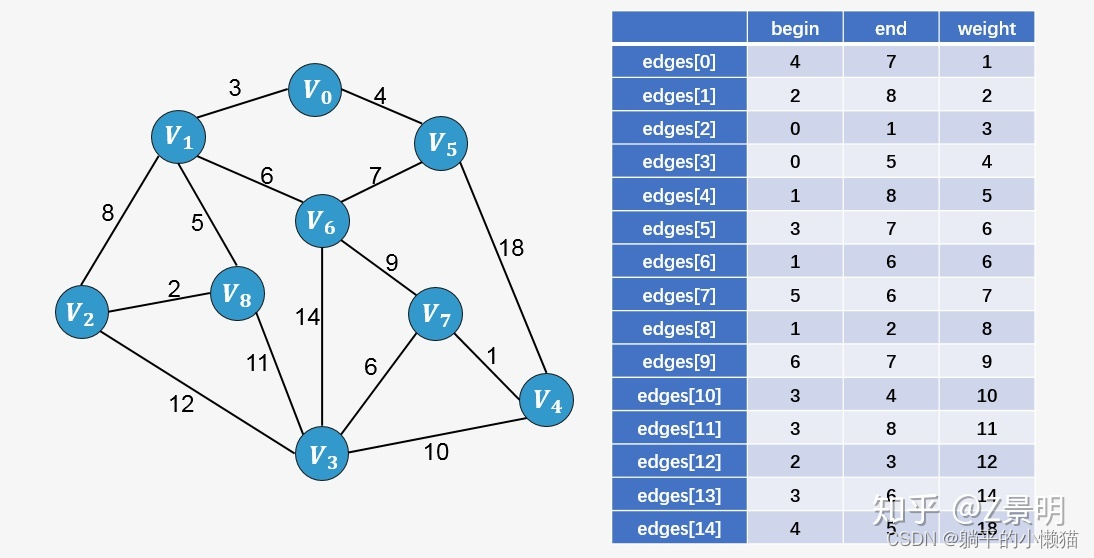
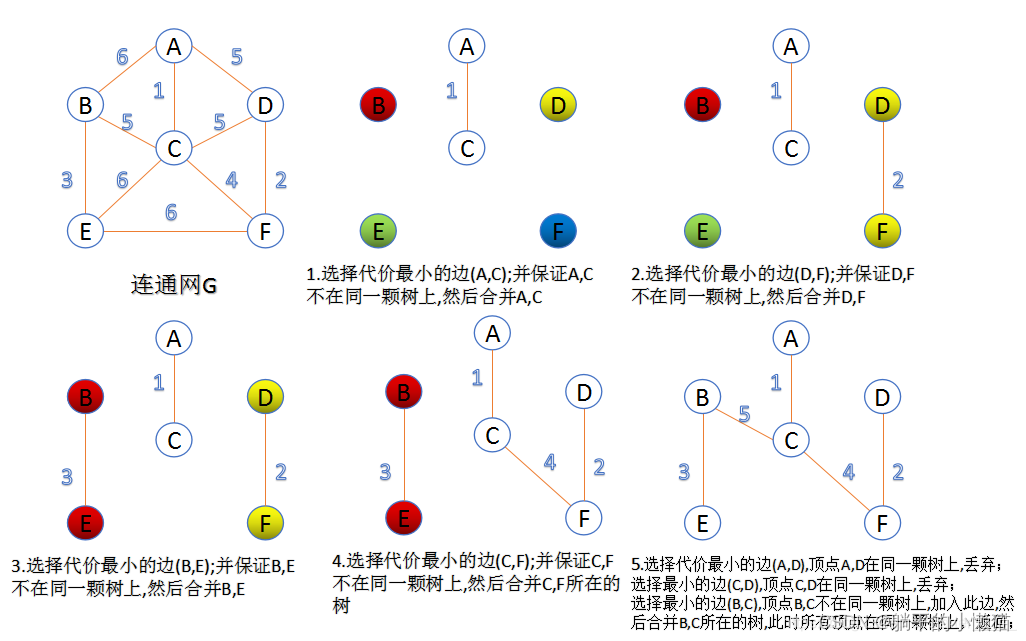
Kruskal算法：将所有边按权重从小到大排序，依次把边加入生成树中，保证不会形成环，直到加入n-1条边为止，其中n为图的总节点数。

一、C 实现数据结构之最小生成树源码及详解

以下是 C 语言实现最小生成树 Prim 算法的源码及详解：

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define MAX 1000    // 最大顶点数

int graph[MAX][MAX];    // 图
int v[MAX];             // 标记顶点是否已经在生成树中
int dis[MAX];           // 记录生成树到每个顶点的距离
int pre[MAX];           // 记录生成树中每个顶点的前一个顶点

void prim(int n, int start)
{
    int i, j, k, min;

    // 初始化
    for (i = 0; i < n; i++) {
        dis[i] = graph[start][i];
        v[i] = 0;
        pre[i] = start;
    }
    v[start] = 1;
    pre[start] = -1;

    // 依次寻找 n-1 个顶点加入生成树
    for (i = 1; i < n; i++) {
        // 找到距离生成树最近的顶点
        min = MAX;
        k = -1;
        for (j = 0; j < n; j++) {
            if (!v[j] && dis[j] < min) {
                min = dis[j];
                k = j;
            }
        }

        // 将该顶点加入生成树
        v[k] = 1;

        // 更新与该顶点相邻的顶点到生成树的距离
        for (j = 0; j < n; j++) {
            if (!v[j] && graph[k][j] < dis[j]) {
                dis[j] = graph[k][j];
                pre[j] = k;
            }
        }
    }
}

void print_mst(int n)
{
    int i;
    printf("最小生成树：\n");
    for (i = 0; i < n; i++) {
        if (pre[i] != -1) {
            printf("(%d, %d) ", pre[i]+1, i+1);
        }
    }
    printf("\n");
}

int main()
{
    int n, m, start;
    int i, j, weight, u, v;

    scanf("%d%d%d", &n, &m, &start);

    // 初始化图
    for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) {
            graph[i][j] = MAX;
        }
    }

    // 读入边
    for (i = 0; i < m; i++) {
        scanf("%d%d%d", &u, &v, &weight);
        graph[u-1][v-1] = weight;
        graph[v-1][u-1] = weight;
    }

    prim(n, start-1);
    print_mst(n);

    return 0;
}

算法说明：

• 核心思路：从一个顶点开始，依次将距离生成树最近的顶点加入生成树中，直到所有的顶点都被加入到生成树中。
• 数据结构：使用邻接矩阵来表示图，数组 dis 记录生成树到每个顶点的距离，数组 pre 记录生成树中每个顶点的前一个顶点，数组 v 标记顶点是否已经在生成树中。
• 算法步骤：
  1. 初始化：将起始点加入生成树中，用 dis 数组记录起始点到每个顶点的距离，将所有顶点标记为未加入生成树。
  2. 依次寻找 n-1 个顶点加入生成树：
     • 找到距离生成树最近的顶点：遍历所有未加入生成树的顶点，选取距离生成树最近的顶点。
     • 将该顶点加入生成树：将该顶点标记为已加入生成树。
     • 更新与该顶点相邻的顶点到生成树的距离：遍历所有未加入生成树的顶点，若与该顶点相邻，则更新该顶点到生成树的距离和该顶点的前一个顶点。
  3. 输出最小生成树：遍历 pre 数组，输出每个顶点和其前一个顶点。

算法复杂度：

• 时间复杂度：O(n^2)，主要时间消耗在寻找距离生成树最近的顶点上，需要遍历所有未加入生成树的顶点。
• 空间复杂度：O(n^2)，需要使用邻接矩阵来存储图。

二、C++ 实现数据结构之最小生成树源码及详解

以下是一个 C++ 实现的最小生成树算法的示例代码及详解：

#include <bits/stdc++.h>  // 引入万能头文件
using namespace std;

const int MAXN = 1005;  // 最大节点数
const int INF = 0x3f3f3f3f;  // 防止溢出，定义一个无穷大常量

int edge[MAXN][MAXN];  // 存储边的连接情况和权值
int lowcost[MAXN];  // 存储每个节点到集合的最小权值
bool vis[MAXN];  // 标记每个节点是否已在集合中

int prim(int n) {
    memset(vis, false, sizeof(vis));  // 初始化所有节点都未被加入集合
    int ans = 0;  // 最小生成树的权值
    vis[1] = true;  // 从节点1开始，将1加入集合
    for (int i = 2; i <= n; i++) {
        lowcost[i] = edge[1][i];  // 更新集合外节点到集合的最小权值
    }
    for (int i = 1; i < n; i++) {  // 一共需要 n-1 条边
        int mincost = INF, k = 0;
        for (int j = 2; j <= n; j++) {  // 遍历所有集合外节点，找到权值最小的节点
            if (!vis[j] && lowcost[j] < mincost) {
                mincost = lowcost[j];
                k = j;
            }
        }
        vis[k] = true;  // 将权值最小的节点加入集合
        ans += mincost;  // 将新加入的边的权值累加到最小生成树的权值中
        for (int j = 2; j <= n; j++) {  // 更新集合外节点到集合的最小权值
            if (!vis[j] && lowcost[j] > edge[k][j]) {
                lowcost[j] = edge[k][j];
            }
        }
    }
    return ans;
}

int main() {
    int n, m;
    cin >> n >> m;  // 输入节点数和边数
    memset(edge, 0x3f, sizeof(edge));  // 将所有边的权值初始化为无穷大
    for (int i = 1; i <= m; i++) {
        int u, v, w;
        cin >> u >> v >> w;  // 输入一条边的两个端点和权值
        edge[u][v] = edge[v][u] = w;  // 添加一条无向边
    }
    cout << prim(n) << endl;  // 输出最小生成树的权值
    return 0;
}

该实现采用了 Prim 算法，主要思路如下：

1. 初始化所有节点都未加入集合。
2. 从节点1开始，将1加入集合，将集合外节点到集合的最小权值更新为对应的边权。
3. 找到权值最小的集合外节点k，将它加入集合，将新加入的边的权值累加到最小生成树的权值中，并更新所有集合外节点到集合的最小权值。
4. 重复步骤3，直到集合中所有节点都被加入为止。

时间复杂度为 $O(n^2)$，其中 $n$ 为节点数。在实际应用中，可以使用堆优化的 Prim 算法将时间复杂度优化至 $O(m\log n)$，其中 $m$ 为边数，但实现较为复杂。