已知由n（n≥2）个正整数构成的集合A={ |0≤ k＜n}，将其划分为两个不相交的子集和，元素个数分别是和，和中元素之和分别为和。设计一个尽可能高效的划分算法，满足最小且最大。要求：

（1）给出算法的基本设计思想。

（2）根据设计思想，采用C或C++语言描述算法，关键之处给出注释。

（3）说明你所设计算法的平均时间复杂度和空间复杂度。

注意：设计一个尽可能高效的划分算法，即设计时间复杂度和空间复杂度较好的算法为优先。

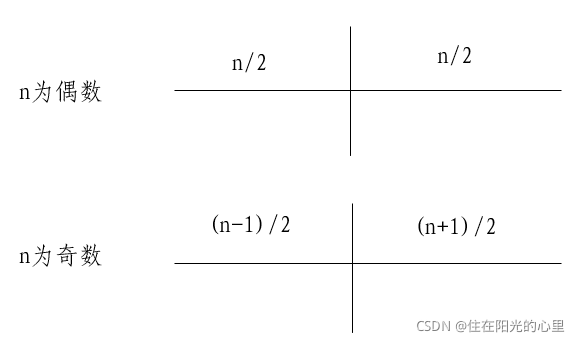
按如下划分，可满足最小且最大

// 测试代码
/*
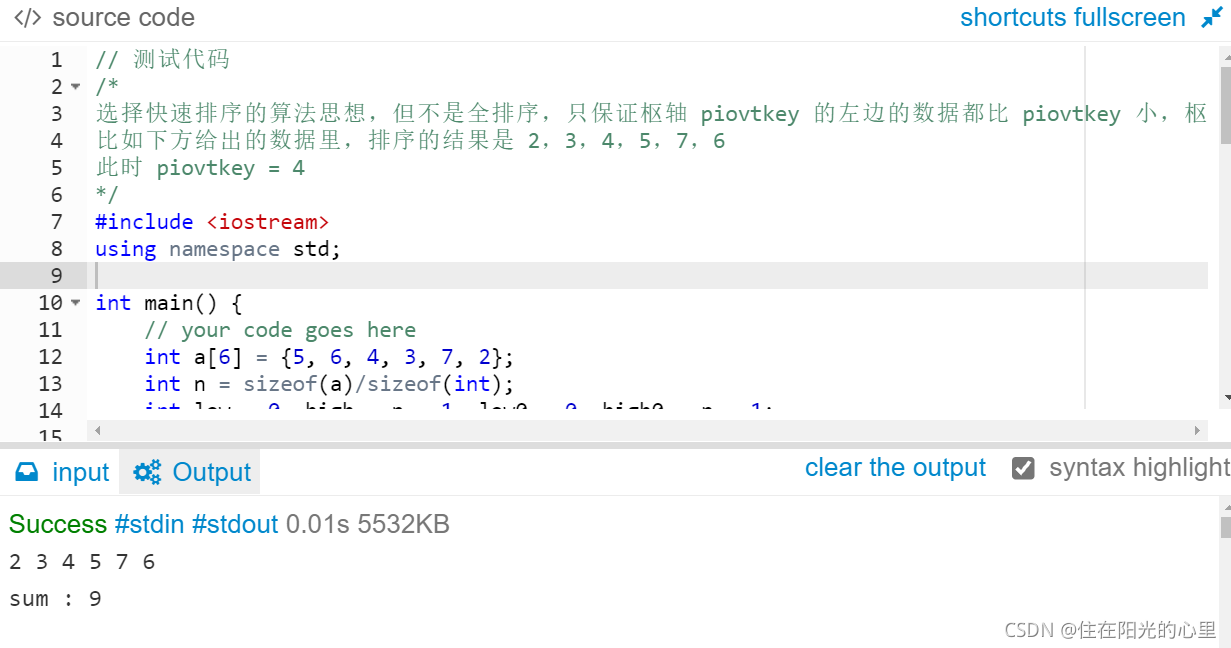
选择快速排序的算法思想，但不是全排序，只保证枢轴 piovtkey 的左边的数据都比 piovtkey 小，枢轴 piovtkey 的右边的数据都比 piovtkey 大。
比如下方给出的数据里，排序的结果是 2，3，4，5，7，6
此时 piovtkey = 4
*/
#include <iostream>
using namespace std;

int main() {
	// your code goes here
	int a[6] = {5, 6, 4, 3, 7, 2};
	int n = sizeof(a)/sizeof(int);
	int low = 0, high = n - 1, low0 = 0, high0 = n - 1;
	int flag = 1, k = n/2;
	int s1 = 0, s2 = 0;
	int piovtkey;
	while(flag){
		piovtkey = a[low];  // 选择枢轴
		while(low < high){      // 基于枢轴对数据进行划分
			while(low < high && a[high] >= piovtkey){
				--high;
			}
			if(low != high){
				a[low] = a[high];
			}
			while(low < high && a[low] <= piovtkey){
				++low;
			}
			if(low != high){
				a[high] = a[low];
			}
		}
		a[low] = piovtkey;
		if(low == k - 1){   // 若枢轴是第 n/2 个元素，划分成功
			flag = 0;
		}
		else{
			if(low < k - 1){
				low0 = ++low;
				high = high0;
			}
			else{
				high0 = --high;
				low = low0;
			}
		}
	}
	for(int i = 0; i < 6; i++){
		cout<< a[i] << " ";
	}
	cout<<endl;
	for(int j = 0; j < k; j++) s1 += a[j];
	for(int q = k; q < n; q++) s2 += a[q];
	cout<< "sum : "<< s2 - s1 <<endl;;
}

标准答案如下：

https://www.nowcoder.com/questionTerminal/c9950515d3e14b0e998a6b449ecbfeeb?mutiTagIds=597&page=1&onlyReference=false