01.认识复杂度和简单排序算法

位运算

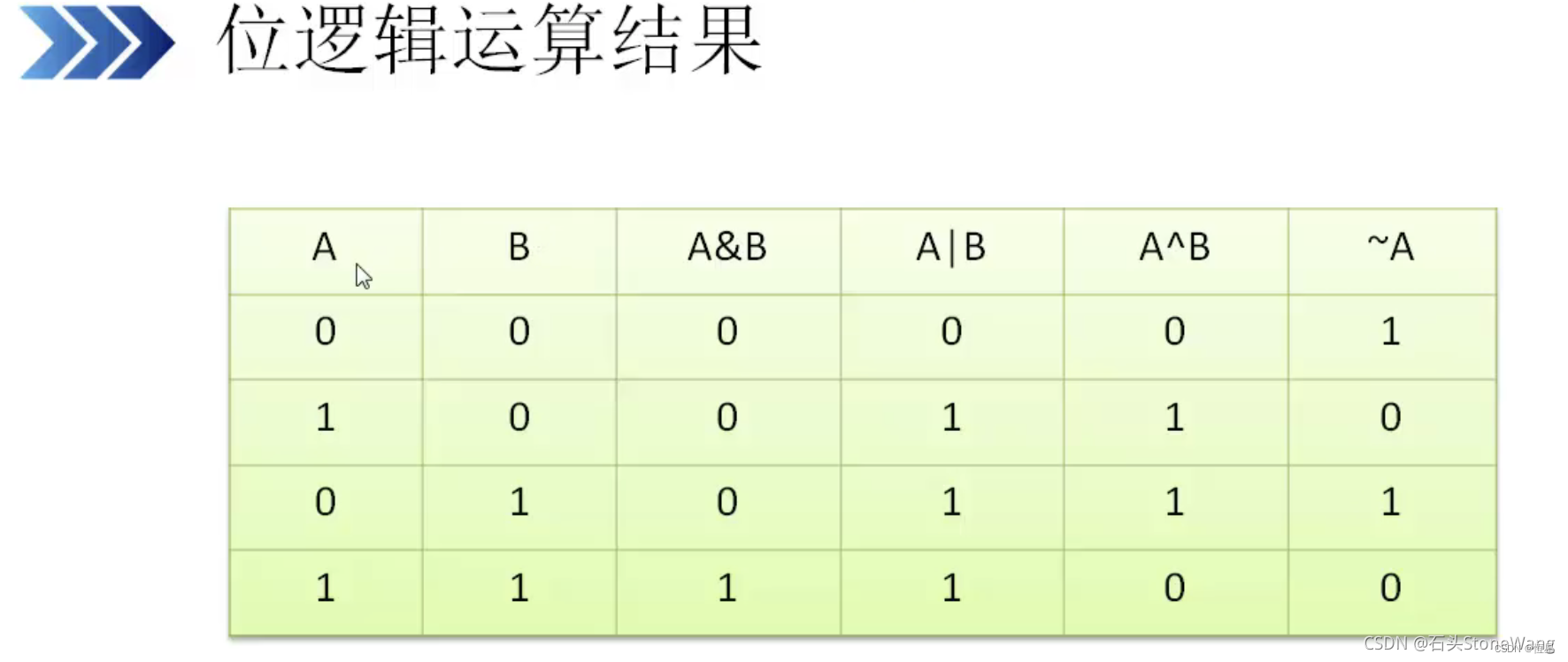
与：两个是1才是1
或：只要有一个是1就是1
异或：只有11跟或不同，其他一样。（更好的记忆方式：相同是0）
取反：0变1，1变0

异或运算（属于位逻辑运算）

• 异或运算就是无进位加法
  

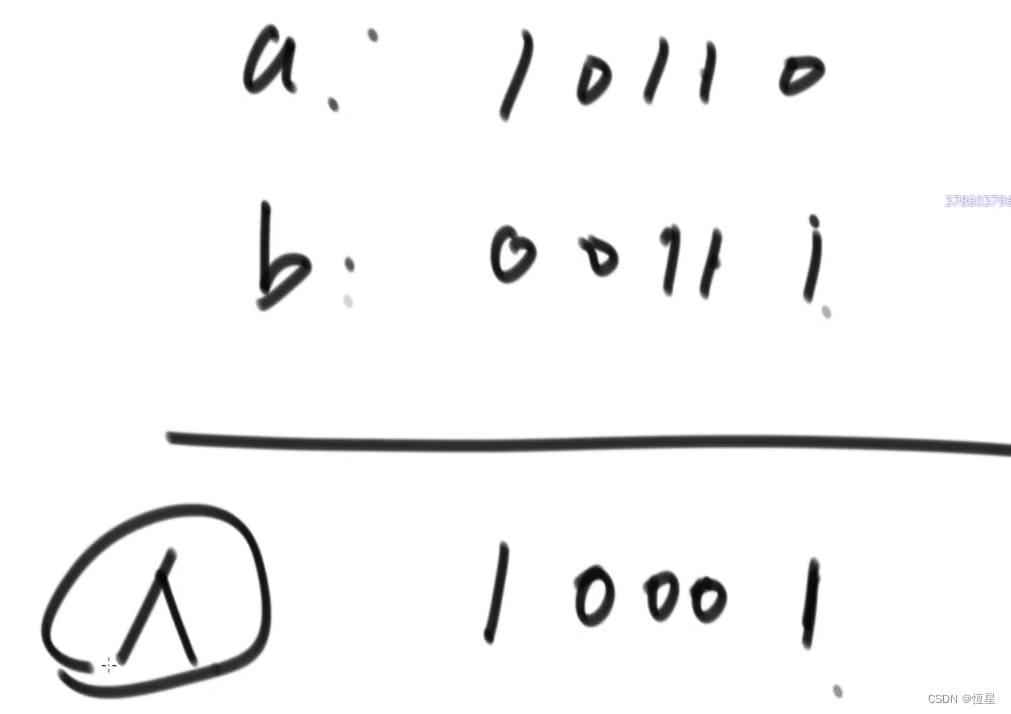
• 异或性质

1. 满足交换，结合
2. 0 ^ N=N, N ^ N=0

• 实例

1. 三行代码实现数据交换
   

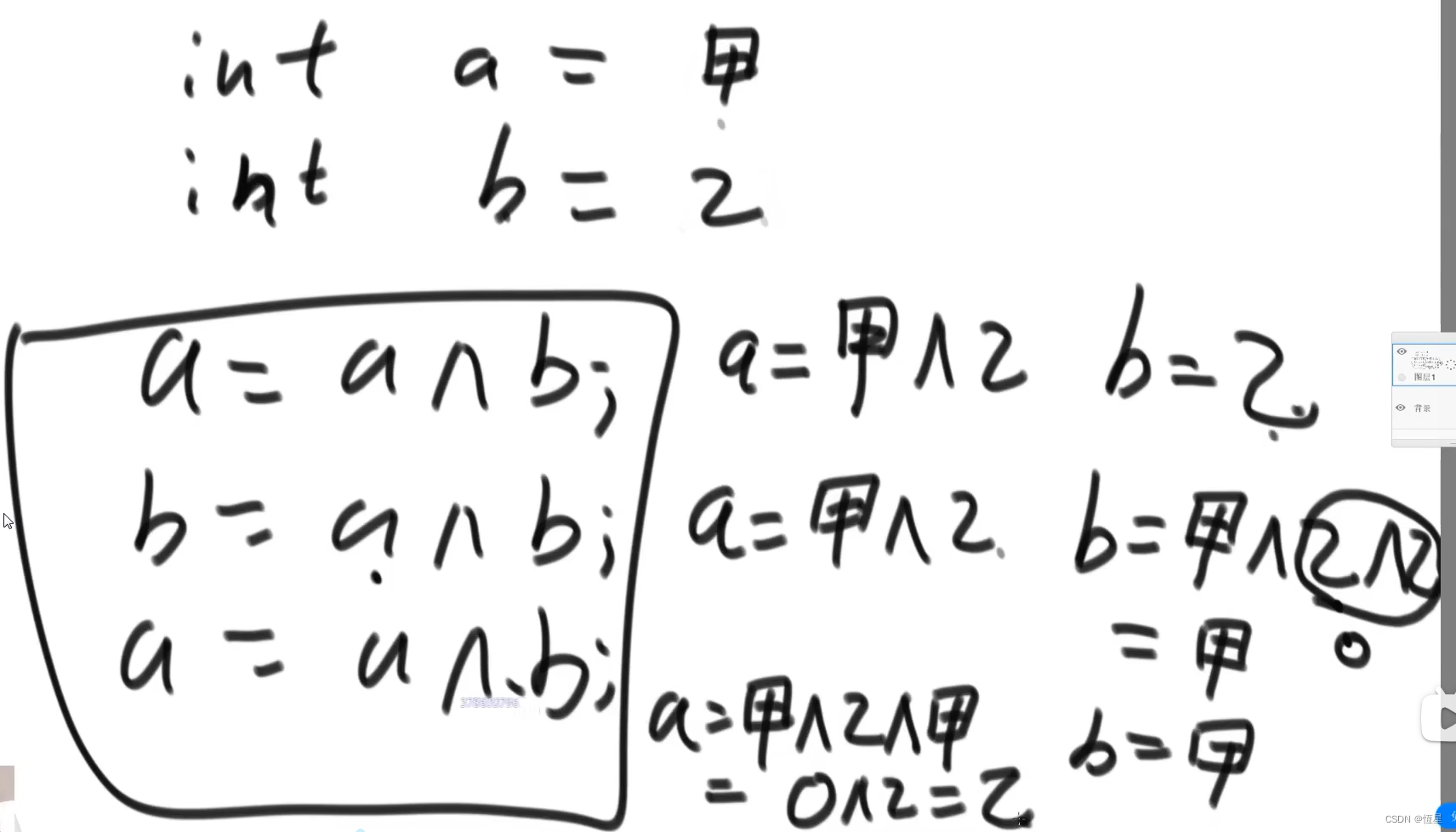
2. （1）一个数组 int arr[]，一种数出现奇数次，其余数全部出现偶数次，求奇数次的数。时间复杂度为O(n)，空间复杂度为O(1)。

   （2）一个数组 int arr[]，两种数出现奇数次，其余数全部出现偶数次，求奇数次的数。时间复杂度为O(n)，空间复杂度为O(1)。

解答：（1）创建变量eor=0，与数组的每个数进行异或运算。由于满足交换律，可让偶数次的数先异或，得0，奇数次的数异或后得本 身，0与任何数异或得这个数。则eor为奇数次的数。

（2）

创建变量eor=0，与数组的每个数进行异或运算。由于满足交换律，可让偶数次的数先异或，得0，奇数次的数异或后得本身，0与任何数异或得这个数。则eor为a ^ b。由于a!=b，则eor!=0。那么a和b肯定至少有一位上不一样，即eor肯定至少有一位是1。假设eor第八位是1，不妨设a的第八位为1，则b的第八位为0，偶数次的others里也有第八位为0或1的，分别划入指定位置。创建变量eor’=0，然后让eor’与第八位是1的所有数异或，偶数次异或为0，则eor’=a。再让eor ^ eor’（a ^ b ^ a），得b。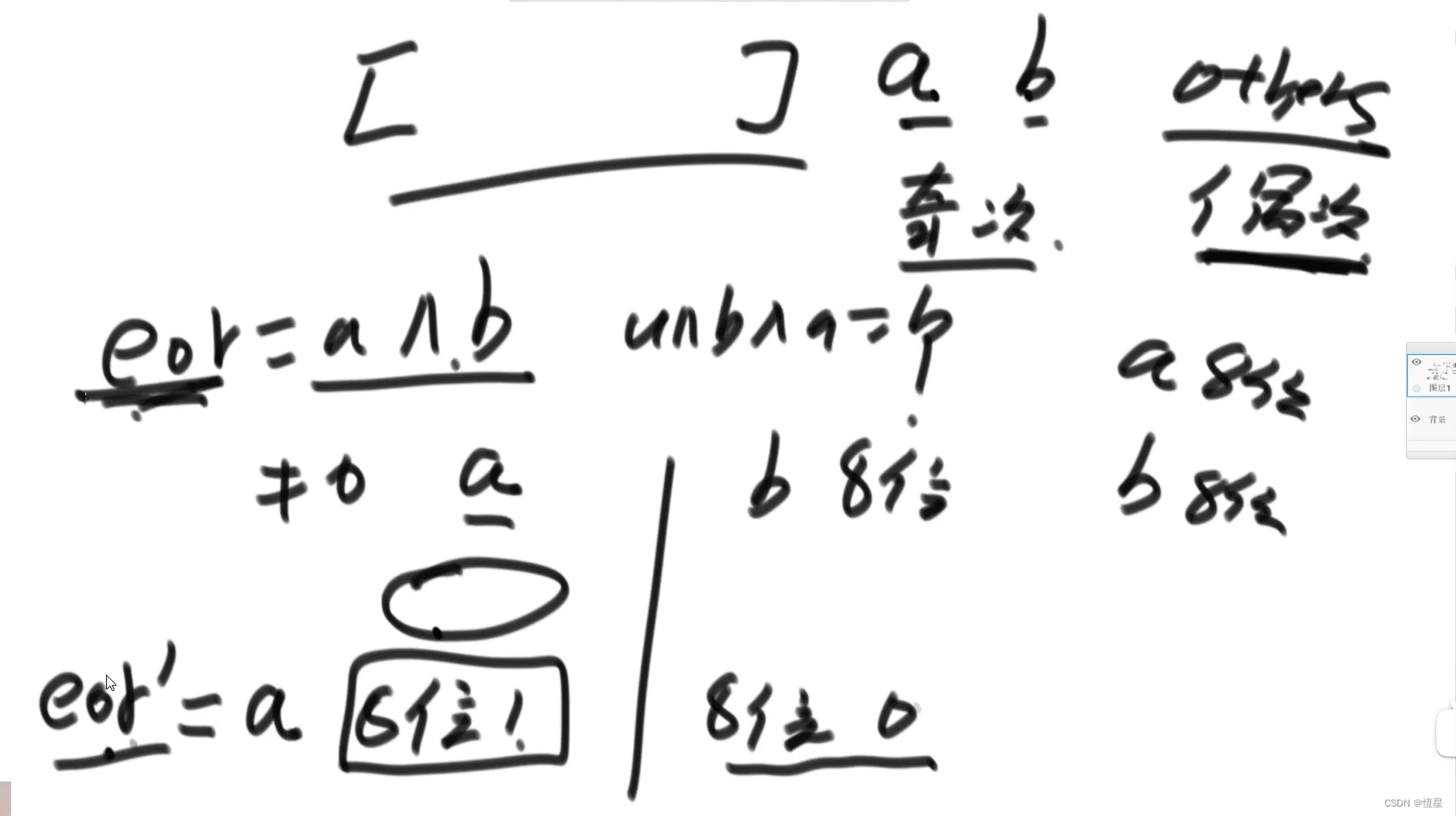

提取最右侧的1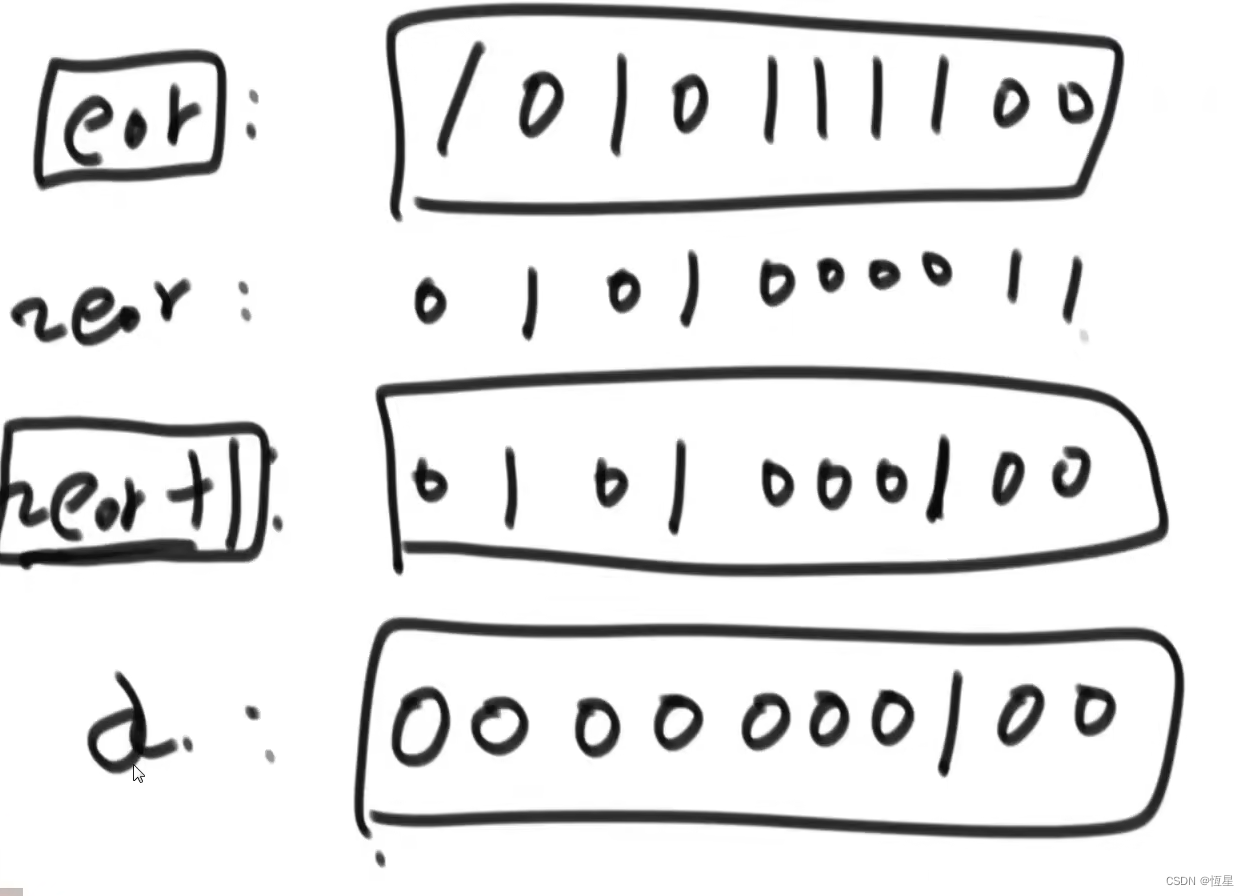

第二问代码

public static void printOddTimesNum2(int[] arr){
    int eor = 0;
    for (int cur:arr) {
        eor ^= cur;     //eor = a^b
    }
    int rightOne = (~eor + 1) & eor;    //提取最右侧的1
    int onlyOne = 0;        //eor'
    for(int cur : arr){
        if((cur & rightOne) == 0){
            onlyOne ^= cur;         //eor'=a|b
        }
    }

    System.out.println(onlyOne+"  "+(eor^onlyOne));

}

插入排序

比冒泡和选择要快，这两个一直都是O(n²)，而插入最差O(n²)，最好Ω(n)。

public static void insertionSort(int[] arr){
    if(arr == null || arr.length < 2){
        return;
    }
    for(int i = 1; i < arr.length; i++){
        for(int j = i-1; j >= 0 && arr[j] > arr[j+1]; j--){
            swap(arr, j, j+1);
        }
    }
}

public static void swap(int[] arr, i, j){ //投机解法，详见异或运算实例
    arr[i] = arr[i] ^ arr[j];
    arr[j] = arr[i] ^ arr[j];
    arr[i] = arr[i] ^ arr[j];
}

二分法

时间复杂度O(log₂N)

用途：

1. 寻找数组中的一个数

2. 寻找大于或小于某数的最左侧或最右侧的数的位置

并不是只有有序数列才可以二分，特定问题的无序数列也可以。例如找局部最小值。

对数器

递归

例题：用递归方法找一个数组中的最大值

public static int process(int[] arr, int l, int r){
    if(l == r){
        return arr[l];
    }
    int mid = l + ((r-l)>>1);
    int leftMax = process(arr, l, mid);
    int rightMax = process(arr, mid+1, r);
    return Math.max(leftMax, rightMax)
}

public static int getMax(int[] arr){
    return process(arr, 0, arr.length-1);
}

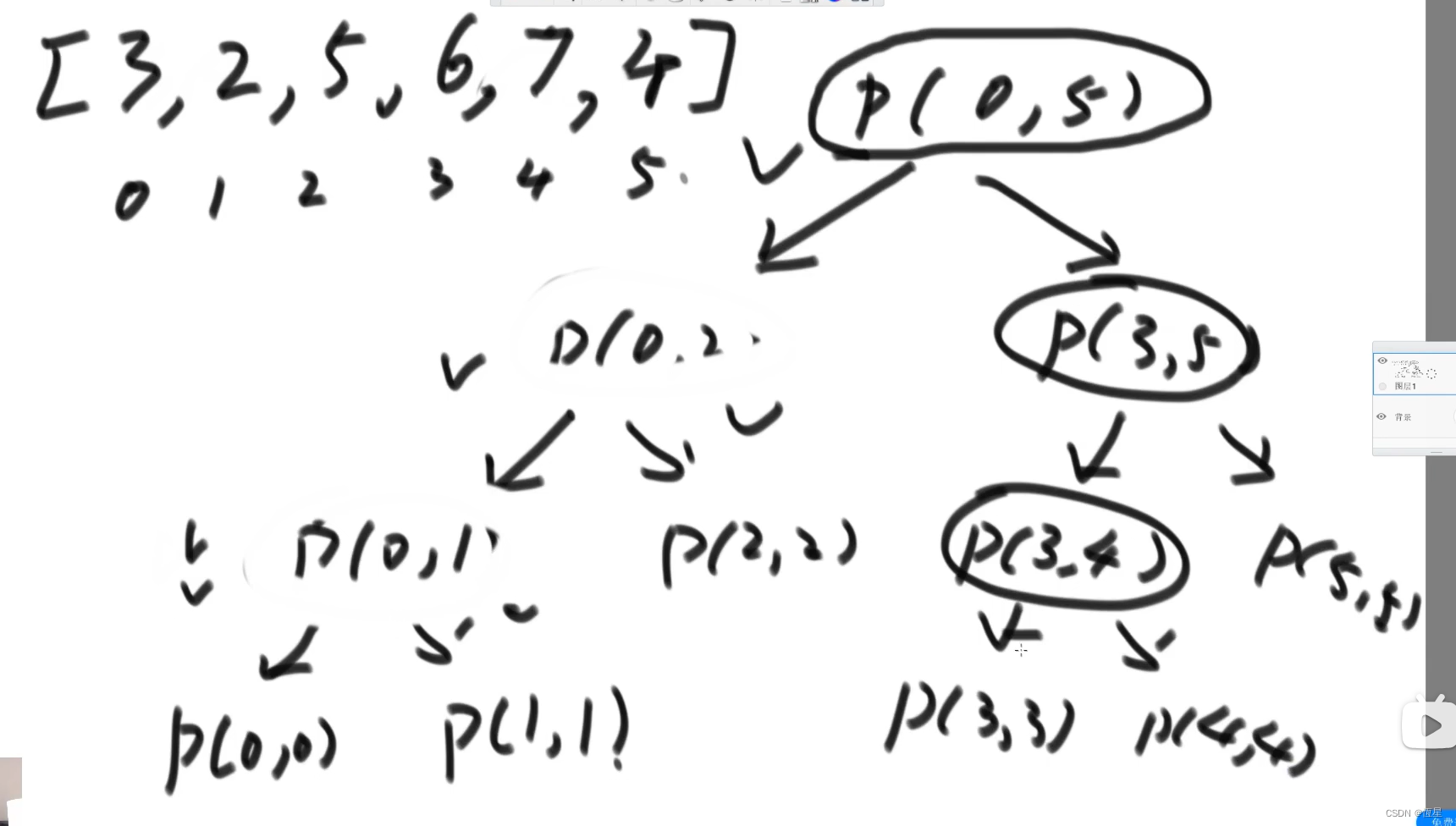
master公式

条件：满足子问题等规模的递归
$$T(N)=a\ast T(\frac{N}{b})+O(N^d)$$

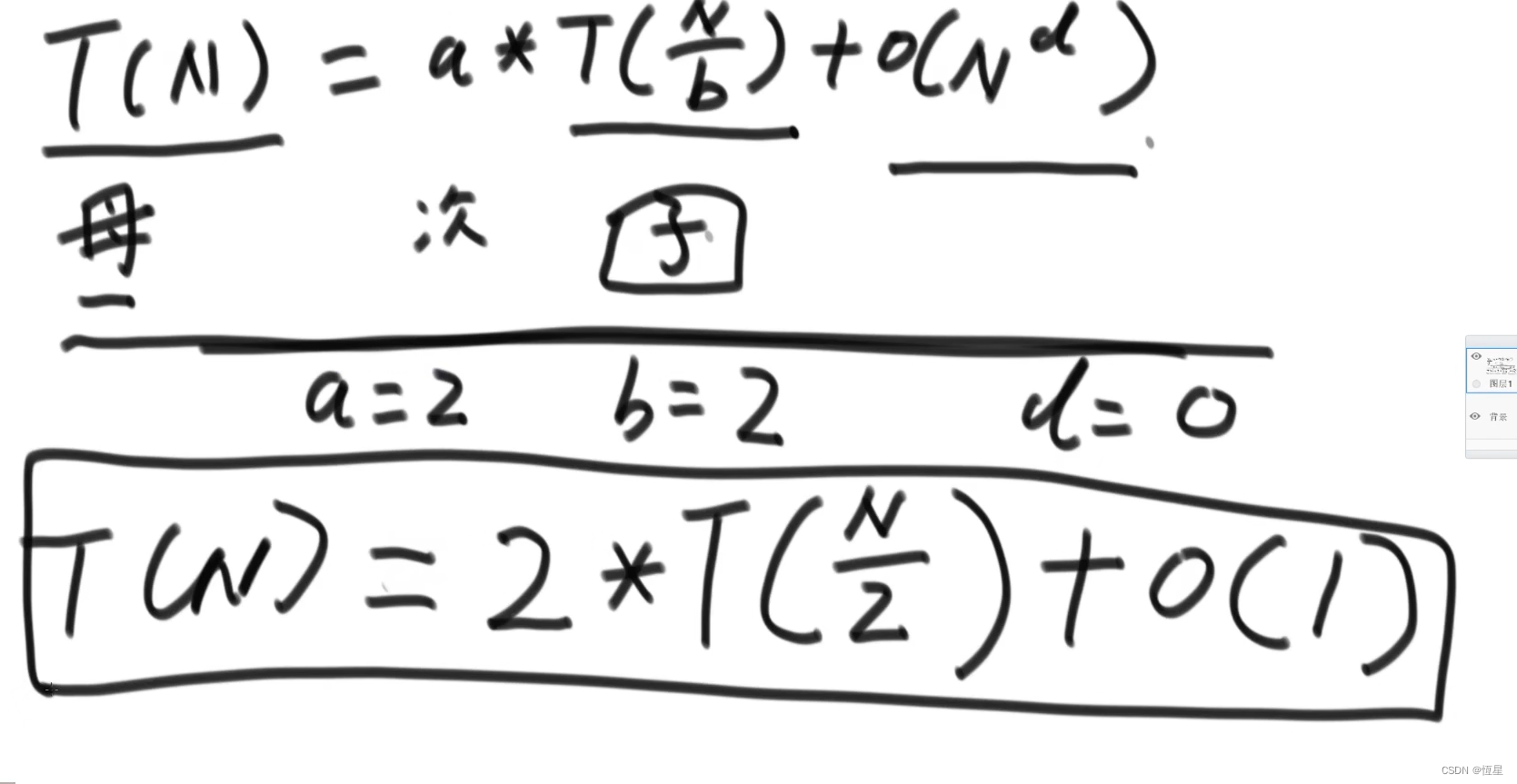
利用master公式算时间复杂度

$$1)lo{g}_{b}a>d\to 复杂度为O(N^{lo{g}_{b}a})$$

$$2)lo{g}_{b}a<d\to 复杂度为O(N^d)$$

$$3)lo{g}_{b}a=d\to 复杂度为O(N^d\ast lo{g}_{2}N)$$