哈夫曼树简介

        哈夫曼树，又称为最优二叉树，是一种带权路径长度最短的二叉树。在哈夫曼树中，每个节点都被赋予一个具有实际意义的实数，称为节点的权。带权路径长度（WPL）是从根节点到某一节点的路径长度与该节点权的乘积。而树的带权路径长度则是根到所有叶子节点的各个带权路径长度之和。

哈夫曼树相关的几个名词

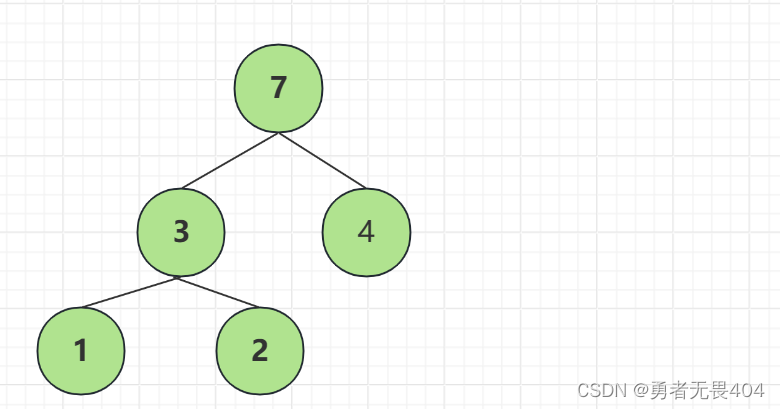
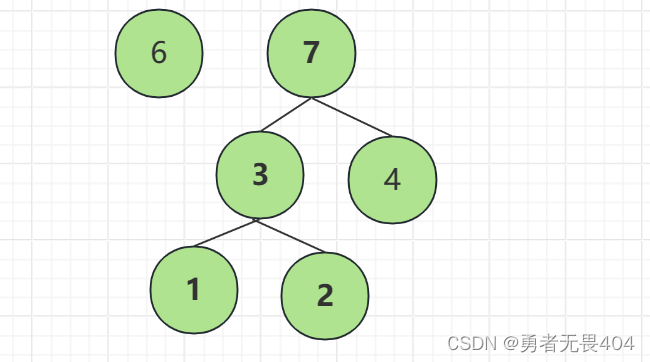
路径：在一棵树中从一个节点到另一个节点的通路，称为路径。如图从节点7到节点4之间的通路就是一条路径

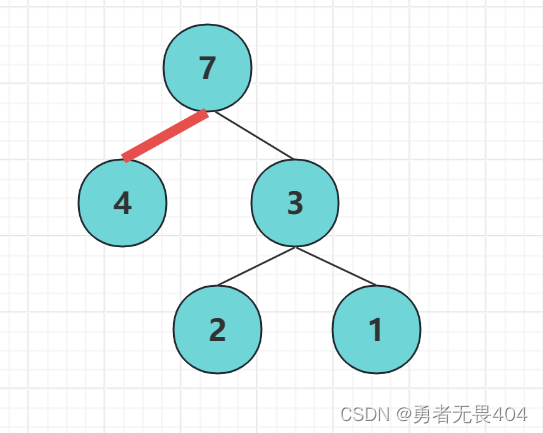
 路径长度：在一条路径中，每经过一个节点，路径长度都要加1。例如从节点7到节点1的路径长度为2

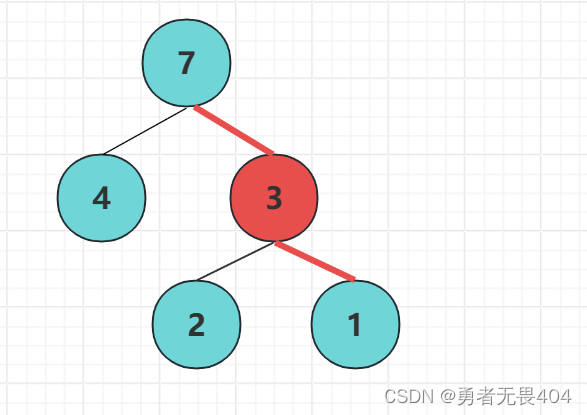
 节点的权：每个节点赋予一个值称为该节点的权值。节点7的权值为7，节点1的权值为1

节点的带权路径长度：从根节点到该节点之间的长度与该节点的权的乘积。如图根节点到节点2的带权路径长度为2*2=4

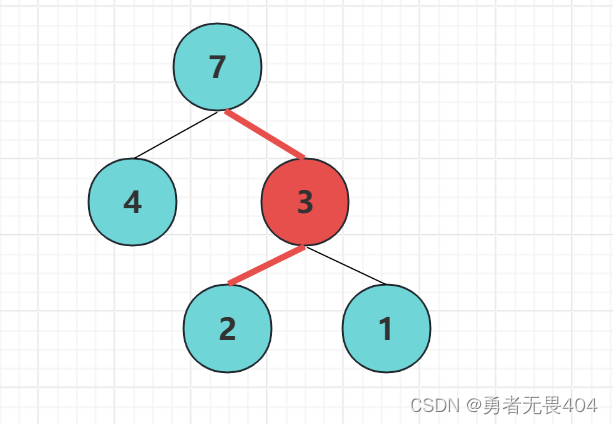
 树的带权路径长度：树中所有叶子结点的带权路径长度之和。通常记作 “WPL”。图中这棵树的带权路径长度为：2*1+2*2+4*1=10

 哈夫曼树的特点

当用n个带权值的叶子节点构建一棵二叉树，如果这棵二叉树的带权路径长度最小，称这棵树为最优二叉树或哈夫曼树，因此在构建哈夫曼树应遵循权值越大的节点离根节点越近。

哈夫曼树的构建

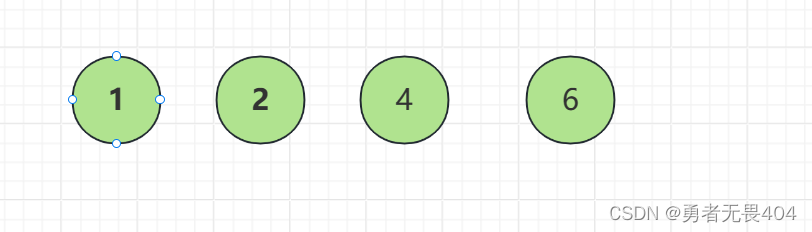
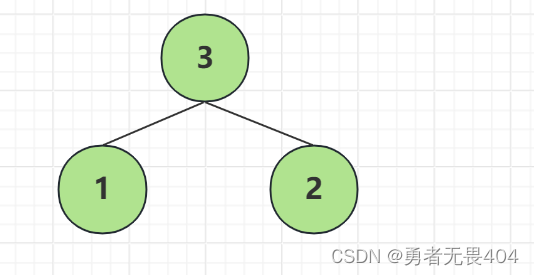
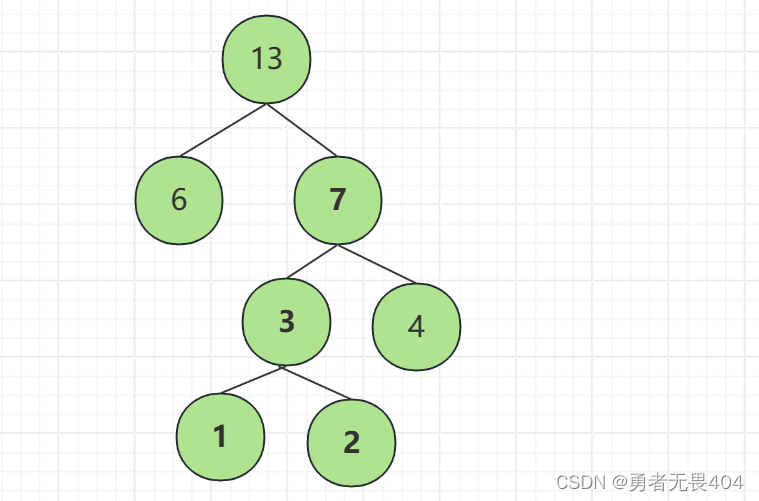
1.在n个带权节点中选出两个最小的节点，将其组成一个新的二叉树，且新二叉树的根节点的权值为左右子节点的权值和。

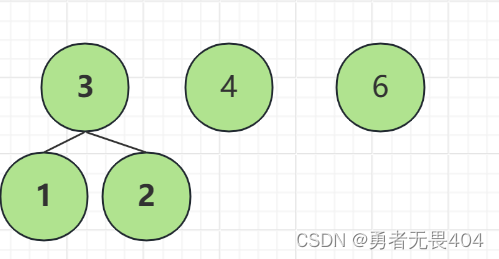
2.在n个带权节点中移除那两个最小的权值，同时将新的根节点加入。

3.重复1.2步骤直到只剩一个节点，则哈夫曼树构建完成。

 

 

 代码实现

/**
 * hfm tree
 *
 * @author haoge
 * @date 2024/04/25
 */
public class HfmTree {

    public static void main(String[] args) {
        List<Integer> list = Arrays.asList(9, 8, 7, 6, 5, 4, 3, 2, 1);
        PriorityQueue<TreeNode> queue = new PriorityQueue<>();
        for (Integer integer : list) {
            queue.offer(new TreeNode(integer));
        }
        while (queue.size() > 1) {
            TreeNode left = queue.poll();
            TreeNode right = queue.poll();
            TreeNode root = new TreeNode(left.weight + right.weight);
            root.left = left;
            root.right = right;
            queue.offer(root);
        }
        TreeNode root = queue.poll();
        print(root,0);
    }

    public static void print(TreeNode root,int level) {
        if (root == null) {
            return;
        }
        System.out.println(getIndentation(level)+root.weight);
        print(root.left,level+1);
        print(root.right,level+1);

    }

    public static String getIndentation(int level) {
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < level; i++) {
            sb.append("    ");
        }
        return sb.toString();
    }
}
class TreeNode implements Comparable<TreeNode>{
    int weight;
    TreeNode left;
    TreeNode right;

    public TreeNode() {

    }

    public TreeNode(int weight) {
        this.weight = weight;
    }

    @Override
    public int compareTo(TreeNode o) {
        return this.weight-o.weight;
    }
}

运行结果：

 哈夫曼树应用——哈夫曼编码

        哈夫曼编码的基本思想是以字符的使用频率作为权值构建一颗哈夫曼树，然后利用哈夫曼树对字符进行编码。

/**
 * hfm code
 *
 * @author haoge
 * @date 2024/04/25
 */
public class HfmCode {
    public static Map<Character, String> MAP = new HashMap<>();
    public static TreeNode buildHuffmanTree(Map<Character, Integer> map) {
        PriorityQueue<TreeNode> queue = new PriorityQueue<>();
        for (Map.Entry<Character, Integer> entry : map.entrySet()) {
            queue.offer(new TreeNode(entry.getValue(), entry.getKey()));
        }
        while (queue.size() > 1) {
            TreeNode left = queue.poll();
            TreeNode right = queue.poll();
            TreeNode root = new TreeNode(left.weight + right.weight, '$');
            root.left = left;
            root.right = right;
            queue.offer(root);
        }
        return queue.poll();
    }
    public static void getCodes(TreeNode root, String str, Map<Character, String> map) {
        if (root.left == null && root.right == null) {
            map.put(root.data, str);
            return;
        }
        getCodes(root.left, str + "0", map);
        getCodes(root.right, str + "1", map);
    }
    public static void main(String[] args) {
        String str = "this is an example for huffman encoding";
        Map<Character, Integer> map = new HashMap<>();
        for (char c : str.toCharArray()) {
            map.put(c, map.getOrDefault(c, 0) + 1);
        }
        TreeNode root = buildHuffmanTree(map);
        getCodes(root,"",MAP);
        for (Map.Entry<Character, String> entry : MAP.entrySet()) {
            System.out.println(entry.getKey() + "\t" + entry.getValue());
        }
    }
}
class TreeNode implements Comparable<TreeNode>{
    int weight;
    char data;
    TreeNode left,right;

    public TreeNode() {

    }
    public TreeNode(int weight, char data) {
        this.weight = weight;
        this.data = data;
    }
    @Override
    public int compareTo(TreeNode o) {
        return this.weight-o.weight;
    }
}

 哈夫曼编码通常用来进行数据压缩