——本节内容为Bilibili王道考研《数据结构》P49视频内容笔记。

---

目录

一、树的存储结构

1.双亲表示法（顺序存储）

2.孩子表示法（顺序+链式存储）

3.孩子兄弟表示法（链式存储）

4.森林和二叉树的转换

---

一、树的存储结构

1.双亲表示法（顺序存储）

（1）定义：每个结点中保存指向双亲的“指针”（实则为数组下标）；

（2）图示：

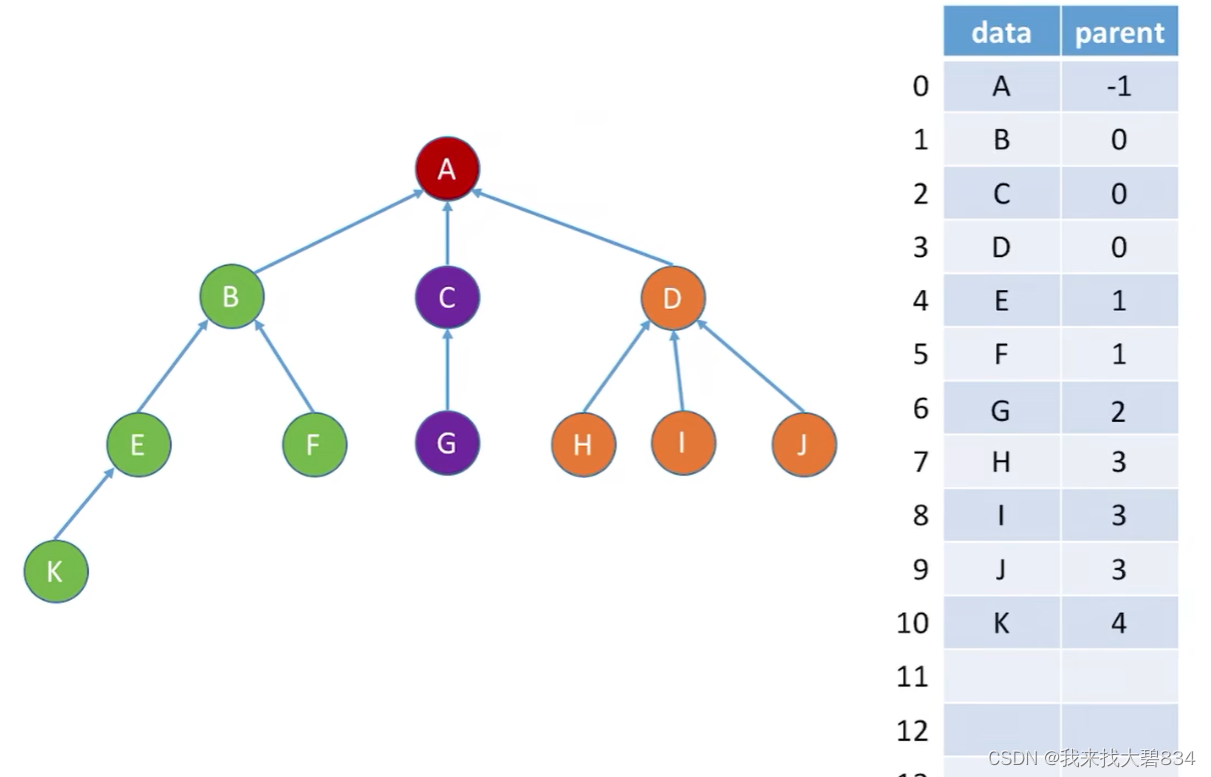
（3）代码实现：

#define MAX_TREE_SIZE 100			//树中最多结点数
typedef struct {					//树的结点定义
	char data;						//数据元素
	int parent;						//双亲位置域
}PTNode;

typedef struct {					//树的类型定义
	PTNode nodes[MAX_TREE_SIZE];	//双亲表示
	int n;							//结点数
}PTree;

（4）补充说明：

①采用数组的形式，把根结点固定存在数组下标为0的位置，并且用-1表示其没有父结点；

②不需要一定按照层序遍历的顺序去排列，物理上可以乱序；

（5）增加：写入增加元素的值，并记录与双亲的关系即可；

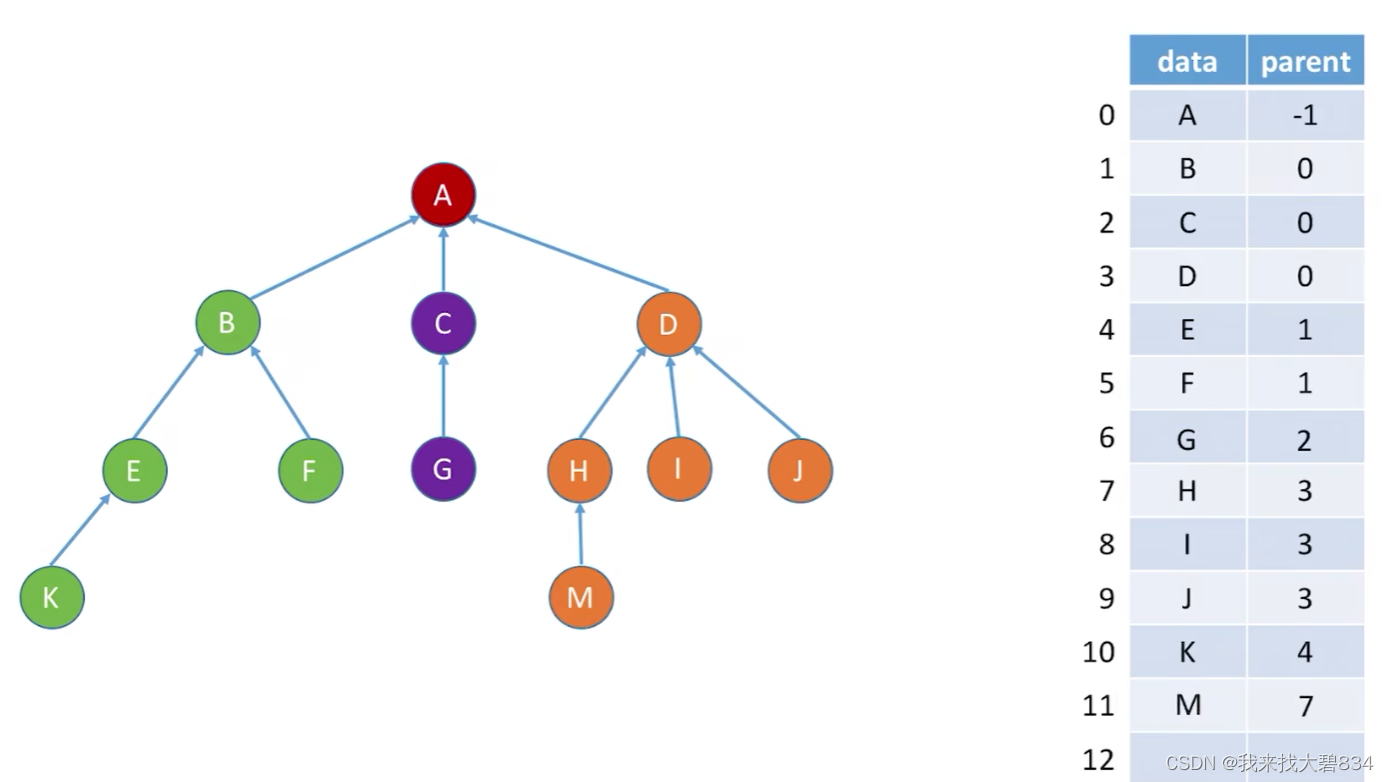
（6）删除：

①把所删除的结点的双亲指针设为-1，表明这个位置已空；最后给结点数n--；

②可以把尾部数据移动上来来填充前面要删除的元素，最后给结点数n--；

③ 方法②优于方法①；

④如果删除的结点是一棵子树的根结点，那么要将这棵子树的所有结点都删掉；此时需要找到孩子结点，即用到查询操作；

（7）查询：双亲表示法来查指定结点的双亲很方便，但查找孩子结点只能从头到尾遍历依次对比；

---

2.孩子表示法（顺序+链式存储）

（1）定义：顺序存储各个结点，每个结点中保存孩子链表头指针；

（2）图示：

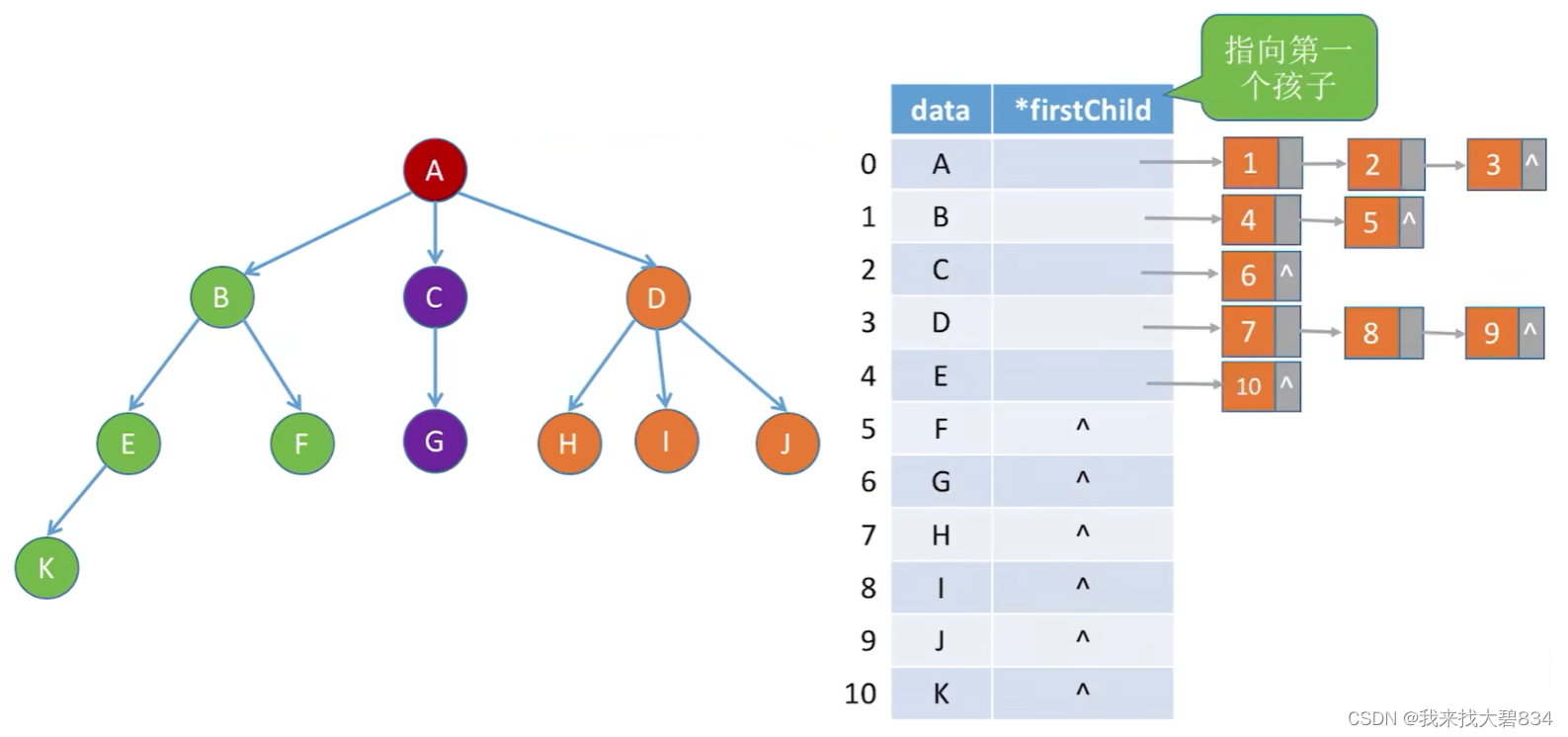
 （3）代码实现：

struct CTNode {
	int child;						//孩子结点在数组中的位置
	struct CTNode* next;			//下一个孩子
};

typedef struct {
	char data;
	struct CTNode* firstchild;		//第一个孩子
}CTBox;

typedef struct {
	CTBox nodes[MAX_TREE_SIZE];
	int n, r;						//结点数和根的位置
}CTree;

（4）补充解释：

①各个结点实际的数据使用CTBox来存储的；

②链表中的结点CTNode只是保存了各个孩子的数组下标；

---

3.孩子兄弟表示法（链式存储）

（1）代码实现：

typedef struct CSNode {
	char data;
	struct CSNode* firstchild, * nextsibling;
};

（2）解释说明：

①这种链式存储和二叉链表相似；

②我们可以把*firstchild看成*lchild；把*nextsibling看成*rchild；

③孩子结点就当左孩子结点，兄弟结点就当右孩子结点；

④我们可以用熟悉的二叉树操作来处理；

（3）图示：

 

 

---

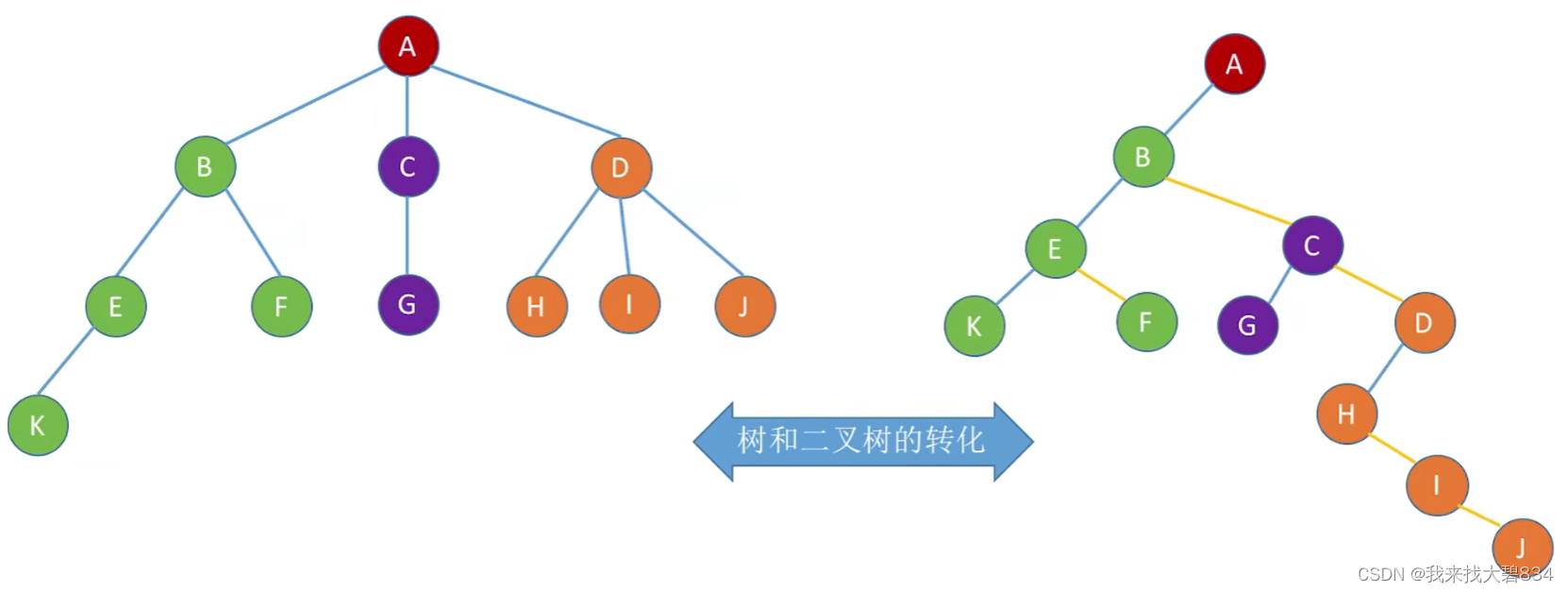
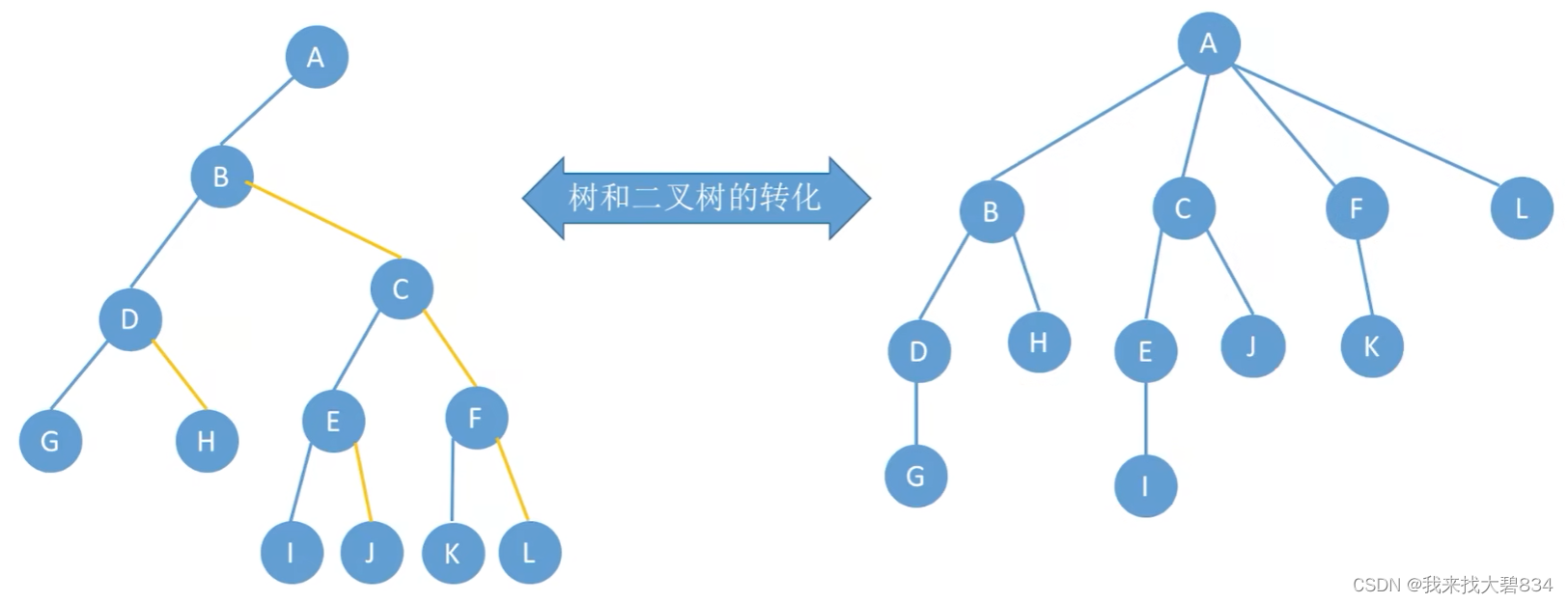
4.森林和二叉树的转换

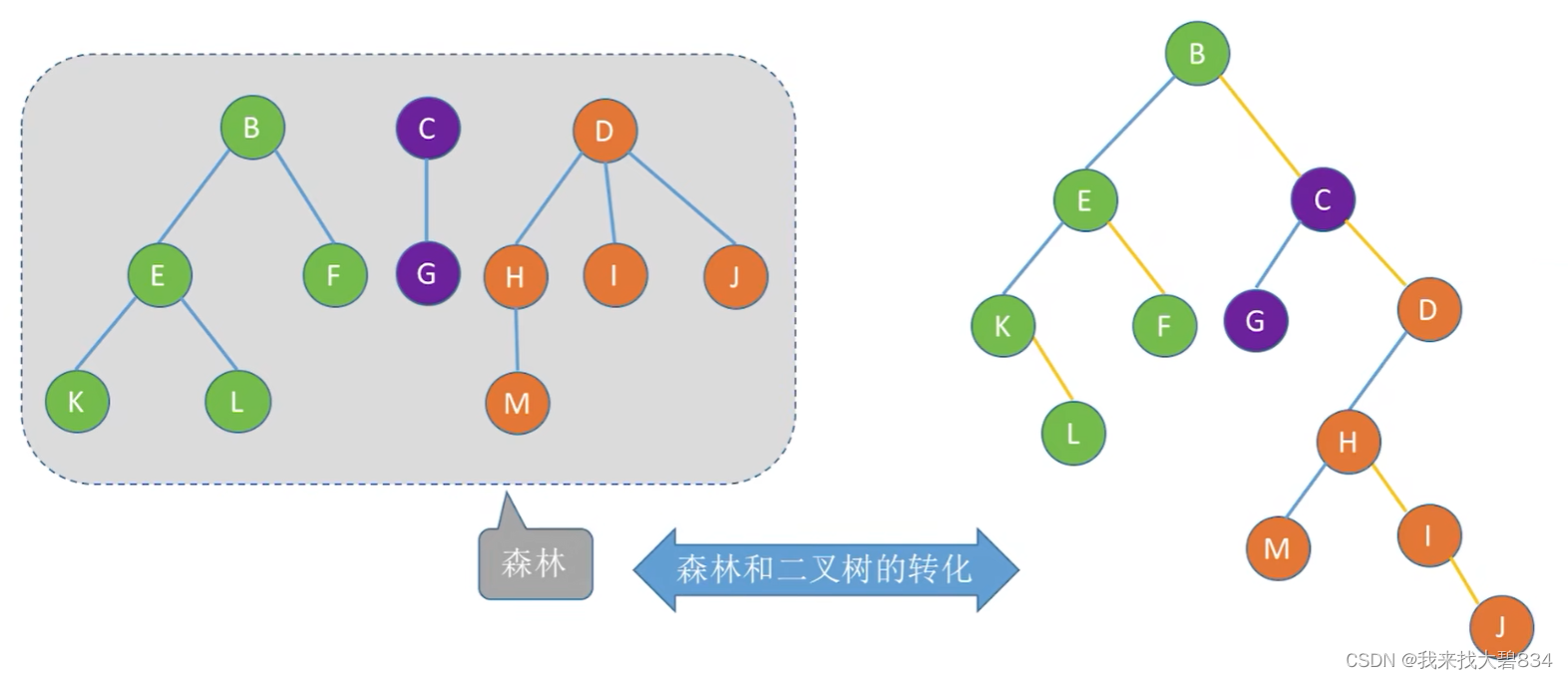
（1）森林转换二叉树：

先将森林的各个树转换为二叉树，再将各个树的根结点视为兄弟关系绑在一起即可；如图所示：

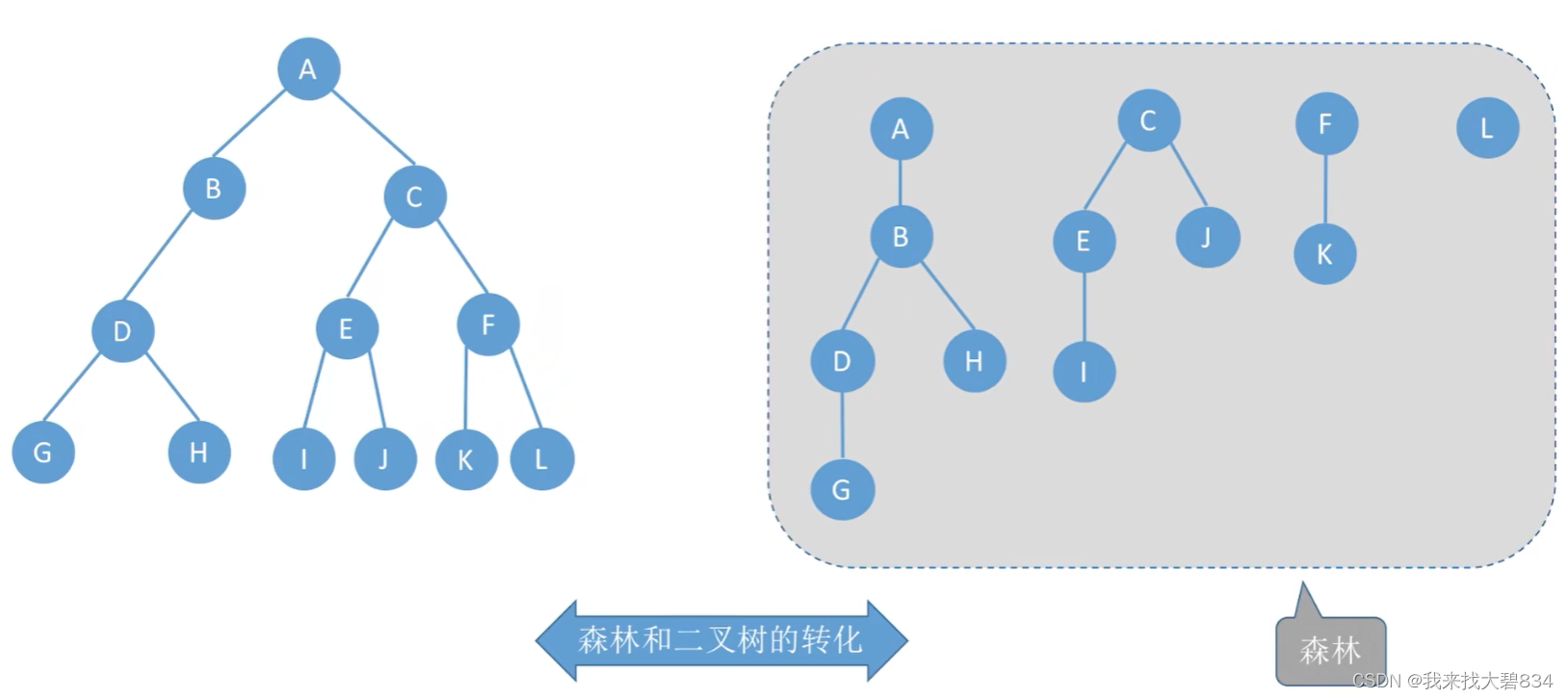
（2）二叉树转换森林：

左边为孩子，右边为兄弟，最右边一条线上的为各个树的根结点；如图所示：