数据结构考研第五章——树与二叉树（内含动图）

数据结构、考研、第五章、树与二叉树、内含动图、总结、笔记

后端漫漫

1470人浏览 · 2022-11-08 20:46:14

后端漫漫 · 2022-11-08 20:46:14 发布

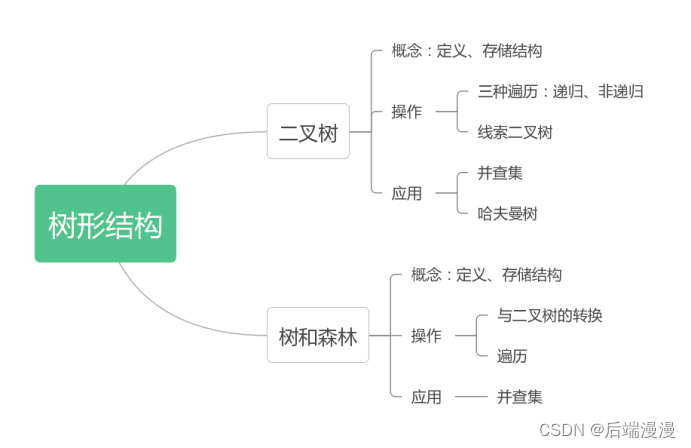
在这里插入图片描述

一、树的基本概念

基本术语

结点的度：一个结点的孩子个数称为结点的度
树的度：树中结点的最大度数称为树的度

分支结点：度大于0的结点
叶子结点：度等于0的结点

结点的深度：从根结点开始自上而下逐层累加的
结点的高度：从叶子结点开始自底向上逐层累加的

有序树：树中各结点从左到右是有次序的，不能互换，互换后会变成另一棵不同的树
无序树：树中各结点从左到右是无次序的，可以互换，互换后会变成另一棵不同的树

路径：两个结点之间的路径是由这两个结点之间所经过的结点序列构成的
路径长度：路径上所经过的边的个数

树的性质（结点数、高度）

树中的结点数等于所有结点的度数加1；（除了根结点，每个结点头上都插着一个针）

度为m的树中第i层上至多有 $m^{i-1}$ 个结点

高度为h的m叉树至多有 $m^h-1)$ / $(m - 1)$ 个结点

具有n个结点的m叉树的最小高度为math.ceil[ $log_m$ (n(m-1) +1) ]

二、二叉树的基本概念

特殊二叉树

满二叉树
完全二叉树
二叉排序树
平衡二叉树

二叉树的性质（结点数、高度、编号、链域）

树中的结点数等于所有结点的度数加1；（除了根结点，每个结点头上都插着一个针）；

非空叉树的叶子结点数等于度为2的结点数加1；

高度为h的m叉树至多有 $2^h-1)$ 个结点；

度为m的树中第i层上至多有 $2^{i-1}$ 个结点；

具有n个结点的m叉树的最小高度为math.ceil[ $log_2$ (n+1)

结点i的双亲编号：i/2;
结点i的左孩子编号：2i；
结点的右孩子编号：2i+1；

链式存储结构：在含n个结点的二叉链表中，含有n+1个空链域

二叉树的存储结构

【顺序存储结构】（从1开始存储）

适用范围：完全二叉树和满二叉树

数组下标：使用数组存储二叉树，建议从数组下标1开始存储树中的结点，若从数组下标0开始存储，则不满足性质4的描述。

【链式存储结构】 （在含n个结点的二叉链表中，含有n+1个空链域）

typedef struct BiTNode{
	ElemType data;
	struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

三、二叉树的遍历

注意：二叉树的先序中序后序遍历就是深度优先遍历。

先序遍历

【递归先序遍历】

void PreOrder(BiTree T){
	visit(T);
	PreOrder(T->lchild);
	PreOrder(T->rchild);
}

【非递归先序遍历】

//结点不为空就visit&push&lchild，结点为空就Pop&rchild，总结为vpl&pr
int PreOrder(BiTree T){
	if(T==NULL) return;
	
	SqStack S;
	InitStack(&S);
	BiTree p=T;
	while(p||!StackEmpty(S)){
		while(p){						
			visit(p);
			Push(&S,*p);
			p=p->lchild;
		}
		if(!StackEmpty(S)){
			Pop(&S,p);
			p=p->rchild;
		}
	}
	return 1;
}

中序遍历

【递归中序遍历】

void MidOrder(BiTree T){
	PreOrder(T->lchild);
	visit(T);
	PreOrder(T->rchild);
}

【非递归中序遍历】

//结点不为空就push&lchild，结点为空就Pop&visit&rchild，总结为pl&pvr
void MidOrder(BiTree T){
	if(T==NULL) return;

	InitStack(S);
	BiTree p=T;
	while(p||!StackEmpty(S)){
		while(p){
			Push(p);
			p=p->lchild;
		}
		if(!StackEmpty(S)){
			Pop(S,p);
			visit(p);
			p=p->rchild;
		}
	}
}

后序遍历

【递归后序遍历】

void PreOrder(BiTree T){
	PreOrder(T->lchild);
	PreOrder(T->rchild);
	visit(T);
}

【非递归后序遍历】

//结点不为空就push&lchild，结点为空就Pop&visit&rchild，总结为pl&pprv
void PostOrder(BiTree T){
	if(T==NULL) return;    //重点呀大哥
	
	InitStack S;
	BiTree p;
	p.ptr=T;
	p.tag=0;
	Push(S,p);

	while(!p||StackEmpty(S)){
		while(p){
			Push(S,p);
			p=p->lchild;
		}
		if(!StackEmpty(S)){
			Pop(S,p);
			if(!p->tag){
				p->tag++;
				Push(S,p);
			}
			if(p->rchild) p=p->rchild;
			else visit(p);
		}
	}
}

层次遍历

【借助队列实现】

void LevelOrder(BiTree T){
	if(T==NULL) return;

	InitQueue(Q);
	BiTree p;
	EnQueue(Q,p);
	while(p||!QueueEmpty(Q)){
		DeQueue(Q,p);
		visit(p);
		if(p=p->lchild!=NULL) EnQueue(Q,p->lchild);
		if(p=p->rchild!=NULL) EnQueQue(Q,p->rchild);
	}
}

由遍历序列构造二叉树

由二叉树的先序序列和中序序列可以唯一地确定一棵二叉树。

四、线索二叉树

线索二叉树的定义

遍历二叉树是以一定的规则将二叉树中的结点排列成一个线性序列，从而得到几种遍历序列，使得该序列中的每个结点都有一个直接前驱和直接后继。

typedef struct ThreadNode{
	ElemType data;
	struct ThreadNode *lchild,*rchild;	//指示左右孩子，或者指示前驱后继
	int ltag,rtag;						//tag为0时指示左右孩子，tag为1时指示前驱后继
}ThreadNode,*ThreadTree;

在这里插入图片描述

二叉树的线索化

【共用模块】

void visit(ThreadNode *q){
	if(q->lchild==NULL){
		q->lchild=pre;	//左子树指向了前驱
		q->ltag=1;
	}
	if(pre!=NULL&&pre->rchild==NULL){
		pre->rchild=q;	
		pre->rtag=1;
	}
	pre=q;	//pre是前结点，供后继结点q=lchild使用
}

【先序遍历线索化】

void PreThread(ThreadTree T){
	if(T==NULL) return;
    visit(T);		//pre变化顺序为根、左、右
    if(T->ltag==0) PreThread(T->lchild);	 
    PreThread(T->rchild);
}

void CreatePreThread(ThreadTree T){
    pre=NULL;
    if(T==NULL) return;
    PreThread(T);
    if(pre->rchild==NULL) pre->rtag=1;
}

【中序遍历线索化】

void InThread(ThreadTree T){
    if(T==NULL) return;
    InThread(T->lchild);
    visit(T);
    InThread(T->rchild);
}
 
void CreateInThread(ThreadTree T){
    pre=NULL;
    if(T==NULL) return;
    InThread(T);
    if(pre->rchild==NULL) pre->rtag=1;
}

【后序遍历线索化】

void PostThread(ThreadTree T){
    if(T!=NULL) return;
    PostThread(T->lchild);
    PostThread(T->rchild);
    visit(T);
}
 
void CreatePostThread(ThreadTree T){
    pre=NULL;
    if(T!=NULL) return;
    PostThread(T);
    if(pre->rchild==NULL) pre->rtag=1;
}

中序线索二叉树的遍历

在中序线索二叉树中找结点后继的规律是：

若其右标记为“1”，则右链为线索，指示其后继；

否则遍历右子树中第一个访问的结点（右子树中最左下的结点）为其后继；

//若其右标记为“1”，则右链为线索，指示其后继；
ThreadNode *Firstnode(ThreadNode *p){
	while(p->ltag==0) p=p->lchild;
	return p;
}

//否则遍历右子树中第一个访问的结点（右子树中最左下的结点）为其后继
ThreadNode *Nextnode(ThreadNode *p){
	if(p->rtag==0) return Firstnode(p->rchild);	//右子树
	else return p->rchild;						//后继
}

//使用上述两个函数就可以完成中序遍历
void Inorder(ThreadNode *T){
	for(ThreadNode *p=Firstnode(T);p!=NULL;p=nextnode(p))	visit(p);
}

五、树、森林

树的存储结构

【双亲表示法】

typedef MAX_TREE_SIZE 100
typedef struct{
	ElemType data;
	int parent;
}PTNode;
typedef struct{
	PTNode nodes[MAX_TREE_SIZE];
	int n;
}PTree;

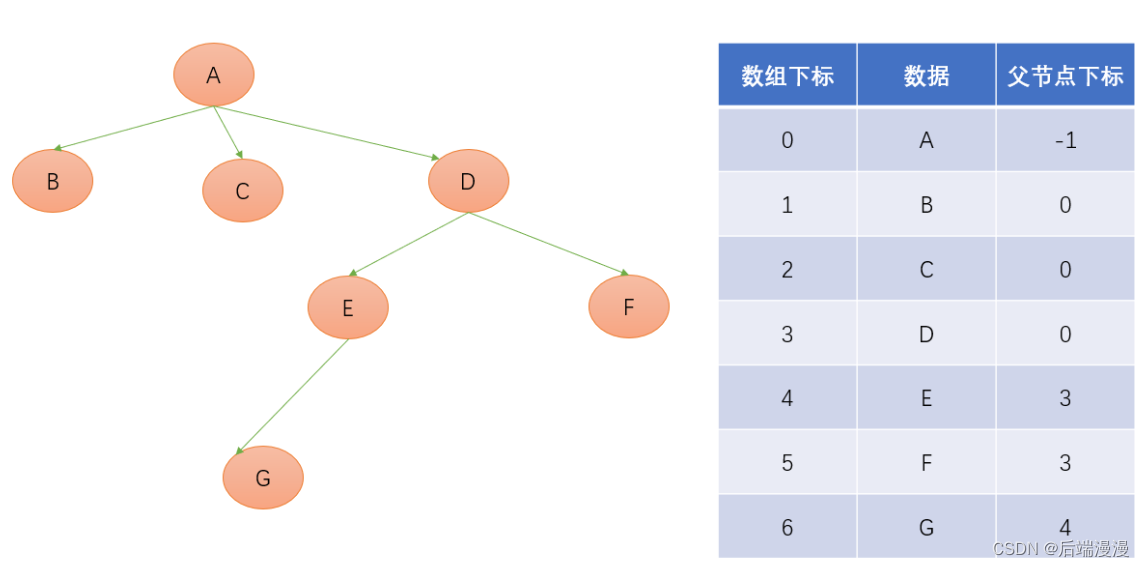
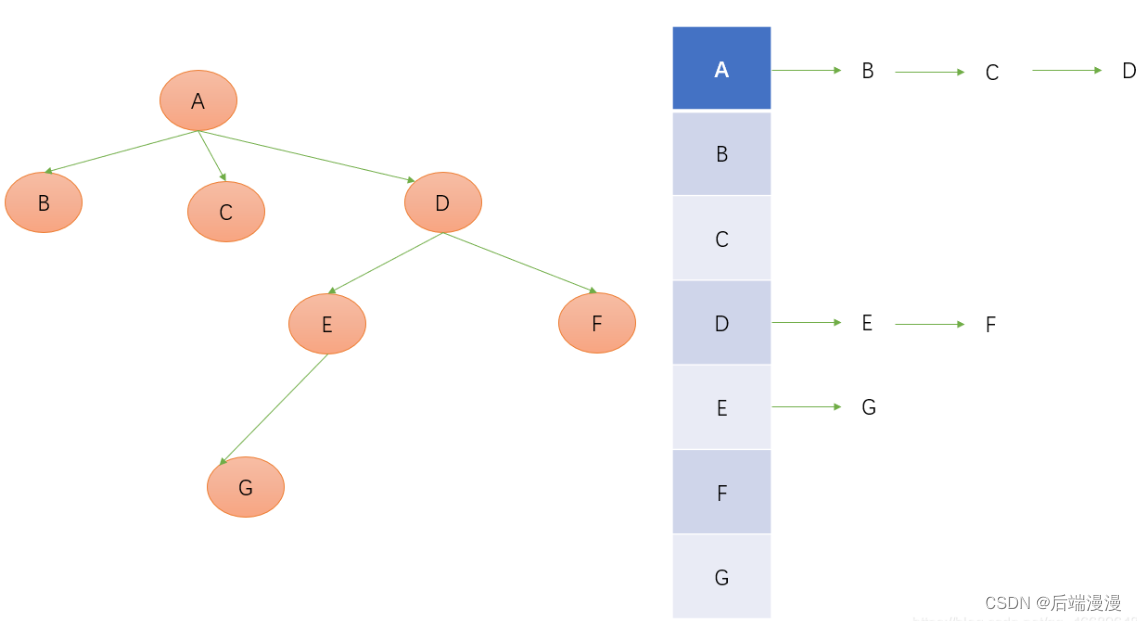
在这里插入图片描述

【孩子表示法】

将每个结点的孩子结点都用单链表链接起来形成一个线性结构，此时n个结点就有n个孩子链表。

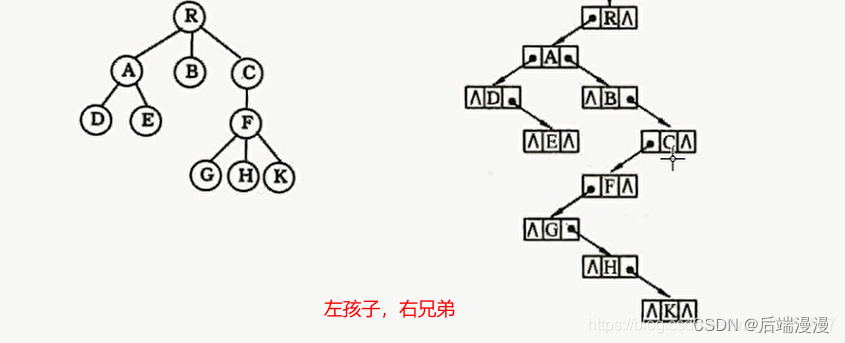
【孩子兄弟法】

typedef struct CSNode{
	ElemType data;
	struct CSNode *firstchild,*nextsibling;
}

在这里插入图片描述

树、森林与二叉树的转换
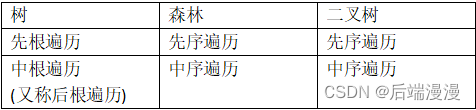
树和森林的遍历

六、哈夫曼树和哈夫曼编码

【基本概念】

带权路径长度WPL：树中所有叶结点的带权路径长度之和称为该树的带权路径长度

哈夫曼树：带权路径长度最小的二叉树称为哈夫曼树，也成为最优二叉树

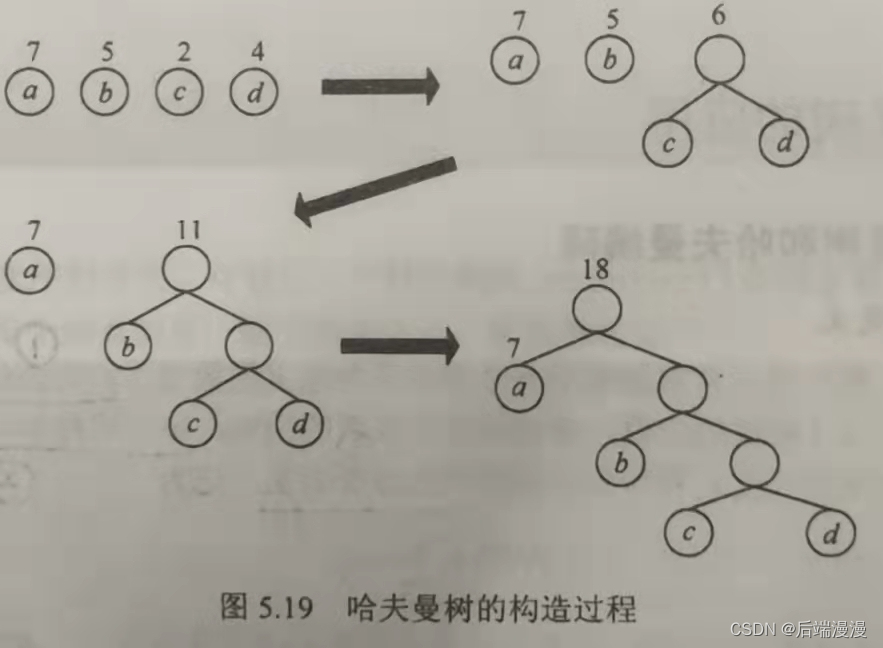
【哈夫曼树的构造】

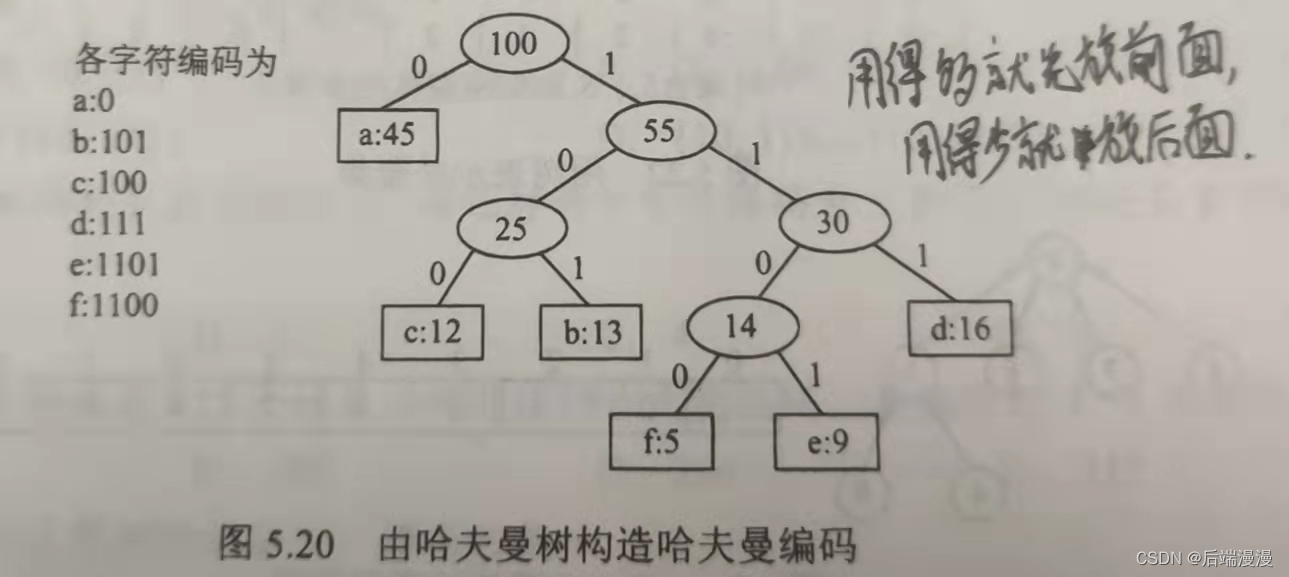
【哈夫曼编码】

七、并查集

存储结构 （下标为0的数组）
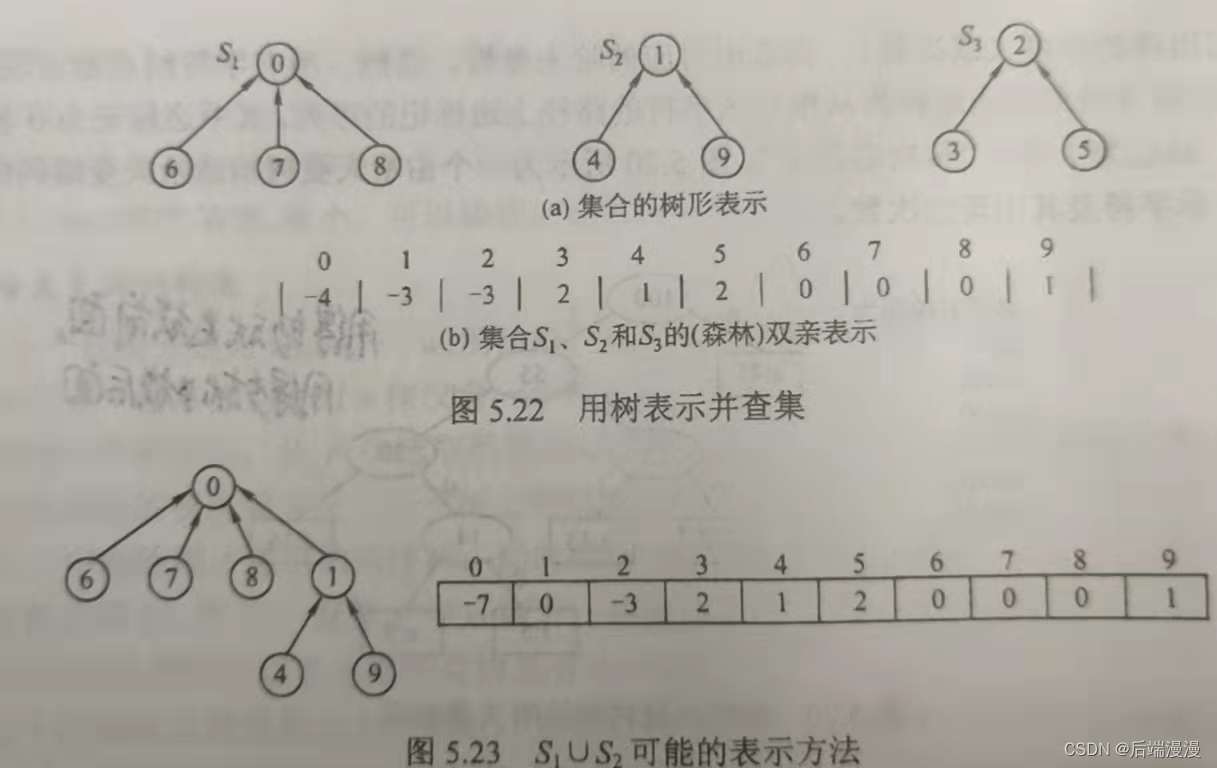
基本操作

【并查集的结构定义】

#define SIZE 100
int UFSets[SIZE];

【并查集初始化操作】

void Initial(int S[]){
	for(int i=0;i<size;i++) S[i]=-i;
}

【并查集查询操作】

int Find(int S[],int x){
	while(S[x]>=0) x=S[x];
	return x;
}

【并查集合并操作】

void Union(int S[],int Root1,int Root2){	//合并两个集合，必须先找到两个元素的根结点
	if(Root1==Root2) return;
	S[Root2]==S[Root1];
}

魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

【计算机视觉】Pixel逐像素分类&Mask掩码分类理解摘要

魔乐社区

计算机视觉（opencv）实战三十二——CascadeClassifier 人脸微笑检测（摄像头）

本文从原理到实现，详细介绍了基于 OpenCV Haar 分类器的人脸与微笑检测：讲解了 Haar 特征和级联检测原理。对代码逐行拆解并解释参数含义。画出完整流程图，帮助理解执行过程。给出了常见问题和优化建议，甚至扩展到深度学习方法。这种方法简单、轻量、实时性好，非常适合入门和小型应用项目。但如果需要更高准确率和更强鲁棒性，建议使用深度学习检测器替代 Haar 分类器。