1. 数组

在一段 连续的内存空间 存储多个 类型相同 的数据

2. 数组和线性表的区别

2.1 数组与顺序表的区别

（1）数组和顺序表都是在一段 连续的内存空间 存储多个 类型相同 的数据
（2）数组的长度不可改变，顺序表的长度是动态的，可进行增删改查。

2.2 数组与链表的区别

（1）数组静态分配内存，链表动态分配内存
（2）数组在内存中连续，链表可以连续，也可以不连续，一般是不连续的
（3）数组元素在栈区，链表元素在堆区
（4）数组利用下标定位，时间复杂度为O(1)，链表定位元素时间复杂度O(n)；
（5）数组插入或删除元素的时间复杂度O(n)，链表的时间复杂度O(1)。

3. 线性表

线性表是n个具有相同类型的数据元素的有限序列，除了头和尾之外，它的每一个元素都只有一个前驱元素和一个后驱元素。它包括顺序表和链表。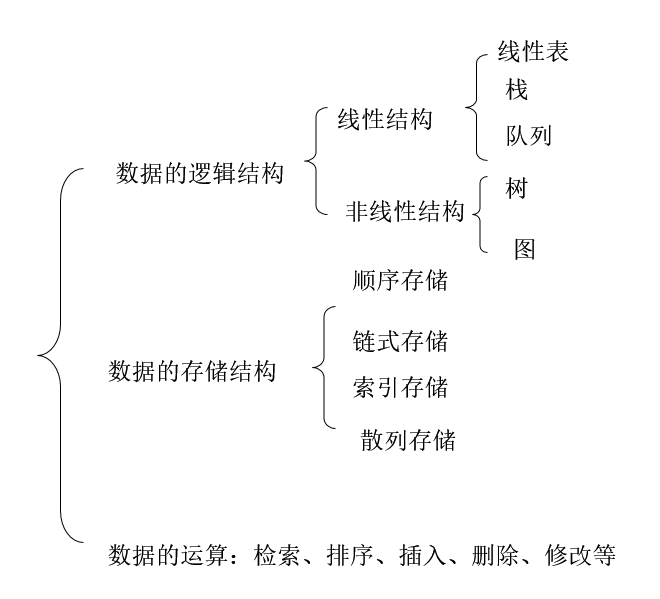

3.1 顺序表

线性表中的一种，它是用数组来实现的一种线性表，所以它的存储结构（物理结构）是连续的。

3.2 链表

线性表中的一种，它的存储结构是用任意一组存储单元来存储数据元素。所以它的存储结构可以是连续的，也可以不是连续的。一般我们说的链表都是不连续的。链表由一系列结点（链表中每一个元素称为结点）组成，每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域，采用指针链接的方式进行存储。

3.3 链表的插入和删除代码详解

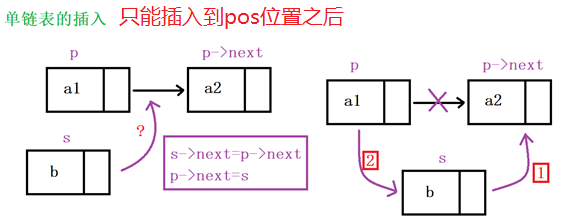
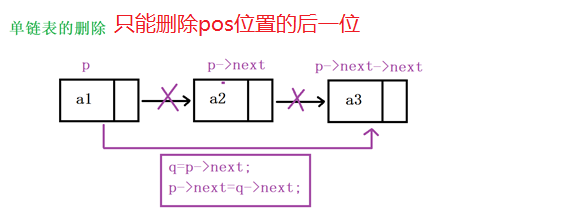
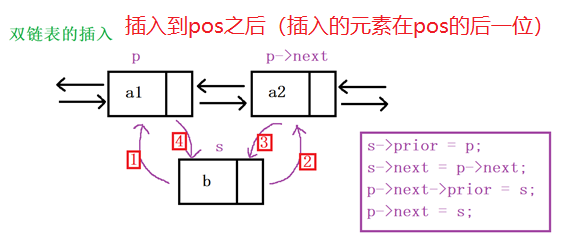
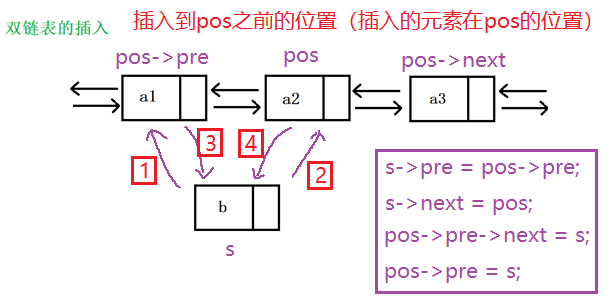
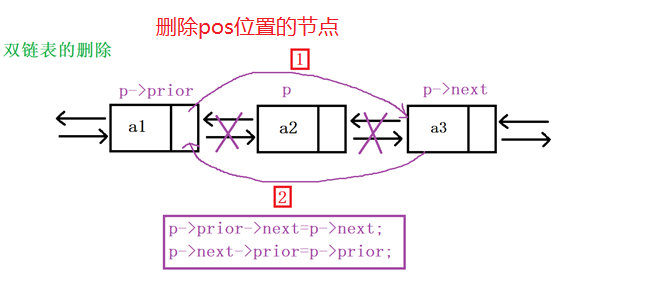
3.4 顺序表与链表的区别

首先，顺序表与链表均属于线性表，只是在逻辑结构和存储方式上有所不同。
顺序表：线性表采用顺序存储的方式存储就称之为顺序表，顺序表是将表中的结点依次存放在计算机内存中一组地址连续的存储单元中。
链表： 线性表采用指针链接的方式存储就称之为链表。
（1）在存储分配上：顺序表是用一段连续的内存空间依次存储数据元素。链表是用任意一组内存单元存放数据元素，采用指针链接的方式进行存储。
（2）时间性能上：顺序表的查找是O(1)，插入和删除需要搬移元素所以为O(N)。链表需要通过指针去一个一个查找所以查找是O(N)，而插入和删除比较方便为O(1)。
（3）空间性能上：顺序表需要预分配存储空间，分大了浪费，小了容易发生上溢。链表不需要分配存储空间，只要有就可以分配，元素个数不受限制。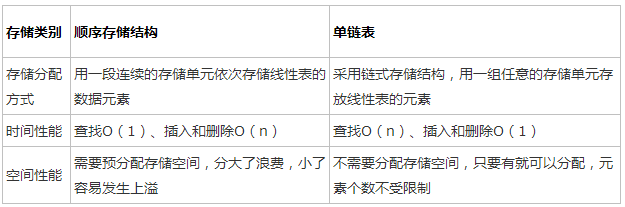

4. 栈

栈是一种特殊的线性数据结构，只能在其一端进行数据的插入和删除操作（即入栈和出栈），该端称为栈顶，另一端称为栈底。
遵循 “先进后出” 的原则。例如手枪弹夹，羽毛球桶。

栈的常用操作的模拟实现包括：初始化、入栈、出栈、获取元素个数、判空、获取栈顶元素。栈不能遍历。

栈的具体实现有以下两种方式：
顺序栈：采用顺序存储结构可以模拟栈存储数据的特点，从而实现栈存储结构；
链栈：采用链式存储结构实现栈结构；
两种实现方式的区别，仅限于数据元素在实际物理空间上存放的相对位置，顺序栈底层采用的是数组，链栈底层采用的是链表。

5. 队列

与栈结构不同的是，队列的两端都"开口"，要求数据只能从一端进，从另一端出，要遵循 “先进先出” 的原则。

顺序队列：用数组实现的队列
链式队列：用链表实现的队列
循环队列：队列前后连成一个圆圈，它以循环的方式去存储元素，但还是会按照队列的先进先出的原则去操作。循环队列是基于数组实现的队列，但它比普通数据实现的队列带来的好处是能更有效率的利用数组空间，且不需要移动数据。普通的数组队列在经过了一段时间的入队和出队以后，尾指针rear就指向了数组的最后位置了，没法再往队列里插入数据了，但是数组的前面部分（front的前面）由于旧的数据曾经出队了，所以会空出来一些空间，这些空间就没法利用起来。
优先队列：是一种特殊的队列，它不遵守先进先出的原则，它是按照优先级出队列的。分为最大优先队列（是指最大的元素优先出队）和最小优先队列（是指最小的元素优先出队）。一般用堆来实现优先队列。

6. 树

树是n(n>0)个结点的有限集。n=0时为空树。在任意一颗非空树中：(1)有且仅有一个根节点，(2)当n>1时，其余结点可分为m个互不相交的有限集，其中每一个集合本身又是一棵树，并且称为根的子树。

节点的度：一个节点所拥有的子树的个数
树的度：树内各节点的度的最大值
树的深度(高度)：树中节点的最大层次
父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
子节点：一个节点含有的子树的根节点称为该节点的子节点；
叶子节点(终端节点)：度为0的节点
森林：由m(m>=0)棵互不相交的树的集合称为森林

6.1 二叉树

每个节点最多含有两个子树且左右子树次序不能颠倒的树称为二叉树

性质1：在二叉树的第 i 层上最多有$2^{i-1}$个节点 (i>=1)。
性质2：二叉树中如果深度为k,那么最多有$2^k$ - 1个节点(k>=1)。
性质3：对于任意一棵二叉树，如果其叶子节点数为$N_0$，而度数为2的节点总数为$N_2$，则$N_0$=$N_2$+1;
性质4：具有n个结点的完全二叉树的深度为${log}_2$n + 1( log2n向下取整)
性质5：如果对一颗有n个节点的完全二叉树的节点按层序编号，对任一节点i：如果i=1，则节点i是二叉树的根；如果i>1，则其双亲是节点i/2；左孩子是节点2 * i；右孩子是节点2 * i + 1

6.2 满二叉树

在一棵二叉树中，如果所有分支节点都存在左子树和右子树，并且所有叶子节点都在同一层上，这样的二叉树称为满二叉树。

6.2 完全二叉树

对一颗具有n个节点的二叉树按层序编号，如果编号为i的节点与同样深度的满二叉树中编号为i的节点在二叉树中位置完全相同，则这颗二叉树成为完全二叉树

6.3 二叉查找树(二叉搜索树)

（1）若它的左子树不为空，则左子树上所有结点的值都小于根结点的值。
（2）若它的右子树不为空，则右子树上所有结点的值都大于根结点的值。
（3）它的左右子树也分别是二叉搜索树。

6.4 平衡二叉搜索树(AVL树)

（1）左子树与右子树高度之差的绝对值不超过1
（2）树的每个左子树和右子树都是AVL树
（3）每一个节点都有一个平衡因子（balance factor），任一节点的平衡因子是-1、0、1（每一个节点的平衡因子 = 右子树高度 - 左子树高度）

6.5 红黑树

1、每个节点不是红色就是黑色的。
2、根结点是黑色的。
3、每个叶节点是黑色的。
4、如果一个节点是红色的，则它的两个子节点都是黑色的。
5、对每个节点，从该节点到其所有后代叶结点的简单路径上，均包含相同数目的黑色节点。

7. 堆

堆的本质是一颗完全二叉树，是利用完全二叉树的结构来维护一组数据。分为大根堆和小根堆
大根堆：父节点的值大于或等于子节点的值；
小根堆：父节点的值小于或等于子节点的值。

8. 散列表（哈希表）

8.1 哈希表概念

散列表，又叫哈希表，散列表是一种空间换时间的存储结构，是能够通过给定的关键字的值直接访问到具体对应的值的一个数据结构。也就是说，把关键字映射到一个表中的位置来直接访问记录，以加快访问速度。通常，我们把这个关键字称为 Key，把对应的记录称为 Value，所以也可以说是通过 Key 访问一个映射表来得到 Value 的地址。而这个映射表，也叫作散列函数或者哈希函数，存放记录的数组叫作散列表。
应用场景：通讯录

8.2 哈希冲突

对于两个数据元素的关键字$k_i$和$k_j$(i$\ne$j)，有$k_i$$\ne$$k_j$，但有Hash($k_i$) = Hash($k_j$)。即：不同关键字通过相同哈希哈数计算出相同的哈希地址，该种现象称为哈希冲突或哈希碰撞。

8.3 哈希冲突解决办法

（1）开放定址法： 就是一旦发生了冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入
（2）再哈希法：同时构造多个不同的哈希函数，等发生哈希冲突时就使用第二个、第三个……等其他的哈希函数计算地址，直到不发生冲突为止。虽然不易发生聚集，但是增加了计算时间。
（3）链地址法：将所有哈希地址相同的记录都链接在同一链表中。
（4）建立公共溢出区： 将哈希表分为基本表和溢出表两部分，凡是和基本表发生冲突的元素，一律填入溢出表