高阶数据结构--位图和布隆过滤器--Java
特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函 数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种。紧凑型的、比较巧妙的概率型数据结构。七、布隆过滤器模拟实现。十、布隆过滤器应用场景。
·
目录
一、面试题
给四十亿个无符号整型,没排过序,给定一个无符号整数,如何快速判断这个数是否在这四十亿个数据中?
1.遍历 时间复杂度O(N)。
2.排序+二分查找 排序时间复杂度O(NlogN)+二分查找时间复杂度O(logN)
3. 位图解决
数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使用一个二进制比
特位来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0代表不存在。比如:
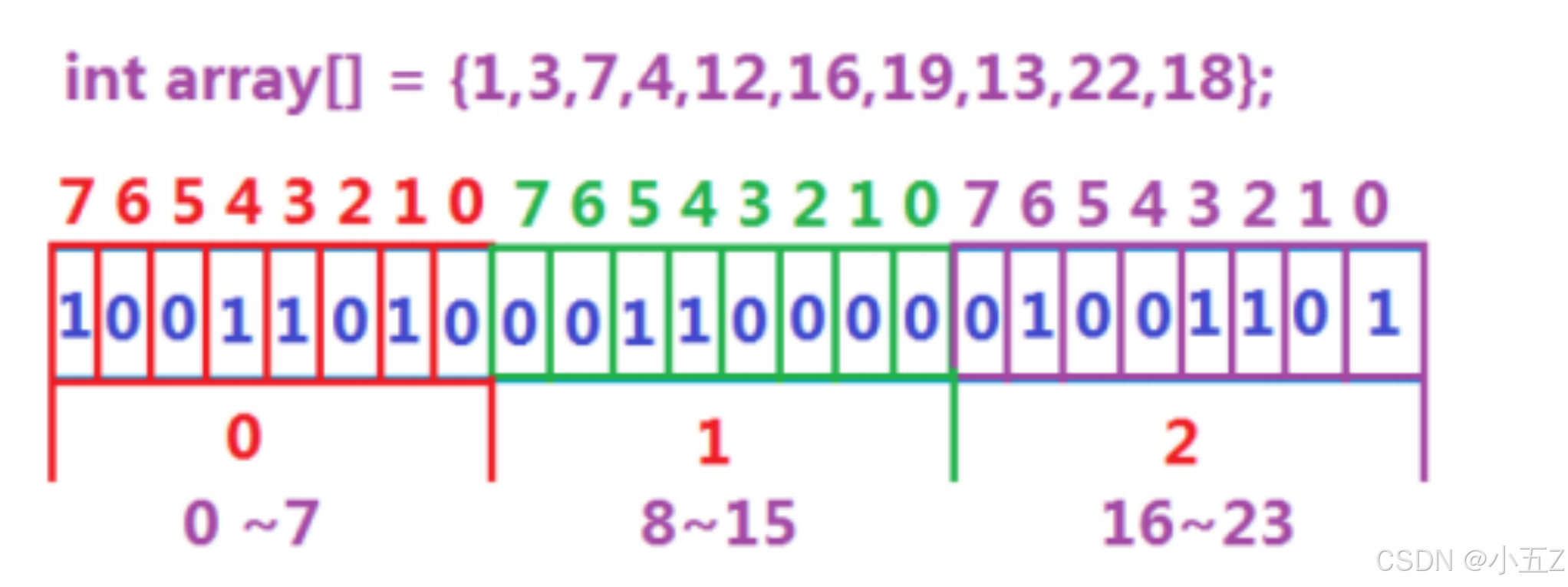
二、位图概念
所谓位图,就是用每一位来存放某种状态,适用于海量数据,整数,数据无重复的场景。通常是用来判 断某个数据存不存在的。
如上例子,10个整数本应该存放需要40个字节,此时用位图只需要3个字节。
三、模拟实现位图
import java.util.Arrays;
public class MyBitSet {
public byte[] elem;
public int CapCity;
public MyBitSet() {
elem=new byte[1];
}
public MyBitSet(int n) {
elem=new byte[n/8+1];
}
/**
* 添加元素到位图
* @param val
*/
public void set(int val) {
if(val<0) {
throw new ArrayIndexOutOfBoundsException();
}
int ArrayIndex=val/8;
int BitIndex=val%8;
if(ArrayIndex>elem.length-1) {
elem = Arrays.copyOf(elem,ArrayIndex+1);
}
elem[ArrayIndex]|=(1<<BitIndex);
CapCity++;
}
/**
* 判断位图中是否存在该元素
* @param val
* @return
*/
public boolean get(int val) {
if(val<0) {
throw new ArrayIndexOutOfBoundsException();
}
int ArrayIndex=val/8;
int BitIndex=val%8;
if(ArrayIndex>elem.length-1) {
elem = Arrays.copyOf(elem,ArrayIndex+1);
}
if((elem[ArrayIndex]&=(1<<BitIndex))!=0) {
return true;
}
return false;
}
/**
* 重置
* @param val
*/
public void reSet(int val) {
if(val<0) {
throw new ArrayIndexOutOfBoundsException();
}
int ArrayIndex=val/8;
int BitIndex=val%8;
if(ArrayIndex>elem.length-1) {
elem = Arrays.copyOf(elem,ArrayIndex+1);
}
elem[ArrayIndex]&=~(1<<BitIndex);
CapCity--;
}
public int getCapCity() {
return CapCity;
}
}可以在主函数测试一下我们简单模拟实现的位图
public class Main {
public static void main(String[] args) {
int[] array={1,3,2,5,6,7,8};
MyBitSet set=new MyBitSet();
for (int i = 0; i < array.length; i++) {
set.set(array[i]);
}
System.out.println(set.get(6));
System.out.println(set.getCapCity());
set.reSet(6);
System.out.println(set.get(6));
}
}运行结果如下:
true
7
false
进程已结束,退出代码为 0四、Java封装好的位图
我们Java自己有封装好的位图BitSet具体使用方法我们可以查阅Java文档BitSet (Java SE 21 & JDK 21)。

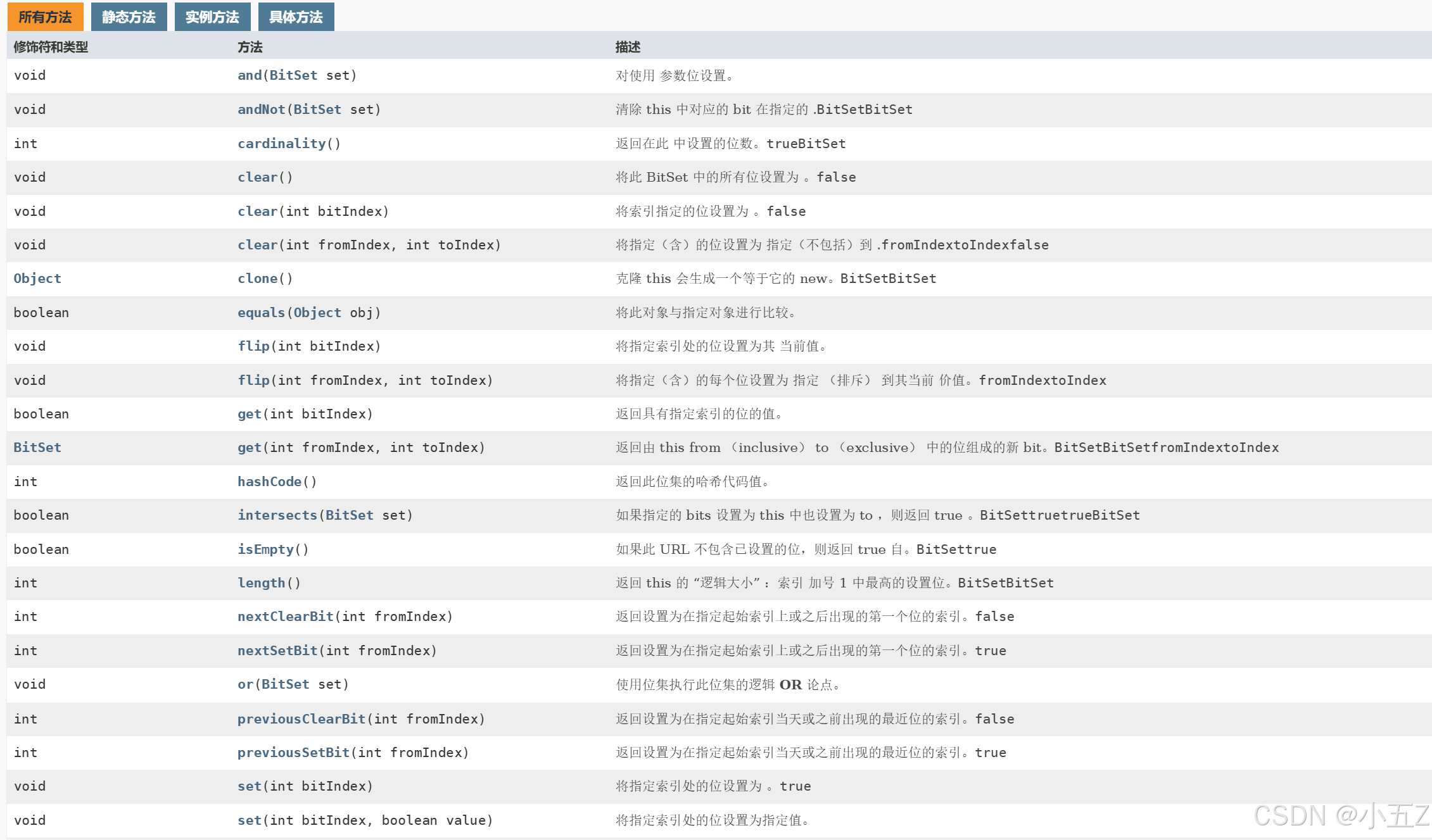
五、位图的应用
1. 快速查找某个数据是否在一个集合中
2. 排序 + 去重
3. 求两个集合的交集、并集等
4. 操作系统中磁盘块标记
六、布隆过滤器
布隆过滤器的提出
日常生活中,包括在设计计算机软件时,我们经常要判断一个元素是否在一个集合中。比如在字处理软件 中,需要检查一个英语单词是否拼写正确(也就是要判断它是否在已知的字典中);在 FBI,一个嫌疑人的 名字是否已经在嫌疑名单上;在网络爬虫里,一个网址是否被访问过等等。最直接的方法就是将集合中全部 的元素存在计算机中,遇到一个新元素时,将它和集合中的元素直接比较即可。
一般来讲,计算机中的集合是用哈希表(hash table)来存储的。它的好处是快速准确,缺点是费存储空 间。当集合比较小时,这个问题不显著,但是当集合巨大时,哈希表存储效率低的问题就显现出来了。
比如说,一个像 Yahoo,Hotmail 和 Gmai 那样的公众电子邮件(email)提供商,总是需要过滤来自发送垃 圾邮件的人(spamer)的垃圾邮件。一个办法就是记录下那些发垃圾邮件的 email 地址。由于那些发送者 不停地在注册新的地址,全世界少说也有几十亿个发垃圾邮件的地址,将他们都存起来则需要大量的网络服 务器。 如果用哈希表,每存储一亿个 email 地址, 就需要 1.6GB 的内存(用哈希表实现的具体办法是将每一个 email 地址对应成一个八字节的信息指纹,然后将这些信息指纹存入哈希表,由于哈希表的存储效率一般只有 50%,因此一个 email 地址需要占用十六个字节。一亿个地址大约要 1.6GB, 即十六亿字节的内存)。因此 存贮几十亿个邮件地址可能需要上百 GB 的内存。除非是超级计算机,一般服务器是无法存储的。
1. 用哈希表存储用户记录,缺点:浪费空间
2. 用位图存储用户记录,缺点:位图一般只能处理整形,如果内容编号是字符串,就无法处理了。
3. 将哈希与位图结合,即布隆过滤器
布隆过滤器概念
隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”,它是用多个哈希函 数,将一个数据映射到位图结构中。此种方式不仅可以提升查询效率,也可以节省大量的内存空间。
布隆过滤器的插入
比如向布隆过滤器插入“baidu”:
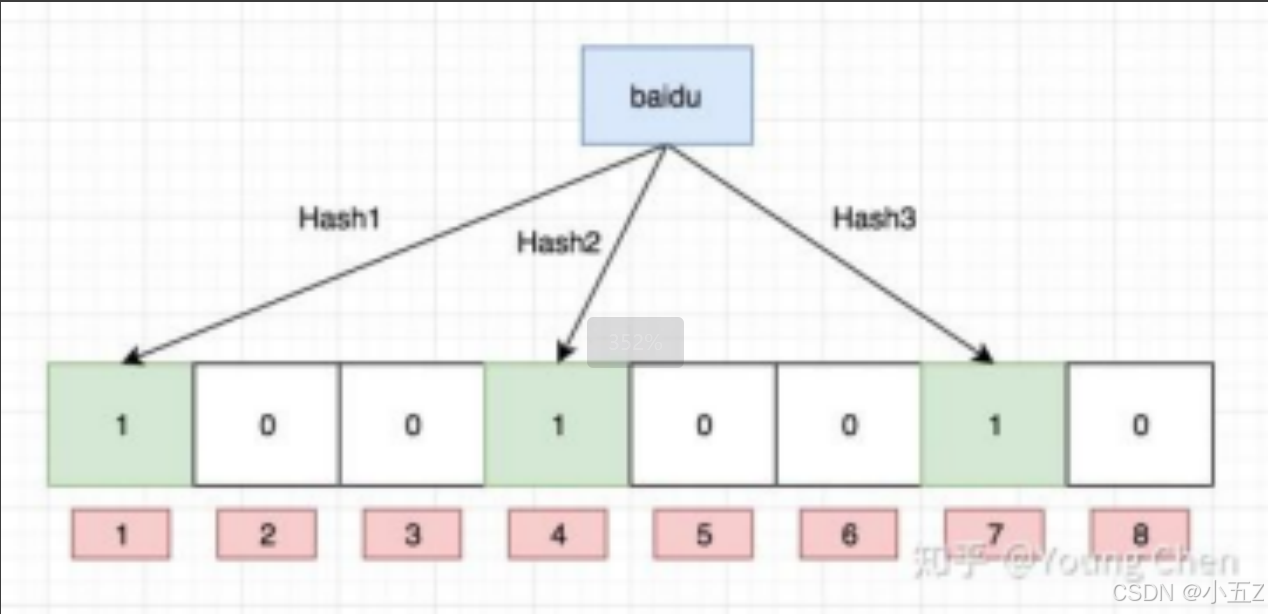
布隆过滤器的查找
布隆过滤器的思想是将一个元素用多个哈希函数映射到一个位图中,因此被映射到的位置的比特位一定为1。
所以可以按照以下方式进行查找:分别计算每个哈希值对应的比特位置存储的是否为零,只要有一个为零, 代表该元素一定不在哈希表中,否则可能在哈希表中。
注意:布隆过滤器如果说某个元素不存在时,该元素一定不存在,如果该元素存在时,该元素可能存在,因 为有些哈希函数存在一定的误判。
比如:在布隆过滤器中查找"alibaba"时,假设3个哈希函数计算的哈希值为:1、3、7,刚好和其他元素的比 特位重叠,此时布隆过滤器告诉该元素存在,但实该元素是不存在的。
七、布隆过滤器模拟实现
import java.util.BitSet;
class SimpleHash {
public int cap; //当前容量
public int seed; //随机数
public SimpleHash(int cap,int seed){
this.cap=cap;
this.seed=seed;
}
//哈希函数
public int hash(String key){
int h;
return (key == null) ? 0 :(seed*cap-1) & (h = key.hashCode()) ^ (h >>> 16);
}
}
public class MyBloomFilter {
public static final int FINAL_SIZE=1<<20;
//位图
BitSet set;
//记录了多少个数据
int UsedSize;
SimpleHash[] hash;
//随机数数组
public static final int[] seeds={9,22,3,4,55,6,77};
public MyBloomFilter() {
set=new BitSet(FINAL_SIZE);
hash=new SimpleHash[seeds.length];
for (int i = 0; i < seeds.length; i++) {
hash[i]=new SimpleHash(FINAL_SIZE,seeds[i]);
}
}
/**
* 添加元素到布隆过滤器
* @param val
*/
public void add(String val) {
for (int i = 0; i < hash.length; i++) {
int x=hash[i].hash(val);
set.set(x);
}
}
/**
* 检查元素是否存在
* @param val
* @return
*/
public boolean contains(String val){
for (int i = 0; i < hash.length; i++) {
int x=hash[i].hash(val);
if(!set.get(x)){
return false;
}
}
return true;
}
}同样的我们可以在main函数钟测试我们简单实现的布隆过滤器
class Main{
public static void main(String[] args) {
MyBloomFilter bloomFilter=new MyBloomFilter();
bloomFilter.add("hello");
System.out.println(bloomFilter.contains("hello"));
System.out.println(bloomFilter.contains("he"));
}
}运行结果如下:
true
false
进程已结束,退出代码为 0八、布隆过滤器优点
1. 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数,一般比较小),与数据量大小无关
2. 哈希函数相互之间没有关系,方便硬件并行运算
3. 布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
4. 在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
5. 数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
6. 使用同一组散列函数的布隆过滤器可以进行交、并、差运算
九、布隆过滤器缺点
1. 有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白
名单,存储可能会误判的数据)
2. 不能获取元素本身
3. 一般情况下不能从布隆过滤器中删除元素
4. 如果采用计数方式删除,可能会存在计数回绕问题
十、布隆过滤器应用场景
1. google的guava包中有对Bloom Filter的实现
2. 网页爬虫对URL的去重,避免爬去相同的URL地址。
3. 垃圾邮件过滤,从数十亿个垃圾邮件列表中判断某邮箱是否是垃圾邮箱。
4. 解决数据库缓存击穿,黑客攻击服务器时,会构建大量不存在于缓存中的key向服务器发起请求,在数 据量足够大的时候,频繁的数据库查询会导致挂机。
5. 秒杀系统,查看用户是否重复购买。

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容







所有评论(0)