C++数据结构--线性表的链式存储结构
C++数据结构--线性表的链式存储结构
1、线性表的链式存储结构
A、链式存储的定义
为了表示每个数据元素与直接后继元素之间的逻辑关系;数据元素除了存储本身的信息外,还需要存储其直接后继的信息
图示
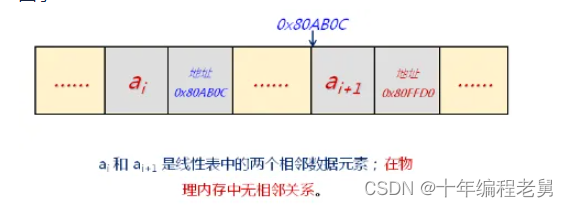
B、链式存储逻辑结构
基于链式存储结构的线性表中,每个结点都包含数据域和指针域
1.数据域:存储数据元素本身
2.指针域:存储相邻结点的地址
图示
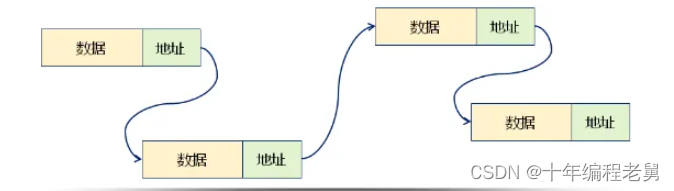
C、链表中的基本概念
1.头结点–链表中的辅助结点,包含指向第一个数据元素的指针(方便插入和删除)
2.数据结点–链表中代表数据元素的结点,表现形式为:(数据元素,地址)
3.尾节点–链表中的最后一个数据结点,包含的地址信息为空
本文福利,莬费领取Qt开发学习资料包、技术视频,内容包括(C++语言基础,Qt编程入门,QT信号与槽机制,QT界面开发-图像绘制,QT网络,QT数据库编程,QT项目实战,QSS,OpenCV,Quick模块,面试题等等)↓↓↓↓↓↓见下面↓↓文章底部点击莬费领取↓↓
代码表示为
struct Node:public Object
{
T value;
Node* next;//指向后继节点的指针
};单链表的内部结构
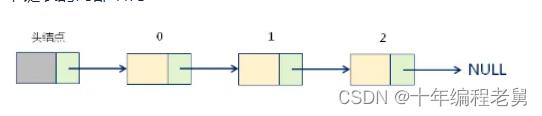
头结点在单链表中的意义是:辅助数据元素的定位,方便插入个删除操作;因此,头结点不存储实际的数据元素
D、插入与删除的实现
a.插入数据元素
1.从头结点开始,通过一个current指针定位到目标位置
2.从堆空间申请新得Node结点
3.执行操作
图示
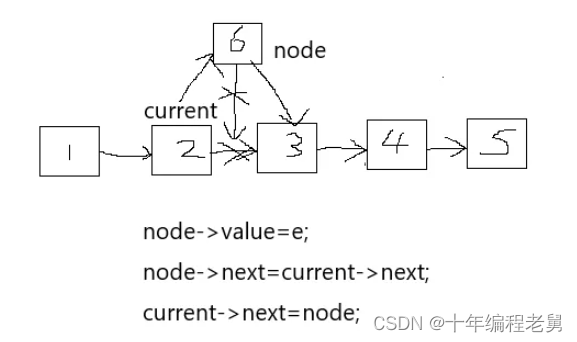
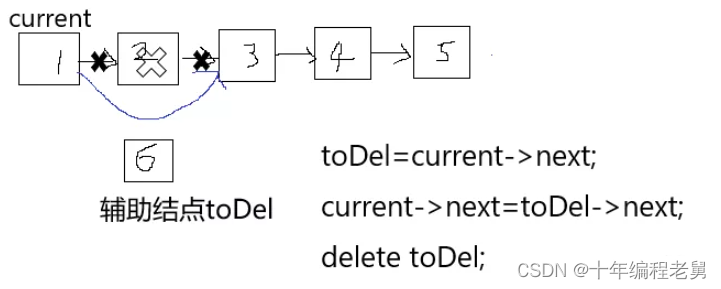
b.删除操作
1.从头结点开始,通过current指针定位到目标位置
2.使用toDel指针指向需要删除得结点
3.执行操作
图示
2、链式存储结构线性表的实现
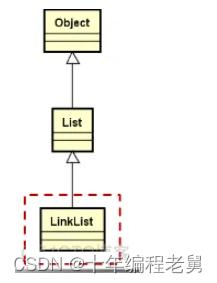
A、抽象类List的代码如下
#include "Object.h"
namespace MyLib
{
//List抽象类
template <typename T>
class List:public Object
{
protected:
List(const List&);
List& operator=(const List&);//避免赋值操作
public:
List(){}
virtual bool insert(const T&e)=0;//链表的插入
virtual bool insert(int i,const T&e)=0;//重载版本
virtual bool remove(int i)=0;//链表的删除
virtual bool set(int i,const T&e)=0;//
virtual int find(const T&e)const=0;
virtual bool get(int i,T&e)const=0;
virtual int length()const=0;
virtual void clear()=0;
};
}B、LinkList设计要点
1.类模板,通过头结点访问后继结点
2.定义内部结点类型,用于描述数据域和指针域
3.实现线性表的关键操作(增,删,查,等)
LinkList的定义,代码如下
template<typename T>
class LinkList:public List<T>
{
protected:
struct Node:public Object
{
T value;
Node* next;
};
Node m_header;
int m_length;
public:
LinkList();
.......
};LinkList的实现
template<typename T>
class LinkList:public List<T>
{
protected:
struct Node:public Object
{
T value;
Node* next;
};
mutable Node m_header;
int m_length;
public:
LinkList()
{
m_header.next=NULL;
m_length=0;
}
bool insert(const T& e)
{
return insert(m_length,e);
}
bool insert(int i,const T& e)
{
bool ret=((0<=i)&&(i<=m_length));
if(ret)
{
Node* node=new Node();
if(node!=NULL)
{
Node* current=&m_header;
for(int p=0;p<i;p++)
{
current=current->next;
}
node->value=e;
node->next=current->next;
current->next=node;
m_length++;
}
else
{
THROW_EXCEPTION(NoEoughMemoryException,"No ...");
}
}
return ret;
}
bool remove(int i)
{
bool ret=((0<=i)&&(i<=m_length));
if(ret)
{
Node* current=&m_header;
for(int p=0;p<i;p++)
{
current=current->next;
}
Node* toDel=current->next;
current->next=toDel->next;
delete toDel;
m_length--;
}
return ret;
}
bool set(int i,const T&e)
{
bool ret=((0<=i)&&(i<=m_length));
if(ret)
{
Node* current=&m_header;
for(int p=0;p<i;p++)
{
current=current->next;
}
current->next->value=e;
}
return ret;
}
int find(const T&e) const
{
int ret=-1;
int i=0;
Node* node=m_header.next;
while(node)
{
if(node->value==e)
{
ret=i;
break;
}
else
{
node=node->next;
i++;
}
}
return ret;
}
virtual T get(int i)const
{
T ret;
if(get(i,ret))
{
return ret;
}
else
{
THROW_EXCEPTION(indexOutOfBoundsException,"...");
}
return ret;
}
bool get(int i,T&e)const
{
bool ret=((0<=i)&&(i<=m_length));
if(ret)
{
Node* current=&m_header;
for(int p=0;p<i;p++)
{
current=current->next;
}
e=current->next->value;
}
return ret;
}
int length()const
{
return m_length;
}
void clear()
{
while(m_header.next)
{
Node* toDel=m_header.next;
m_header.next=toDel->next;
delete toDel;
}
m_length=0;
}
~LinkList()
{
clear();
}在编译器的实现结果如图所示
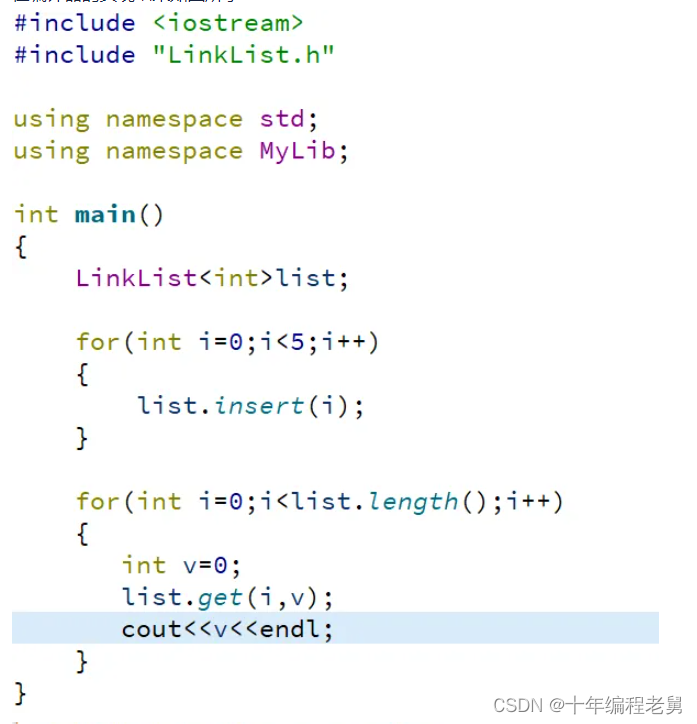
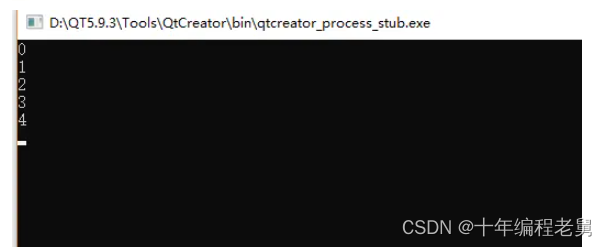
3、顺序表与单链表的对比分析
效率的深度分析:
a.插入和删除
1.顺序表:涉及大量数据对象的复制操作
2.单链表:只涉及指针操作,效率与数据对象无关
b.数据访问
1.顺序表:随机访问,可直接定位数据对象
2.单链表:顺序访问,必须从头访问数据对象,无法直接定位
工程开发中的选择:
顺序表:
1.数据元素的类型相对简单,不涉及拷贝
2.数据元素相对稳定,访问操作远多于插入和删除操作
单链表:
1.数据元素的类型相对复杂,复制操作相对耗时
2.数据元素不稳定,需要经常插入和删除,访问操作较少
总结:
1.线性表中元素的查找依赖于相等比较操作符
2.顺序表适用于访问需求量较大的场合(随机访问)
3.单链表适用于数据元素频繁插入删除的场合(顺序访问)
4.当数据类型相对简单时,顺序表和单链表的效率不相上下
4、单链表的遍历与优化
a、代码的优化
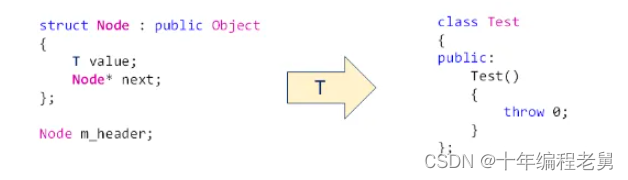
在单链表的实现中有代码的重复
mutable struct:public Object//没有类型名的结构
{
char reserved[sizeof(T)];
Node* next;
} m_header;//头节点 辅助定位元素
Node* position(int i) const//程序优化
{
Node* ret=reinterpret_cast<Node*(&m_header);//reinterpret_cast强制类型转换
for(int p=0;p<i;p++)
{
ret=ret->next;
}
return ret;
}
Node* create()
{
return new Node();
}
void destroy(Node* pn)
{
delete pn;
}插入部分的修改如图所示

b、单链表的遍历设计思路
当前实现的单链表类不能以线性的时间复杂度完成单链表的遍历,所以需要重新设计一种思路
1.在单链表的内部定义一个游标(Node* m_current)
2.遍历开始前将游标指向位置为0的数据元素
3.获取游标指向的数据元素
4.通过结点中的next指针移动游标

c、遍历函数原型设计
bool move(int i,int step=1);//step每次结点的移动
bool end();
T current();
bool next();
代码实现如下
/*遍历函数的实现*/
virtual bool move(int i,int step=1)
{
bool ret= (0<=i)&&(i<m_length)&&(step>0);
if(ret)
{
m_current=position(i)->next;
m_step=step;
}
return ret;
}
virtual bool end()
{
return (m_current==NULL);
}
virtual T current()
{
if(!end())
{
return m_current->value;
}
else
{
THROW_EXCEPTION(InvalidOperationException,"...");
}
}
virtual bool next()
{
int i=0;
while((i<m_step)&& (!end()))
{
m_current=m_current->next;
i++;
}
return (i==m_step);
}最终的实现如下图所示
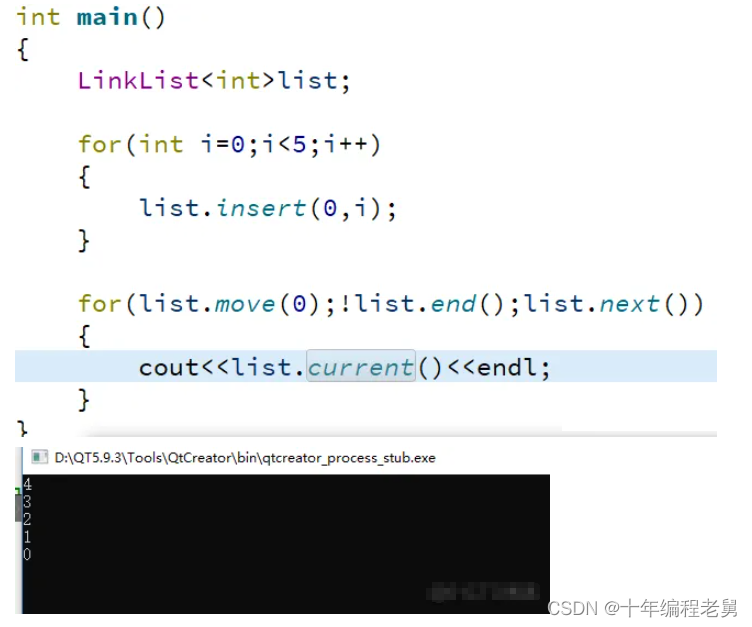
小结:
1.单链表的遍历需要在线性时间内完成
2.在单链表内部定义游标变量,通过游标遍历提高效率
3.遍历相关的成员函数是相互依赖,相互配合的关系
4.封装结点的申请和删除操作更有利于增强扩展性
本文福利,莬费领取Qt开发学习资料包、技术视频,内容包括(C++语言基础,Qt编程入门,QT信号与槽机制,QT界面开发-图像绘制,QT网络,QT数据库编程,QT项目实战,QSS,OpenCV,Quick模块,面试题等等)↓↓↓↓↓↓见下面↓↓文章底部点击莬费领取↓↓

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献7条内容
已为社区贡献7条内容







所有评论(0)