数据结构--哈夫曼树
以上都是哈夫曼树在含有n个带权叶结点的二叉树中,其中带权路径长度WPL最小的二叉树\color{red}带权路径长度(WPL)最小的二叉树带权路径长度WPL最小的二叉树称为哈夫曼树\color{red}哈夫曼树哈夫曼树,也称最优二叉树\color{red}最优二叉树最优二叉树。
数据结构–哈夫曼树
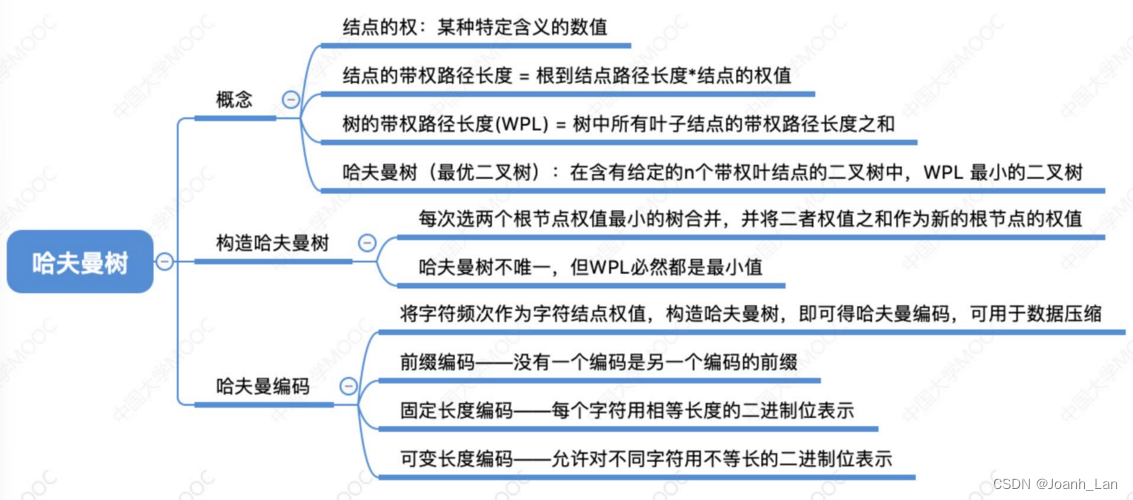
带权路径长度
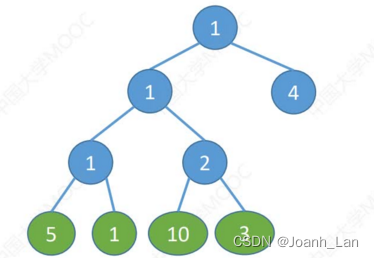
结点的权\color{red}权权:有某种现实含义的数值(如:表示结点的重要性等)
结点的带权路径长度\color{red}结点的带权路径长度结点的带权路径长度:从树的根到该结点的路径长度(经过的边数)与该结点上权值的乘积树的带权路径长度\color{red}树的带权路径长度树的带权路径长度:树中所有叶结点\color{red}叶结点叶结点的带权路径长度之和(WPL, Weighted Path Length)
WPL=∑i=1nwili\mathrm{WPL}=\sum_{i=1}^{n}w_{i}l_{i}WPL=∑i=1nwili
哈夫曼树的定义
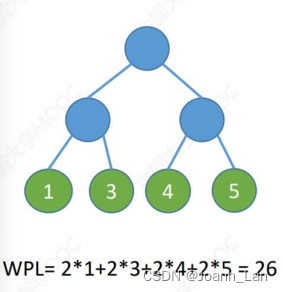
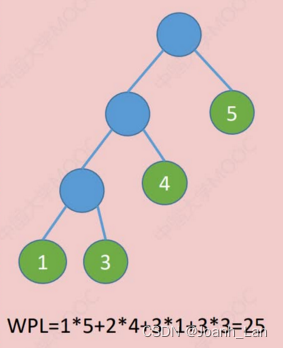
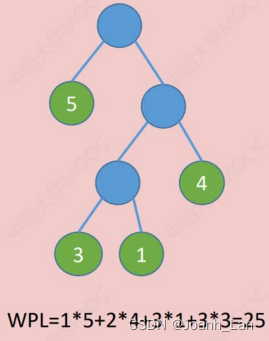
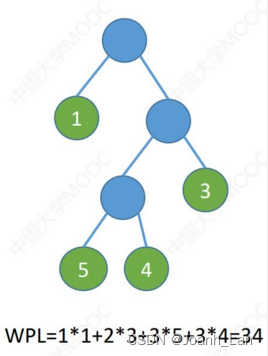
以上都是哈夫曼树
在含有n个带权叶结点的二叉树中,其中带权路径长度(WPL)最小的二叉树\color{red}带权路径长度(WPL)最小的二叉树带权路径长度(WPL)最小的二叉树称为哈夫曼树\color{red}哈夫曼树哈夫曼树,也称最优二叉树\color{red}最优二叉树最优二叉树
哈夫曼树的构造
给定n个权值分别为w1,w2...,wnw_1, w_2..., w_nw1,w2...,wn的结点,构造哈夫曼树的算法描述如下:
1)将这n个结点分别作为n棵仅含一个结点的二叉树,构成森林F。
2)构造一个新结点,从F中选取两棵根结点权值最小的树作为新结点的左、右子树,并且将新结点的权值置为左、右子树上根结点的权值之和。
3)从F中删除刚才选出的两棵树,同时将新得到的树加入F中。
4)重复步骤2)和3),直至F中只剩下一棵树为止。
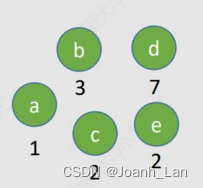
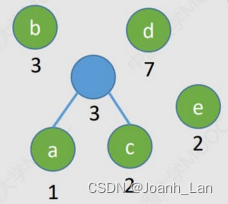
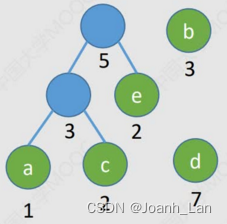
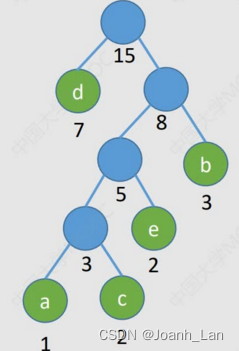
1)每个初始结点最终都成为叶结点,且权值越小的结点到根结点的路径长度越大
2)哈夫曼树的结点总数为2n -1
3)哈夫曼树中不存在度为1的结点。
4)哈夫曼树并不唯一,但wPL必然相同且为最优
WPLmin=1∗7+2∗3+3∗2+4∗1+4∗2=31WPL_{min}=1^*7+2^*3+3^*2+4^*1+4^*2=31WPLmin=1∗7+2∗3+3∗2+4∗1+4∗2=31
哈夫曼编码
电报――点、划两个信号(二进制0/1)
固定长度编码――每个字符用相等长度的二进制位表示
可变长度编码\color{red}可变长度编码可变长度编码――允许对不同字符用不等长的二进制位表示
若没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码\color{red}前缀编码前缀编码
有哈夫曼树得到哈夫曼编码\color{red}哈夫曼编码哈夫曼编码――字符集中的每个字符作为一个叶子结点,各个字符出现的频度作为结点的权值,根据之前介绍的方法构造哈夫曼树
若哈夫曼树不唯一,则对应的哈夫曼编码不唯一\color{green}若哈夫曼树不唯一,则对应的哈夫曼编码不唯一若哈夫曼树不唯一,则对应的哈夫曼编码不唯一
哈夫曼编码可用于数据压缩\color{pink}哈夫曼编码可用于数据压缩哈夫曼编码可用于数据压缩
知识点回顾与重要考点

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献12条内容
已为社区贡献12条内容







所有评论(0)