快速理解二叉树的遍历
本文的代码实现涉及到C++的STL的Vector和Queue

二叉树的遍历

`

从物理结构的角度来看，树是一种基于链表的数据结构，因此其遍历方式是通过指针逐个访问节点。然而，树是一种非线性数据结构，这使得遍历树比遍历链表更加复杂，需要借助探索算法来实现。

一、二叉树的层序遍历

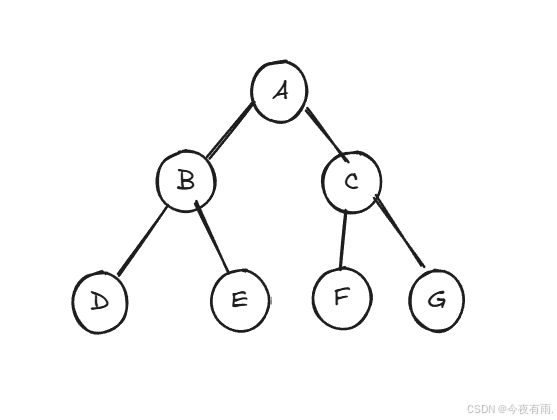
我们以上图作为例题：
所谓层序遍历（level-order traversal）就是从树的顶部到底部逐层遍历二叉树，并在每一层按照从左到右的顺序访问节点。层序遍历本质上属于广度优先遍历（breadth-first traversal）(以后的文章会讲到)，其也称广度优先遍历（breadth-first search，BFS）。它体现了一种‘’一圈一圈向外拓展‘的逐层遍历方式。
如图所示：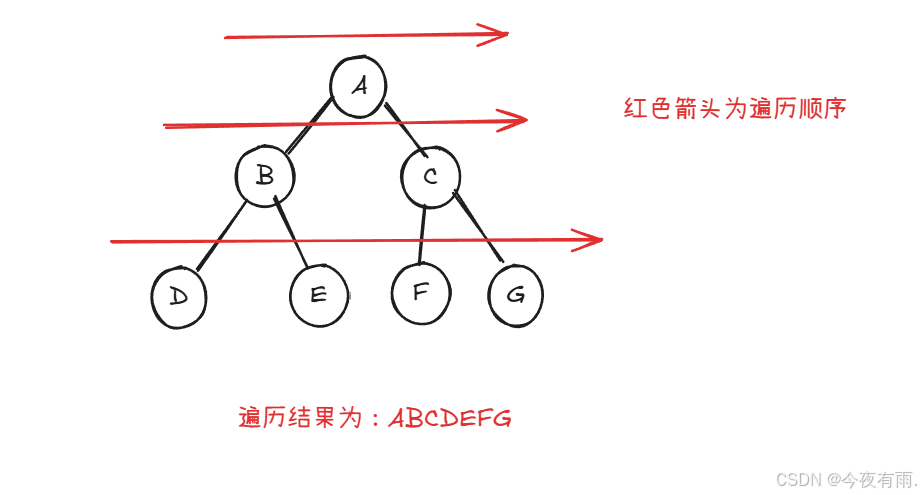

接下来我们用代码来实现树的层序遍历

#include <iostream>
#include<vector>
#include<queue>
using namespace std;
//二叉树节点的结构体
typedef struct TreeNode
{
	char value;//节点值
	TreeNode* left;//左孩子指针
	TreeNode* right;//右孩子指针
	//节点的构造函数,初始化节点的左右孩子为空
	TreeNode(char x) :value(x), left(nullptr), right(nullptr) {}
};


//代码实现层序遍历
vector<char> levelOrder(TreeNode* root)
{
	//初始化队列
	queue<TreeNode*> queue;
	queue.push(root);
	//初始化一个列表，用于保存遍历序列
	vector<char> vec;
	while (!queue.empty())
	{
		TreeNode* node = queue.front();
		queue.pop();       //队列出队
		vec.push_back(node->value);  //保存队列的节点值
		if(node->left != nullptr)
		{
			queue.push(node->left);    //左子节点入队
		}
		if (node->right != nullptr)
		{
			queue.push(node->right);   //右子节点入队
		}
	}
	return vec;
}

int main()
{
	//初始化一个二叉树
	TreeNode *A = new TreeNode('A');
	TreeNode* B = new TreeNode('B');
	TreeNode* C = new TreeNode('C');
	TreeNode* D = new TreeNode('D');
	TreeNode* E = new TreeNode('E');
	TreeNode* F = new TreeNode('F');
	TreeNode* G = new TreeNode('G');
	A->left = B;
	A->right = C;
	B->left = D;
	B->right = E;
	C->left = F;
	C->right = G;

	// 获取层序遍历结果
	vector<char> result = levelOrder(A);

	// 输出结果
	for (auto value : result) {
		cout << value << " "; // 输出层序遍历节点的值
	}
	cout << endl;

	// 释放内存
	delete A;
	delete B;
	delete C;
	delete D;
	delete E;
	delete F;
	delete G;
	
	return 0;
}
时间复杂度为O（n），所有的节点都被访问一次，使用O（n）时间，其中n为节点数量
空间复杂度为O（n），在最差情况下，即为满二叉树，遍历到最底层之前，队列中最多同时存在(n+1)/2个节点，占用O（n）空间

输出的结果就是：

二、二叉树的前序、中序、后序遍历

二叉树的前序、中序、后序遍历都属于深度优先遍历(depth-first traversal)，也称为升读优先搜索(depth-first search,DFS),它体现了一种“先走到尽头，再回溯继续”的遍历方式。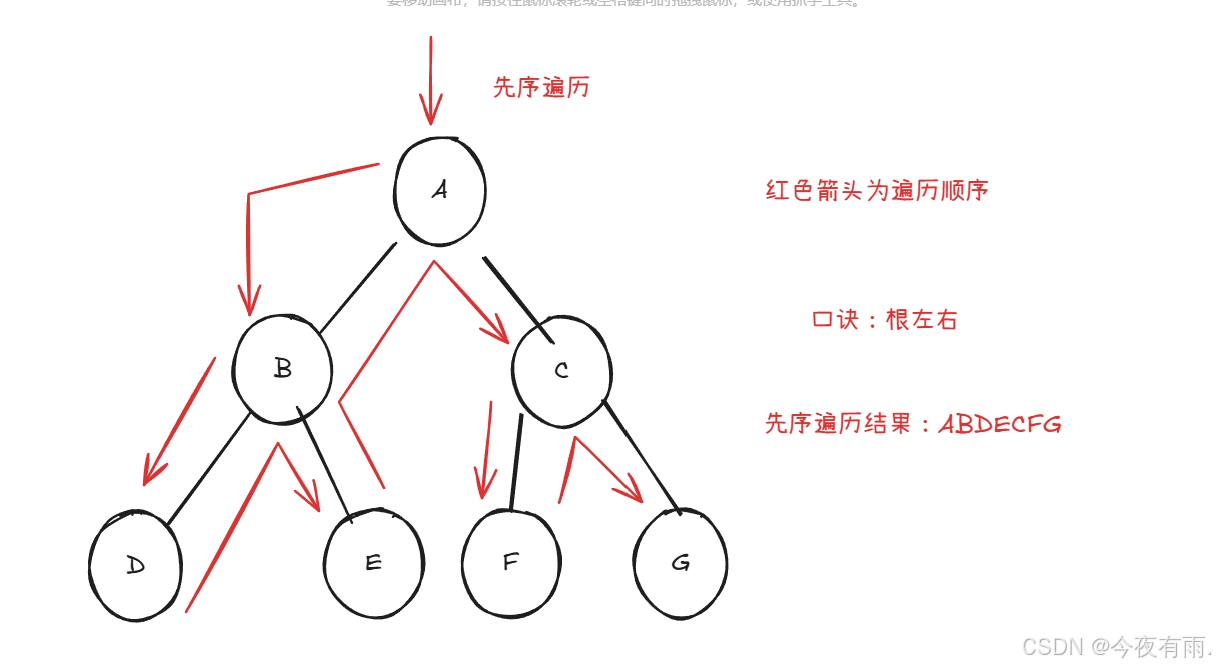



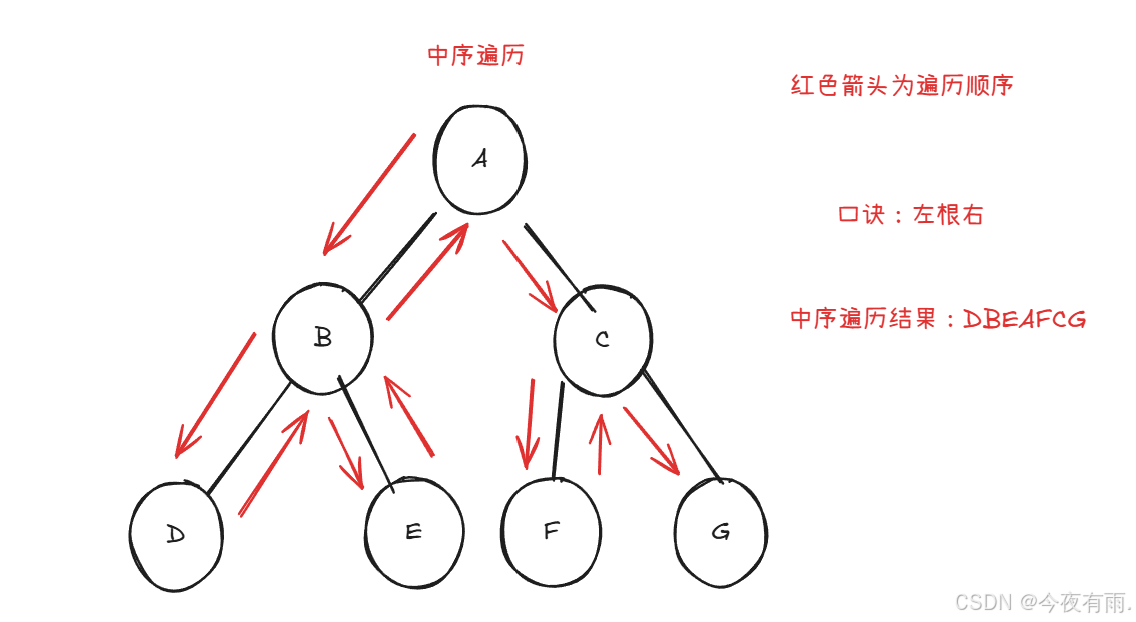
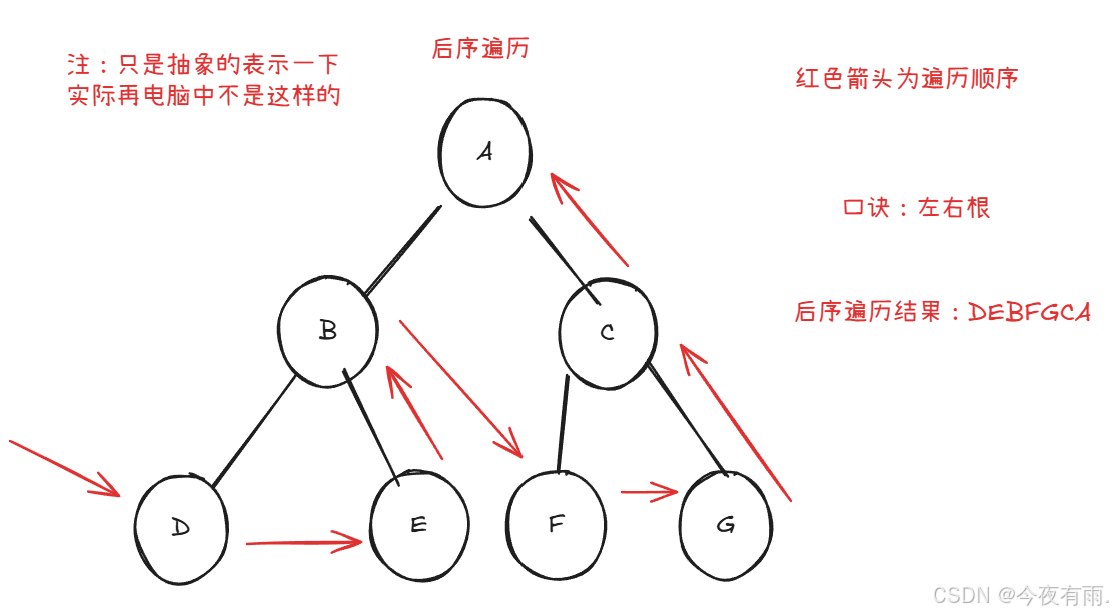
上图展示了对二叉树进行深度优先遍历的工作原理。深度优先遍历就像是绕着整棵二叉树的外围走了一圈，在每个节点都会遇到三个位置，分别对应前序遍历、中序遍历和后序遍历。
接下来我们将用递归的方法来实现前序、中序、后序遍历

#include <iostream>
#include<vector>
#include<queue>
using namespace std;
//二叉树节点的结构体
typedef struct TreeNode
{
	char value;//节点值
	TreeNode* left;//左孩子指针
	TreeNode* right;//右孩子指针
	//节点的构造函数,初始化节点的左右孩子为空
	TreeNode(char x) :value(x), left(nullptr), right(nullptr) {}
};

//前序遍历
void preOrder(TreeNode* root)
{
	//初始化一个列表，用于保存遍历序列
	vector<char> vec;
	if (root == nullptr)
	{
		return;
	}
	cout << root->value << " "; // 输出当前节点值

	//访问优先级：根节点-》左子树-》右子树
	vec.push_back(root->value);
	preOrder(root->left);
	preOrder(root->right);
}
//中序遍历
void midOrder(TreeNode* root)
{
	//初始化一个列表，用于保存遍历序列
	vector<char> vec;
	if (root == nullptr)
	{
		return;
	
	}
	//访问优先级：左子树-》根节点-》右子树
	midOrder(root->left);
	cout << root->value << " "; // 输出当前节点值
	vec.push_back(root->value);
	midOrder(root->right);
}

//后续遍历
void endOrder(TreeNode* root)
{
	//初始化一个列表，用于保存遍历序列
	vector<char> vec;
	if (root == nullptr)
	{
		return;
	}
	//访问优先级左子树-》右子树-》根节点
	endOrder(root->left);
	endOrder(root->right);
	vec.push_back(root->value);

	cout << root->value << " "; // 输出当前节点值
}

int main()
{
	//初始化一个二叉树
	TreeNode *A = new TreeNode('A');
	TreeNode* B = new TreeNode('B');
	TreeNode* C = new TreeNode('C');
	TreeNode* D = new TreeNode('D');
	TreeNode* E = new TreeNode('E');
	TreeNode* F = new TreeNode('F');
	TreeNode* G = new TreeNode('G');
	A->left = B;
	A->right = C;
	B->left = D;
	B->right = E;
	C->left = F;
	C->right = G;

	std::cout << "前序遍历: ";
	preOrder(A);
	cout << endl;

	cout << "中序遍历: ";
	midOrder(A);
	std::cout << endl;

	cout << "后序遍历: ";
	endOrder(A);
	cout << endl;
	
	// 释放内存
	delete A;
	delete B;
	delete C;
	delete D;
	delete E;
	delete F;
	delete G;
	
	return 0;
}
时间复杂度为O（n）,所有节点都被访问一次，使用O（n）的时间
空间复杂度为O（n），在最差情况下，即树退化成链表时，递归深度达到n，系统占用O（n）栈帧空间

上图为代码的运行结果图。

总结

希望本文章可以帮助到刚学习到二叉树的同学。
路漫漫，学习之路还很长远。