文章目录

前引

因为这几篇lab内容都不是很多
而且确实也是因为我是想早点把lab1给结束掉 学习后面的新课程了

再加上这一个后面还有3个 lab 所以就一个一个简单的来讲一讲吧

2025/07/17 13:40 早上走到公司的路上 被人撞了一下 耳机掉在路上 被汽车碾了:（
花了400块钱重新去闲鱼配了一个 早上也浪费了一上午的时间 各种看怎么维修 天才吧 重新配对等等 中午去公司健身房澡也没洗
好吧 我还是赶紧把这些内容给补了 今天才能看新内容呢

从零开始的机器学习之路（十一）---- Optional Lab 12-17 分类&逻辑回归&决策边界&损失函数&逻辑回归梯度下降&开销函数

1、Optional Lab 12 分类

1、Classification Start

这一章其实就是简单了解一下 分类是什么
下面举了一些例子 比如是否是垃圾邮件 电信诈骗等等

对于这些场景 其实分类就是0 和 1这样的分类情况 这个其实是和线性回归是比较有差别的 也就是 0 1场景

在这里插入图片描述

2、可视化分类

下面的图其实也就是把数据可视化了出来

一个是单变量 一个是双变量

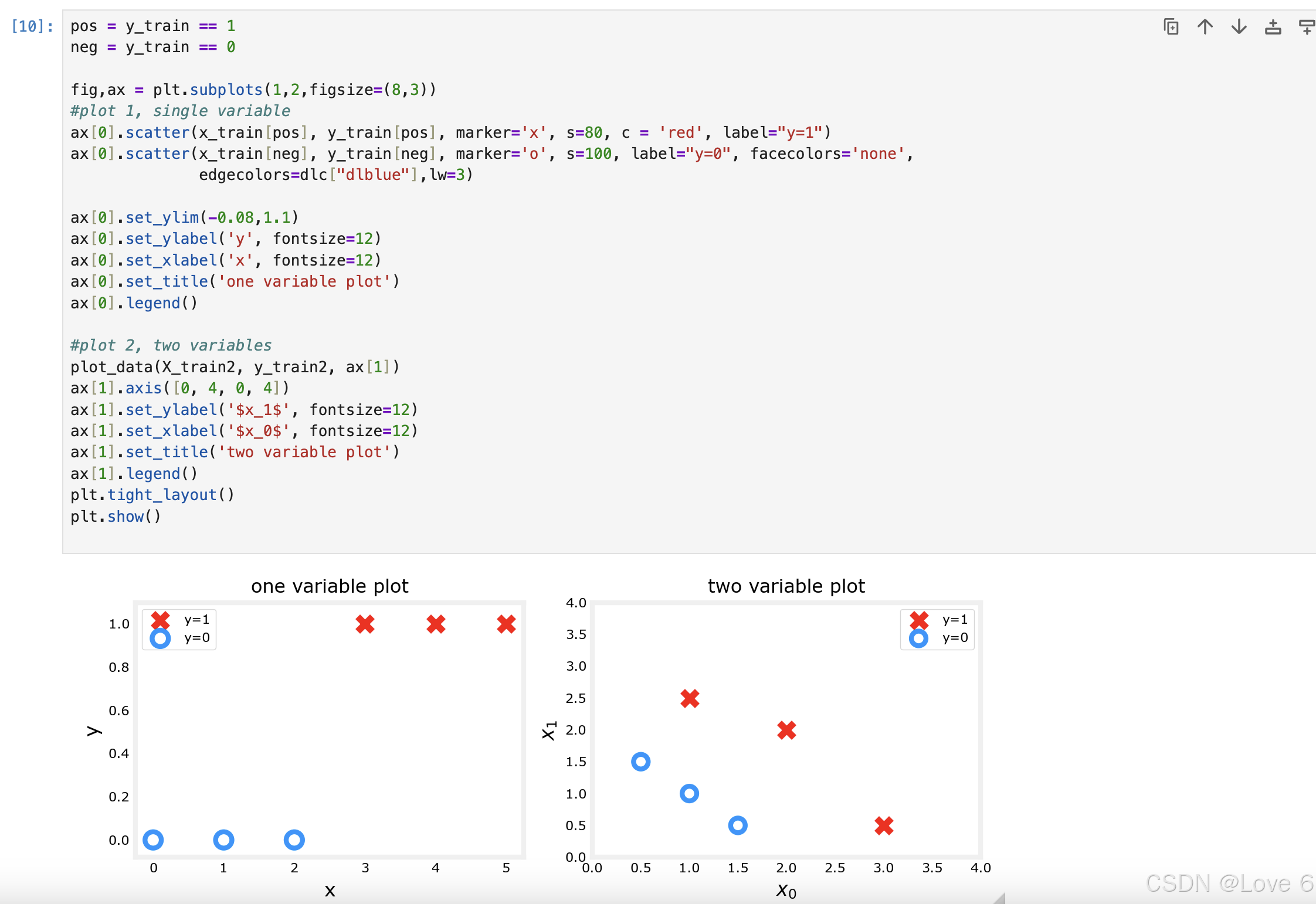
在这里插入图片描述

下面则是用线性回归来预测当前的模型 其实可以发现 拟合的效果并不好
而且如果用0.5来预测的话 发现其实预测的也并不好 所以从这里也能得到 线性回归 并不适用于分类

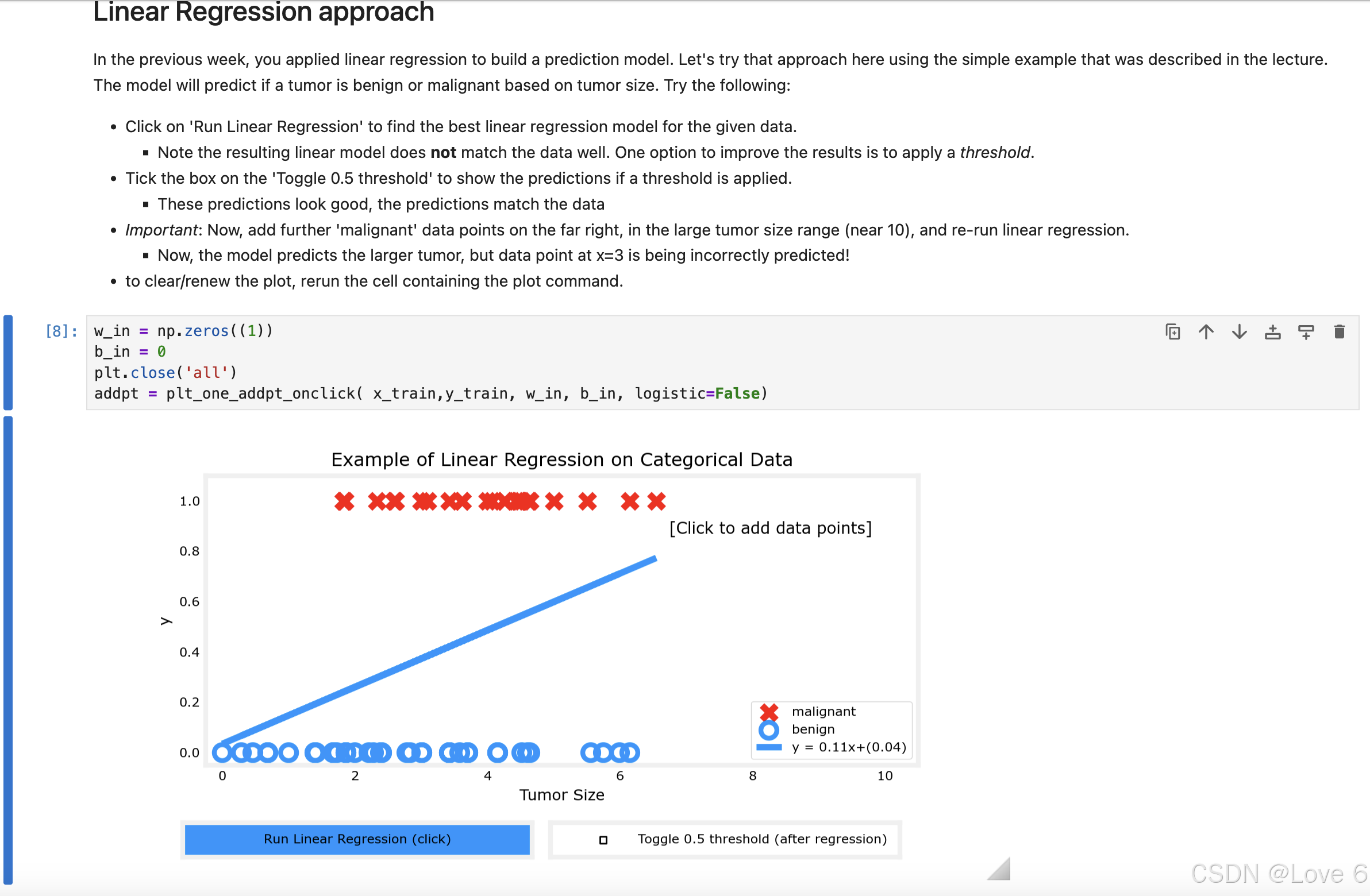
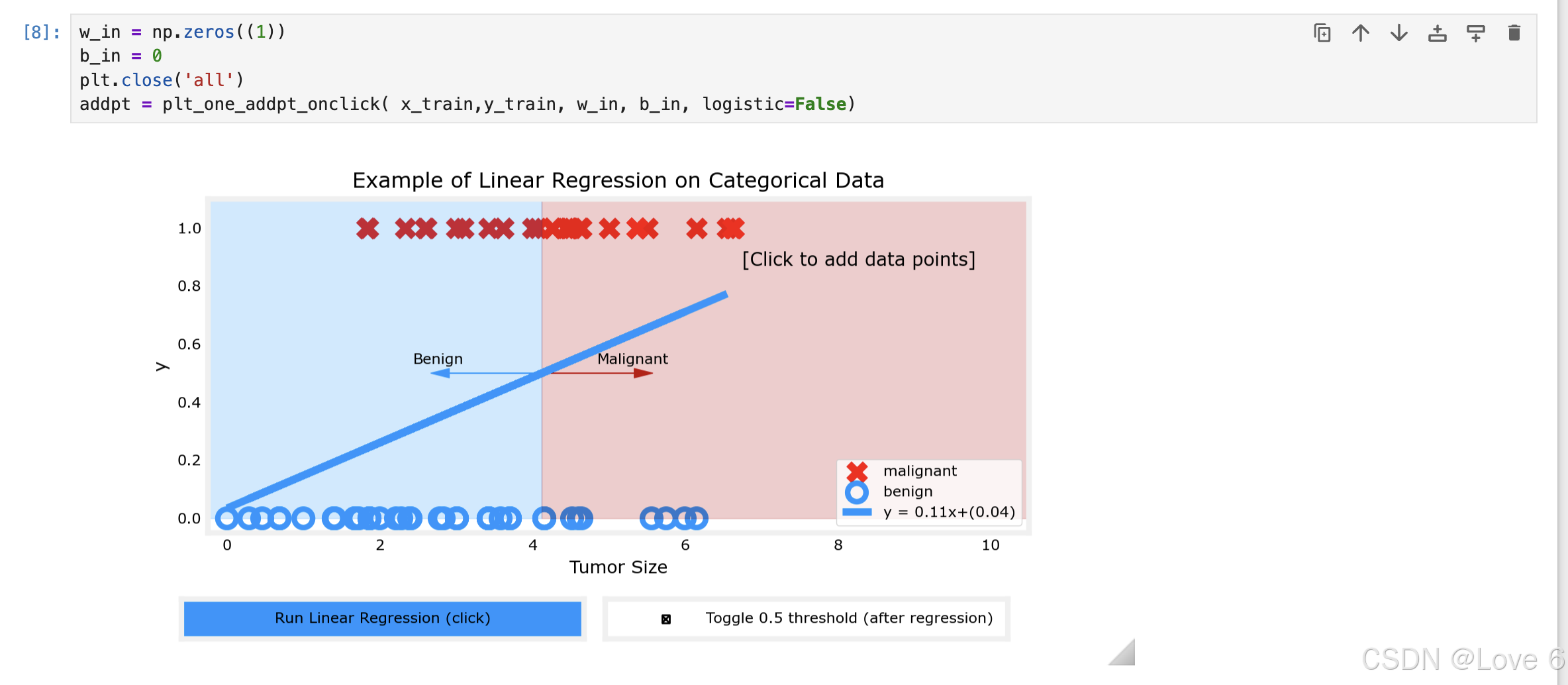
在这里插入图片描述

在这里插入图片描述

2、Optional Lab 13 逻辑回归

1、Sigmoid Or Logistic Function Start

Sigmoid 函数其实我们很早的就学过了

也就是1 / 1 + e^-z 这样的函数 我们可以认为这样的函数形式 其实针对于我们的分类或者说是逻辑回归模型 是更合适的

这一章最主要就是简单介绍了一下 大概也写了一下回归函数实现

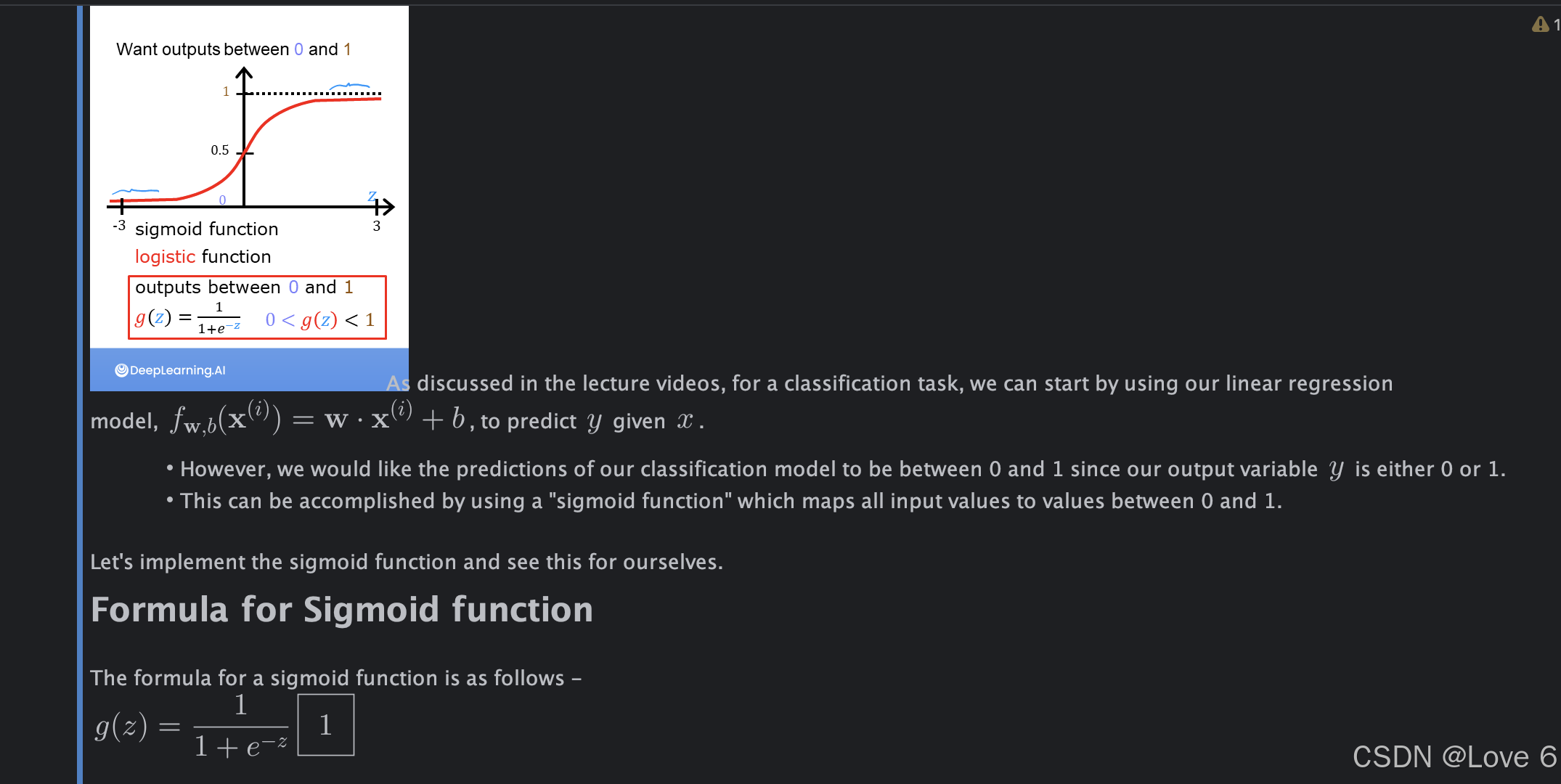
在这里插入图片描述

2、Sigmoid

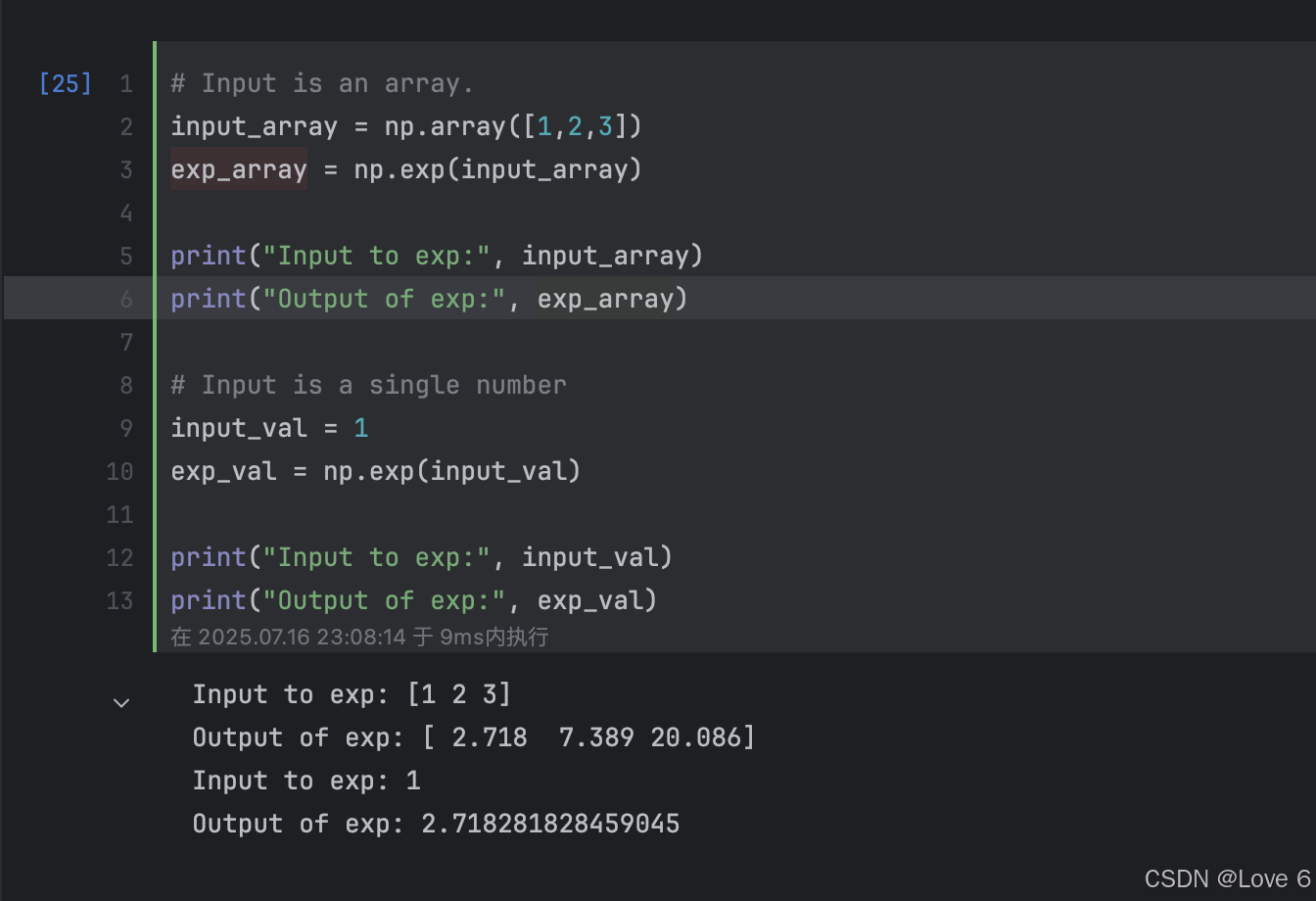
下面即简单介绍了一下 numpy包如何用到e的 exp即可以对当前向量相乘
e作为标量 其实也就是一个2.718这样的一个数 高中数学也学过

实现这样的一个函数 在python中即是这样实现

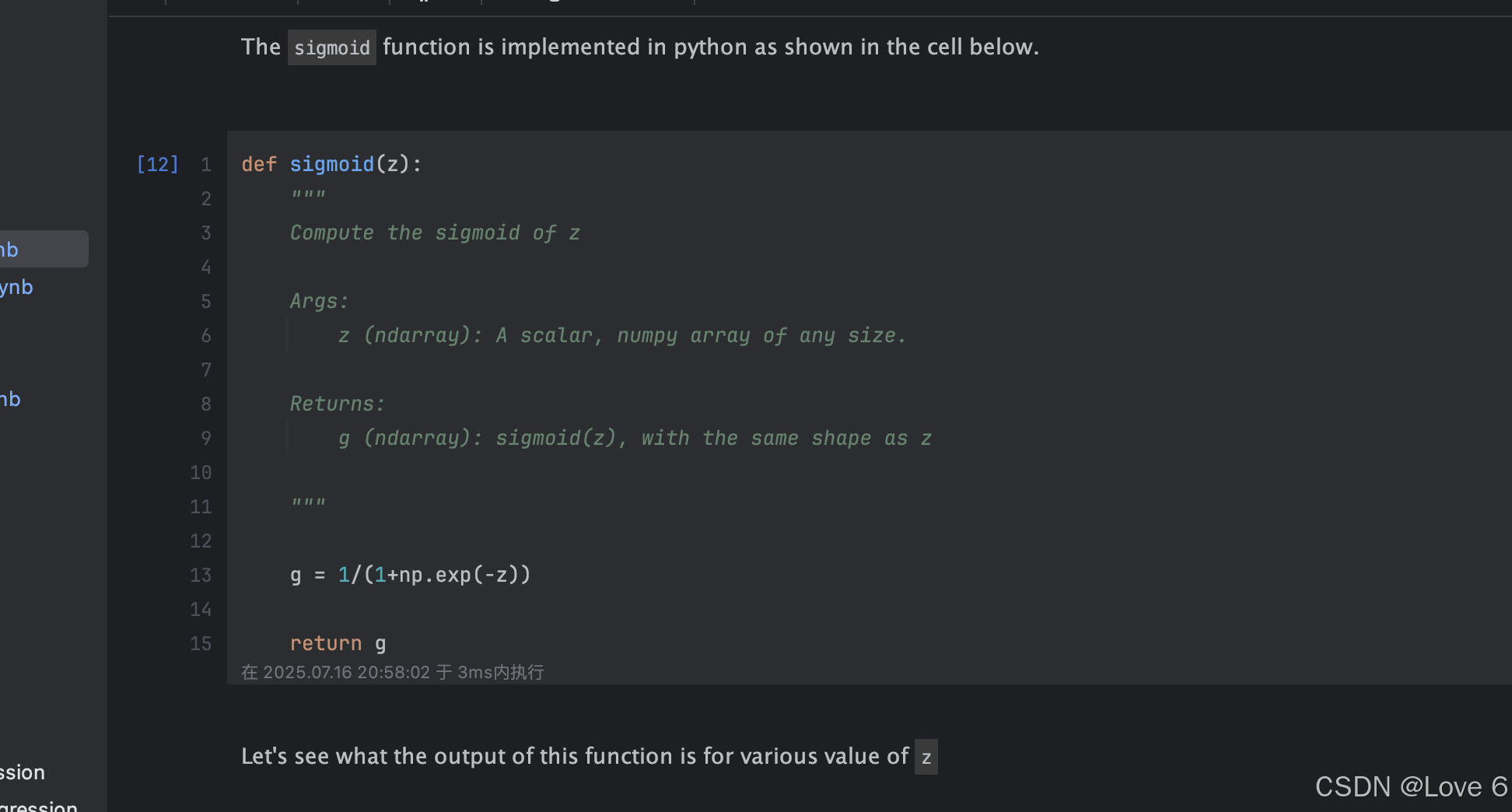
在这里插入图片描述
在这里插入图片描述

def sigmoid(z):
    """
    Compute the sigmoid of z

    Args:
        z (ndarray): A scalar, numpy array of any size.

    Returns:
        g (ndarray): sigmoid(z), with the same shape as z
         
    """

    g = 1/(1+np.exp(-z))
   
    return g
3、可视化模拟

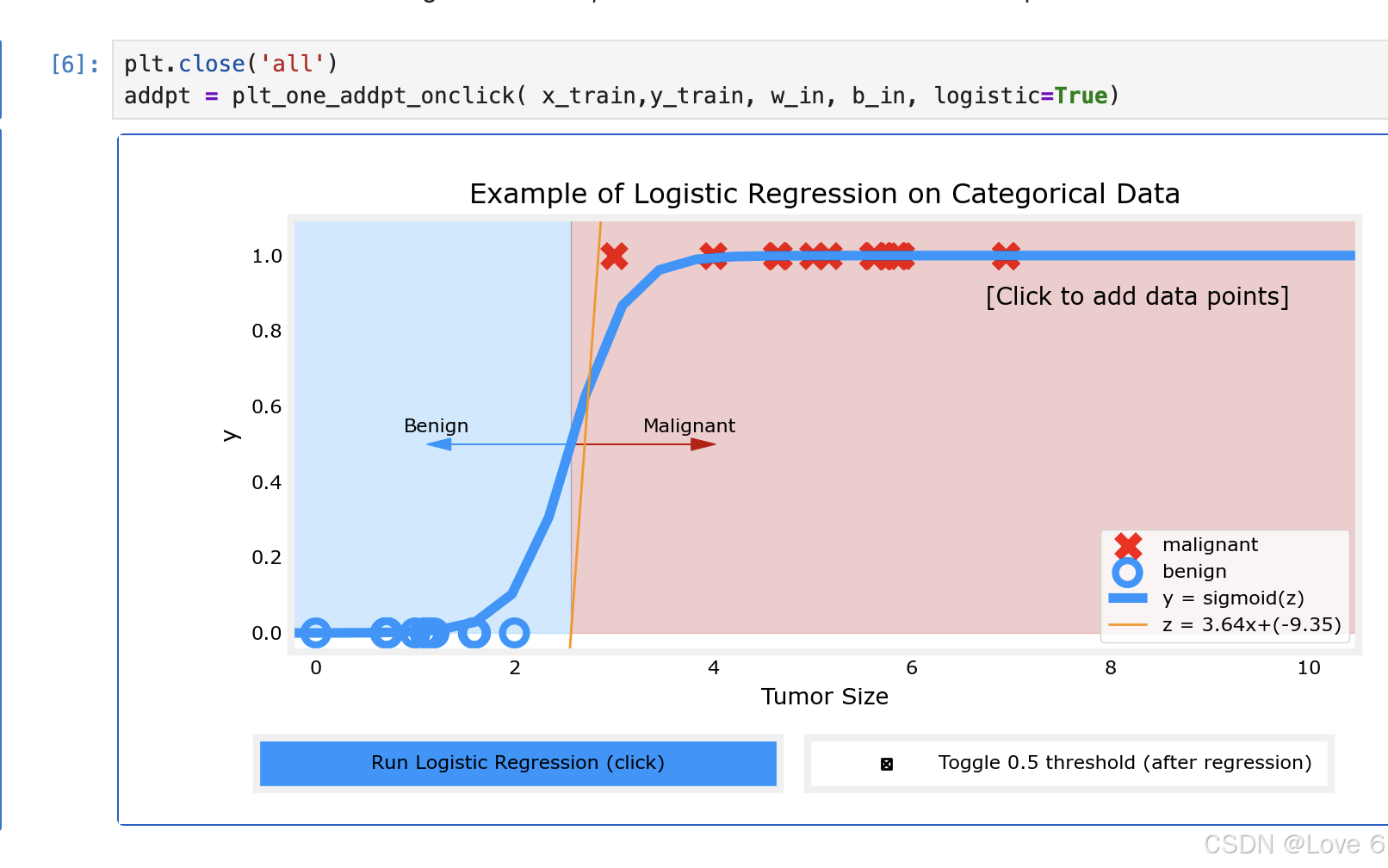
这里用这个逻辑回归模型来预测 发现确实准了很多
相比而言确实是更适合当前分类场景的

在这里插入图片描述

3、Optional Lab 14 决策边界

1、Decision Boundary Start

其实这一个lab很简单 就是简单的让我们认识什么是决策边界
其实参考下面的Sig 当结果大于0.5时 我们可以认为 分类就是1 小于0.5时 我们认为分类就是0 且横轴也可以看出来也就是 大于0 和 小于0 即是分类1 和 0

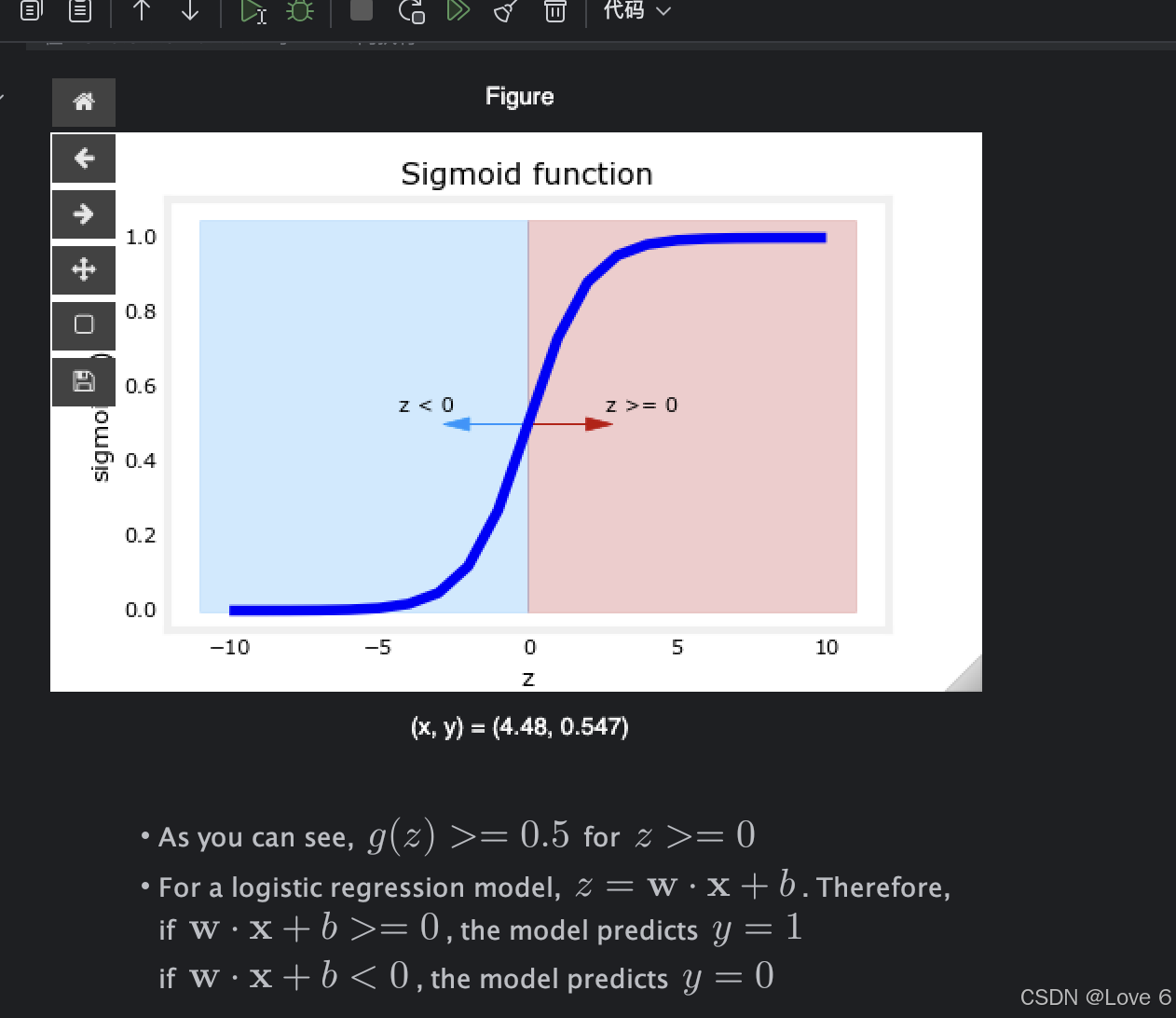
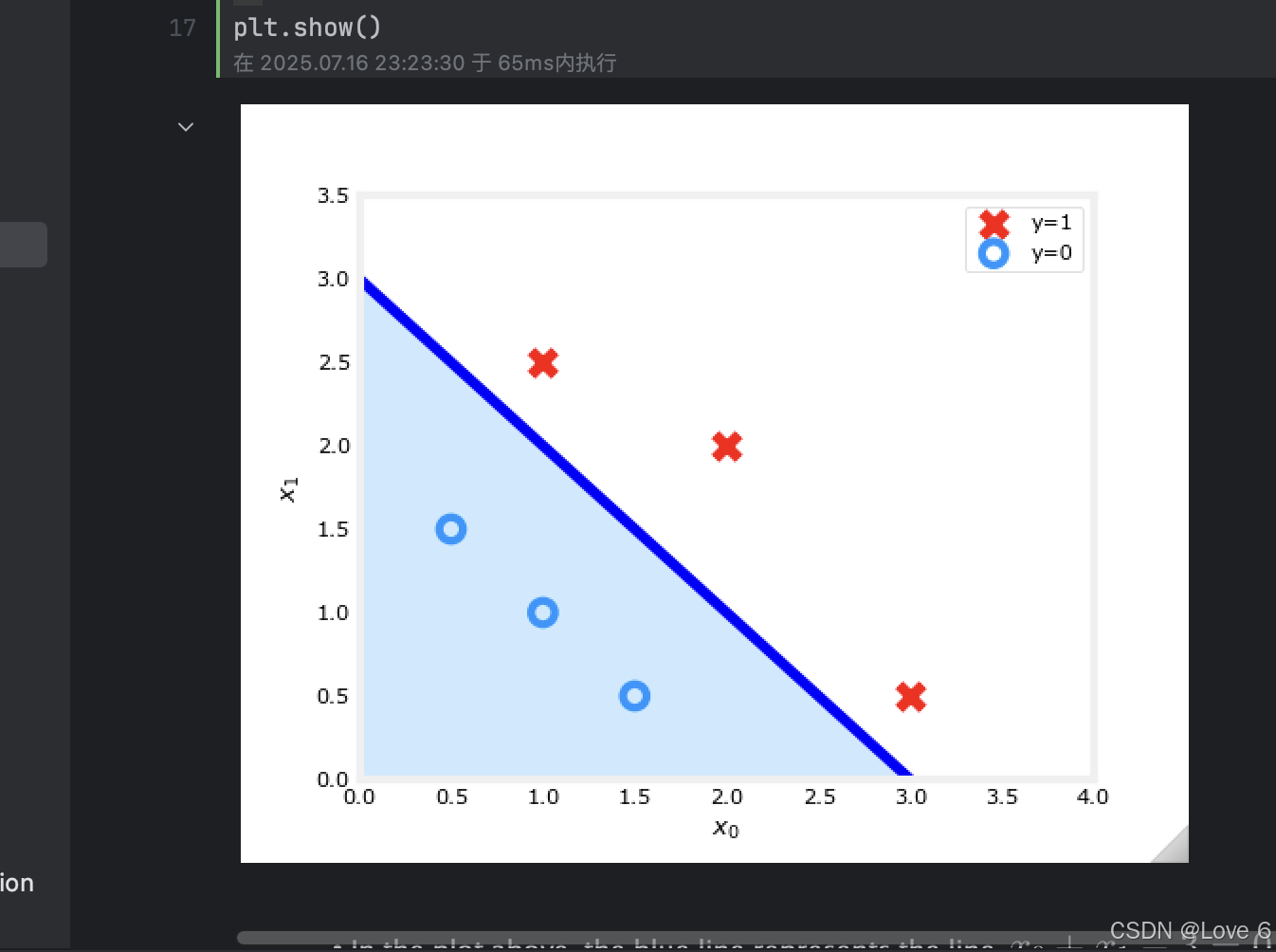
在这里插入图片描述

2、可视化决策边界

从这里能看出来 当在y轴下面的时候 即是x < 0的时候
然后也就是sig函数是偏左的 y = 0
在y轴上方的时候 即是x > 0的时候 也就是y = 1

在这里插入图片描述

4、Optional Lab 15 损失函数

1、Logistic Loss Start

其实这一章 比较简单 就是了一下 逻辑回归 开销函数不应该选用 均方误差 然后给了一个新的公式
目前逻辑回归的应该选用的损失函数

而且损失函数 其实应该比较好的 应该是选择一个凸函数来用

2、可视化 均方误差 Vs 现Logistic Loss Function

从这里能看到 其实目前的均方误差并不是一个凸函数的方式 而且这样去找全局最低点 能看出如果去迭代其实应该效果会非常不好

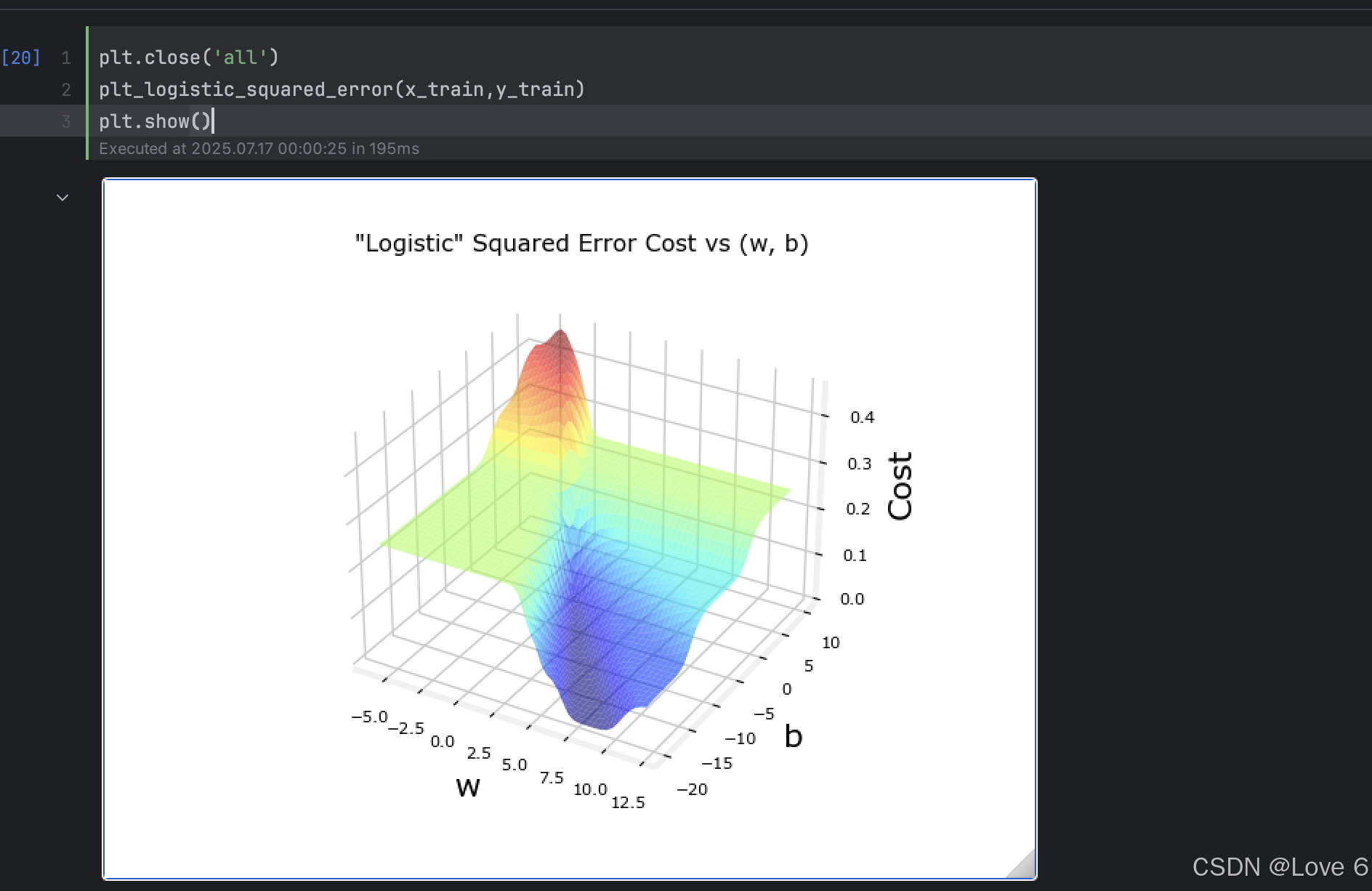
在这里插入图片描述

而针对下面公式的推导 针对逻辑回归的loss function 则是下面的公式 其实我觉得这里参考视频可以理解的更清楚一些
第一个if y == 1 此时对于当预期值靠近0时 此时可以认为效果是很不好的 参考下方第二张图的左边部分
而对于第二个if y == 0时 此时认为 预期值靠近1时 也认为开销时很大的 查考右边部分 而对于整个开销函数 可以用下面的一个公式来代替

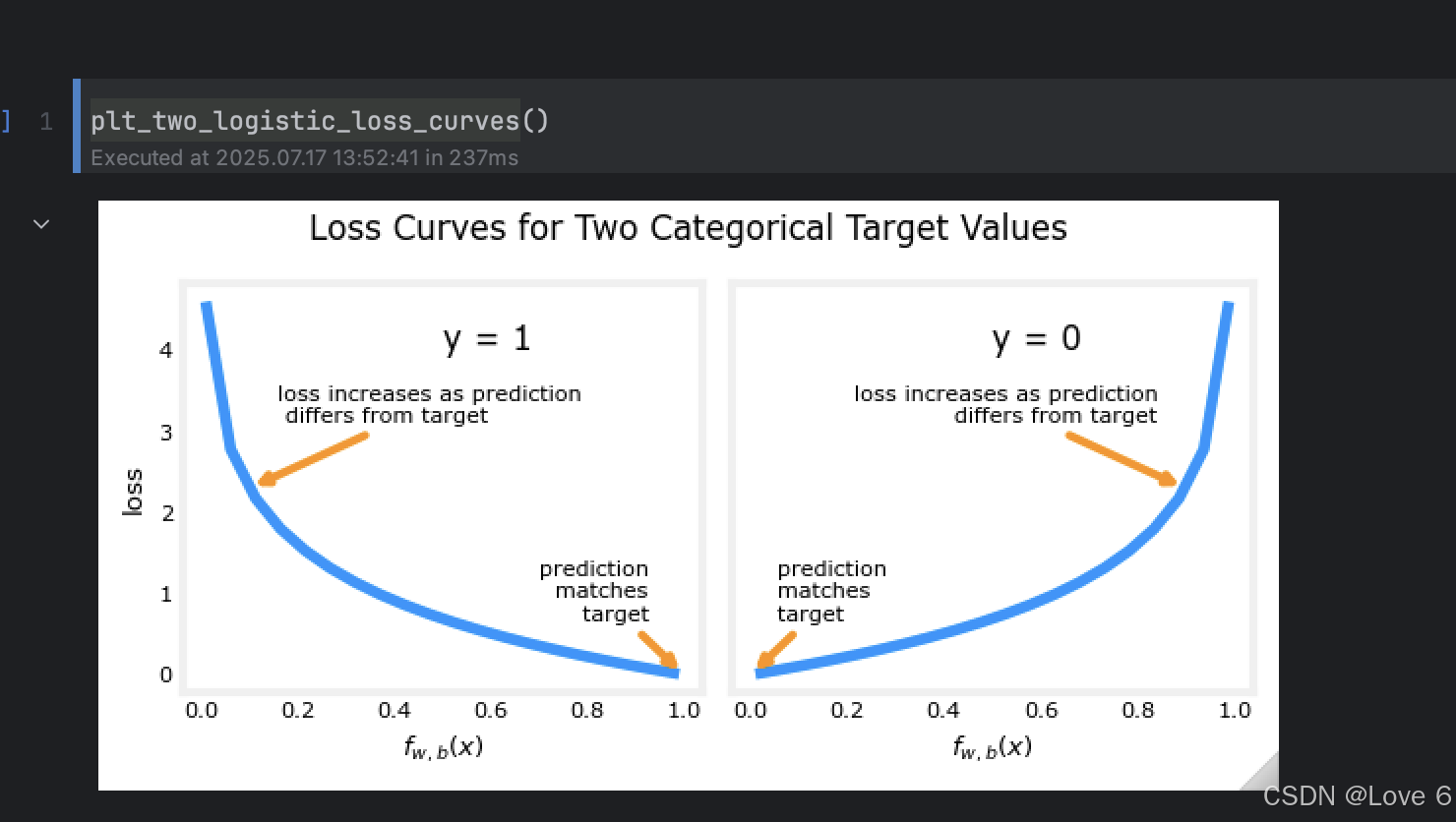
在这里插入图片描述
在这里插入图片描述

如下所得

在这里插入图片描述

5、Optional Lab 16 开销函数

1、Cost Function for Logistic Regression Start

这里其实就是简单的进行数学公式推导 介绍一些 开销函数
这里也就简单带过讲讲吧

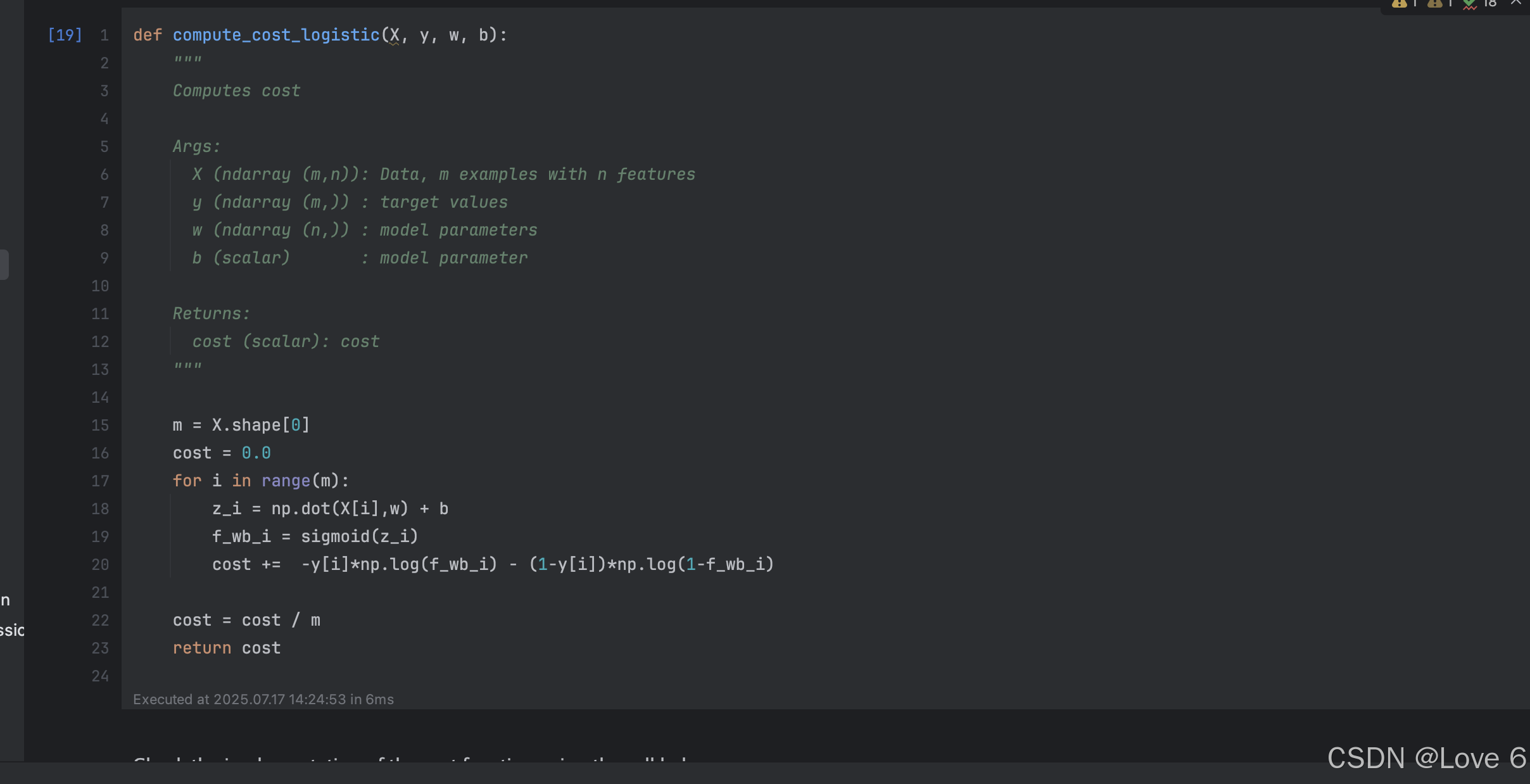
2、Compute Cost function

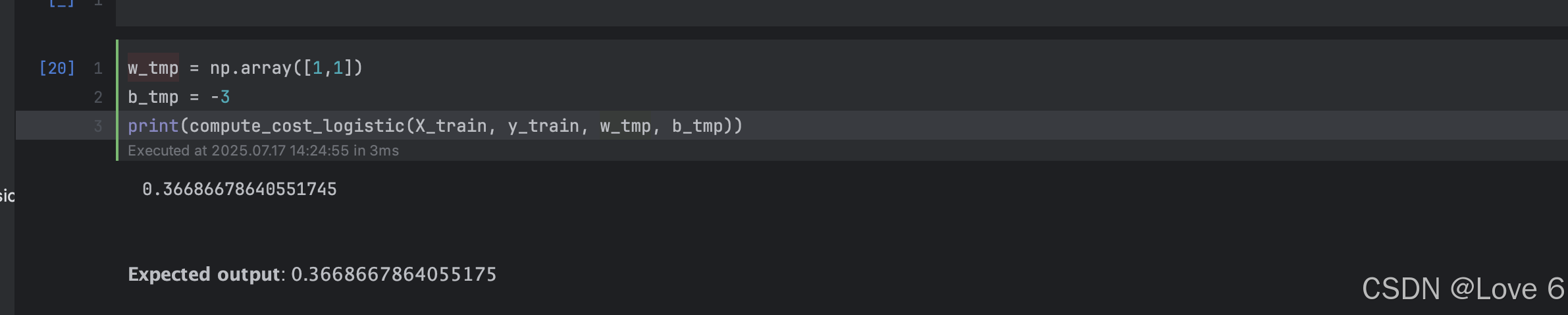
这里其实也就是带入到开销函数去
带入公式 然后简单计算一下 这一章就结束了

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

6、Optional Lab 17 梯度下降

1、Gradient Descent for Logistic Regression Start

这里其实也就是 梯度函数推导 以及 可视化结果 让我们能直观感受

这里就是全部的推导内容了 ：）

在这里插入图片描述

2、Compute Gradient Logistic

这里的代码实现也就是下面了 其实也就是参考上面公式去写的

def compute_gradient_logistic(X, y, w, b): 
    """
    Computes the gradient for linear regression 
 
    Args:
      X (ndarray (m,n): Data, m examples with n features
      y (ndarray (m,)): target values
      w (ndarray (n,)): model parameters  
      b (scalar)      : model parameter
    Returns
      dj_dw (ndarray (n,)): The gradient of the cost w.r.t. the parameters w. 
      dj_db (scalar)      : The gradient of the cost w.r.t. the parameter b. 
    """
    m,n = X.shape
    dj_dw = np.zeros((n,))                           #(n,)
    dj_db = 0.

    for i in range(m):
        f_wb_i = sigmoid(np.dot(X[i],w) + b)          #(n,)(n,)=scalar
        err_i  = f_wb_i  - y[i]                       #scalar
        for j in range(n):
            dj_dw[j] = dj_dw[j] + err_i * X[i,j]      #scalar
        dj_db = dj_db + err_i
    dj_dw = dj_dw/m                                   #(n,)
    dj_db = dj_db/m                                   #scalar
        
    return dj_db, dj_dw

这里实现的结果也就如下所呈现的一样的 迭代了数据

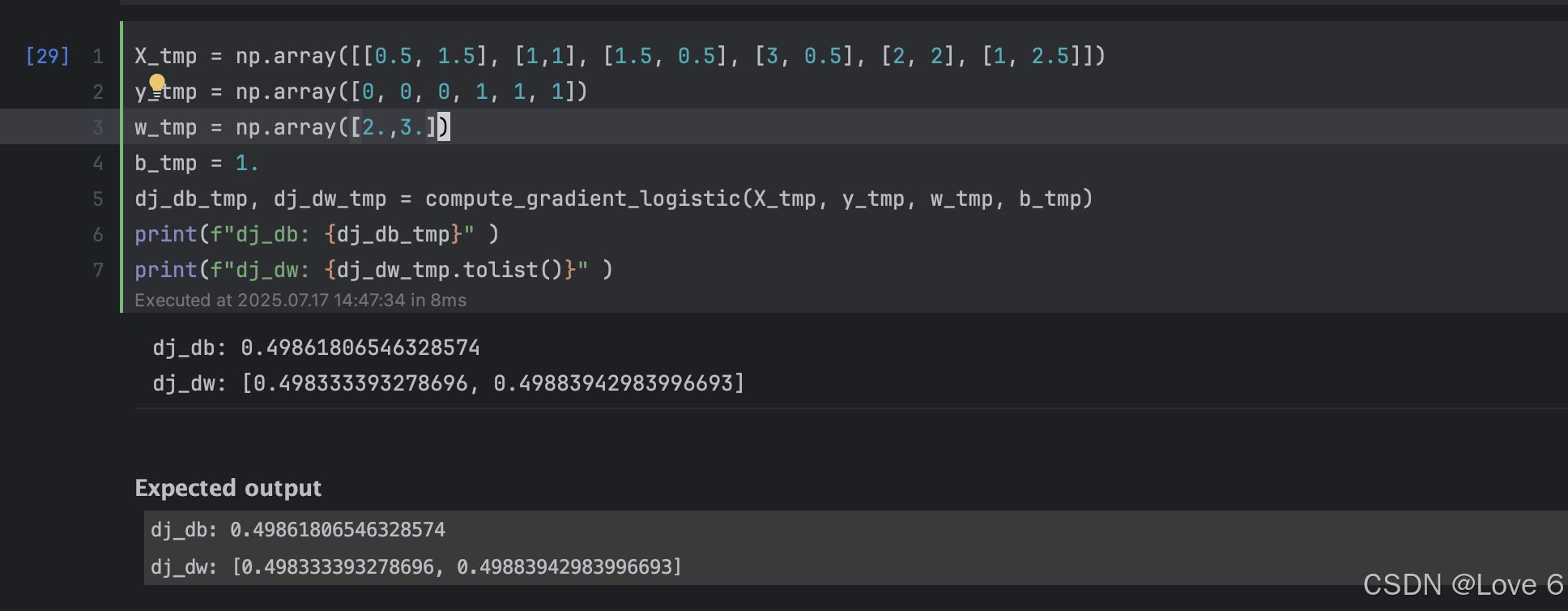
在这里插入图片描述

3、Gradient Descent

这里的梯度下降函数 其实和之前的线性回归 基本上是一摸一样的 毕竟刻子和思路都是一样的 ：）
下方即是代码

def gradient_descent(X, y, w_in, b_in, alpha, num_iters): 
    """
    Performs batch gradient descent
    
    Args:
      X (ndarray (m,n)   : Data, m examples with n features
      y (ndarray (m,))   : target values
      w_in (ndarray (n,)): Initial values of model parameters  
      b_in (scalar)      : Initial values of model parameter
      alpha (float)      : Learning rate
      num_iters (scalar) : number of iterations to run gradient descent
      
    Returns:
      w (ndarray (n,))   : Updated values of parameters
      b (scalar)         : Updated value of parameter 
    """
    # An array to store cost J and w's at each iteration primarily for graphing later
    J_history = []
    w = copy.deepcopy(w_in)  #avoid modifying global w within function
    b = b_in
    
    for i in range(num_iters):
        # Calculate the gradient and update the parameters
        dj_db, dj_dw = compute_gradient_logistic(X, y, w, b)   

        # Update Parameters using w, b, alpha and gradient
        w = w - alpha * dj_dw               
        b = b - alpha * dj_db               
      
        # Save cost J at each iteration
        if i<100000:      # prevent resource exhaustion 
            J_history.append( compute_cost_logistic(X, y, w, b) )

        # Print cost every at intervals 10 times or as many iterations if < 10
        if i% math.ceil(num_iters / 10) == 0:
            print(f"Iteration {i:4d}: Cost {J_history[-1]}   ")
        
    return w, b, J_history         #return final w,b and J history for graphing

有了我们的实际代码 我们可以实际训练看一下预期效果
发现迭代出来 数据

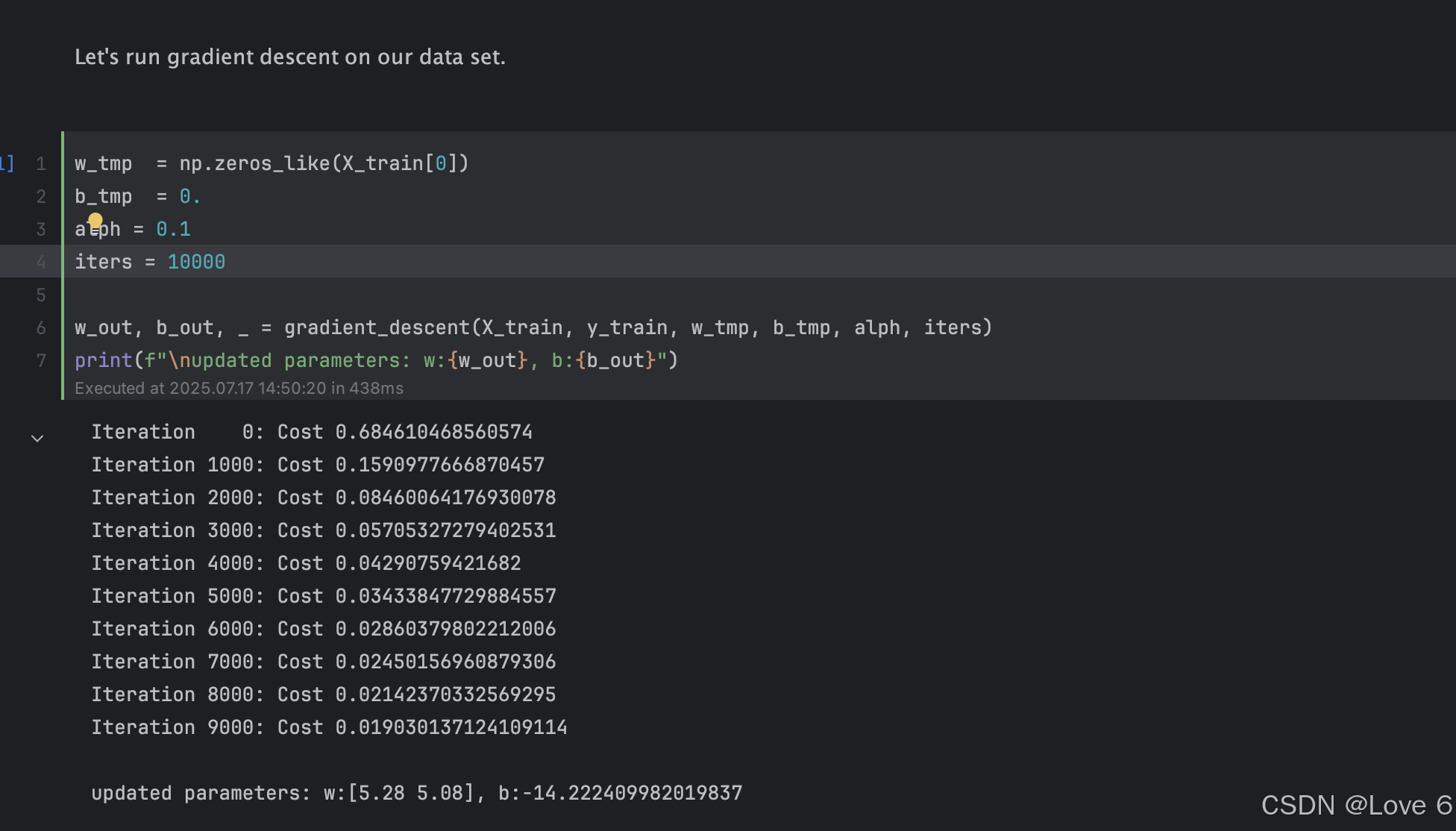
在这里插入图片描述

我们把实际迭代的数据 放到下面的图标中展示 我们可以认为蓝色线上方的就是y == 1的区域 y == 0则是 0的区域

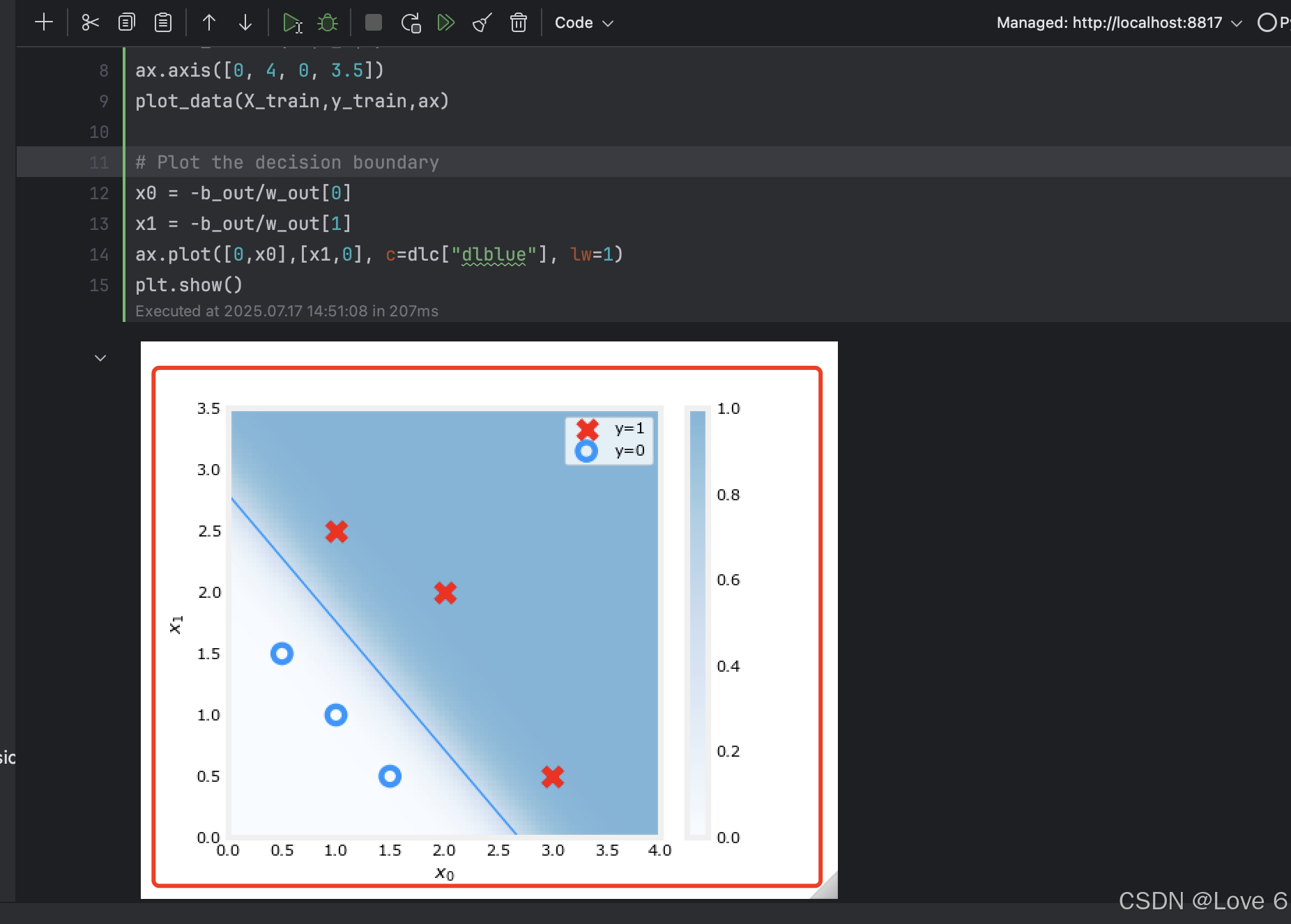
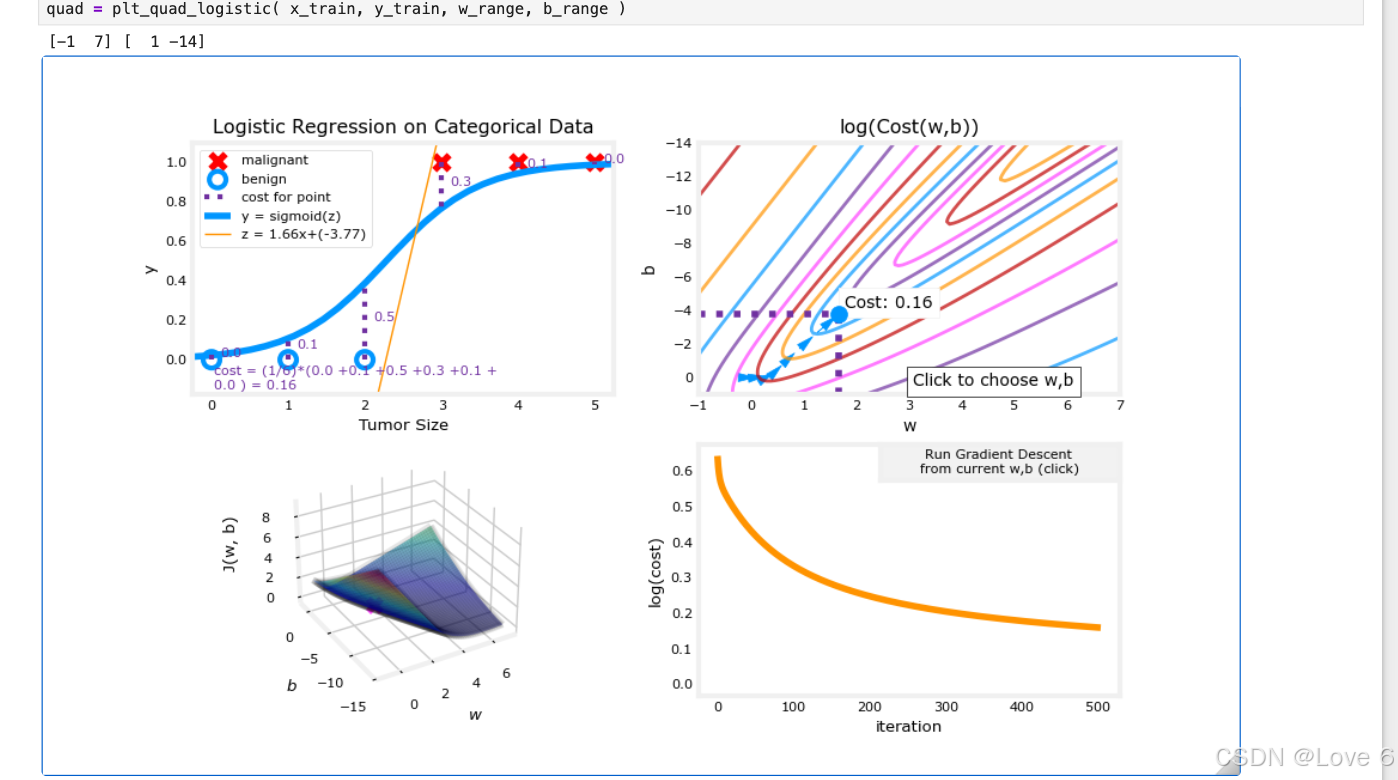
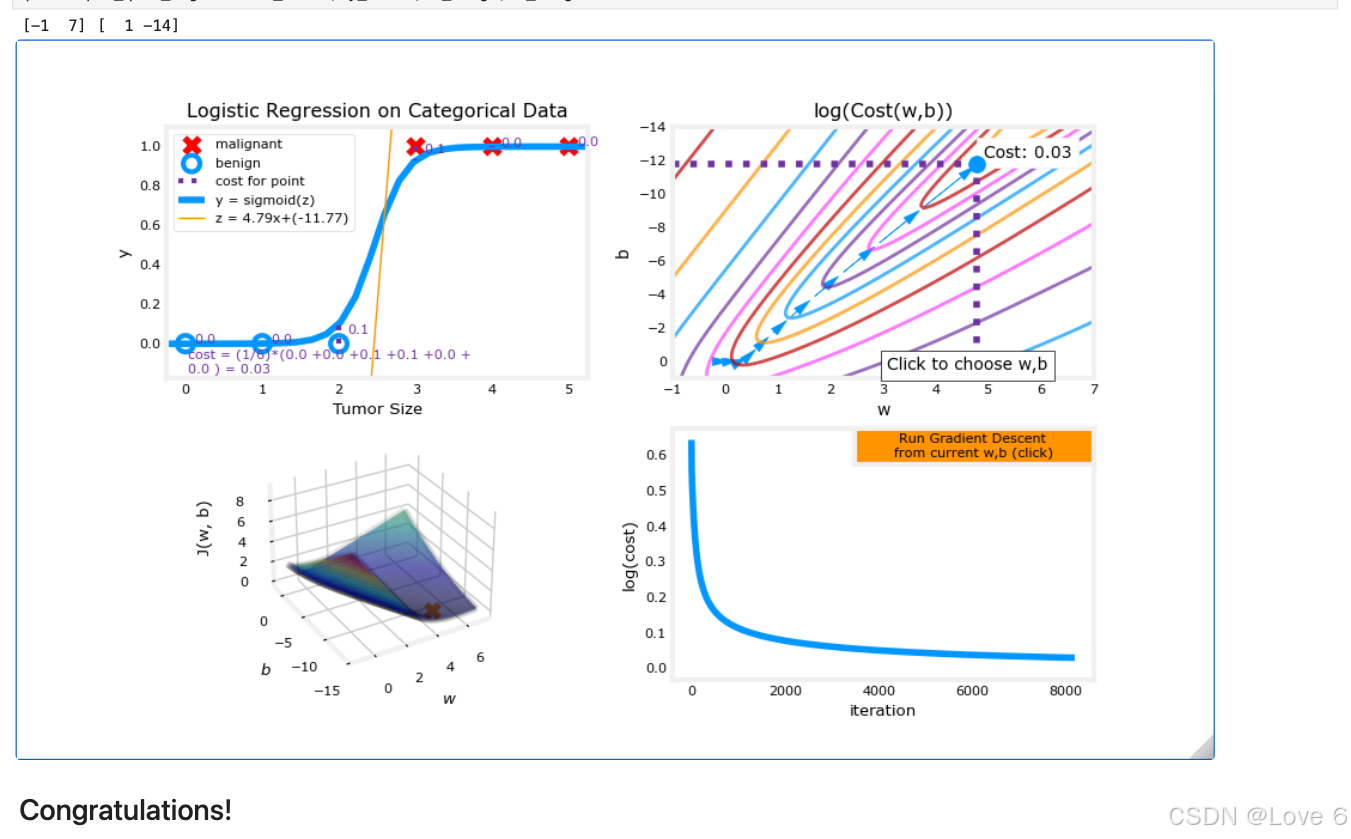
在这里插入图片描述

4、可视化 逻辑回归 Plot

这里就是给了一个可视化迭代的图 查看了一下函数变化的过程
还是很具体客观的

在这里插入图片描述

在这里插入图片描述

# 机器学习 # 逻辑回归
Logo
魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

cover

【计算机视觉】Pixel逐像素分类&Mask掩码分类理解摘要

avatar 魔乐社区

计算机视觉（opencv）实战三十二——CascadeClassifier 人脸微笑检测（摄像头）

本文从原理到实现，详细介绍了基于 OpenCV Haar 分类器的人脸与微笑检测：讲解了 Haar 特征和级联检测原理。对代码逐行拆解并解释参数含义。画出完整流程图，帮助理解执行过程。给出了常见问题和优化建议，甚至扩展到深度学习方法。这种方法简单、轻量、实时性好，非常适合入门和小型应用项目。但如果需要更高准确率和更强鲁棒性，建议使用深度学习检测器替代 Haar 分类器。

avatar 魔乐社区
cover

小杰机器学习（seven）——贝叶斯分类

avatar 魔乐社区