机器学习（四） 逻辑回归

1.什么是逻辑回归

逻辑回归（logistic regression)是用于分类的机器学习算法。
线性回归的输出是一个数值，而不是一个标签，显然不能直接解决二分类问题。一个最直观的办法就是设定一个阈值，比如0，如果我们预测的数值 y > 0 ，那么属于标签A，反之属于标签B。另一种方法，我们不去直接预测标签，而是去预测标签为A概率，我们知道概率是一个[0,1]区间的连续数值，那我们的输出的数值就是标签为A的概率。一般的如果标签为A的概率大于0.5，我们就认为它是A类，否则就是B类。

2. 通过Sigmoid函数进行转换

我们知道，概率是属于[0,1]区间。但是线性模型
$$f\left(x\right)=w^{T}x\text{的值域是}\left(-\infty ,+\infty \right)$$
所以我们不能直接基于线性模型建模。需要找到一个模型的值域刚好在[0,1]区间，同时要足够好用。

于是，选择了我们的sigmoid函数作为假设函数h(x),h(x)的值也就是逻辑回归算法所得到的y‘。
$$g\left(z\right)=\frac{1}{1+e^{-z}}$$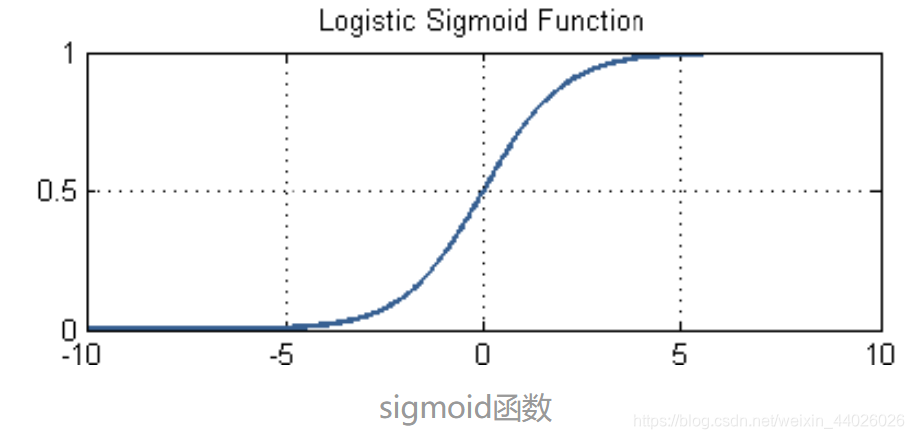

其中，z为中间变量：
$$z=w_0{x}_0+w_1{x}_1+...+w_n{x}_n=w^{T}X$$

3.逻辑回归的损失函数

损失函数就是用来衡量模型的输出与真实输出的差别。
不能采用MSE作为作为逻辑回归的损失函数，因为经过逻辑函数转换后，MSE对于w和b而言，不再是一个凸函数，这样的话就无法通过梯度下降找到一个全局最低点。所以定义新的损失函数：
$$\{\begin{array}{l}y=1,Loss\left(h\left(x\right),y\right)=-\log \left(h\left(x\right)\right)\\ y=0,Loss\left(h\left(x\right),y\right)=-\log \left(1-h\left(x\right)\right)\end{array}$$

• 如果真值为1，但假设函数预测概率接近0的话，得到的损失值是巨大的
• 如果真值为0，但假设函数预测概率接近1的话，得到的损失同样巨大

这种对于损失的惩罚力度是我们所期望的。
整合起来逻辑回归的惩罚函数如下：
$$L\left(w,b\right)=-\frac{1}{N}\sum \left[y\ast \log \left(h\left(x\right)\right)+\left(1-y\right)\ast \log \left(1-h\left(x\right)\right)\right]$$

4.逻辑回归的梯度下降

$$\text{梯度}=h^{\prime }\left(x\right)=\frac{\partial }{\partial w}L\left(w,b\right)=\frac{\partial }{\partial w}\left\{-\frac{1}{N}\sum \left[y\ast \log \left(h\left(x\right)\right)+\left(1-y\right)\ast \log \left(1-h\left(x\right)\right)\right]\right\}$$
省略运算得到：
$$\text{梯度}=\frac{1}{N}\sum _{i=1}^N\left(y^{\left(i\right)}-h\left(x^{\left(i\right)}\right)\right)\cdot x^{\left(i\right)}$$
参数随梯度变化而更新的公式如下：
$$w=w-\alpha \cdot \frac{\partial }{\partial w}L\left(w\right)$$
代码：

# 构建梯度下降的函数
def gradient_descent(X,y,w,b,lr,iter) : #定义逻辑回归梯度下降函数
    l_history = np.zeros(iter) # 初始化记录梯度下降过程中误差值(损失)的数组
    w_history = np.zeros((iter,w.shape[0],w.shape[1])) # 初始化权重记录的数组
    b_history = np.zeros(iter) # 初始化记录梯度下降过程中偏置的数组  
    for i in range(iter): #进行机器训练的迭代
        y_hat = sigmoid(np.dot(X,w) + b) #Sigmoid逻辑函数+线性函数(wX+b)得到y'
        loss = -(y*np.log(y_hat) + (1-y)*np.log(1-y_hat)) # 计算损失
        derivative_w = np.dot(X.T,((y_hat-y)))/X.shape[0]  # 给权重向量求导
        derivative_b = np.sum(y_hat-y)/X.shape[0] # 给偏置求导
        w = w - lr * derivative_w # 更新权重向量，lr即学习速率alpha
        b = b - lr * derivative_b   # 更新偏置，lr即学习速率alpha
        l_history[i] =  loss_function(X,y,w,b) # 梯度下降过程中的损失
        print ("轮次", i+1 , "当前轮训练集损失：",l_history[i]) 
        w_history[i] = w # 梯度下降过程中权重的历史 请注意w_history和w的形状
        b_history[i] = b # 梯度下降过程中偏置的历史
    return l_history, w_history, b_history

5.实例

5.1数据读入

import numpy as np # 导入NumPy数学工具箱
import pandas as pd # 导入Pandas数据处理工具箱
df_heart = pd.read_csv("C:/Users/aaa/Desktop/python/data/heart.csv")  # 读取文件
df_heart.head() # 显示前5行数据

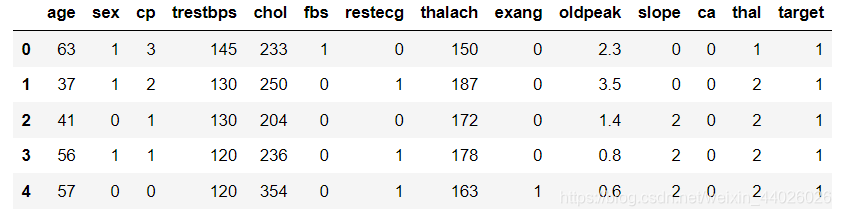
df_heart.target.value_counts() # 输出分类值，及各个类别数目

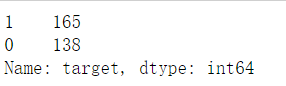
import matplotlib.pyplot as plt # 导入绘图工具
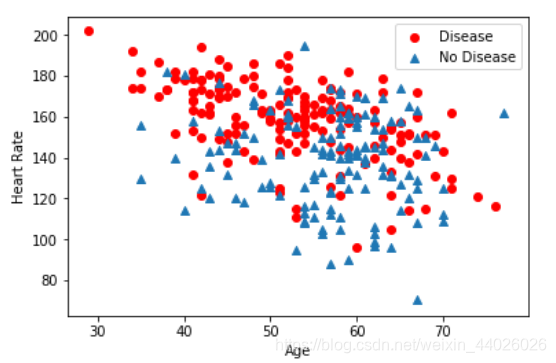
# 以年龄+最大心率作为输入，查看分类结果散点图
plt.scatter(x=df_heart.age[df_heart.target==1],
            y=df_heart.thalach[(df_heart.target==1)], c="red")
plt.scatter(x=df_heart.age[df_heart.target==0],
            y=df_heart.thalach[(df_heart.target==0)], marker='^')
plt.legend(["Disease", "No Disease"]) # 显示图例
plt.xlabel("Age") # X轴-Age
plt.ylabel("Heart Rate") # Y轴-Heart Rate
plt.show() # 显示散点图

对于cp字段，表示胸痛类型，取值0，1，2，3只表示分类，无关大小。如果以0，1，2，3这样取值，计算机会认为3比2大，2比1大，这样会导致误判。

所以解决的方法是把这种类别特征拆分为哑变量，比如cp有4类，那么cp_0,cp_1,cp_2,cp_3就表示4个特征，每个特征都还原为二元分类，答案是yes或者no，也就是1或者0.

# 把3个文本型变量转换为哑变量
a = pd.get_dummies(df_heart['cp'], prefix = "cp")
b = pd.get_dummies(df_heart['thal'], prefix = "thal")
c = pd.get_dummies(df_heart['slope'], prefix = "slope")
# 把哑变量添加进dataframe
frames = [df_heart, a, b, c]
df_heart = pd.concat(frames, axis = 1)
df_heart = df_heart.drop(columns = ['cp', 'thal', 'slope'])
df_heart.head() # 显示新的dataframe

5.2 构建特征集和标签集

X = df_heart.drop(['target'], axis = 1) # 构建特征集
y = df_heart.target.values # 构建标签集
y = y.reshape(-1,1) # -1是	相对索引，等价于len(y)
print("张量X的形状:", X.shape)
print("张量X的形状:", y.shape)

5.3 拆分数据集

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = 0.2)

5.4 特征缩放

from sklearn.preprocessing import MinMaxScaler # 导入数据缩放器
scaler = MinMaxScaler() # 选择归一化数据缩放器，MinMaxScaler
X_train = scaler.fit_transform(X_train) # 特征归一化 训练集fit_transform
X_test = scaler.transform(X_test) # 特征归一化 测试集transform

5.5 建立逻辑回归模型

# 首先定义一个Sigmoid函数，输入Z，返回y'
def sigmoid(z):    
    y_hat = 1/(1+ np.exp(-z))
    return y_hat    

# 然后定义损失函数
def loss_function(X,y,w,b):
    y_hat = sigmoid(np.dot(X,w) + b) # Sigmoid逻辑函数 + 线性函数(wX+b)得到y'
    loss = -(y*np.log(y_hat) + (1-y)*np.log(1-y_hat)) # 计算损失
    cost = np.sum(loss) / X.shape[0]  # 整个数据集平均损失    
    return cost # 返回整个数据集平均损失

# 然后构建梯度下降的函数
def gradient_descent(X,y,w,b,lr,iter) : #定义逻辑回归梯度下降函数
    l_history = np.zeros(iter) # 初始化记录梯度下降过程中误差值(损失)的数组
    w_history = np.zeros((iter,w.shape[0],w.shape[1])) # 初始化权重记录的数组
    b_history = np.zeros(iter) # 初始化记录梯度下降过程中偏置的数组  
    for i in range(iter): #进行机器训练的迭代
        y_hat = sigmoid(np.dot(X,w) + b) #Sigmoid逻辑函数+线性函数(wX+b)得到y'
        loss = -(y*np.log(y_hat) + (1-y)*np.log(1-y_hat)) # 计算损失
        derivative_w = np.dot(X.T,((y_hat-y)))/X.shape[0]  # 给权重向量求导
        derivative_b = np.sum(y_hat-y)/X.shape[0] # 给偏置求导
        w = w - lr * derivative_w # 更新权重向量，lr即学习速率alpha
        b = b - lr * derivative_b   # 更新偏置，lr即学习速率alpha
        l_history[i] =  loss_function(X,y,w,b) # 梯度下降过程中的损失
        print ("轮次", i+1 , "当前轮训练集损失：",l_history[i]) 
        w_history[i] = w # 梯度下降过程中权重的历史 请注意w_history和w的形状
        b_history[i] = b # 梯度下降过程中偏置的历史
    return l_history, w_history, b_history

def predict(X,w,b): # 定义预测函数
    z = np.dot(X,w) + b # 线性函数
    y_hat = sigmoid(z) # 逻辑函数转换
    y_pred = np.zeros((y_hat.shape[0],1)) # 初始化预测结果变量  
    for i in range(y_hat.shape[0]):
        if y_hat[i,0] < 0.5:
            y_pred[i,0] = 0 # 如果预测概率小于0.5，输出分类0
        else:
            y_pred[i,0] = 1 # 如果预测概率大于0.5，输出分类0
    return y_pred # 返回预测分类的结果

def logistic_regression(X,y,w,b,lr,iter): # 定义逻辑回归模型
    l_history,w_history,b_history = gradient_descent(X,y,w,b,lr,iter)#梯度下降
    print("训练最终损失:", l_history[-1]) # 打印最终损失
    y_pred = predict(X,w_history[-1],b_history[-1]) # 进行预测
    traning_acc = 100 - np.mean(np.abs(y_pred - y_train))*100 # 计算准确率
    print("逻辑回归训练准确率: {:.2f}%".format(traning_acc))  # 打印准确率
    return l_history, w_history, b_history # 返回训练历史记录

#初始化参数
dimension = X.shape[1] # 这里的维度 len(X)是矩阵的行的数，维度是列的数目
weight = np.full((dimension,1),0.1) # 权重向量，向量一般是1D，但这里实际上创建了2D张量
bias = 0 # 偏置值
#初始化超参数
alpha = 1 # 学习速率
iterations = 500 # 迭代次数

# 用逻辑回归函数训练机器
loss_history, weight_history, bias_history =  \
            logistic_regression(X_train,y_train,weight,bias,alpha,iterations)

y_pred = predict(X_test,weight_history[-1],bias_history[-1]) # 预测测试集
testing_acc = 100 - np.mean(np.abs(y_pred - y_test))*100 # 计算准确率
print("逻辑回归测试准确率: {:.2f}%".format(testing_acc))

loss_history_test = np.zeros(iterations) # 初始化历史损失
for i in range(iterations): #求训练过程中不同参数带来的测试集损失
    loss_history_test[i] = loss_function(X_test,y_test,
                                         weight_history[i],bias_history[i])
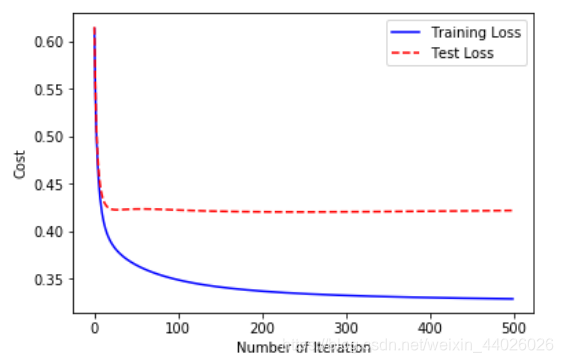
index = np.arange(0,iterations,1)
plt.plot(index, loss_history,c='blue',linestyle='solid')
plt.plot(index, loss_history_test,c='red',linestyle='dashed')
plt.legend(["Training Loss", "Test Loss"])
plt.xlabel("Number of Iteration")
plt.ylabel("Cost")
plt.show() # 同时显示显示训练集和测试集损失曲线