机器学习(三)多项式回归
多项式回归模型的原理、建模、调优以及预测
·
一、原理
原型公式:
与多项式回归的区别:仅有一个自变量,次方数不同
适用情况:
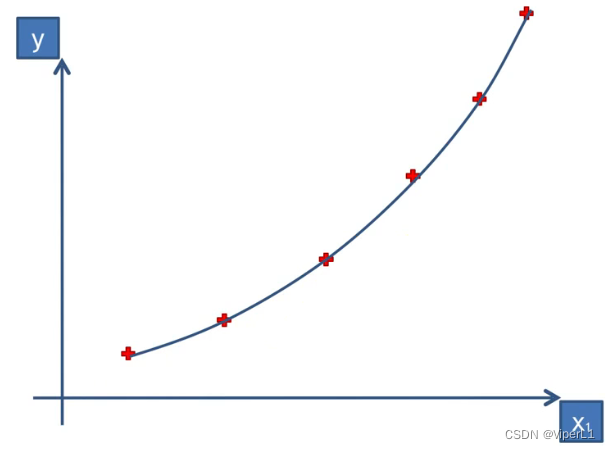
属于线性回归的原因:线性并不是对于图线而言,是对于y是否能由自变量线性表达。
二、Python处理
从模型角度:多项式回归为非线性模型
①设置工作路径
②数据预处理
③多项式回归模型的建立和拟合
--用于参照的线性回归模型
from sklearn.Liner_model import LinearRegession
Lin_reg=LinearRegression() --线性回归对象
Lin_reg.fit(x,y) --拟合
--多项式回归模型
--矩阵转换
from sklearn.preprocessing import PoltnomialFeatures
poly_reg = PolnomialFeatures(degeree=2) --用于将自变量替换为其更高阶的矩阵(示例为2次)
x_poly = poly_reg.fit_transform(x) --转换
--模型构造
lin_reg_2 = LinearRegression()
Lin_reg_2.fit(x_poly,y)
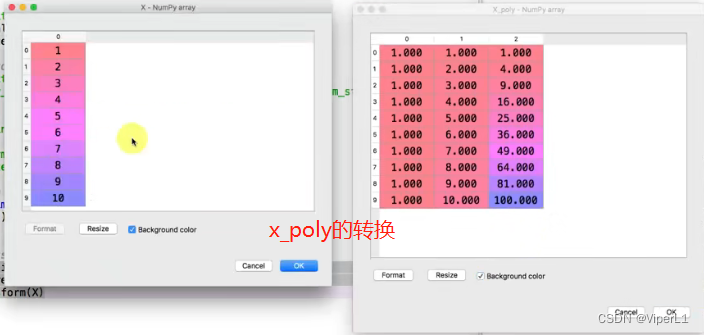
--绘制模型
plt.sactter(x,y,color='red') --绘点
plt.plot(x,lin_reg.predict(x),color='blue') --线性回归图像
plt.title('真假?(线性模型)')
plt.xlabel('职位水平')
plt.ylabel('薪水')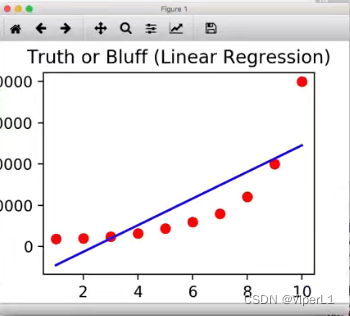
--绘制模型
plt.sactter(x,y,color='red') --绘点
plt.plot(x,lin_reg_2.predict(poly_reg.fit_transform(x)),color='blue')
--多项式回归图像
plt.title('真假?(多项式模型)')
plt.xlabel('职位水平')
plt.ylabel('薪水')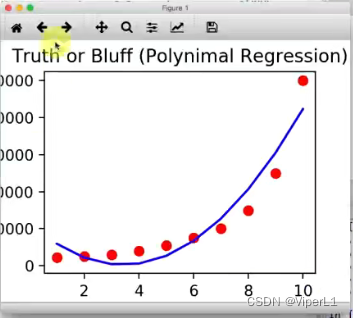
模拟结果已经好了很多,但是拟合度还有待提高。可以通过升高多项式的次数来提升拟合度
poly_reg = PolnomialFeatures(degeree=4) --模型次数升高为4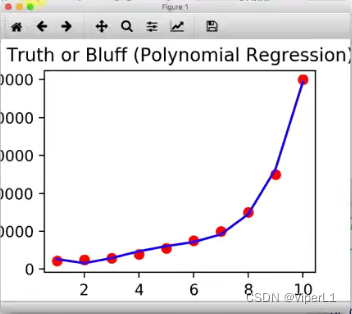
由于x轴间距过大,导致图像不够平缓,可以通过缩小点间距使得图像更为平整
x_grid = np.arange(min(x),max(x),0.1) --最小值、最大值、步距
x_grid = x_grid.reshape(len(x_grid),1) --转换为矩阵
--绘制模型
plt.sactter(x,y,color='red') --绘点
plt.plot(x_grid,lin_reg_2.predict(poly_reg.fit_transform(x_grid)),color='blue')
--多项式回归图像
plt.title('真假?(多项式模型)')
plt.xlabel('职位水平')
plt.ylabel('薪水')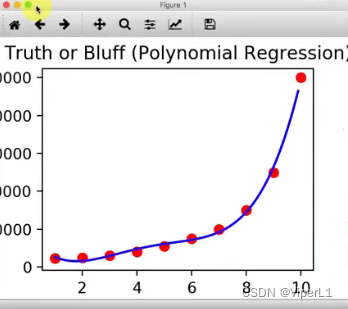
④进行预测
lin_reg.predict(6.5) --线性模型预测
--误差较大
lin_reg_2.predict(poly_reg.fit_transform(6.5))
--误差较小
魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献7条内容
已为社区贡献7条内容







所有评论(0)