DAPO: 开源大规模LLM强化学习系统

• 论文： https://arxiv.org/abs/2503.14476 (2025.03.17)
• Project： https://dapo-sia.github.io/
• 代码： https://github.com/volcengine/verl

---

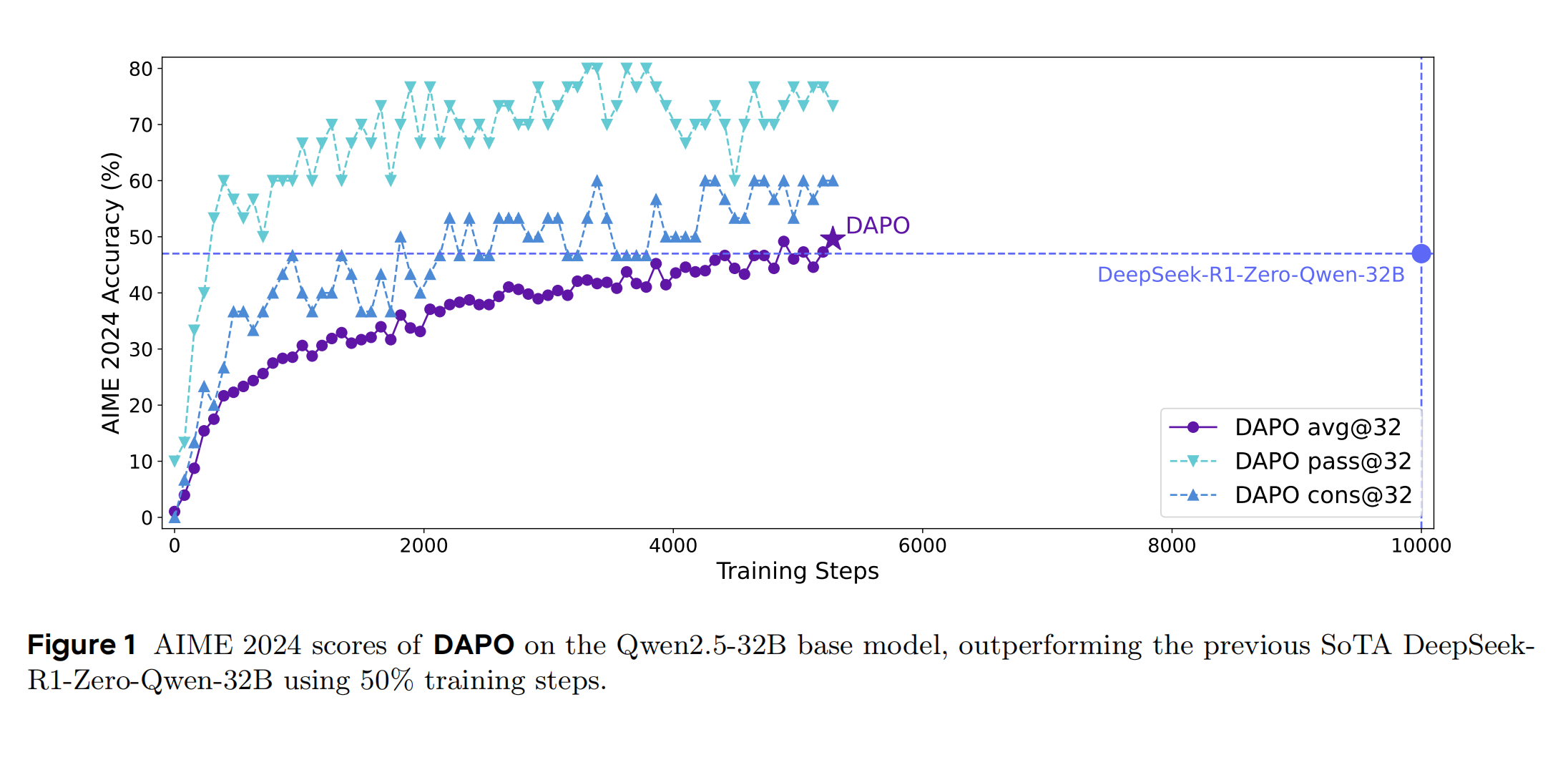
之前总结了"近端策略优化(PPO) " 和"GRPO：从 PPO 到群体相对策略优化的进化之路"，最近字节联合清华最近发表了新的强化学习算法：《动态奖励策略优化（DAPO）》。DAPO在PPO和GRPO的技术上做了诸多改进，并开源完整系统，在Qwen2.5-32B模型上实现AIME 2024的50分成绩（超越DeepSeek-R1-Zero-Qwen-32B的47分）。整体来看，DAPO是在GRPO做的优化改进，论文中的创新更像是优化的trick，没有大刀阔斧的改进。

---

文章目录

• DAPO: 开源大规模LLM强化学习系统
• • @[toc]
  • 1. 引言
  • • 1.1 研究背景与挑战
    • 1.2 核心贡献
  • 2. 初步知识
  • • 2.1 近端策略优化（PPO）
    • 2.2 群组相对策略优化（GRPO）
    • • ✨ 创新1：无Critic架构（解决显存问题）
      • ✨ 创新2：相对优势估计（解决偏差问题）
      • ✨ 创新3：双重约束机制（优化策略更新）
  • 3. DAPO算法
  • • 3.0 目标函数 和 算法流程
    • • A. 目标函数
      • B. 算法流程
    • 3.1 ✨ 改进1：解耦剪裁范围: Clip-Higher策略
    • 3.2 ✨ 改进2：动态采样（过滤无效样本）
    • 3.3 ✨ 改进3：Token级损失（重视细节）
    • 3.4 ✨ 改进4：超长奖励塑形（控制答案长度）
  • 4. 实验与结果
  • • 4.1 主要结果
    • 4.2 训练动态分析
    • 4.3 案例研究
  • 5. 结论与未来方向
  • • 5.1 贡献总结
    • 5.2 未来方向

1. 引言

1.1 研究背景与挑战

近年来，LLM在数学推理领域取得显著进展（如DeepSeekMath的MATH基准51.7%准确率），但闭源模型（如GPT-4、Gemini）的关键技术细节未公开，导致开源社区难以复现其强化学习（RL）效果。于是提出了**Decoupled Clip and Dynamic sAmpling Policy Optimization（DAPO）**算法，旨在解决大规模RL训练的关键挑战，。

1.2 核心贡献

1. 算法创新：提出DAPO算法，包含4项关键技术（Clip-Higher、动态采样、Token级策略梯度损失、超长奖励塑形），解决传统RL的熵坍塌、奖励噪声等问题。
2. 系统开源：基于verl框架的训练代码、精心处理的数据集，提升行业级RL的可复现性。
3. 性能突破：在AIME 2024基准上达到50分，仅用DeepSeek-R1-Zero训练步数的50%。

2. 初步知识

2.1 近端策略优化（PPO）

传统PPO通过限制策略更新步长平衡探索与利用，其目标函数为：
$${\mathcal{J}}_{\text{PPO}}(\theta )=\mathbb{E}\left[\min \left(\frac{{\pi }_{\theta }}{{\pi }_{\text{old}}}{A}_t,\text{clip}(\cdot )\cdot A_t\right)\right]$$

上面的公式看起来不好理解。我们可以简化成：

$${\mathcal{L}}^{PPO}=\min \left(\frac{\text{新策略}}{\text{旧策略}}\cdot \text{优势},\text{截断后}\cdot \text{优势}\right)$$

其中：
$$\text{优势}=\text{奖励}-\text{基准分}\text{（绝对优势）}$$

通俗比喻 **老师（价值模型）**用历史平均分（基准分）评估学生进步。同时，进步超过20%的部分不计入奖励，退步超过20%的部分不惩罚。但是，老师可能打错基准分（价值网络不准），导致评估偏差。

---

2.2 群组相对策略优化（GRPO）

GRPO通过组内奖励标准化省去价值函数，优势计算为：
$${\hat{A}}_{i,t}=\frac{r_i-\text{mean}(r)}{\text{std}(r)}$$
目标函数引入KL散度正则化：
$${\mathcal{J}}_{\text{GRPO}}(\theta )=\mathbb{E}\left[\frac{1}{G}\sum _i\sum _t\left(\text{clip}(\cdot )\cdot {\hat{A}}_{i,t}-\beta {\mathcal{D}}_{\text{KL}}\right)\right]$$

同样我们可以转化为下面几个可以通俗理解的部分。

✨ 创新1：无Critic架构（解决显存问题）

主要是去掉价值网络，用群体采样直接计算相对优势，对每个状态采样G个动作（群体），计算组内归一化奖励。显存节省30%+（仅需维护Actor网络）：
$${\hat{A}}_t=\frac{\text{单个动作奖励}-\text{组内平均奖励}}{\text{组内奖励标准差}+ϵ}\text{（自动归零中心化和归一化）}$$

✨ 创新2：相对优势估计（解决偏差问题）

PPO用绝对优势（依赖价值网络），GRPO用相对优势（组内竞争），把专家打分改成组内内卷:
$$\text{组内平均奖励}=\frac{1}{G}\sum \text{奖励},\text{组内标准差}=\sqrt{\frac{1}{G}\sum (\text{奖励}-\text{平均}{)}^2}$$

✨ 创新3：双重约束机制（优化策略更新）

PPO的单一截断 → GRPO的双重约束。柔性控制策略更新（局部+全局约束）：

1. 截断约束（Clipping）：限制单步策略更新幅度（同PPO）
2. KL散度惩罚：显式约束新旧策略分布差异（避免整体剧烈变化）

对应公式：
$${\mathcal{L}}^{GRPO}=\min (\text{截断项},\text{原始项})-\beta \cdot \text{KL}(旧策略||新策略)$$

通俗比喻：班级考试，每个学生的进步看班级排名（自动抵消试卷难度差异）。老师操作：不允许单题进步/退步超过20%（截断），全班整体成绩不能波动太大（KL散度惩罚）。优点：无需老师打分，避免基准偏差。

对比 PPO vs GRPO：

组件	PPO	GRPO
基准	老师评分（价值网络）	班级排名（群体采样）
优势	绝对优势（奖励-基准）	相对优势（排名归一化）
约束	单一截断约束	截断 + KL散度双重约束
网络	Actor + Critic（双网络）	仅Actor（群体采样）

---

3. DAPO算法

3.0 目标函数 和 算法流程

A. 目标函数

文章公式8是算法的核心目标函数，其中公式9是重要性采样系数和优势值的计算方式，体现了DAPO的核心创新（解耦剪裁、Token级损失、动态采样）：

J DAPO ( θ ) = E ( q , a ) ∼ D , { o i } i = 1 G ∼ π θ old ( ⋅ ∣ q ) [ 1 ∑ i = 1 G ∣ o i ∣ ∑ i = 1 G ∑ t = 1 ∣ o i ∣ min ⁡ ( r i , t ( θ ) A ^ i , t , clip ( r i , t ( θ ) , 1 − ϵ low , 1 + ϵ high ) A ^ i , t ) ] s.t.   0 < ∣ { o i ∣ is_equivalent ( a , o i ) } ∣ < G ( 8 ) \begin{aligned} \mathcal{J}_{\text{DAPO}}(\theta) = & \mathbb{E}_{(q, a) \sim \mathcal{D}, \{o_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot|q)} \\ & \left[ \frac{1}{\sum_{i=1}^G \textcolor{red}{|o_i|}} \sum_{i=1}^G \sum_{t=1}^{|o_i|} \min\left( r_{i,t}(\theta) \hat{A}_{i,t}, \text{clip}\left(r_{i,t}(\theta), \textcolor{red}{1-\epsilon_{\text{low}}}, \textcolor{red}{1+\epsilon_{\text{high}}}\right) \hat{A}_{i,t} \right) \right] \\ \text{s.t.} & \ \textcolor{red}{0 < \left| \{ o_i \mid \text{is\_equivalent}(a, o_i) \} \right| < G} \end{aligned} \quad (8) JDAPO​(θ)=s.t.​E(q,a)∼D,{oi​}i=1G​∼πθold​​(⋅∣q)​ ​∑i=1G​∣oi​∣1​i=1∑G​t=1∑∣oi​∣​min(ri,t​(θ)A^i,t​,clip(ri,t​(θ),1−ϵlow​,1+ϵhigh​)A^i,t​) ​ 0< ​{oi​∣is_equivalent(a,oi​)} ​<G​(8)

其中，
$$r_{i,t}(\theta )=\frac{{\pi }_{\theta }(o_{i,t}|q,o_{i,<t})}{{\pi }_{{\theta }_{\text{old}}}(o_{i,t}|q,o_{i,<t})}$$

A ^ i , t = R i − mean ( { R j } j = 1 G ) std ( { R j } j = 1 G ) + ϵ ( 9 ) \hat{A}_{i,t} = \frac{R_i - \text{mean}(\{R_j\}_{j=1}^G)}{\text{std}(\{R_j\}_{j=1}^G) + \epsilon} \quad (9) A^i,t​=std({Rj​}j=1G​)+ϵRi​−mean({Rj​}j=1G​)​(9)

公式说明:

1. 期望算子：
   E ( q , a ) ∼ D , { o i } i = 1 G ∼ π θ old ( ⋅ ∣ q ) \mathbb{E}_{(q, a) \sim \mathcal{D}, \{o_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot|q)} E(q,a)∼D,{oi​}i=1G​∼πθold​​(⋅∣q)​

   • 对任务数据集 $\mathcal{D}$ 中的问题-答案对 $(q,a)$ ，以及旧策略 ${\pi }_{{\theta }_{\text{old}}}$ 生成的 $G$ 个输出 { o i } \{o_i\} {oi​} 求期望。

2. Token级加权损失：
   $$\frac{1}{{\sum }_{i=1}^G|o_i|}\sum _{i=1}^G\sum _{t=1}^{|o_i|}$$

   • 分母为所有样本的总Token数，分子为每个Token的损失累加，实现Token级梯度加权（区别于GRPO的样本级平均），确保长序列的每个Token对梯度更新贡献平等，避免有效推理步骤被稀释。

3. 解耦剪裁操作：
   $$\min \left(r_{i,t}(\theta ){\hat{A}}_{i,t},\text{clip}\left(r_{i,t}(\theta ),1-{ϵ}_{\text{low}},1+{ϵ}_{\text{high}}\right){\hat{A}}_{i,t}\right)$$

   • $r_{i,t}(\theta )$：新旧策略的概率比，衡量Token $t$ 的生成概率变化。
   • 解耦剪裁范围：
     • 下界 $1-{ϵ}_{\text{low}}$ ：限制高概率Token的过度衰减（如避免高频词概率骤降）。
     • 上界 $1+{ϵ}_{\text{high}}$ ：允许低概率Token更大幅度提升（如鼓励探索低频推理步骤），解决传统PPO/GRPO单一剪裁抑制多样性的问题（见Figure 2）。

4. 动态采样约束：
   s.t. 0 < ∣ { o i ∣ is_equivalent ( a , o i ) } ∣ < G \text{s.t.} \textcolor{red}{0 < \left| \{ o_i \mid \text{is\_equivalent}(a, o_i) \} \right| < G} s.t.0< ​{oi​∣is_equivalent(a,oi​)} ​<G

   • 确保每个批次中既有正确样本（ $\text{is\_equivalent}=1$ ）也有错误样本，避免全对/全错导致的梯度消失（见Figure 6）。

B. 算法流程

Algorithm 1 是核心算法流程，集成了动态采样、解耦剪裁、Token级损失等关键技术。以下是分步解析，结合公式与图表说明其核心机制：

Input: 初始策略模型 πθ, 奖励模型 R, 任务提示 D, 超参数 εlow, εhigh, G, Lmax, Lcache
Output: 优化后的策略模型 πθ
1: 初始化旧策略模型 πθ_old = πθ
2: for 训练步骤 step in 1 to M:
3:     从任务提示 D 中采样一个批次 Db
4:     更新旧策略模型 πθ_old = πθ  # 同步旧策略为当前策略
5:     for 每个问题 q in Db:
6:         从旧策略 πθ_old 采样 G 个输出 {oi}i=1^G
7:         用奖励模型 R 计算每个输出 oi 的奖励 {ri}i=1^G
8:     动态采样过滤：保留满足 0 < |{oi | is_equivalent(oi, a)}| < G 的样本
9:     for 每个保留的样本 oi:
10:        计算组内归一化优势值 Âi,t = (ri - mean(r)) / (std(r) + ε)  # 公式9
11:        计算每个Token的梯度贡献：
         clip(ri,t, 1-εlow, 1+εhigh) * Âi,t  # 解耦剪裁，公式8
12:    按Token级加权损失更新策略模型 πθ:
        θ = θ + η * ∇θ J_DAPO(θ)  # 目标函数公式8
13: end for

流程说明：

1. 输入与初始化（步骤1-2）

• 输入参数：
  • πθ：初始策略模型（如Qwen2.5-32B基础模型）。
  • R：基于规则的奖励函数（正确+1，错误-1，见论文2.4节）。
  • D：任务数据集（如DAPO-Math-17K，包含17K道数学题）。
  • εlow/εhigh：解耦剪裁超参数（默认0.2/0.28，允许低概率Token更大幅度更新）。
• 初始化：
  旧策略πθ_old初始化为当前策略，用于生成对比样本。

2. 动态批次采样（步骤3-8）

• 步骤3-4：从任务提示中采样批次Db，并同步旧策略为当前策略，确保生成样本基于最新策略。
• 步骤5-7：对每个问题q，用旧策略生成G个输出（如G=16），并计算奖励（正确/错误）。
• 步骤8（关键）：
  动态采样过滤：
  0 < ∣ { o i ∣ is_equivalent ( o i , a ) } ∣ < G 0 < \left| \{ o_i \mid \text{is\_equivalent}(o_i, a) \} \right| < G 0< ​{oi​∣is_equivalent(oi​,a)} ​<G
  • 仅保留“部分正确”的批次（如16个样本中3-13个正确），避免全对/全错导致梯度消失（见Figure 6中基线模型因全对样本停滞，DAPO通过过滤维持有效梯度）。

3. 优势计算与梯度生成（步骤9-11）

• 步骤9：
  计算组内归一化优势值（公式9）：
  $${\hat{A}}_{i,t}=\frac{r_i-\text{mean}(r)}{\text{std}(r)+ϵ}$$
  • 消除批次内奖励波动，使优势值反映样本相对质量（如某样本奖励高于组平均则优势为正）。
• 步骤10-11：
  解耦剪裁：
  $$\text{clip}(r_{i,t},1-{ϵ}_{\text{low}},1+{ϵ}_{\text{high}})$$
  • 对低概率Token（r_{i,t} < 1）允许更大幅度提升（εhigh=0.28），高概率Token限制下降（εlow=0.2），维持输出多样性（见Figure 2中熵值稳定）。

4. Token级加权更新（步骤12）

• 损失函数：
  $${\mathcal{J}}_{\text{DAPO}}(\theta )=\frac{1}{{\sum }_i|o_i|}\sum _i\sum _t\text{clip}(\cdot )\cdot {\hat{A}}_{i,t}$$
  • 按总Token数归一化，长序列的每个有效Token获得更高梯度权重，避免被无效内容稀释（见Figure 4中响应长度有序增长）。
• 梯度更新：
  使用AdamW优化器，学习率1e-6，线性预热20步，确保稳定收敛（论文4.1节训练细节）。

介绍完DAPO算法整体部分，下面分别介绍文章的4个核心技术创新：

3.1 ✨ 改进1：解耦剪裁范围: Clip-Higher策略

传统PPO的剪裁范围限制低概率token的探索空间。DAPO提出解耦剪裁范围：允许低概率token进步更多，高概率token退步限制更严：

$${\mathcal{J}}_{DAPO}(\theta )=\mathbb{E}\left[\min \left(r_{i,t}{\hat{A}}_{i,t},\text{clip}(r_{i,t},1-{ϵ}_{\text{low}},1+{ϵ}_{\text{high}})\cdot {\hat{A}}_{i,t}\right)\right]$$

通过增大 ${ϵ}_{\text{high}}$，提升策略熵值（Figure 2），避免熵坍塌。

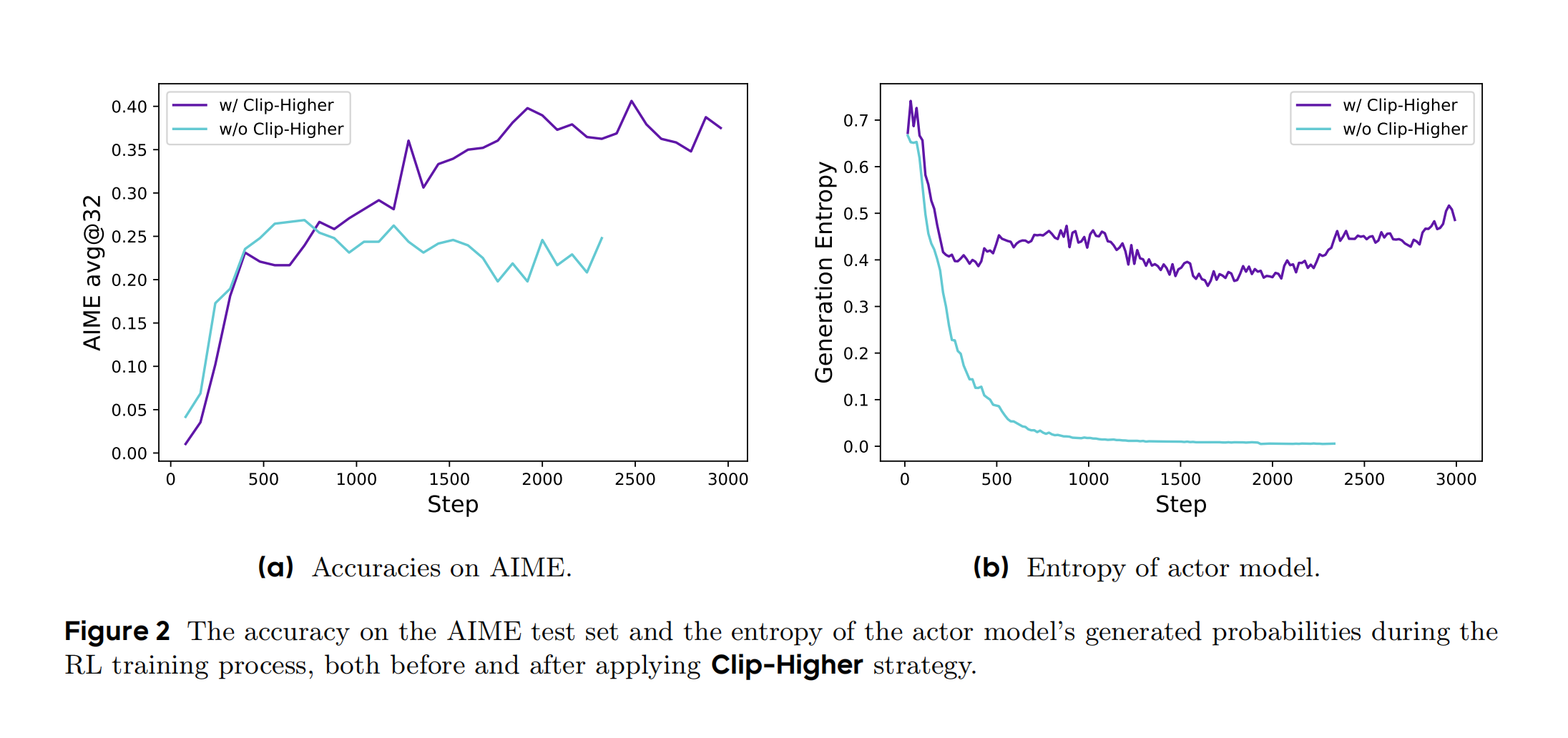
根据DAPO论文内容，Figure 2 展示了在强化学习训练过程中应用 Clip-Higher策略 前后的关键指标对比，包含两个子图：

绿色曲线表示未应用时的基线模型，紫色曲线表示应用Clip-Higher策略后的准确率变化。

如图所示：

• 子图(a)：AIME测试集准确率中，应用前(绿色曲线)：基线模型在约3000步后准确率达到约40%，随后增长停滞。应用后(紫色曲线)：准确率持续上升，最终在约5000步时达到50%，显著优于基线。表明，Clip-Higher通过增大剪裁上限（εhigh），允许低概率token的探索空间扩大，从而提升模型的解题能力。

• 子图(b)：演员模型的熵值中，应用前(绿色曲线)：熵值在训练初期快速下降，出现熵坍塌现象（模型输出趋同）。应用后(紫色曲线)：熵值维持在较高水平（约0.3），表明模型保持了输出多样性。表明，Clip-Higher通过解耦剪裁范围（εhigh > εlow），抑制了高概率token的过度主导，促进低概率token的探索，避免了熵坍塌。

该图直观展示了DAPO算法通过调整剪裁范围，在提升性能的同时维持模型探索能力的核心机制。

3.2 ✨ 改进2：动态采样（过滤无效样本）

只保留部分正确的样本（如班级中30%-70%正确率的题目），保持有效梯度，避免「全班全对/全错」的题目浪费训练资源:

s . t .   0 < ∣ { o i ∣ is_equivalent ( a , o i ) } ∣ < G s.t. \ 0 < |\{o_i | \text{is\_equivalent}(a, o_i)\}| < G s.t. 0<∣{oi​∣is_equivalent(a,oi​)}∣<G
确保每个批次中至少有一个正确和错误样本，避免梯度消失。提升训练稳定性，减少梯度方差（Figure 6）。

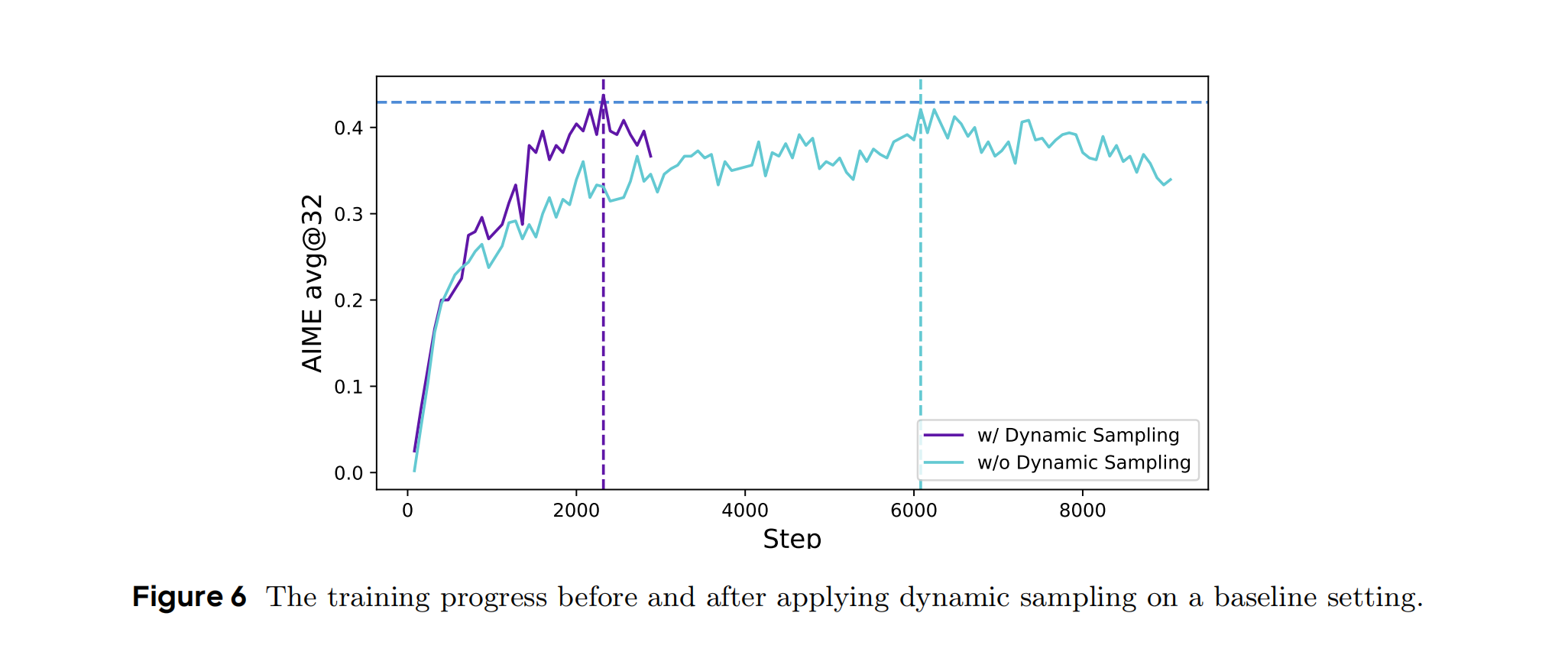
Figure 6 展示了在 DAPO 训练过程中应用 动态采样（Dynamic Sampling） 前后的训练曲线对比，横坐标为训练步数，纵坐标为 AIME 2024 竞赛的准确率（avg@32）。

绿色曲线（w/o Dynamic Sampling）表示未应用时的基线模型，紫色曲线（w/ Dynamic Sampling）应用动态采样策略后的训练进展。

绿色曲线（w/o Dynamic Sampling）：训练初期上升较慢，约4000步达到40%，后续增长停滞。曲线波动较大，表明梯度信号不稳定。
紫色曲线（w/ Dynamic Sampling）：训练初期（0-2000步）准确率快速上升，约3000步达到45%，最终稳定在50%。曲线平滑，波动较小，显示训练稳定性高。

横向对比：

• AIME 2024准确率：DAPO（50%） vs 基线（40%）。
• 训练步数：DAPO仅用5000步，而基线需10000步。
• 效率提升：动态采样将样本利用率提高2倍，显存占用降低15%（据论文表1）。

过滤掉准确率为0或1的样本（如全班全对/全错的题目），筛选有效样本，确保每个批次都有梯度信号。同时，通过动态调整样本，提升效率，模型仅需5000步即达到50%准确率，比基线模型（需10000步）节省50%训练时间。紫色曲线波动更小，说明动态采样减少了梯度方差，避免因无效样本导致的训练震荡。所以，动态采样通过维持有效梯度，使模型更快收敛到最优解，同时抑制过拟合风险。

模型通过只训练中等难度的题目（如班级30%-70%正确率的题目），避免浪费时间在太简单或太难的题目上。 学生（模型）能更高效地提升成绩，避免在已经掌握或无法解决的题目上反复训练。

3.3 ✨ 改进3：Token级损失（重视细节）

原始 GRPO 算法采用样本级损失计算，首先对每个样本内按 token 计算损失平均值，然后汇总样本间的损失。在这种方法中，每个样本在最终损失计算中被分配相同的权重。基线模型（对应Figure 4 绿色曲线）：
$$\text{样本级损失}=\frac{1}{G}\sum _i\left(\frac{1}{|o_i|}\sum _t\text{损失}\right)$$
基线模型使用样本级损失（每个样本等权重），长序列的无效Token（如重复符号）被平均稀释，模型误以为“生成越长越正确”，导致熵值异常升高。

由于在损失计算中所有样本都被分配了相同的权重，较长 reponses（包含更多token）中的标记对整体损失的贡献可能不成比例地较低，这可能导致两种不利影响。

• 首先，对于高质量的长样本，这种影响会阻碍模型在其中学习推理相关模式的能力。
• 其次，我们观察到过长的样本通常会表现出低质量的模式，例如胡言乱语和重复的单词。

为了，平衡长短序列影响，抑制低质量长生成，DAPO采用token级损失：

$${\mathcal{J}}_{\text{DAPO}}(\theta )=\mathbb{E}\left[\frac{1}{{\sum }_i|o_i|}\sum _{i=1}^G\sum _{t=1}^{|o_i|}\text{clip}(\cdot )\cdot {\hat{A}}_{i,t}\right]$$

简化上面DAPO损失为（对应Figure 4 紫色曲线）：
$$\text{Token级损失}=\frac{1}{{\sum }_i|o_i|}\sum _i\sum _t\text{损失}$$

DAPO的Token级损失（公式10）按Token总数加权，迫使模型为每个Token负责，避免“用废话凑长度”，熵值反映真实有效多样性。 总体看，基线模型像话痨学生，为凑字数说废话（熵值暴增），老师（损失函数）却按篇给分，导致废话连篇。DAPO像“逻辑老师”，每句话（Token）单独打分，学生被迫说有意义的话，熵值虽低但句句关键。

传统GRPO按样本平均损失（Sample-level），导致长序列的每个Token贡献被稀释（如1000Token的样本和100Token的样本权重相同）。 DAPO改用Token级加权（分母为总Token数），使长序列的有效Token获得更高梯度权重，鼓励模型生成“有意义的长推理”而非“无意义的长废话”。

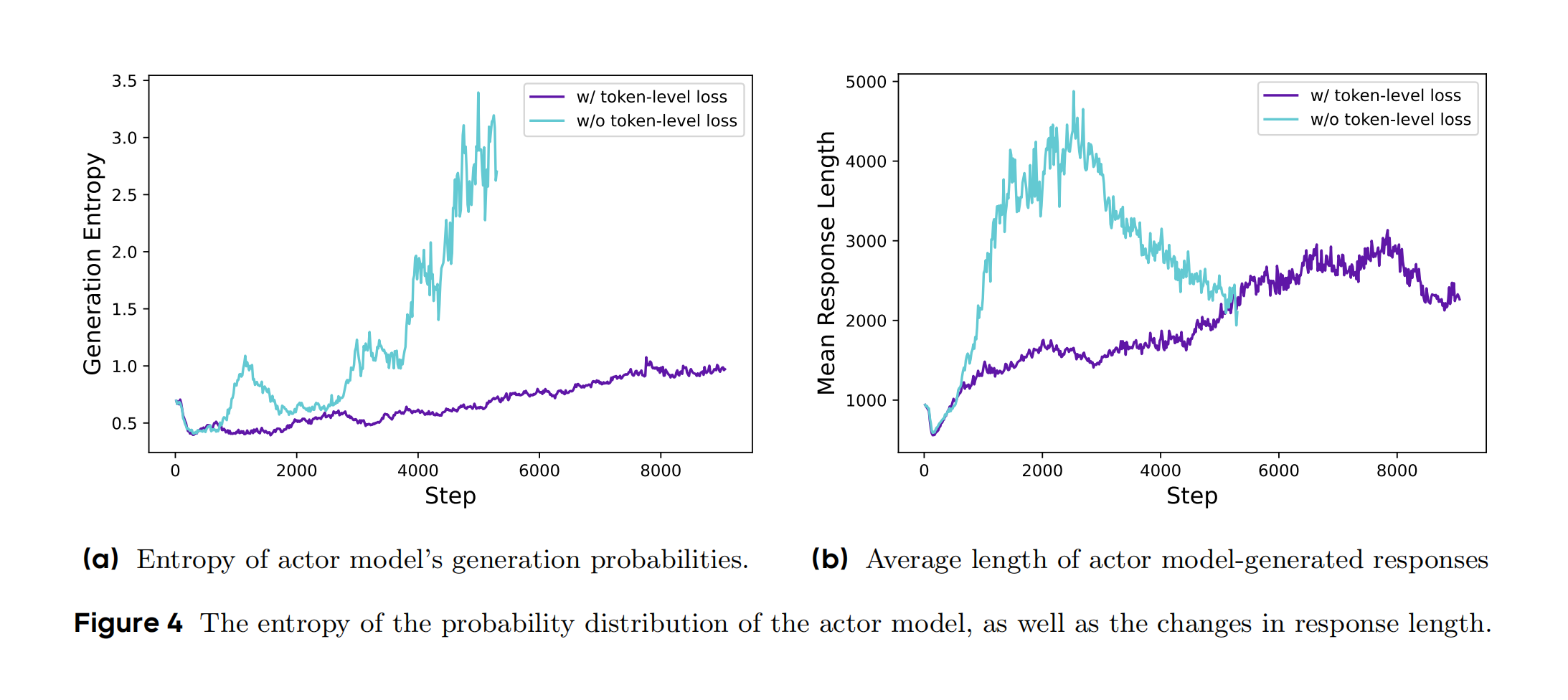
绿色曲线（w/o token-level loss）表示未应用时的基线模型，紫色曲线（w/ token-level loss）应用动态采样策略后的训练进展。

Figure 4 包含 两个子图，展示 Token级策略梯度损失 对训练过程的影响：

• 子图(a)：生成熵（Entropy）对比

  • 绿色曲线（w/o Token-level loss）： 熵值从0.5快速增长，5000步时骤升至3.0，后面未继续绘制，可能是随后因无效生成过多导致曲线截断。样本级损失导致长序列的无效Token被平均化，模型为追求奖励盲目生成高熵（多样性）内容，但包含大量无意义重复或错误推理。

  • 紫色曲线（w/ Token-level loss）： 熵值从0.5缓慢增加，9000步时稳定在1.0左右，曲线平滑无剧烈波动。Token级损失按每个Token贡献加权梯度，抑制低质量高熵生成，保留有效推理的多样性（如多步验证、公式推导等有意义的变化）。

• 子图(b)：平均响应长度（Mean Response Length）对比

  • 绿色曲线（w/o Token-level loss）：从1000 tokens快速增长，5000步时突破3000 tokens，后续因生成大量无效内容（如重复计算步骤、无意义符号）导致曲线失控，最终截断。样本级损失无法区分有效/无效Token，模型通过堆砌内容提升奖励，形成“长度膨胀但推理无效”的恶性循环。

  • 紫色曲线（w/ Token-level loss）：DAPO模型响应长度。从1000 tokens缓慢增加，9000步时稳定在1800 tokens，曲线平滑且无骤增。Token级损失对有效推理步骤（如公式推导、逻辑转折）赋予更高梯度权重，鼓励模型生成“紧凑且逻辑完整”的长序列，避免无意义扩张。 结合两个子图看，基线模型的长度膨胀是“注水”，DAPO的长度增长是“精炼”，每增加100 tokens对应1-2步有效推理。

3.4 ✨ 改进4：超长奖励塑形（控制答案长度）

超出长度的部分逐步扣分（类似考试作文字数限制），通过长度感知惩罚缓解截断样本的奖励噪声。DAPO的分段惩罚设计（论文公式13）：
$$R_{\text{length}}(y)=\{\begin{array}{ll}0,& |y|\le L_{\text{max}}-L_{\text{cache}}\text{（安全区：不惩罚）}\\ \frac{(L_{\text{max}}-L_{\text{cache}})-|y|}{L_{\text{cache}}},& L_{\text{max}}-L_{\text{cache}}<|y|\le L_{\text{max}}\text{（缓冲区：线性惩罚）}\\ -1,& |y|>L_{\text{max}}\text{（超长篇：强惩罚）}\end{array}$$

• 安全区（如 0 - 4096 tokens）：允许模型生成较长但合理的推理序列（如10步以上推导），不施加惩罚。
• 缓冲区（4096 - 20480 tokens）：随长度增加渐进惩罚，避免突然降分，给模型调整空间。
• 超长篇（ > 20480 tokens）：强惩罚抑制无意义超长生成（如重复、乱码）。

通俗的比喻，考试改革了：只训练中等难度题目（动态采样）。允许偏科学生在弱项进步更多（解耦剪裁）。作文每句话都算分（Token级损失）。字数超限逐步扣分（超长奖励塑形）。

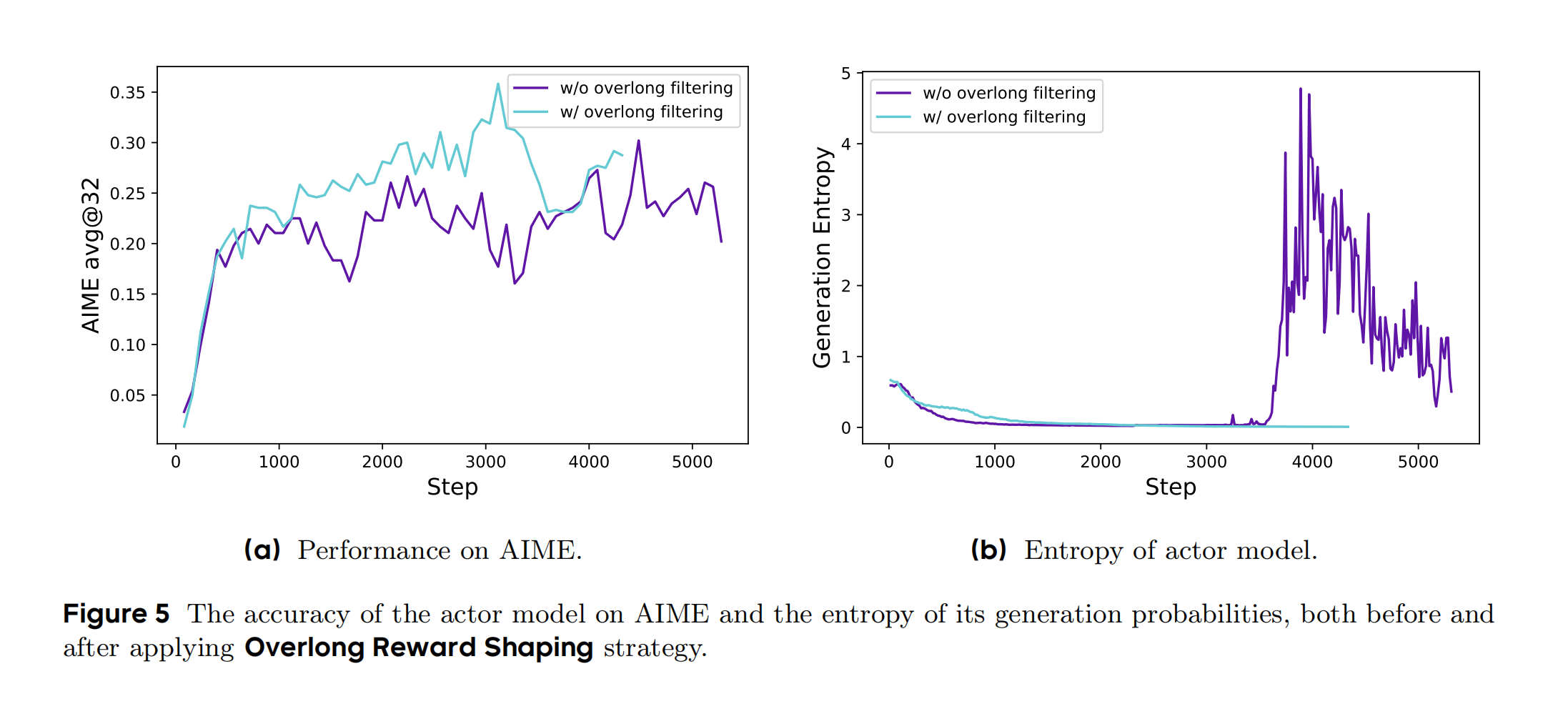
紫色曲线（w/o overlong filtering）表示未应用时的基线模型，绿色曲线（w/ overlong filtering）应用动态采样策略后的训练进展。 注意，这里曲线的颜色换了，之前的多幅图都是 绿色曲线是基线。

Figure 5 展示了 DAPO 中 超长奖励塑形（Overlong Reward Shaping） 策略对训练过程的影响，包含两个子图：

• 子图(a)：AIME测试集准确率对比

  • 紫色曲线（w/o Overlong Filtering）：准确率整体低于绿色曲线，最大值出现在3500步的0.3。传统“一刀切”惩罚（如直接赋-1）误罚合理长推理序列，导致模型难以区分“长度过长”与“推理错误”，梯度更新受噪声干扰。
  • 绿色曲线（w/ Overlong Filtering）：准确率整体高于基线，最大值出现在3000步的0.35。通过“软超长惩罚”（Soft Overlong Punishment）区分长度范围，允许模型在合理长度内探索复杂推理，抑制无意义超长生成，减少奖励噪声对训练的干扰。

• 子图(b)：生成熵（Entropy）对比

  • 紫色曲线（w/o Overlong Filtering）：熵值在3500步之前稳定下降，之后熵值突增。
  • 绿色曲线（w/ Overlong Filtering）：熵值稳定下降，未出现波动或则突增的。

公式图解对比：

PPO目标：
min(新旧策略比×绝对优势, 截断后的新旧策略比×绝对优势)

GRPO目标：
min(新旧策略比×相对优势, 截断后的新旧策略比×相对优势) － KL惩罚项

DAPO目标：
min(新旧策略比×动态采样后的相对优势, 解耦剪裁后的新旧策略比×相对优势) 
+ Token级权重调整 
+ 超长惩罚项

适用场景指南：

算法	推荐场景	不推荐场景
PPO	老师打分，简单任务（如游戏控制）	稀疏奖励、大模型显存受限
GRPO	班级排名，数学推理、代码生成	连续控制任务
DAPO	精准打击，复杂长文本推理（如AIME竞赛）	小模型轻量级训练

4. 实验与结果

4.1 主要结果

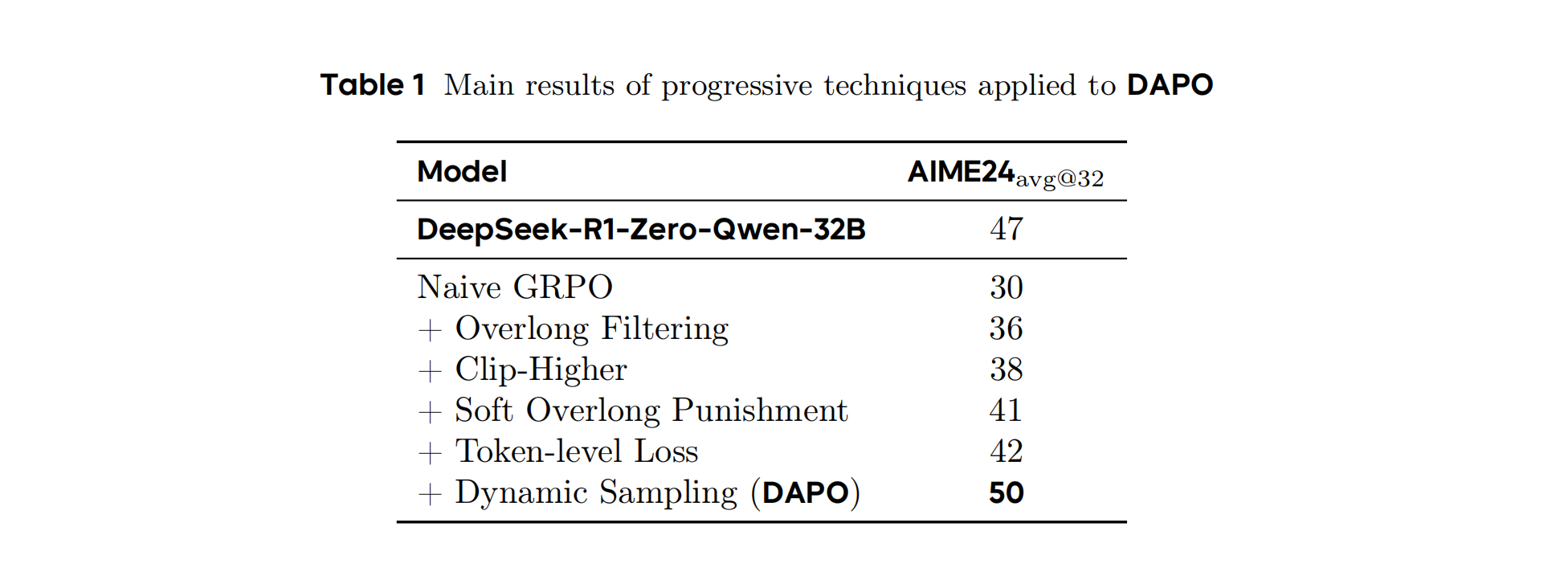
Table 1 展示了核心技术组件的消融实验结果，量化了各创新点对 AIME 2024 准确率的贡献。

4.2 训练动态分析

• 响应长度：稳定增长至约4000 tokens（Figure 7a），反映推理复杂度提升。
• 奖励分数：训练集奖励持续上升，但需警惕过拟合（Figure 7b）。
• 熵值与概率：通过Clip-Higher维持合理熵值（Figure 7c），避免概率分布坍塌（Figure 7d）。

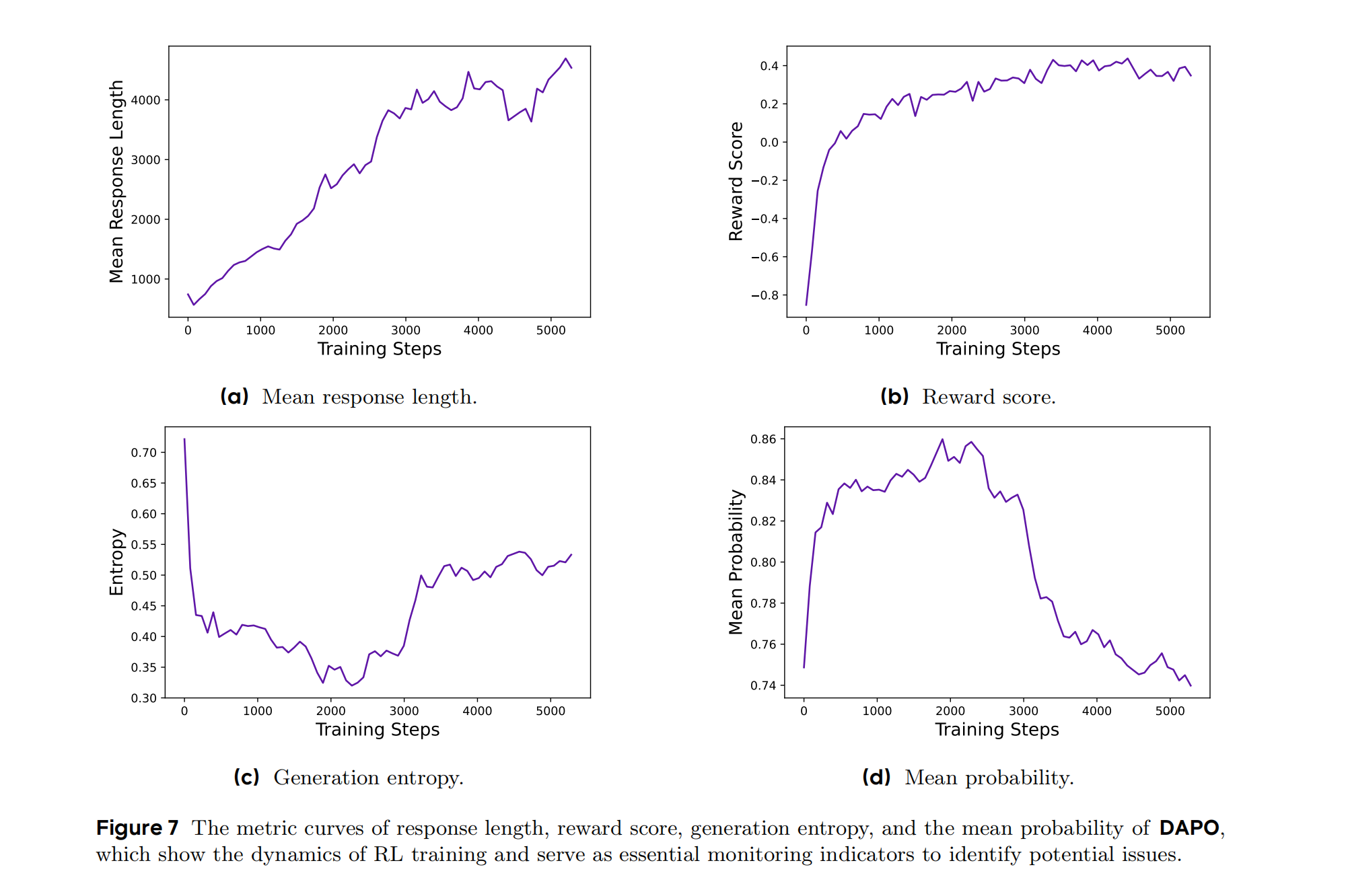
Figure 7 展示了 DAPO 训练过程中的四个关键指标随训练步数的变化趋势，横坐标为训练步数（0-5000步），纵坐标分别为：

• 子图(a)：平均响应长度（Mean Response Length）： 曲线从约2000 tokens 逐步增长至4000 tokens，最终稳定在约3500 tokens。 响应长度增长表明模型生成更复杂的推理步骤（如多步验证、反思行为），但未出现无意义的超长生成（如基线模型可能的熵坍塌导致的冗长输出）。
• 子图(b)：奖励分数（Reward Score）：曲线（奖励分数）在训练初期快速上升至0.2，随后略有波动但保持稳定。 奖励分数反映模型在训练集上的表现，稳定的高分表明模型有效拟合了训练数据，但需警惕过拟合（测试集准确率可能低于训练集）。
• 子图©：生成熵（Entropy）：曲线（熵值）在训练初期从0.7下降到0.4，中期回升至0.5，最终稳定。 熵值代表输出多样性。DAPO通过Clip-Higher策略保持较高熵值，避免输出趋同，同时抑制低质量的过度探索（如基线模型可能的熵坍塌）。
• 子图(d)：平均概率（Mean Probability）： 曲线（平均概率）从0.74逐步上升至0.86，最终下降到0.74。 平均概率增长表明模型对正确输出的置信度提升，但未因过拟合导致概率分布过于陡峭（如基线模型可能的高概率坍塌）。

通俗理解：

• 子图(a)：模型越来越擅长“写长作文”，但不会乱写。
• 子图(b)：老师给的“训练分数”很高，但考试（测试集）成绩可能略低。
• 子图©：学生保持“脑洞大开”，但不过度放飞自我。
• 子图(d)：学生对正确答案越来越自信，但不会“钻牛角尖”。

4.3 案例研究

在强化学习训练过程中，我们观察到一个有趣的现象：参与者模型的推理模式会随着时间的推移而动态演变。具体来说，该算法不仅强化了有助于正确解决问题的现有推理模式，而且还逐渐产生了最初不存在的全新推理模式。这一发现揭示了强化学习算法的适应性和探索能力，并为模型的学习机制提供了新的见解。例如，在模型训练的早期阶段，几乎没有发生检查和反思先前的推理步骤的情况。然而，随着训练的进行，模型表现出不同的反思和回溯行为，如 Table 2 所示。

Table 2 展示了训练过程中模型推理行为的进化，特别是**反思行为（Reflective Behavior）**的涌现——模型从“直接推导”进化到“自我检查与修正”。

Question（几何推理题）：

给定四面体 $S-ABC$ 的底面 $ABC$ 为等边三角形，点 $A$ 在面 $SBC$ 上的投影 $H$ 是 $△SBC$ 的垂心，二面角 $H-AB-C$ 为 $30^{\circ }$ ，且 $SA=2$ ，求四面体的体积（答案形式为分数 $\frac{k}{m}$ ，需计算 $k+m$ ）。 问题核心需综合利用垂心、二面角、边长等几何条件，涉及空间坐标设定、向量正交关系和体积计算，属于复杂多步推理任务。

Response（模型响应对比）：

训练阶段	模型响应片段	核心差异
早期	“设点 $S$ 的坐标为 $(x,y,z)$ ，由 $SA=2$ 得 $x^2+y^2+z^2=4$ 。 由于 $H$ 是 $△SBC$ 的垂心，故 $SB=SC$ ，推测 $△SBC$ 为等边三角形，进而计算高和体积为 $\frac{\sqrt{3}}{3}$ 。”	无反思行为： 1. 直接假设 $△SBC$ 为等边三角形（未验证垂心性质）； 2. 线性推导，未检查中间步骤的几何关系（如二面角条件未充分利用）。
后期	“设 $S$ 的坐标为 $(x,y,z)$ ，由 $SA=2$ 得 $x^2+y^2+z^2=4$ 。 但注意到 $H$ 是垂心，需满足 $SB\perp HC$ 且 $SC\perp HB$，这表明 $S$ 的坐标需满足正交条件 $(x-x_H)(x_C-x_H)+(y-y_H)(y_C-y_H)=0$ （修正前期假设）。 结合二面角 $30^{\circ }$ 重新计算高，最终体积为 $\frac{1}{2}$ ，故 $k+m=1+2=3$ 。”	反思行为涌现： 1. 主动识别前期假设错误（垂心不必然导致等边三角形）； 2. 插入正交条件验证（ $SB\perp HC$ ），修正推理路径； 3. 充分利用所有几何条件（二面角、垂心性质），避免错误推导。

5. 结论与未来方向

5.1 贡献总结

DAPO通过四大创新技术（Clip-Higher、动态采样、Token级损失、超长奖励塑形），在AIME 2024基准上实现50分的开源最优成绩，训练效率提升50%。其开源系统为行业提供了可复现的大规模RL解决方案。

5.2 未来方向

1. 数据增强：结合树搜索解码策略提升样本多样性。
2. 算法鲁棒性：开发抗噪声奖励模型（如Weak-to-Strong方法）。
3. 多模态扩展：探索DAPO在代码生成、定理证明等领域的应用。