K-Means++

不同于K-Means算法第一次是随机选择K个聚类中心，K-Means++是假设已经选取了𝑝个初始聚类中心(0<𝑝<𝐾)，则在选取第𝑝+1个聚类中心时：距离当前𝑝个聚类中心越远的点会有更高的概率被选为第𝑝+1个聚类中心。只有在选取第一个聚类中心(𝑝=1)时是通过随机的方法。该改进方法符合一般的直觉：聚类中心互相之间距离得越远越好。这个改进直观简单，也非常有效。

K-Mediods

K-Mediods是基于原型的另一种聚类算法，也是对K-Means算法的一种改进。

算法描述:

1. 随机选取一组样本作为中心点集；
2. 每个中心点对应一个簇；
3. 计算各样本点到各个中心点的距离（如欧氏距离），将样本点放入距离中心点最短的那个簇中；
4. 计算各簇中，距簇内各样本点距离的绝对误差最小的点，作为新的中心点；
5. 如果新的中心点集与原中心点集相同，算法终止；如果新的中心点集与原中心点集不完全相同，返回2)。

K-Mediods聚类算法原理和K-Means大体相似，算法流程基本一致，不同的是:

• 质心的计算方式不同

K-Means聚类算法更新聚簇中心的时候直接计算均值，以均值点作为新的中心，可能是样本点中不存在的点；而K-Mediods更新聚簇中心是计算每一个点到簇内其他点的距离之和，选择距离和最小的点来作为新的聚簇中心，质心必须是某些样本点的值。

• K-Mediods可以避免数据中的异常值带来的影响。

如一个二维的样本集划分的簇是{(1，1)，(1，2)，(2，1)，(1000，1000)}，其中(1000，1000)是噪声点。按照K-Means算法，该样本集的质心则为(502，502)，但这个新的质心并不是该样本集大多数正常样本点围绕的中心；如果是选择K-Medoids就可以避免这种情况，它会在{(1，1)，(1，2)，(2，1)，(1000，1000)}中选出一个样本点使它到其他所有点的距离之和绝对误差最小，计算可知一定会在前三个点中选取。

层次聚类

层次聚类法试图在不同层次对数据集进行划分，从而形成树形的聚类结构，数据集的划分可采用“自下向上”的聚合策略，也可以采用“自顶向下”的分拆策略。聚类的层次被表示成树形图。树根拥有所有样本的唯一聚类，叶子是仅有一个样本的聚类。

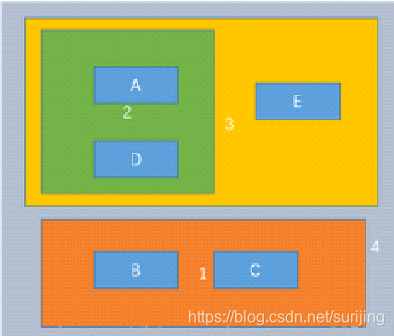
其中将A、B、C、D、E五个对象进行层级聚类，最终的聚类步骤上面已经标出（1，2，3，4）。 循环遍历所有对象，利用算法计算对象点之间的距离，每次将最近的两个对象聚为一类，直到得到最终的结果。
衡量簇之间的距离方法

单链接（最小距离）	定义簇的邻近度为不同两个簇的两个最近的点之间的距离，容易受极端值的影响，两个不相似的点可能由于其中的某个极端点 距离较近而组合在一起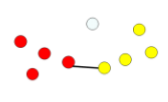
全连接（最大距离）	定义簇的邻近度不同两个簇的两个最远点之间的距离 ，两个相似的点可能某个点原先所在的簇中有极端值而无法组合在一起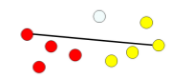
均连接（平均）	定义簇的邻近度为取自两个不同簇的所有点对邻近度的平均值。计算两个簇中的每个点与其他所有点的距离并将所有距离的均值作为两个组合数 据点间的距离，此方法计算量比较大，但结果比前两种方法更合理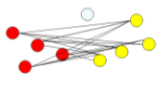
ward(方差)	所有聚类内的平方差总和。 最小化所有聚类内的平方差总和。ESS

基本思路：

• 将每个对象作为一个簇𝑐_𝑖={𝑥_𝑖}，形成簇的集合 𝐶={𝑐_𝑖}；

• 迭代以下步骤直至所有对象都在一个族中；

• 找到一对距离最近的簇：min 𝐷"(" 𝑐_𝑖，𝑐_𝑗 “)”；

• 将这对簇合并为一个新的簇；

• 从原集合C中移除这对簇；

• 最终产生层次树形的聚类结构: 树形图。
  优点：

• 可排除噪声点的干扰，但有可能噪声点分为一簇。

• 适合形状不规则，不要求聚类完全的情况

• 不必确定𝐾值，可根据聚类程度不同有不同的结果。

• 原理简单，易于理解。
  缺点：

• 计算量很大，耗费的存储空间相对于其他几种方法要高。

• 合并操作不能撤销。

• 合并操作必须有一个合并限制比例，否则可能发生过度合并导致所有分类中心聚集，造成聚类失败。

BIRCH算法

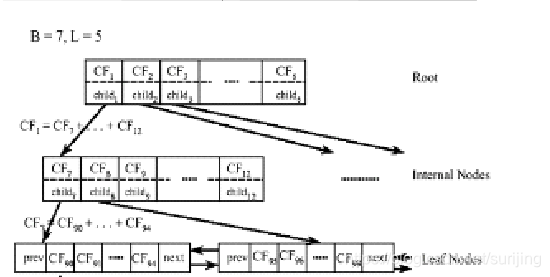
BIRCH算法即平衡迭代削减聚类法，其核心是用一个聚类特征3元组表示一个簇的有关信息，从而使一簇点的表示可用对应的聚类特征，而不必用具体的一组点来表示。它通过构造满足分支因子和簇直径限制的聚类特征树来求聚类。

• 3元组包含：数据点个数，数据点特征之和，数据点特征的平方和
• 分支因子：规定了树的每个节点的样本个数
• 簇直径：体现一类点的距离范围

1.BIRCH算法通过聚类特征可以方便地进行中心、半径、直径及类内、类间距离的运算。
2.BIRCH算法中聚类特征树的构建过程是动态的，可以随时根据新的数据点对树进行重构，适合大规模数据集。

DBSCAN

存在数据集𝐷={𝑥_1,𝑥_2,…,𝑥_𝑚 }，DBSCAN的相关密度概念描述如下：

• 𝛆−邻域：对于𝑥_𝑗∈𝐷，其𝜀−邻域包含样本集𝐷中与𝑥_𝑗 的距离不大于𝜀的点构成一个子样本集，即𝑁_𝜀
  (𝑥_𝑗)={𝑥_𝑗∈𝐷|𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑒(𝑥_𝑖
  〖,𝑥〗_𝑗)≤𝜀}，该子样本集的样本个数记为|𝑁_𝜀 (𝑥_𝑗)|。
• 核心对象：对于任一样本𝑥_𝑗∈𝐷，如果其𝜀−邻域对应的𝑁_𝜀 (𝑥_𝑗
  )至少包含min⁡_𝑠𝑎𝑚𝑝𝑙𝑒𝑠个样本，即如果|𝑁_𝜀
  (𝑥_𝑗)|≥min⁡_𝑠𝑎𝑚𝑝𝑙𝑒𝑠，则𝑥_𝑗是核心对象。
• 密度直达：如果𝑥_𝑖位于𝑥_𝑗 的𝜀−"邻域"
  中，且𝑥_𝑗是核心对象，则称𝑥_𝑖由𝑥_𝑗密度直达。注意反之不一定成立，即不能说𝑥_𝑗由𝑥_𝑖密度直达，除非且𝑥_𝑖也是核心对象。
• 密度可达：对𝑥_𝑖 和𝑥_𝑗，如果存在样本序列𝑝_1, 𝑝_2,…,
  𝑝_𝑇，满足𝑝_1=𝑥_𝑖，𝑝_𝑇=𝑥_𝑗，且𝑝_(𝑡+1)
  由𝑝_𝑡密度直达，则称𝑥_𝑗由𝑥_𝑖密度可达，密度可达满足传递性。此时𝑝_1, 𝑝_2,…,
  𝑝_(𝑇−1)均为核心对象，因为只有核心对象才能使其他样本密度直达。另外，密度可达不满足对称性，由密度直达的不对称得出。
• 密度相连：对于𝑥_𝑖 和𝑥_𝑗，如果存在核心对象样本𝑥_𝑘，使𝑥_𝑖 和𝑥_𝑗均由𝑥_𝑘密度可达，则称𝑥_𝑖
  和𝑥_𝑗密度相连。注意密度相连关系是满足对称性的。

DBSCAN算法将数据点分为三类：

• 核心点：在半径𝜀内含有超过min⁡_𝑠𝑎𝑚𝑝𝑙𝑒𝑠数目的点。

• 边界点：在半径𝜀内点的数量小于min⁡_𝑠𝑎𝑚𝑝𝑙𝑒𝑠，但是落在核心点的邻域内的点

• 噪音点：既不是核心点也不是边界点的点。
  过程
  1.将所有点标记为核心点、边界点或噪声点；
  2.删除噪声点；
  3.为距离在Eps之内的所有核心点之间赋予一条边；
  4.每组连通的核心点形成一个簇； 5.将每个边界点指派到一个与之关联的核心点的簇中（哪一个核心点的半径范围之内）。

DBSCAN的优点：

• 可以解决数据分布特殊（非凸， 互相包络，长条形等）的情况。

• 对于噪声不敏感 ，速度较快，不需要指定簇的个数；

• 可适用于较大的数据集。

• 在邻域参数给定的情况下结果是确定的，只要数据进入算法的顺序不变，与初始值无关。

缺点：

• 因为对整个数据集我们使用的是一组邻域参数 ，簇之间密度差距过大时效果不好。

• 数据集较大的时候很消耗内存。

• 对于高维数据距离的计算会比较麻烦，造成维数灾难。