【ML】第18章 强化学习
强化学习(RL)是当今机器学习最令人兴奋的领域之一,也是最古老的领域之一。它自 1950 年代就已存在,多年来产生了许多有趣的应用程序,特别是在游戏(例如,TD-Gammon,一种双陆棋游戏程序)和机器控制方面,但很少成为头条新闻。但是在 2013 年发生了一场革命,当时来自一家名为 DeepMind 的英国初创公司的研究人员,最终在大多数游戏中,仅使用原始像素作为输入,而无需任何有关游戏规则的先
🔎大家好,我是Sonhhxg_柒,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流🔎
📝个人主页-Sonhhxg_柒的博客_CSDN博客 📃
🎁欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏 - 机器学习【ML】 自然语言处理【NLP】 深度学习【DL】
🖍foreword
✔说明⇢本人讲解主要包括Python、机器学习(ML)、深度学习(DL)、自然语言处理(NLP)等内容。
如果你对这个系列感兴趣的话,可以关注订阅哟👋
强化学习(RL)是当今机器学习最令人兴奋的领域之一,也是最古老的领域之一。它自 1950 年代就已存在,多年来产生了许多有趣的应用程序,1特别是在游戏(例如,TD-Gammon,一种双陆棋游戏程序)和机器控制方面,但很少成为头条新闻。但是在 2013 年发生了一场革命,当时来自一家名为 DeepMind 的英国初创公司的研究人员展示了一个系统,该系统可以从头开始学习玩几乎任何 Atari 游戏,2最终在大多数游戏中胜过人类3 ,仅使用原始像素作为输入,而无需任何有关游戏规则的先验知识。4这是一系列令人惊叹的壮举中的第一个,最终在 2016 年 3 月,他们的系统 AlphaGo 战胜了围棋传奇职业选手李世石,并在 2017 年 5 月战胜了世界冠军柯洁。从来没有一个程序能接近击败这个游戏的高手,更不用说世界冠军了。今天,RL 的整个领域都在沸腾着新的想法,有着广泛的应用。DeepMind 在 2014 年被谷歌以超过 5 亿美元的价格收购。
那么 DeepMind 是如何实现这一切的呢?事后看来,这似乎很简单:他们将深度学习的力量应用于强化学习领域,并且超出了他们最疯狂的梦想。在本章中,我们将首先解释强化学习是什么以及它擅长什么,然后介绍深度强化学习中最重要的两种技术:策略梯度和深度 Q 网络(DQN),包括对马尔可夫决策过程的讨论(MDP)。我们将使用这些技术来训练模型以平衡移动推车上的杆子;然后我将介绍 TF-Agents 库,它使用最先进的算法,大大简化了构建强大的 RL 系统的过程,我们将使用该库来训练代理来玩著名的 Atari 游戏Breakout。我将通过看看该领域的一些最新进展来结束本章。
学习优化奖励
在强化学习,软件代理在环境中进行观察并采取行动,作为回报,它会获得奖励。它的目标是学习以一种随着时间的推移最大化其预期回报的方式行事。如果您不介意一点拟人化,您可以将正面奖励视为快乐,将负面奖励视为痛苦(在这种情况下,“奖励”一词有点误导)。简而言之,智能体在环境中行动并通过反复试验来学习,以最大限度地提高其乐趣并最大限度地减少其痛苦。
这是一个相当广泛的设置,可以应用于各种各样的任务。下面是几个例子(见图 18-1):
-
代理可以是控制机器人的程序。在这种情况下,环境就是现实世界,代理通过一组传感器(如摄像头和触摸传感器)观察环境,其动作包括发送信号以激活电机。它可以被编程为在接近目标目的地时获得正奖励,而在浪费时间或走错方向时获得负奖励。
-
代理可以是控制吃豆人小姐的程序。在这种情况下,环境是 Atari 游戏的模拟,动作是九个可能的操纵杆位置(左上、下、中心等),观察结果是屏幕截图,奖励只是游戏点数。
-
类似地,代理可以是玩围棋等棋盘游戏的程序。
-
代理不必控制物理(或虚拟)移动的东西。例如,它可以是一个智能恒温器,当它接近目标温度并节省能源时,它会获得积极的回报,而当人类需要调整温度时,它会获得消极的回报,因此智能体必须学会预测人类的需求。
-
代理可以观察股票市场价格并决定每秒买入或卖出多少。奖励显然是金钱上的收益和损失。

图 18-1。强化学习示例:(a) 机器人,(b)吃豆人女士,(c) 围棋玩家,(d) 恒温器,(e) 自动交易者5
请注意,可能根本没有任何积极的奖励;例如,代理可能在迷宫中四处走动,在每个时间步都得到负奖励,所以它最好尽快找到出口!还有许多其他强化学习非常适合的任务示例,例如自动驾驶汽车、推荐系统、在网页上放置广告或控制图像分类系统应将注意力集中在哪里。
政策搜索
这软件代理用来确定其动作的算法是称其为政策。该策略可以是一个将观察结果作为输入并输出要采取的动作的神经网络(见图 18-2)。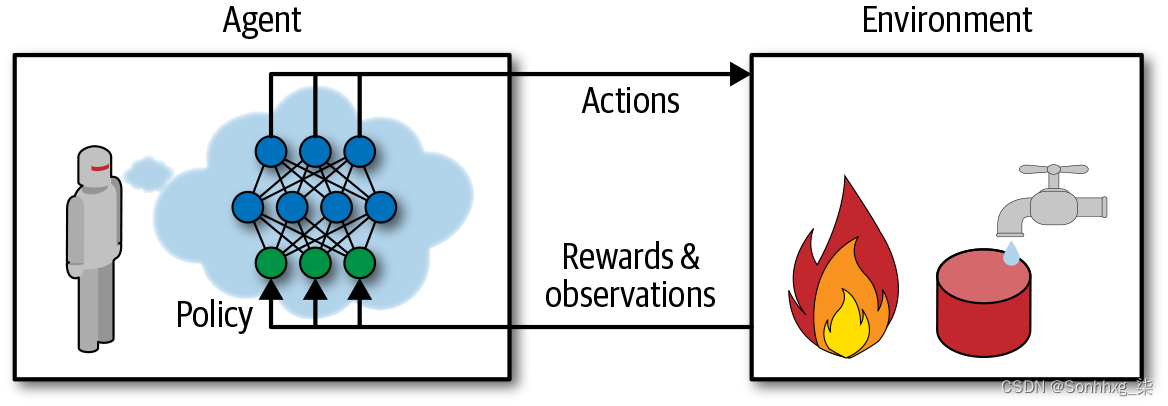
图 18-2。使用神经网络策略的强化学习
该策略可以是您能想到的任何算法,并且不必是确定性的。事实上,在某些情况下它甚至不必观察环境!例如,考虑一个机器人真空吸尘器,其奖励是它在 30 分钟内拾取的灰尘量。它的策略可以是每秒以某个概率p向前移动,或者以概率 1 – p随机向左或向右旋转。旋转角度将是介于 – r和 + r之间的随机角度。自从该策略涉及一些随机性,称为随机策略。机器人将有一个不稳定的轨迹,这保证了它最终会到达它可以到达的任何地方并捡起所有的灰尘。问题是,它会在 30 分钟内吸走多少灰尘?
你会如何训练这样的机器人?那里只是您可以调整的两个策略参数:概率p和角度范围r。一种可能的学习算法是为这些参数尝试许多不同的值,然后选择性能最佳的组合(见图 18-3)。这是策略搜索的一个示例,在这种情况下使用蛮力方法。什么时候策略空间太大(通常是这种情况),以这种方式找到一组好的参数就像大海捞针一样。
其他探索策略空间的方法是使用遗传算法。例如,您可以随机创建 100 个策略的第一代并尝试它们,然后“杀死” 80 个最差策略6并使 20 个幸存者每人产生 4 个后代。后代是其父7的副本加上一些随机变化。幸存的政策及其后代共同构成第二代。您可以通过这种方式继续迭代几代,直到找到一个好的策略。8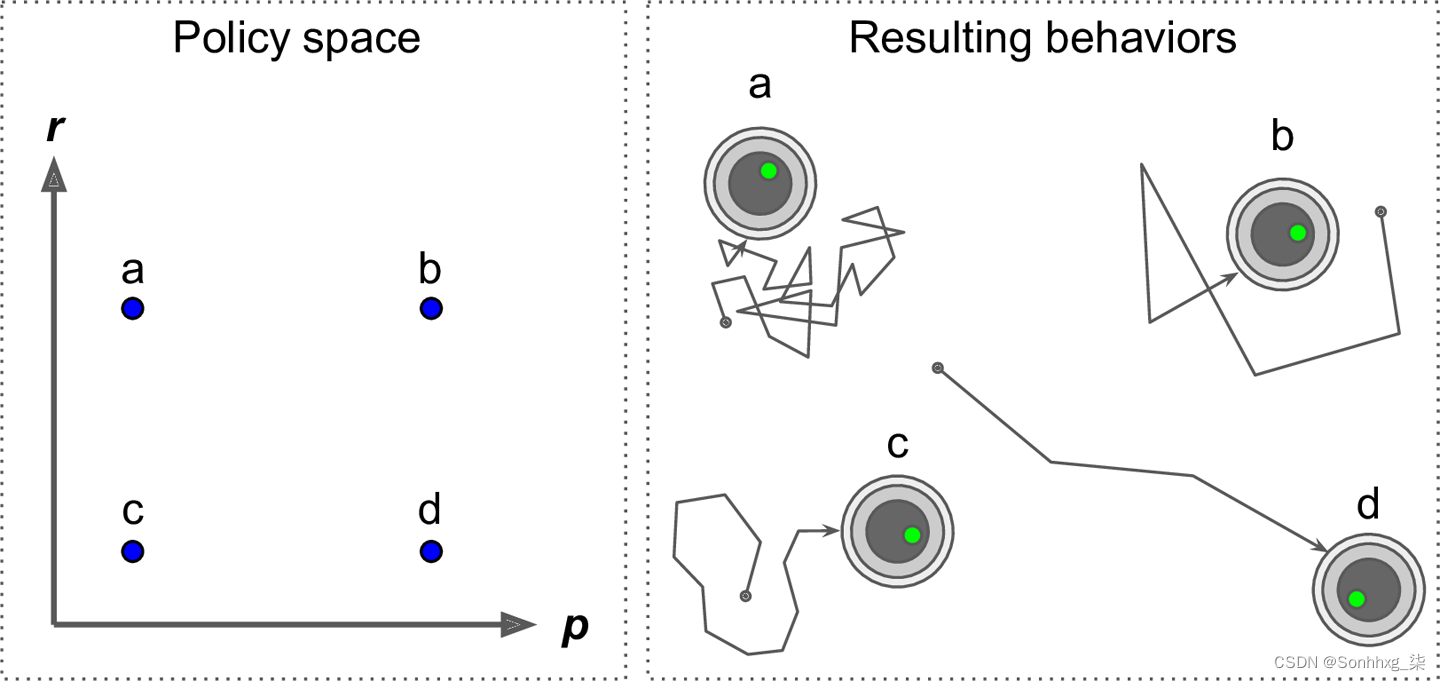
图 18-3。策略空间中的四个点(左)和代理的相应行为(右)
另一种方法是使用优化技术,通过评估与策略参数相关的奖励梯度,然后通过遵循梯度向更高奖励调整这些参数。9我们将讨论这个方法称为策略梯度(PG),本章稍后将详细介绍。回到真空吸尘器机器人,您可以稍微增加p并评估这样做是否会增加机器人在 30 分钟内拾取的灰尘量;如果是,则增加p一些,否则减少p。我们将使用 TensorFlow 实现一个流行的 PG 算法,但在此之前,我们需要为代理创建一个居住环境——所以是时候介绍 OpenAI Gym。
OpenAI Gym 简介
一强化学习的挑战之一是,为了训练代理,首先需要有一个工作环境。如果您想编写一个学习玩 Atari 游戏的代理程序,您将需要一个 Atari 游戏模拟器。如果你想给一个行走的机器人编程,那么环境就是现实世界,你可以直接在那个环境中训练你的机器人,但这有它的局限性:如果机器人从悬崖上掉下来,你不能只点击撤消。你也不能加快时间;增加更多的计算能力不会使机器人移动得更快。而且并行训练 1000 个机器人的成本通常太高。简而言之,在现实世界中训练既难又慢,所以您通常至少需要一个模拟环境来进行引导训练。例如,您可以使用PyBullet或MuJoCo 之类的库进行 3D 物理模拟。
OpenAI Gym 10是一个提供各种模拟环境(Atari 游戏、棋盘游戏、2D 和 3D 物理模拟等)的工具包,因此您可以训练代理、比较它们或开发新的 RL 算法。
在安装工具包之前,如果你使用 virtualenv 创建了一个隔离环境,你首先需要激活它:
$ cd $ML_PATH # Your ML working directory (e.g., $HOME/ml)
$ source my_env/bin/activate # on Linux or macOS
$ .\my_env\Scripts\activate # on Windows接下来,安装 OpenAI Gym(如果您不使用虚拟环境,则需要添加--user选项,或者具有管理员权限):
$ python3 -m pip install -U gym根据您的系统,您可能还需要安装 Mesa OpenGL Utility (GLU) 库(例如,在 Ubuntu 18.04 上您需要运行apt install libglu1-mesa)。需要这个库来渲染第一个环境。接下来,打开 Python shell 或 Jupyter notebook 并使用以下命令创建环境make():
>>> import gym
>>> env = gym.make("CartPole-v1")
>>> obs = env.reset()
>>> obs
array([-0.01258566, -0.00156614, 0.04207708, -0.00180545])在这里,我们创建了一个 CartPole 环境。这是一个 2D 模拟,其中可以向左或向右加速小车,以平衡放置在其顶部的杆(见图 18-4)。您可以通过运行获取所有可用环境的列表gym.envs.registry.all()。创建环境后,您必须使用该reset()方法对其进行初始化。这将返回第一个观察结果。观察取决于环境的类型。对于 CartPole 环境,每个观测值都是一个包含四个浮点数的 1D NumPy 数组:这些浮点数表示小车的水平位置(0.0= 中心)、它的速度(正表示右)、极点的角度(0.0= 垂直)和它的角速度(正表示顺时针)。
现在让我们通过调用它的render()方法来显示这个环境(见图18-4)。在 Windows 上,这需要首先安装 X 服务器,例如 VcXsrv 或 Xming:
>>> env.render()
True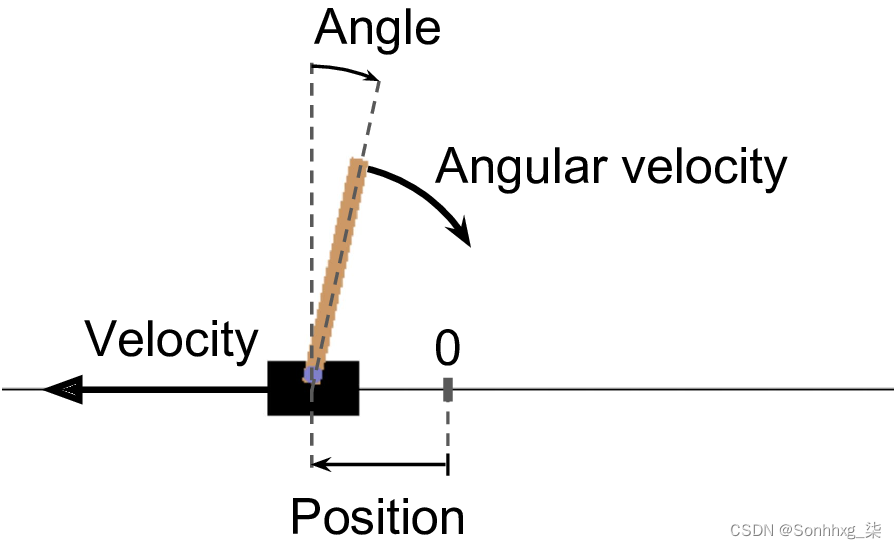
图 18-4。CartPole 环境
小费
如果您使用的是无头服务器(即没有屏幕),例如云上的虚拟机,渲染将失败。避免这种情况的唯一方法是使用伪造的 X 服务器,例如 Xvfb 或 Xdummy。例如,您可以安装 Xvfb(
apt install xvfb在 Ubuntu 或 Debian 上)并使用以下命令启动 Pythonxvfb-run -s "-screen 0 1400x900x24" python3:. 或者,安装 Xvfb 和pyvirtualdisplay库(包装 Xvfb)并pyvirtualdisplay.Display(visible=0, size=(1400, 900)).start()在程序的开头运行。
如果您想render()将渲染图像作为 NumPy 数组返回,您可以设置mode="rgb_array"(奇怪的是,此环境也会将环境渲染到屏幕上):
>>> img = env.render(mode="rgb_array")
>>> img.shape # height, width, channels (3 = Red, Green, Blue)
(800, 1200, 3)让我们询问环境可以执行哪些操作:
>>> env.action_space
Discrete(2)Discrete(2)表示可能的动作是整数 0 和 1,分别代表向左 (0) 或向右 (1) 加速。其他环境可能具有额外的离散动作或其他类型的动作(例如,连续的)。由于杆向右倾斜 ( obs[2] > 0),让我们将推车向右加速:
>>> action = 1 # accelerate right
>>> obs, reward, done, info = env.step(action)
>>> obs
array([-0.01261699, 0.19292789, 0.04204097, -0.28092127])
>>> reward
1.0
>>> done
False
>>> info
{}该step()方法执行给定的操作并返回四个值:
obs
这是新的观察。购物车现在向右移动 ( obs[1] > 0)。杆子仍然向右倾斜(obs[2] > 0),但它的角速度现在是负的(obs[3] < 0),所以在下一步之后它很可能会向左倾斜。
reward
在这种环境下,无论您做什么,每一步都会获得 1.0 的奖励,因此目标是尽可能长时间地保持情节运行。
done
该值将是True剧集结束时的值。当杆子倾斜太多,或者离开屏幕,或者在 200 步之后(在最后一种情况下,你赢了),就会发生这种情况。之后,必须重置环境才能再次使用。
info
这个特定于环境的字典可以提供一些额外的信息,您可能会发现这些信息对调试或培训很有用。例如,在某些游戏中,它可能指示代理有多少生命。
小费
一旦你使用完一个环境,你应该调用它的
close()方法来释放资源。
让我们硬编码一个简单的策略,当杆向左倾斜时向左加速,当杆向右倾斜时向右加速。我们将运行此策略以查看超过 500 集的平均奖励:
def basic_policy(obs):
angle = obs[2]
return 0 if angle < 0 else 1
totals = []
for episode in range(500):
episode_rewards = 0
obs = env.reset()
for step in range(200):
action = basic_policy(obs)
obs, reward, done, info = env.step(action)
episode_rewards += reward
if done:
break
totals.append(episode_rewards)这段代码希望是不言自明的。让我们看看结果:
>>> import numpy as np
>>> np.mean(totals), np.std(totals), np.min(totals), np.max(totals)
(41.718, 8.858356280936096, 24.0, 68.0)即使尝试了 500 次,这项政策也无法使钢管保持直立超过 68 步。不是很好。如果您查看Jupyter notebooks中的模拟,您会发现手推车左右摆动越来越强烈,直到杆倾斜太多。让我们看看神经网络能否提出更好的策略。
神经网络策略
让我们创建神经网络策略。就像我们之前硬编码的策略一样,这个神经网络将观察作为输入,并输出要执行的动作。更准确地说,它将估计每个动作的概率,然后我们将根据估计的概率随机选择一个动作(见图 18-5)。在 CartPole 环境中,只有两种可能的动作(左或右),所以我们只需要一个输出神经元。它将输出动作 0(左)的概率p,当然动作 1(右)的概率为 1 – p。例如,如果它输出 0.7,那么我们将以 70% 的概率选择动作 0,或者以 30% 的概率选择动作 1。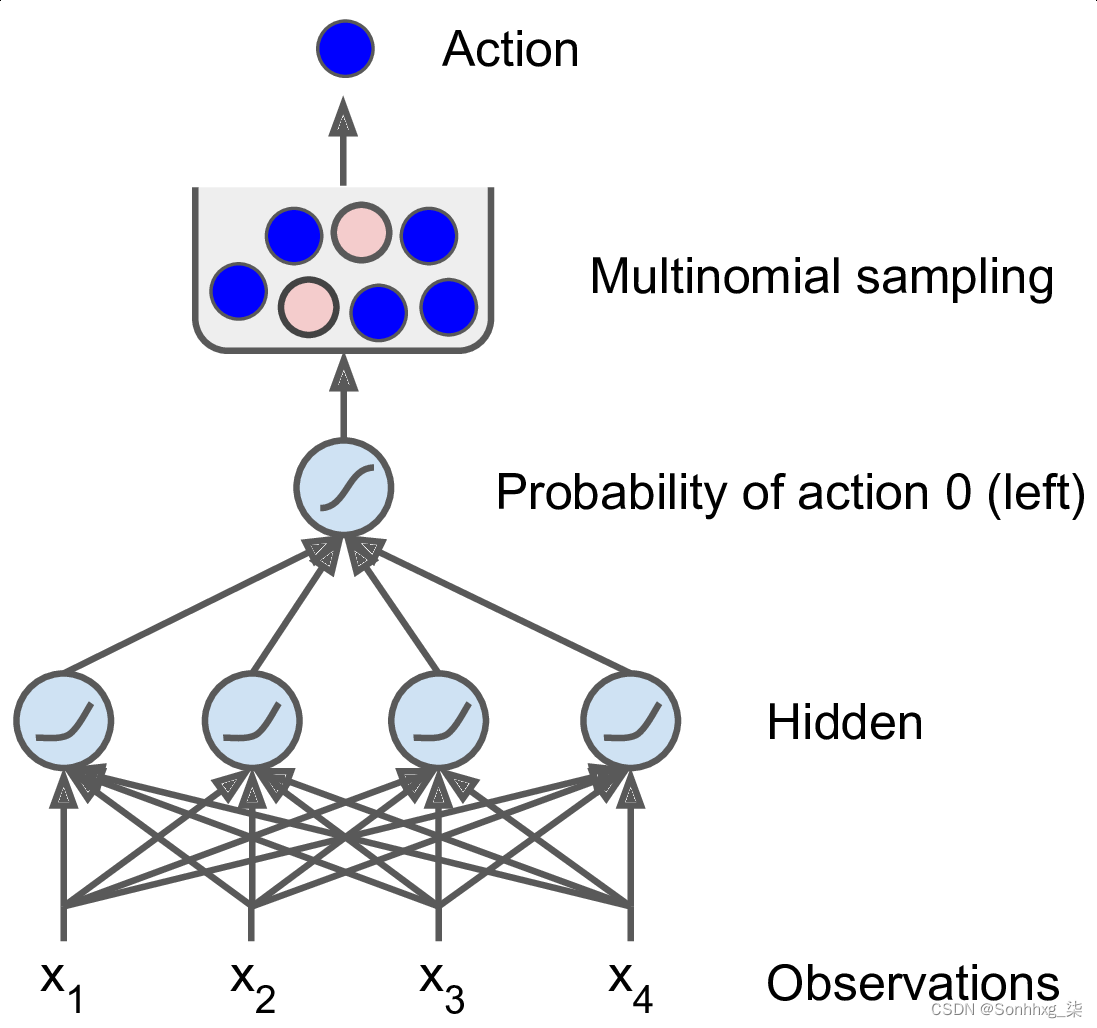
图 18-5。神经网络策略
您可能想知道为什么我们要根据神经网络给出的概率来选择随机动作,而不是仅仅选择得分最高的动作。这个方法让智能体在探索新动作和利用已知有效的动作之间找到适当的平衡。打个比方:假设你第一次去餐馆,所有的菜看起来都一样吸引人,所以你随机挑选一个。如果结果很好,你可以增加你下次点它的概率,但你不应该把这个概率提高到 100%,否则你永远不会尝试其他菜,其中一些可能甚至比你尝试过的更好。
另请注意,在此特定环境中,可以安全地忽略过去的操作和观察,因为每个观察都包含环境的完整状态。如果有一些隐藏状态,那么您可能还需要考虑过去的操作和观察。例如,如果环境只显示了小车的位置而不显示其速度,那么您不仅要考虑当前的观察结果,还要考虑之前的观察结果来估计当前的速度。另一个例子是当观察结果很嘈杂时;在这种情况下,您通常希望使用过去的几次观察来估计最可能的当前状态。因此,CartPole 问题尽可能简单;观察是无噪音的,它们包含环境的完整状态。
以下是使用 tf.keras 构建此神经网络策略的代码:
import tensorflow as tf
from tensorflow import keras
n_inputs = 4 # == env.observation_space.shape[0]
model = keras.models.Sequential([
keras.layers.Dense(5, activation="elu", input_shape=[n_inputs]),
keras.layers.Dense(1, activation="sigmoid"),
])导入后,我们使用一个简单的Sequential模型来定义策略网络。输入的数量是观察空间的大小(在 CartPole 的情况下是 4),我们只有五个隐藏单元,因为这是一个简单的问题。最后,我们要输出一个概率(向左走的概率),所以我们有一个使用 sigmoid 激活函数的输出神经元。如果有两个以上可能的动作,每个动作将有一个输出神经元,我们将使用 softmax 激活函数。
好的,我们现在有一个神经网络策略,它将接受观察并输出动作概率。但是我们如何训练它呢?
评估行动:信用分配问题
如果我们知道每一步的最佳动作是什么,我们可以像往常一样训练神经网络,通过最小化估计的概率分布和目标概率分布之间的交叉熵。这只是常规的监督学习。然而,在强化学习中,智能体获得的唯一指导是通过奖励,而奖励通常是稀疏和延迟的。例如,如果代理设法平衡杆子 100 步,它如何知道它采取的 100 个动作中哪些是好的,哪些是坏的?它只知道最后一个动作之后杆子掉了,但肯定这个最后一个动作并不完全负责。这个被称为信用分配问题:当代理获得奖励时,它很难知道哪些行为应该被归功于(或指责)它。想象一只狗在表现良好后数小时内获得奖励;它会明白它得到什么奖励吗?
至解决这个问题,一种常见的策略是根据其后所有奖励的总和来评估一个动作,通常在每一步应用一个折扣因子 γ (gamma)。折扣奖励的总和称为操作的回报。考虑图 18-6中的示例)。如果一个智能体决定连续 3 次右转,在第一步后得到 +10 奖励,在第二步后得到 0,最后在第三步后得到 –50,那么假设我们使用折扣因子γ = 0.8,第一步动作将返回 10 + γ × 0 + γ 2× (–50) = –22。如果折扣因子接近 0,那么与即时奖励相比,未来的奖励将不重要。相反,如果折扣因子接近 1,那么远在未来的奖励将几乎与即时奖励一样多。典型的折扣系数从 0.9 到 0.99 不等。折扣系数为 0.95 时,未来 13 步的奖励大约是即时奖励的一半(因为 0.95 13 ≈ 0.5),而折扣系数为 0.99 时,未来 69 步的奖励大约是即时奖励的一半即时奖励。在 CartPole 环境中,动作具有相当短期的影响,因此选择 0.95 的折扣因子似乎是合理的。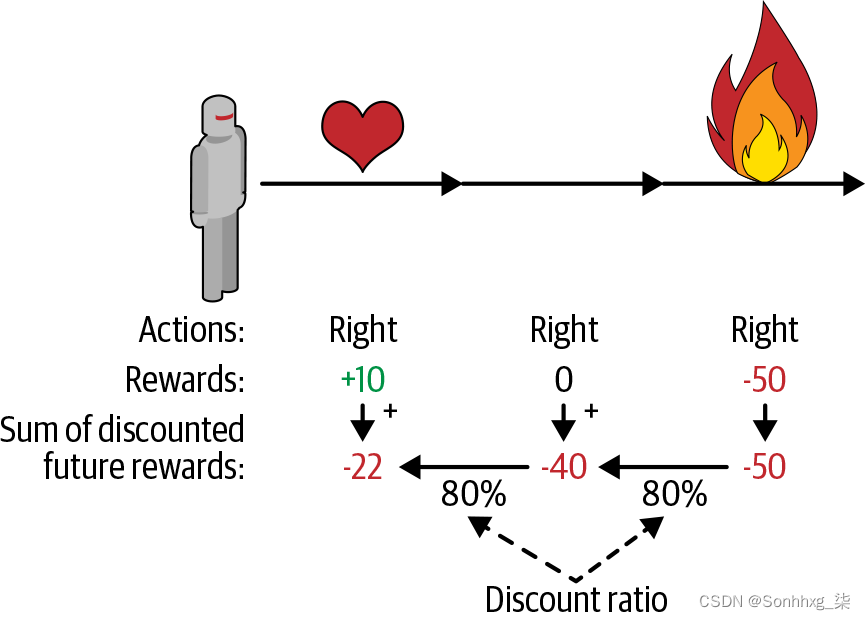
图 18-6。计算一个动作的回报:折扣未来奖励的总和
当然,一个好的动作可能后面跟着几个坏的动作,导致杆子迅速下落,导致好的动作得到低回报(同样,一个好演员有时可能会出演一部糟糕的电影)。但是,如果我们玩游戏的次数足够多,平均而言,好的操作会比坏的操作获得更高的回报。我们想要估计一个动作与其他可能的动作相比平均好多少或差多少。这个称为行动优势。为此,我们必须运行许多集并对所有动作返回进行归一化(通过减去均值并除以标准差)。之后,我们可以合理地假设具有负优势的行为是坏的,而具有正优势的行为是好的。完美——现在我们有了评估每个动作的方法,我们已经准备好使用策略梯度训练我们的第一个代理了。让我们看看如何。
政策梯度
作为前面讨论过,PG 算法通过遵循更高奖励的梯度来优化策略的参数。一类流行的 PG 算法,称为REINFORCE 算法,由 Ronald Williams于 1992 年11年推出。这是一种常见的变体:
-
首先,让神经网络策略玩几次游戏,并在每一步计算梯度,使选择的动作更有可能——但不要应用这些梯度。
-
一旦你运行了几集,计算每个动作的优势(使用上一节中描述的方法)。
-
如果一个动作的优势是积极的,这意味着该动作可能是好的,并且您希望应用之前计算的梯度以使该动作在未来更有可能被选择。但是,如果该动作的优势为负,则意味着该动作可能很糟糕,并且您希望应用相反的梯度以使该动作在未来不太可能发生。解决方案是简单地将每个梯度向量乘以相应动作的优势。
-
最后,计算所有结果梯度向量的平均值,并使用它来执行梯度下降步骤。
让我们使用 tf.keras 来实现这个算法。我们将训练我们之前构建的神经网络策略,以便它学会平衡推车上的杆子。首先,我们需要一个可以播放一步的函数。我们现在假设它采取的任何动作都是正确的,这样我们就可以计算损失及其梯度(这些梯度只会保存一段时间,我们稍后会根据动作的好坏进行修改出来):
def play_one_step(env, obs, model, loss_fn):
with tf.GradientTape() as tape:
left_proba = model(obs[np.newaxis])
action = (tf.random.uniform([1, 1]) > left_proba)
y_target = tf.constant([[1.]]) - tf.cast(action, tf.float32)
loss = tf.reduce_mean(loss_fn(y_target, left_proba))
grads = tape.gradient(loss, model.trainable_variables)
obs, reward, done, info = env.step(int(action[0, 0].numpy()))
return obs, reward, done, grads让我们来看看这个函数:
-
在
GradientTape块中(参见第 12 章),我们首先调用模型,给它一个观察值(我们重塑观察结果,使它成为一个包含单个实例的批次,因为模型需要一个批次)。这输出了向左走的概率。 -
接下来,我们对 0 和 1 之间的随机浮点数进行采样,并检查它是否大于
left_proba。将action与False概率left_proba,或True与概率1 - left_proba。一旦我们将此布尔值转换为一个数字,动作将是 0(左)或 1(右)并具有适当的概率。 -
接下来,我们定义向左走的目标概率:它是 1 减去动作(转换为浮点数)。如果动作为 0(左),则向左的目标概率为 1。如果动作为 1(右),则目标概率为 0。
-
然后我们使用给定的损失函数计算损失,并使用磁带计算关于模型可训练变量的损失梯度。同样,在我们应用它们之前,这些渐变将在稍后进行调整,具体取决于操作结果的好坏。
-
最后,我们播放选定的动作,并返回新的观察、奖励、剧集是否结束,当然还有我们刚刚计算的梯度。
现在让我们创建另一个函数,该函数将依赖该play_one_step()函数来播放多个剧集,返回每个剧集和每一步的所有奖励和梯度:
def play_multiple_episodes(env, n_episodes, n_max_steps, model, loss_fn):
all_rewards = []
all_grads = []
for episode in range(n_episodes):
current_rewards = []
current_grads = []
obs = env.reset()
for step in range(n_max_steps):
obs, reward, done, grads = play_one_step(env, obs, model, loss_fn)
current_rewards.append(reward)
current_grads.append(grads)
if done:
break
all_rewards.append(current_rewards)
all_grads.append(current_grads)
return all_rewards, all_grads此代码返回奖励列表列表(每集一个奖励列表,每步包含一个奖励),以及梯度列表列表(每集一个梯度列表,每个包含每个步骤的一个梯度元组,每个元组包含一个每个可训练变量的梯度张量)。
该算法将使用该play_multiple_episodes()函数玩游戏几次(例如,10 次),然后它会返回并查看所有奖励,将它们打折,并将它们归一化。为此,我们需要更多的函数:第一个将计算每一步的未来折扣奖励的总和,第二个将通过减去均值并除以标准差来标准化许多集的所有这些折扣奖励(回报):
def discount_rewards(rewards, discount_factor):
discounted = np.array(rewards)
for step in range(len(rewards) - 2, -1, -1):
discounted[step] += discounted[step + 1] * discount_factor
return discounted
def discount_and_normalize_rewards(all_rewards, discount_factor):
all_discounted_rewards = [discount_rewards(rewards, discount_factor)
for rewards in all_rewards]
flat_rewards = np.concatenate(all_discounted_rewards)
reward_mean = flat_rewards.mean()
reward_std = flat_rewards.std()
return [(discounted_rewards - reward_mean) / reward_std
for discounted_rewards in all_discounted_rewards]让我们检查一下这是否有效:
>>> discount_rewards([10, 0, -50], discount_factor=0.8)
array([-22, -40, -50])
>>> discount_and_normalize_rewards([[10, 0, -50], [10, 20]],
... discount_factor=0.8)
...
[array([-0.28435071, -0.86597718, -1.18910299]),
array([1.26665318, 1.0727777 ])]调用discount_rewards()返回的正是我们所期望的(见图 18-6)。您可以验证该函数discount_and_normalize_rewards()确实返回了两集中每个动作的标准化动作优势。请注意,第一集比第二集差得多,因此它的归一化优势都是负面的;第一集中的所有动作都被认为是坏的,相反,第二集中的所有动作都被认为是好的。
我们几乎准备好运行算法了!现在让我们定义超参数。我们将运行 150 次训练迭代,每次迭代播放 10 集,每集将持续最多 200 步。我们将使用 0.95 的折扣因子:
n_iterations = 150
n_episodes_per_update = 10
n_max_steps = 200
discount_factor = 0.95我们还需要一个优化器和损失函数。学习率 0.01 的常规 Adam 优化器就可以了,我们将使用二元交叉熵损失函数,因为我们正在训练二元分类器(有两种可能的动作:左或右):
optimizer = keras.optimizers.Adam(lr=0.01)
loss_fn = keras.losses.binary_crossentropy我们现在已经准备好构建和运行训练循环了!
for iteration in range(n_iterations):
all_rewards, all_grads = play_multiple_episodes(
env, n_episodes_per_update, n_max_steps, model, loss_fn)
all_final_rewards = discount_and_normalize_rewards(all_rewards,
discount_factor)
all_mean_grads = []
for var_index in range(len(model.trainable_variables)):
mean_grads = tf.reduce_mean(
[final_reward * all_grads[episode_index][step][var_index]
for episode_index, final_rewards in enumerate(all_final_rewards)
for step, final_reward in enumerate(final_rewards)], axis=0)
all_mean_grads.append(mean_grads)
optimizer.apply_gradients(zip(all_mean_grads, model.trainable_variables))让我们看一下这段代码:
-
在每次训练迭代中,此循环调用该
play_multiple_episodes()函数,该函数玩游戏 10 次,并返回每个情节和步骤的所有奖励和梯度。 -
然后我们调用
discount_and_normalize_rewards()来计算每个动作的标准化优势(在代码中我们称之为final_reward)。事后看来,这提供了一个衡量每个行动实际好坏的衡量标准。 -
接下来,我们遍历每个可训练变量,并为每个变量计算该变量在所有情节和所有步骤中的梯度加权平均值,由
final_reward. -
最后,我们使用优化器应用这些平均梯度:模型的可训练变量将被调整,希望策略会更好一些。
我们完成了!这段代码将训练神经网络策略,它会成功地学会平衡推车上的杆子(你可以在 Jupyter notebook 的“Policy Gradients”部分尝试一下)。每集的平均奖励将非常接近 200(这是此环境的默认最大值)。成功!
小费
即使代理最初对环境一无所知,研究人员也试图找到运行良好的算法。但是,除非您正在撰写论文,否则您应该毫不犹豫地将先验知识注入到代理中,因为这将大大加快训练速度。例如,由于您知道杆应该尽可能垂直,您可以添加与杆的角度成比例的负奖励。这将使奖励变得不那么稀疏并加快训练速度。此外,如果您已经有一个相当好的策略(例如,硬编码),您可能希望在使用策略梯度来改进它之前训练神经网络来模仿它。
这我们刚刚训练的简单策略梯度算法解决了 CartPole 任务,但它不能很好地扩展到更大和更复杂的任务。确实,它的样本效率非常低,这意味着它需要对游戏进行很长时间的探索才能取得重大进展。这是因为它必须运行多个情节来估计每个动作的优势,正如我们所看到的。然而,它是更强大算法的基础,例如Actor-Critic算法(我们将在本章末尾简要讨论)。
我们现在来看看另一个流行的算法家族。虽然 PG 算法直接尝试优化策略以增加奖励,但我们现在要研究的算法不那么直接:代理学习估计每个状态的预期回报,或者每个状态中的每个动作,然后它使用这些知识来决定如何行动。要理解这些算法,我们首先要介绍马尔可夫决策过程。
马尔可夫决策过程
在20世纪初,数学家安德烈·马尔科夫研究了没有记忆的随机过程,称为 马尔可夫链。这样的过程具有固定数量的状态,并且在每个步骤中随机地从一种状态演变为另一种状态。它从状态s演化到状态s ' 的概率是固定的,它只取决于对 ( s , s '),而不取决于过去的状态(这就是我们说系统没有记忆的原因)。
图 18-7显示了一个具有四个状态的马尔可夫链的示例。
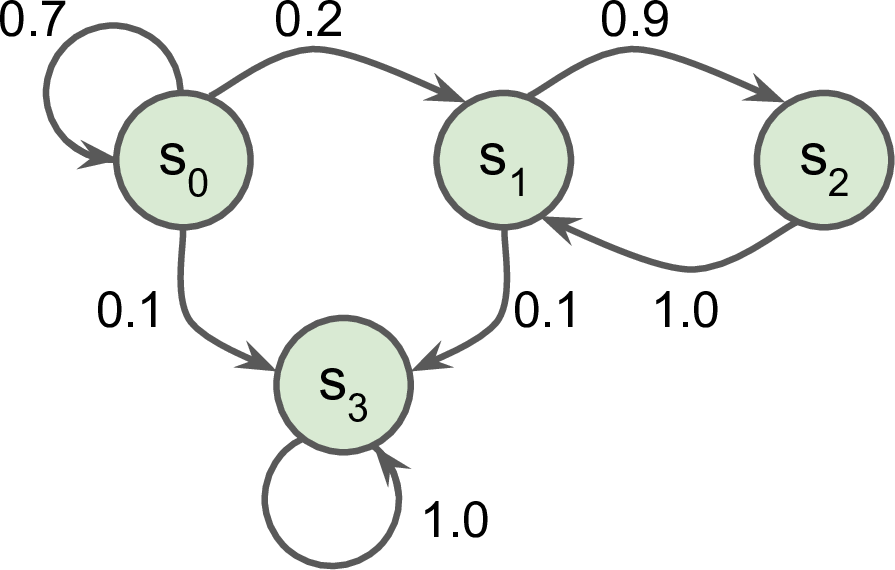
图 18-7。马尔可夫链示例
假设流程从状态s 0开始,并且有 70% 的机会在下一步将保持在该状态。最终它必然会离开那个状态并且永远不会回来,因为没有其他状态指向s 0。如果它进入状态s 1,那么它很可能会进入状态s 2(90% 的概率),然后立即回到状态s 1(有 100% 的概率)。它可能会在这两种状态之间交替多次,但最终会落入状态s 3并保持永远存在(这是一个终端状态)。马尔可夫链可以有非常不同的动力学,它们大量用于热力学、化学、统计学等等。
1950 年代,Richard Bellman 首次描述了马尔可夫决策过程。12它们类似于马尔可夫链,但有一个转折点:在每一步,代理可以选择几个可能的动作之一,转移概率取决于所选动作。此外,一些状态转换会返回一些奖励(正或负),并且代理的目标是找到一个随着时间的推移最大化奖励的策略。
例如,图 18-8中表示的 MDP具有三个状态(用圆圈表示)和每个步骤最多三个可能的离散动作(用菱形表示)。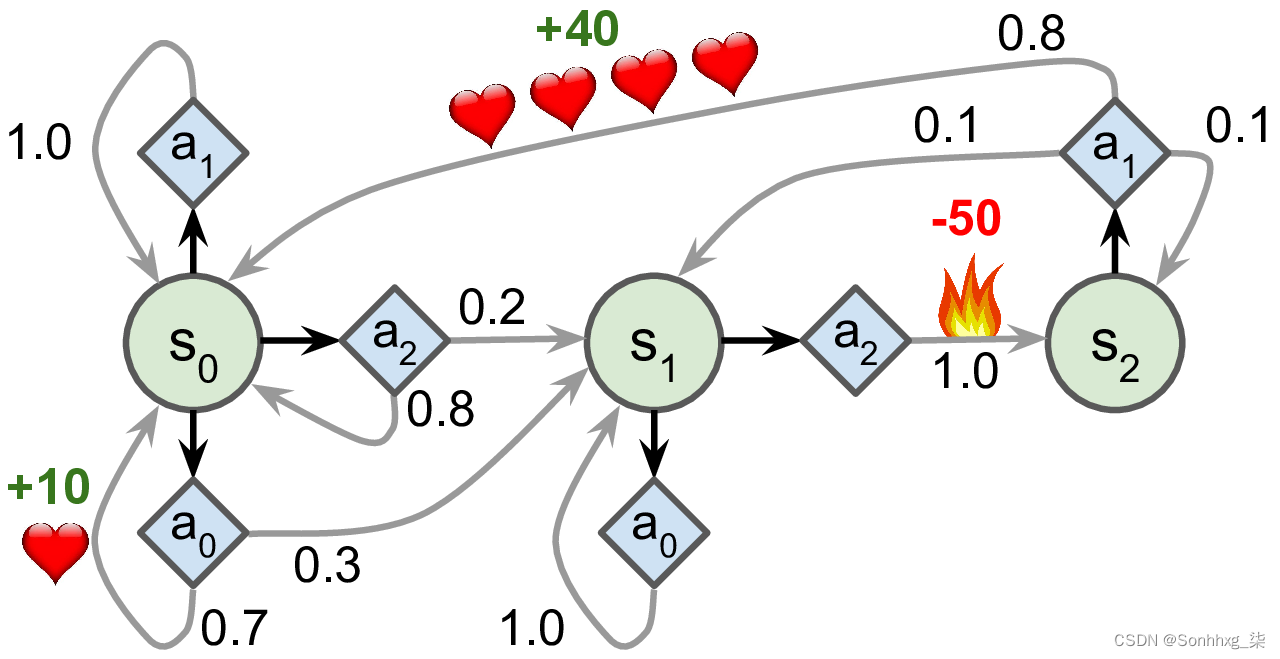
图 18-8。马尔可夫决策过程示例
如果它从状态s 0开始,代理可以在动作a 0、a 1或a 2之间进行选择。如果它选择动作a 1,它只是确定地保持在状态s 0,并且没有任何奖励。因此,如果它愿意,它可以决定永远呆在那里。但如果它选择动作a 0,它有 70% 的概率获得 +10 的奖励并保持在状态s 0。然后它可以一次又一次地尝试获得尽可能多的奖励,但在某一时刻它最终会进入状态s 1。在状态s1它只有两种可能的动作:a 0或a 2。它可以通过重复选择动作a 0来选择保持原状,或者它可以选择继续进入状态s 2并获得 –50 的负奖励(哎哟)。在状态s 2中,它别无选择,只能采取行动a 1,这很可能会导致它回到状态s 0,并在途中获得 +40 的奖励。你得到图片。通过查看这个 MDP,您能猜出哪个策略会随着时间的推移获得最大的回报吗?在状态s 0很明显,动作a 0是最好的选择,并且在状态s 2中,智能体别无选择,只能采取行动a 1,但在状态s 1中,智能体应该留在原地( a 0)还是过火(a 2)并不明显.
贝尔曼找到了一种估计任何状态s的最佳状态值的方法,注意到V *( s ),它是代理在达到状态s后平均可以期望的所有折扣未来奖励的总和,假设它的行为最佳。他表明,如果代理行为最佳,那么贝尔曼最优方程适用(见方程18-1)。这个递归方程表明,如果代理行为最优,那么当前状态的最优值等于它在采取一个最优动作后平均获得的奖励,加上该动作可能导致的所有可能的下一个状态的预期最优值至。
公式 18-1。贝尔曼最优方程
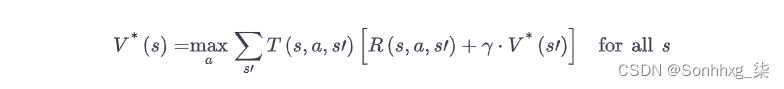
在这个等式中:
-
T ( s , a , s ') 是从状态s到状态s ' 的转移概率,假设智能体选择了动作a。例如,在图 18-8中,T ( s 2 , a 1 , s 0 ) = 0.8。
-
R ( s , a , s ') 是代理从状态s进入状态s时获得的奖励,假设代理选择了动作a。例如,在图 18-8中,R ( s 2 , a 1 , s 0 ) = +40。
-
γ是折扣因子。
这个等式直接导致了一种算法,可以精确估计每个可能状态的最优状态值:首先将所有状态值估计初始化为零,然后迭代更新它们使用值迭代算法(见公式 18-2)。一个显着的结果是,只要有足够的时间,这些估计就可以保证收敛到与最优策略相对应的最优状态值。
公式 18-2。值迭代算法
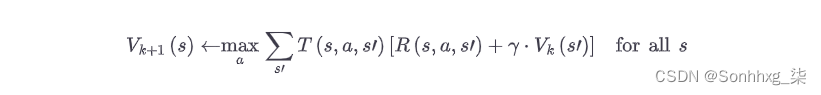
在这个等式中,V k ( s ) 是算法第k次迭代时状态s的估计值。
会心最优状态值可能很有用,尤其是在评估策略时,但它并没有为我们提供代理的最优策略。幸运的是,Bellman 发现了一种非常相似的算法来估计最优状态动作值,通常称为Q-Values(质量值)。状态-动作对 ( s , a ) 的最优 Q 值,记为Q *( s , a ),是智能体在达到状态s并选择动作a后平均可以预期的贴现未来奖励的总和,但在它看到这个动作的结果之前,假设它在那个动作之后采取了最佳行动。
这里它是如何工作的:再一次,首先将所有 Q 值估计初始化为零,然后使用Q 值迭代算法更新它们(参见公式 18-3)。
公式 18-3。Q值迭代算法

让我们将此算法应用于图 18-8中表示的 MDP 。首先,我们需要定义 MDP:
transition_probabilities = [ # shape=[s, a, s']
[[0.7, 0.3, 0.0], [1.0, 0.0, 0.0], [0.8, 0.2, 0.0]],
[[0.0, 1.0, 0.0], None, [0.0, 0.0, 1.0]],
[None, [0.8, 0.1, 0.1], None]]
rewards = [ # shape=[s, a, s']
[[+10, 0, 0], [0, 0, 0], [0, 0, 0]],
[[0, 0, 0], [0, 0, 0], [0, 0, -50]],
[[0, 0, 0], [+40, 0, 0], [0, 0, 0]]]
possible_actions = [[0, 1, 2], [0, 2], [1]]例如,要知道在执行动作a 1后从s 2到s 0的转移概率,我们将查找(即 0.8)。同样,要获得相应的奖励,我们会查找(即+40)。为了获得s 2中可能的动作列表,我们将查找(在这种情况下,只有动作a 1是可能的)。接下来,我们必须将所有 Q 值初始化为 0(除了不可能的动作,我们将 Q 值设置为 –∞):transition_probabilities[2][1][0]rewards[2][1][0]possible_actions[2]
Q_values = np.full((3, 3), -np.inf) # -np.inf for impossible actions
for state, actions in enumerate(possible_actions):
Q_values[state, actions] = 0.0 # for all possible actions现在让我们运行 Q 值迭代算法。它将公式 18-3重复应用于所有 Q 值,用于每个状态和每个可能的动作:
gamma = 0.90 # the discount factor
for iteration in range(50):
Q_prev = Q_values.copy()
for s in range(3):
for a in possible_actions[s]:
Q_values[s, a] = np.sum([
transition_probabilities[s][a][sp]
* (rewards[s][a][sp] + gamma * np.max(Q_prev[sp]))
for sp in range(3)])而已!生成的 Q 值如下所示:
>>> Q_values
array([[18.91891892, 17.02702702, 13.62162162],
[ 0. , -inf, -4.87971488],
[ -inf, 50.13365013, -inf]])例如,当代理处于状态s 0并且它选择动作a 1时,预期的折扣未来奖励总和约为 17.0。
对于每个状态,让我们看看具有最高 Q 值的动作:
>>> np.argmax(Q_values, axis=1) # optimal action for each state
array([0, 0, 1])这给了我们这个 MDP 的最优策略,当使用 0.90 的折扣因子时:在状态s 0选择动作a 0;在状态s 1中选择动作a 0(即,保持原状);并且在状态s 2中选择动作a 1(唯一可能的动作)。有趣的是,如果我们将折扣因子增加到 0.95,则最优策略会发生变化:在状态s 1中,最佳动作变为2(去火!)。这是有道理的,因为你越重视未来的回报,你就越愿意为了未来幸福的承诺而忍受现在的一些痛苦。
时间差异学习
强化学习离散动作的问题通常可以建模为马尔可夫决策过程,但代理最初不知道转移概率是多少(它不知道T ( s , a , s ′)),也不知道奖励是什么要么是(它不知道R ( s , a , s '))。它必须至少经历一次每个状态和每个转换才能知道奖励,并且它必须经历多次才能对转换概率进行合理估计。
时间差分学习(TD Learning) 算法与值迭代算法非常相似,但进行了调整以考虑到代理仅了解 MDP 的一部分这一事实。一般来说,我们假设代理最初只知道可能的状态和动作,仅此而已。这代理使用探索策略(例如,纯随机策略)来探索 MDP,并且随着它的进展,TD 学习算法根据实际观察到的转换和奖励更新状态值的估计(参见公式 18- 4)。
公式 18-4。TD 学习算法
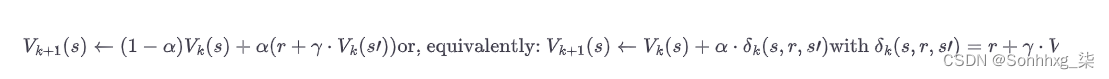
在这个等式中:
写这个方程的第一种形式的更简洁的方法是使用符号一个←一个b, 这意味着a k +1 ← (1 – α ) · a k + α · b k。因此,公式 18-4的第一行可以改写如下:在(s)←一个r+C·在(s').
小费
TD Learning 与随机梯度下降有许多相似之处,特别是它一次处理一个样本这一事实。此外,就像随机 GD 一样,只有逐渐降低学习率,它才能真正收敛(否则它会一直在最优 Q 值附近反弹)。
对于每个状态s,该算法仅跟踪代理在离开该状态时获得的即时奖励的运行平均值,以及它期望稍后获得的奖励(假设它以最佳方式运行)。
Q-学习
同样,Q-Learning 算法是 Q 值迭代算法对转移概率和奖励最初未知的情况的改编(参见公式 18-5)。Q-Learning 的工作原理是观察智能体的游戏(例如,随机地)并逐渐改进其对 Q 值的估计。一旦它有准确的 Q 值估计(或足够接近),那么最优策略就是选择具有最高 Q 值的动作(即贪心策略)。
公式 18-5。Q-学习算法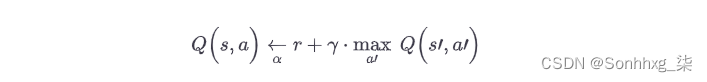
对于每个状态-动作对 ( s , a ),该算法跟踪代理在离开状态s时获得的奖励r的运行平均值,以及它期望获得的折扣未来奖励的总和。为了估计这个总和,我们取下一个状态s ' 的 Q 值估计的最大值,因为我们假设目标策略从那时起会采取最佳行动。
让我们实现 Q-Learning 算法。首先,我们需要让代理探索环境。为此,我们需要一个阶跃函数,以便代理可以执行一个动作并获得结果状态和奖励:
def step(state, action):
probas = transition_probabilities[state][action]
next_state = np.random.choice([0, 1, 2], p=probas)
reward = rewards[state][action][next_state]
return next_state, reward现在让我们实现代理的探索策略。由于状态空间非常小,一个简单的随机策略就足够了。如果我们运行算法足够长的时间,代理将多次访问每个状态,并且还会多次尝试每个可能的动作:
def exploration_policy(state):
return np.random.choice(possible_actions[state])接下来,在我们像之前一样初始化 Q-Values 之后,我们准备运行具有学习率衰减的 Q-Learning 算法(使用功率调度,在第 11 章中介绍):
alpha0 = 0.05 # initial learning rate
decay = 0.005 # learning rate decay
gamma = 0.90 # discount factor
state = 0 # initial state
for iteration in range(10000):
action = exploration_policy(state)
next_state, reward = step(state, action)
next_value = np.max(Q_values[next_state])
alpha = alpha0 / (1 + iteration * decay)
Q_values[state, action] *= 1 - alpha
Q_values[state, action] += alpha * (reward + gamma * next_value)
state = next_state该算法将收敛到最佳 Q 值,但需要多次迭代,并且可能需要大量的超参数调整。如图18-9 所示,Q-Value 迭代算法(左)收敛速度非常快,不到 20 次迭代,而 Q-Learning 算法(右)大约需要 8,000 次迭代才能收敛。显然,不知道转移概率或奖励会使找到最优策略变得更加困难!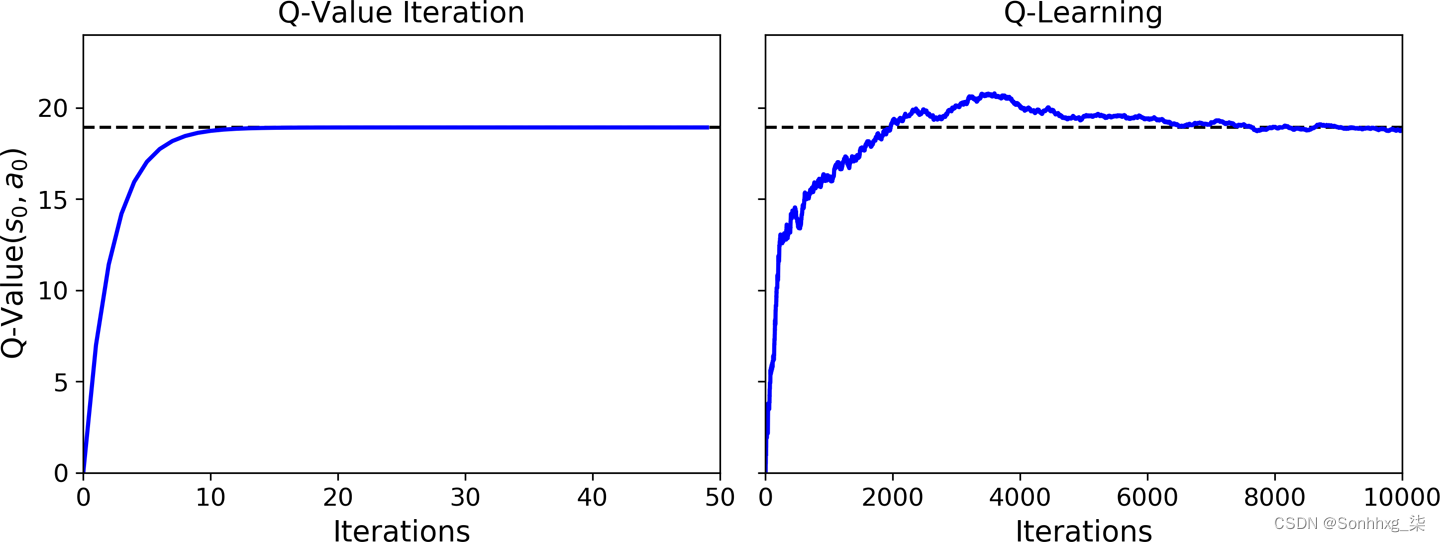
图 18-9。Q-Value 迭代算法(左)与 Q-Learning 算法(右)
这Q-Learning 算法被称为离策略算法,因为被训练的策略不一定是正在执行的策略:在前面的代码示例中,正在执行的策略(探索策略)是完全随机的,而正在训练的策略将始终选择具有最高 Q 值的动作。相反,策略梯度algorithm 是一种on-policy算法:它使用正在训练的策略探索世界。令人惊讶的是,Q-Learning 能够通过观察智能体的随机行为来学习最优策略(想象一下当你的老师是一只喝醉的猴子时学习打高尔夫球)。我们能做得更好吗?
勘探政策
的当然,只有探索策略对 MDP 的探索足够彻底,Q-Learning 才能发挥作用。虽然一个纯粹随机的策略保证最终会多次访问每个状态和每个转换,但这样做可能需要非常长的时间。因此,更好的选择是使用ε-greedy 策略(ε 是 epsilon):在每一步它以概率ε随机行动,或者以概率 1 - ε贪婪地行动(即选择具有最高 Q 值的动作)。ε的优点-贪婪策略(与完全随机的策略相比)是它将花费越来越多的时间探索环境中有趣的部分,因为 Q 值估计越来越好,同时仍然花费一些时间访问 MDP 的未知区域. 从ε的高值(例如,1.0)开始,然后逐渐降低它(例如,降至 0.05)是很常见的。
或者,不是仅仅依靠探索的机会,另一种方法是鼓励探索策略尝试它以前没有尝试过的动作。这可以作为添加到 Q 值估计的奖励来实现,如公式 18-6所示。
公式 18-6。使用探索功能的 Q-Learning
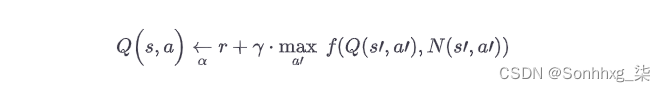
在这个等式中:
-
N ( s ', a ') 计算在状态s ' 中选择动作a ' 的次数。
-
f ( Q , N ) 是一个探索函数,例如f ( Q , N ) = Q + κ /(1 + N ),其中κ是一个好奇心超参数,用于衡量智能体对未知事物的吸引力程度。
近似 Q 学习和深度 Q 学习
这Q-Learning 的主要问题是它不能很好地扩展到具有许多状态和动作的大型(甚至中等)MDP。例如,假设您想使用 Q-Learning 来训练代理玩吃豆人小姐(见图 18-1)。吃豆人女士可以吃大约 150 个颗粒,每个颗粒都可以存在或不存在(即,已经吃过)。因此,可能的状态数大于 2 150 ≈ 10 45。如果你将所有幽灵和吃豆人女士的所有可能位置组合相加,可能状态的数量就会超过我们星球上的原子数量,所以你绝对无法跟踪估计每一个 Q 值。
解决方案是找到一个函数Q θ ( s , a ),它使用可管理数量的参数(由参数向量θ给出)逼近任何状态-动作对 ( s , a ) 的 Q 值。这称为近似 Q 学习。多年来,建议使用从状态中提取的手工特征的线性组合(例如,最近的鬼魂的距离、它们的方向等)来估计 Q 值,但在 2013 年,DeepMind表明使用深度神经网络可以工作得更好,特别是对于复杂的问题,它不需要任何特征工程。一个用于估计 Q-Values 的 DNN 称为Deep Q-Network (DQN),使用 DQN 进行 Approximate Q-Learning 称为Deep Q-Learning。
现在,我们如何训练 DQN?好吧,考虑一下 DQN 为给定的状态-动作对 ( s , a ) 计算的近似 Q 值。感谢 Bellman,我们知道我们希望这个近似的 Q 值尽可能接近我们在状态s下执行动作a后实际观察到的奖励r,加上从那时起以最佳方式玩的折扣值。为了估计这个未来折扣奖励的总和,我们可以简单地在下一个状态s ' 上执行 DQN,并且对于所有可能的动作a'。我们为每个可能的动作得到一个近似的未来 Q 值。然后我们选择最高的(因为我们假设我们会以最佳方式玩)并对其进行折扣,这为我们提供了对未来折扣奖励总和的估计。通过将奖励r和未来贴现值估计相加,我们得到状态-动作对 ( s , a ) 的目标 Q 值y ( s , a ),如公式 18-7所示。
公式 18-7。目标 Q 值
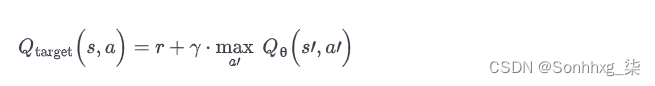
有了这个目标 Q 值,我们可以使用任何梯度下降算法运行训练步骤。具体来说,我们一般会尽量减少估计的 Q-Value Q ( s , a ) 与目标 Q-Value 之间的平方误差(或 Huber loss 以降低算法对大误差的敏感性)。这就是基本的深度 Q 学习算法的全部内容!让我们看看如何实现它来解决 CartPole 环境。
实施深度 Q 学习
这我们需要的第一件事是深度 Q 网络。从理论上讲,您需要一个接受状态-动作对并输出近似 Q 值的神经网络,但在实践中,使用接受状态并为每个可能的操作输出一个近似 Q 值的神经网络要高效得多. 要解决 CartPole 环境,我们不需要非常复杂的神经网络;几个隐藏层就可以了:
env = gym.make("CartPole-v0")
input_shape = [4] # == env.observation_space.shape
n_outputs = 2 # == env.action_space.n
model = keras.models.Sequential([
keras.layers.Dense(32, activation="elu", input_shape=input_shape),
keras.layers.Dense(32, activation="elu"),
keras.layers.Dense(n_outputs)
])为了使用这个 DQN 选择一个动作,我们选择具有最大预测 Q 值的动作。为了确保智能体探索环境,我们将使用ε -贪婪策略(即,我们将选择概率为ε的随机动作):
def epsilon_greedy_policy(state, epsilon=0):
if np.random.rand() < epsilon:
return np.random.randint(2)
else:
Q_values = model.predict(state[np.newaxis])
return np.argmax(Q_values[0])我们不会仅根据最新经验训练 DQN,而是将存储重放缓冲区(或重放内存)中的所有经验,我们将在每次训练迭代中从中抽取一个随机训练批次。这有助于减少训练批次中体验之间的相关性,这极大地有助于训练。为此,我们将只使用一个双端队列列表:
from collections import deque
replay_buffer = deque(maxlen=2000)小费
每个体验将由五个元素组成:一个状态、代理采取的行动、产生的奖励、它到达的下一个状态,最后是一个布尔值,指示情节是否在该点结束 ( done)。我们需要一个小函数来从回放缓冲区中随机抽取一批体验。它将返回与五个体验元素对应的五个 NumPy 数组:
def sample_experiences(batch_size):
indices = np.random.randint(len(replay_buffer), size=batch_size)
batch = [replay_buffer[index] for index in indices]
states, actions, rewards, next_states, dones = [
np.array([experience[field_index] for experience in batch])
for field_index in range(5)]
return states, actions, rewards, next_states, dones让我们还创建一个函数,该函数将使用ε -greedy 策略播放单个步骤,然后将结果体验存储在重放缓冲区中:
def play_one_step(env, state, epsilon):
action = epsilon_greedy_policy(state, epsilon)
next_state, reward, done, info = env.step(action)
replay_buffer.append((state, action, reward, next_state, done))
return next_state, reward, done, info最后,让我们创建最后一个函数,该函数将从回放缓冲区中采样一批经验,并通过对这批数据执行单个梯度下降步骤来训练 DQN:
batch_size = 32
discount_factor = 0.95
optimizer = keras.optimizers.Adam(lr=1e-3)
loss_fn = keras.losses.mean_squared_error
def training_step(batch_size):
experiences = sample_experiences(batch_size)
states, actions, rewards, next_states, dones = experiences
next_Q_values = model.predict(next_states)
max_next_Q_values = np.max(next_Q_values, axis=1)
target_Q_values = (rewards +
(1 - dones) * discount_factor * max_next_Q_values)
target_Q_values = target_Q_values.reshape(-1, 1)
mask = tf.one_hot(actions, n_outputs)
with tf.GradientTape() as tape:
all_Q_values = model(states)
Q_values = tf.reduce_sum(all_Q_values * mask, axis=1, keepdims=True)
loss = tf.reduce_mean(loss_fn(target_Q_values, Q_values))
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))让我们看一下这段代码:
-
首先我们定义一些超参数,然后我们创建优化器和损失函数。
-
然后我们创建
training_step()函数。它首先对一批体验进行采样,然后使用 DQN 预测每个体验下一个状态中每个可能动作的 Q 值。由于我们假设代理将处于最佳状态,因此我们只为每个下一个状态保留最大 Q 值。接下来,我们使用公式 18-7计算每个体验的状态-动作对的目标 Q 值。 -
接下来,我们想使用 DQN 来计算每个经历过的状态-动作对的 Q 值。但是,DQN 也会输出其他可能动作的 Q 值,而不仅仅是代理实际选择的动作。所以我们需要屏蔽掉所有不需要的 Q 值。该
tf.one_hot()函数可以轻松地将一组动作索引转换为这样的掩码。例如,如果前三个体验分别包含动作 1、1、0,则掩码将以 开头[[0, 1], [0, 1], [1, 0],...]。然后我们可以将 DQN 的输出与这个掩码相乘,这会将我们不想要的所有 Q 值清零。然后我们在轴 1 上求和以消除所有零,只保留经验状态-动作对的 Q 值。这给了我们Q_values张量,包含批次中每个经验的一个预测 Q 值。 -
最后,我们执行梯度下降步骤以最小化模型可训练变量的损失。
这是最难的部分。现在训练模型很简单:
for episode in range(600):
obs = env.reset()
for step in range(200):
epsilon = max(1 - episode / 500, 0.01)
obs, reward, done, info = play_one_step(env, obs, epsilon)
if done:
break
if episode > 50:
training_step(batch_size)我们运行 600 集,每集最多 200 步。在每一步,我们首先计算ε -greedy 策略的epsilon值:它将在 500 次以下的时间内线性地从 1 下降到 0.01。然后我们调用该函数,它将使用ε -greedy 策略来选择一个动作,然后执行它并将体验记录在回放缓冲区中。如果情节完成,我们退出循环。最后,如果我们超过了第 50 集,我们称play_one_step()training_step()函数在从回放缓冲区采样的一批上训练模型。我们在没有训练的情况下播放 50 集的原因是给回放缓冲区一些时间来填满(如果我们等待的时间不够长,那么回放缓冲区中将没有足够的多样性)。就是这样,我们刚刚实现了深度 Q 学习算法!
图 18-10显示了智能体在每一集中获得的总奖励。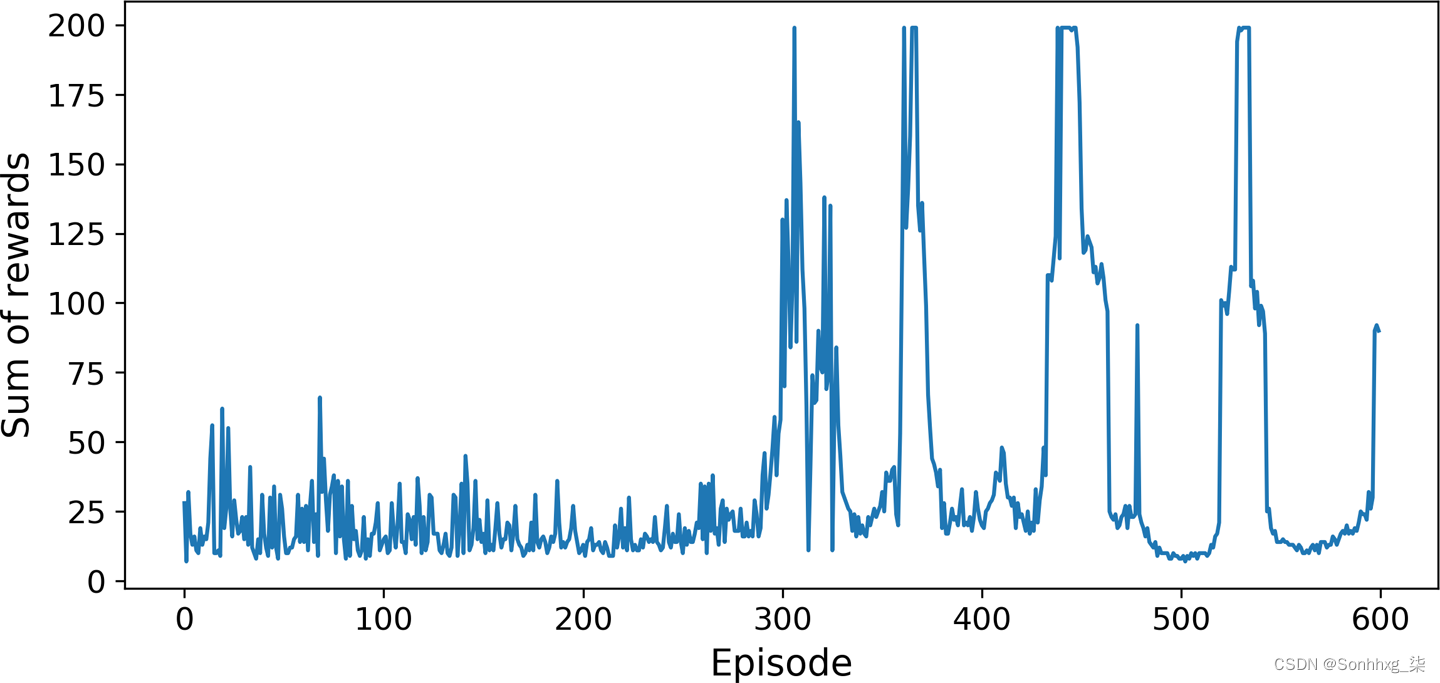
图 18-10。Deep Q-Learning 算法的学习曲线
如您所见,该算法在将近 300 集内没有任何明显进展(部分原因是一开始ε非常高),然后其性能突然飙升至 200(这是该环境下可能的最大性能)。这是个好消息:该算法运行良好,而且它实际上运行得比策略梯度算法快得多!但是等等……仅仅几集之后,它就忘记了它所知道的一切,它的表现下降到了25以下!这个被称为灾难性遗忘,这是几乎所有 RL 算法面临的大问题之一:当代理探索环境时,它会更新其策略,但它在环境的一个部分中学到的东西可能会破坏它在环境的其他部分中早先学到的东西。体验非常相关,学习环境也在不断变化——这对于梯度下降来说并不理想!如果增加重放缓冲区的大小,算法将较少受此问题的影响。降低学习率也可能有所帮助。但事实是,强化学习很难:训练通常不稳定,您可能需要尝试许多超参数值和随机种子,然后才能找到效果良好的组合。例如,如果您尝试将前面每层的神经元数量从 32 更改为 30 或 34,
笔记
强化学习是出了名的困难,主要是因为训练的不稳定性以及对超参数值和随机种子选择的巨大敏感性。13正如研究员 Andrej Karpathy 所说:“[监督学习] 想要发挥作用。[…] RL 必须被迫工作。” 你需要时间、耐心、毅力,也许还需要一点运气。这是 RL 不像常规深度学习(例如卷积网络)那样被广泛采用的主要原因。但是除了 AlphaGo 和 Atari 游戏之外,还有一些现实世界的应用:例如,谷歌使用 RL 来优化其数据中心的成本,它被用于一些机器人应用程序、超参数调整和推荐系统中。
您可能想知道为什么我们没有绘制损失图。事实证明,损失是模型性能的一个很差的指标。损失可能会下降,但智能体的表现可能会更差(例如,当智能体卡在环境的一个小区域中时,可能会发生这种情况,并且 DQN 开始过度拟合该区域)。相反,损失可能会增加,但代理可能会表现得更好(例如,如果 DQN 低估了 Q 值,并且它开始正确地增加其预测,代理可能会表现得更好,获得更多奖励,但损失可能增加,因为 DQN 也设置了目标,目标也会更大)。
到目前为止,我们一直使用的基本深度 Q 学习算法太不稳定,无法学习玩 Atari 游戏。那么 DeepMind 是如何做到的呢?好吧,他们调整了算法!
深度 Q 学习变体
让我们看看几个可以稳定和加速训练的 Deep Q-Learning 算法的变体。
固定 Q 值目标
在作为基本的深度 Q 学习算法,该模型既用于进行预测,也用于设置自己的目标。这可能导致类似于狗追逐自己的尾巴的情况。这个反馈回路会使网络变得不稳定:它会发散、振荡、冻结等等。为了解决这个问题,DeepMind 研究人员在他们 2013 年的论文中使用了两个 DQN 而不是一个:第一个是在线模型,它在每一步都学习并用于移动代理,另一个是目标模型,仅用于定义目标。目标模型只是在线模型的克隆:
target = keras.models.clone_model(model)
target.set_weights(model.get_weights())然后,在training_step()函数中,我们只需要在计算下一个状态的 Q-Values 时,更改一行以使用目标模型而不是在线模型:
next_Q_values = target.predict(next_states)最后,在训练循环中,我们必须定期(例如,每 50 集)将在线模型的权重复制到目标模型:
if episode % 50 == 0:
target.set_weights(model.get_weights())由于目标模型的更新频率远低于在线模型,因此 Q 值目标更稳定,我们之前讨论的反馈回路受到抑制,其影响也不那么严重。这种方法是 DeepMind 研究人员在 2013 年论文中的主要贡献之一,它允许代理学习从原始像素玩 Atari 游戏。为了稳定训练,他们使用了 0.00025 的微小学习率,他们仅每 10,000 步更新目标模型(而不是前面代码示例中的 50 步),并且他们使用了一个非常大的重放缓冲区,可容纳 100 万次体验。它们epsilon以非常缓慢的速度下降,从 1 到 0.1 每 100 万步,它们让算法运行了 5000 万步。
在本章后面,我们将使用 TF-Agents 库来训练 DQN 代理使用这些超参数玩Breakout,但在我们到达那里之前,让我们看一下另一个 DQN 变体,它再次成功击败了最先进的技术.
双DQN(Double DQN)
在在2015 年的一篇论文中,14位DeepMind 研究人员调整了他们的 DQN 算法,提高了其性能并在一定程度上稳定了训练。他们称这种变体为Double DQN. 更新是基于观察到目标网络容易高估 Q 值。事实上,假设所有动作都同样好:目标模型估计的 Q 值应该是相同的,但由于它们是近似值,因此某些行为可能会略大于其他行为,纯属偶然。目标模型总是会选择最大的 Q-Value,它会比平均 Q-Value 略大,很可能高估了真实的 Q-Value(有点像在测量波的深度时计算最高随机波的高度)水池)。为了解决这个问题,他们建议在为下一个状态选择最佳动作时使用在线模型而不是目标模型,并且只使用目标模型来估计这些最佳动作的 Q 值。这是更新的training_step()功能:
def training_step(batch_size):
experiences = sample_experiences(batch_size)
states, actions, rewards, next_states, dones = experiences
next_Q_values = model.predict(next_states)
best_next_actions = np.argmax(next_Q_values, axis=1)
next_mask = tf.one_hot(best_next_actions, n_outputs).numpy()
next_best_Q_values = (target.predict(next_states) * next_mask).sum(axis=1)
target_Q_values = (rewards +
(1 - dones) * discount_factor * next_best_Q_values)
mask = tf.one_hot(actions, n_outputs)
[...] # the rest is the same as earlier仅仅几个月后,又提出了对 DQN 算法的另一项改进。
优先体验重播
反而从回放缓冲区中统一采样经验,为什么不更频繁地采样重要经验?这个这个想法被称为重要性采样(IS) 或优先体验重放(PER),它是由 DeepMind 研究人员在2015 年的一篇论文15中引入的(再一次!)。
更具体地说,如果经验可能会导致快速的学习进步,则这些经验被认为是“重要的”。但是我们如何估计呢?一种合理的方法是测量 TD 误差的大小δ = r + γ · V ( s ′) – V ( s )。较大的 TD 误差表明转换 ( s , r , s ′) 非常令人惊讶,因此可能值得学习。16当一个体验被记录在回放缓冲区中时,它的优先级被设置为一个非常大的值,以确保它至少被采样一次。但是,一旦采样(以及每次采样),就会计算 TD 误差δ,并将此体验的优先级设置为p = | δ | (加上一个小常数,以确保每次体验都具有非零抽样概率)。对优先级为p的体验进行采样的概率P与p ζ成正比,其中ζ是一个超参数,用于控制我们希望重要性采样的贪心程度:当ζ = 0 时,我们只会得到均匀采样,而当ζ= 1,我们得到全面的重要性抽样。在论文中,作者使用了ζ = 0.6,但最佳值将取决于任务。
但是有一个问题:由于样本会偏向于重要的经验,我们必须在训练期间通过根据重要性降低经验的权重来补偿这种偏见,否则模型将过度拟合重要的经验。需要明确的是,我们希望更频繁地对重要体验进行采样,但这也意味着我们必须在训练期间给予它们较低的权重。为此,我们将每个体验的训练权重定义为w = ( n P ) – β,其中n是回放缓冲区中的体验数量,而β是一个超参数,控制我们想要补偿重要性采样偏差的程度(0 表示完全没有,而 1 表示完全)。在论文中,作者在训练开始时使用β = 0.4,并在训练结束时将其线性增加到β = 1。同样,最佳值将取决于任务,但如果您增加一个,您通常也希望增加另一个。
现在让我们看一下 DQN 算法的最后一个重要变体。
决斗DQN(Dueling DQN)
Dueling DQN算法(DDQN,不要与双 DQN 混淆,尽管这两种技术可以很容易地结合使用)是DeepMind 研究人员在2015年的另一篇论文17中介绍的。要理解它是如何工作的,我们必须首先注意到状态-动作对 ( s , a ) 的 Q-Value 可以表示为Q ( s , a ) = V ( s ) + A ( s , a ),其中V ( s ) 是状态s的值,A ( s , a ) 是优势在状态s中采取行动a与该状态下所有其他可能的行动相比。此外,一个状态的值等于该状态的最佳动作a *的 Q 值(因为我们假设最优策略将选择最佳动作),所以V ( s ) = Q ( s , a * ) ,这意味着A ( s , a * ) = 0。在 Dueling DQN 中,模型估计状态的值和每个可能动作的优势。由于最佳动作应该具有 0 的优势,因此模型减去最大预测从所有预测的优势中获得优势。这是一个简单的 Dueling DQN 模型,使用 Functional API 实现:
K = keras.backend
input_states = keras.layers.Input(shape=[4])
hidden1 = keras.layers.Dense(32, activation="elu")(input_states)
hidden2 = keras.layers.Dense(32, activation="elu")(hidden1)
state_values = keras.layers.Dense(1)(hidden2)
raw_advantages = keras.layers.Dense(n_outputs)(hidden2)
advantages = raw_advantages - K.max(raw_advantages, axis=1, keepdims=True)
Q_values = state_values + advantages
model = keras.Model(inputs=[input_states], outputs=[Q_values])这算法的其余部分与之前的相同。事实上,您可以构建一个双重决斗 DQN 并将其与优先体验重放相结合!更一般地说,可以组合许多 RL 技术,正如 DeepMind 在2017 年的一篇论文中所展示的那样。18 _论文的作者将六种不同的技术组合成一个名为Rainbow的代理,它在很大程度上优于最先进的技术。
不幸的是,实现所有这些技术、调试它们、微调它们,当然还有训练模型可能需要大量的工作。因此,与其重新发明轮子,不如重用可扩展且经过良好测试的库,例如 TF-Agents。
TF-Agent 库
这 TF-Agents 库是一个基于 TensorFlow 的强化学习库,由 Google 开发并于 2018 年开源。就像 OpenAI Gym 一样,它提供了许多现成的环境(包括所有 OpenAI Gym 环境的包装器),此外它还支持PyBullet 库(用于 3D 物理模拟)、DeepMind 的 DM Control 库(基于 MuJoCo 的物理引擎)和 Unity 的 ML-Agents 库(模拟许多 3D 环境)。它还实现了许多 RL 算法,包括 REINFORCE、DQN 和 DDQN,以及各种 RL 组件,例如高效的重放缓冲区和指标。它快速、可扩展、易于使用和可定制:您可以创建自己的环境和神经网络,并且几乎可以定制任何组件。在本节中,我们将使用 TF-Agents 训练代理进行游戏Breakout,著名的 Atari 游戏(见图 18-11 19),使用 DQN 算法(如果您愿意,可以轻松切换到另一种算法)。
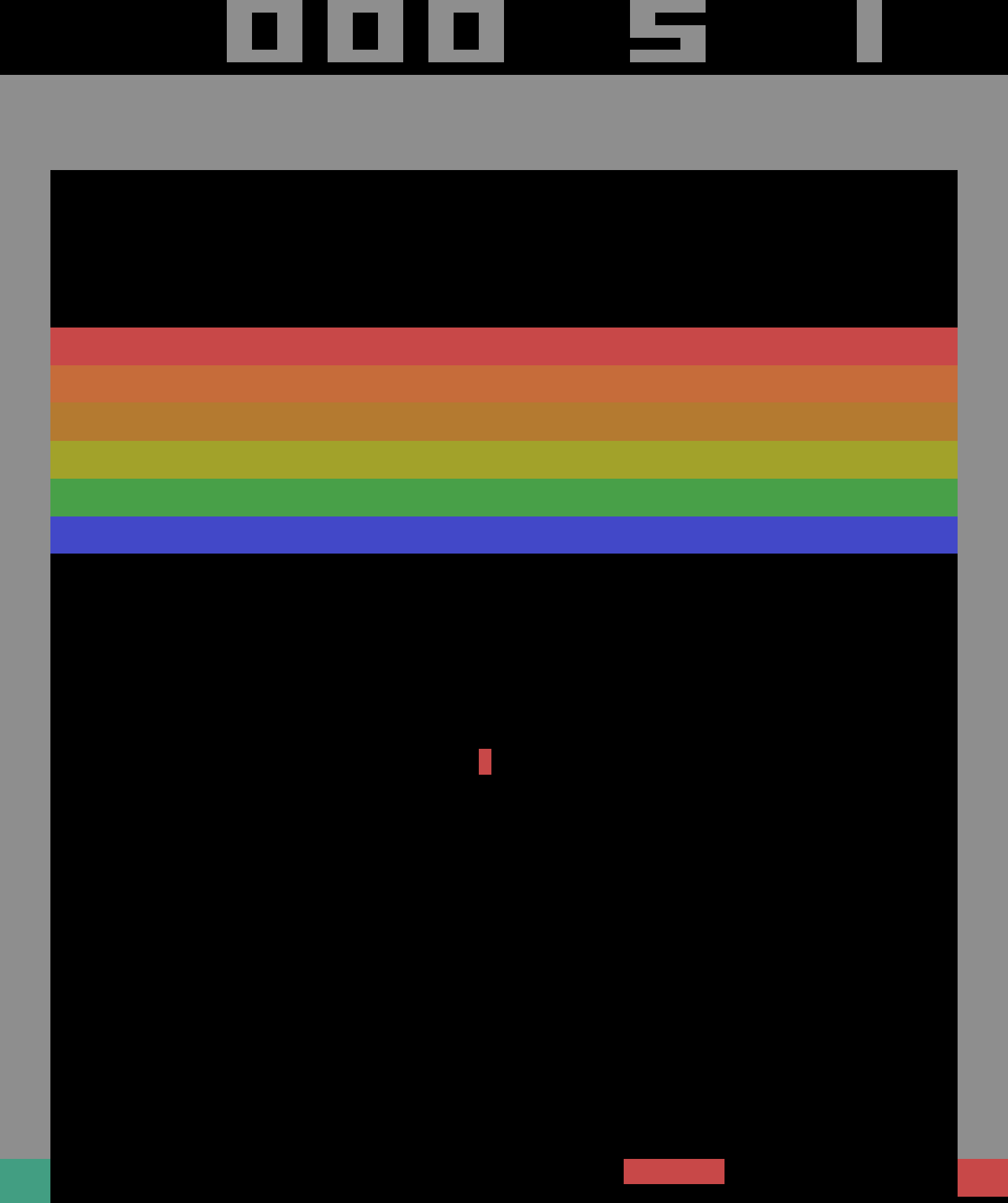
图 18-11。著名的突围游戏
安装 TF 代理
让我们首先安装 TF-Agents。这可以使用 pip 完成(与往常一样,如果您使用的是虚拟环境,请确保先激活它;如果没有,您将需要使用该--user选项,或拥有管理员权限):
$ python3 -m pip install -U tf-agents警告
在撰写本文时,TF-Agents 仍然很新,并且每天都在改进,所以当您阅读本文时,API 可能会发生一些变化——但总体情况应该保持不变,大部分代码也是如此。如果有任何问题,我会相应地更新 Jupyter notebook,所以一定要检查一下。
接下来,让我们创建一个仅包装 OpenAI GGym 的 Breakout 环境的 TF-Agents 环境。为此,您必须首先安装 OpenAI Gym 的 Atari 依赖项:
$ python3 -m pip install -U 'gym[atari]'在其他库中,此命令将安装atari-pyArcade Learning Environment (ALE) 的 Python 接口,这是一个构建在 Atari 2600 模拟器 Stella 之上的框架。
TF-Agents 环境
如果一切顺利,您应该能够导入 TF-Agents 并创建一个 Breakout 环境:
>>> from tf_agents.environments import suite_gym
>>> env = suite_gym.load("Breakout-v4")
>>> env
<tf_agents.environments.wrappers.TimeLimit at 0x10c523c18>这只是 OpenAI Gym 环境的包装,您可以通过gym属性访问它:
>>> env.gym
<gym.envs.atari.atari_env.AtariEnv at 0x24dcab940>TF-Agents 环境与 OpenAI Gym 环境非常相似,但也有一些不同之处。首先,该reset()方法不返回观察值;相反,它返回一个TimeStep包装观察的对象,以及一些额外的信息:
>>> env.reset()
TimeStep(step_type=array(0, dtype=int32),
reward=array(0., dtype=float32),
discount=array(1., dtype=float32),
observation=array([[[0., 0., 0.], [0., 0., 0.],...]]], dtype=float32))该step()方法也返回一个TimeStep对象:
>>> env.step(1) # Fire
TimeStep(step_type=array(1, dtype=int32),
reward=array(0., dtype=float32),
discount=array(1., dtype=float32),
observation=array([[[0., 0., 0.], [0., 0., 0.],...]]], dtype=float32))reward和observation属性是不言自明的,它们与 OpenAI Gym 相同(除了表示reward为 NumPy 数组)。该step_type属性在情节中的第一个时间步等于 0,对于中间时间步等于 1,对于最后一个时间步等于 2。您可以调用时间步的is_last()方法来检查它是否是最后一个。最后,该discount属性指示在此时间步使用的折扣因子。在此示例中,它等于 1,因此根本不会有折扣。discount您可以在加载环境时通过设置参数来定义折扣因子。
笔记
在任何时候,您都可以通过调用其
current_time_step()方法来访问环境的当前时间步长。
环境规格
方便地,一个TF-Agents 环境提供了观察、动作和时间步长的规范,包括它们的形状、数据类型和名称,以及它们的最小值和最大值:
>>> env.observation_spec()
BoundedArraySpec(shape=(210, 160, 3), dtype=dtype('float32'), name=None,
minimum=[[[0. 0. 0.], [0. 0. 0.],...]],
maximum=[[[255., 255., 255.], [255., 255., 255.], ...]])
>>> env.action_spec()
BoundedArraySpec(shape=(), dtype=dtype('int64'), name=None,
minimum=0, maximum=3)
>>> env.time_step_spec()
TimeStep(step_type=ArraySpec(shape=(), dtype=dtype('int32'), name='step_type'),
reward=ArraySpec(shape=(), dtype=dtype('float32'), name='reward'),
discount=BoundedArraySpec(shape=(), ..., minimum=0.0, maximum=1.0),
observation=BoundedArraySpec(shape=(210, 160, 3), ...))如您所见,观察结果只是 Atari 屏幕的屏幕截图,表示为形状为 [210, 160, 3] 的 NumPy 数组。要渲染环境,你可以调用env.render(mode="human"),如果你想以 NumPy 数组的形式取回图像,只需调用env.render(mode="rgb_array")(与 OpenAI Gym 不同,这是默认模式)。
有四个可用的操作。Gym 的 Atari 环境有一个额外的方法,您可以调用它来了解每个操作对应的内容:
>>> env.gym.get_action_meanings()
['NOOP', 'FIRE', 'RIGHT', 'LEFT']小费
规范可以是规范类、嵌套列表或规范字典的实例。如果规范是嵌套的,那么指定的对象必须与规范的嵌套结构相匹配。例如,如果观察规范是
{"sensors": ArraySpec(shape=[2]), "camera": ArraySpec(shape=[100, 100])},那么有效的观察将是{"sensors": np.array([1.5, 3.5]), "camera": np.array(...)}。该tf.nest软件包提供了处理此类嵌套结构(又名nests)的工具。
观测值非常大,因此我们将对它们进行下采样并将它们转换为灰度。这将加快训练并使用更少的 RAM。为此,我们可以使用环境包装器。
环境包装器和 Atari 预处理
TF-代理在包中提供了几个环境包装器tf_agents.environments.wrappers。正如他们的名字所暗示的那样,他们包装了一个环境,将每个调用转发给它,但还添加了一些额外的功能。以下是一些可用的包装器:
ActionClipWrapper
将动作剪辑到动作规范。
ActionDiscretizeWrapper
将连续动作空间量化为离散动作空间。例如,如果原始环境的动作空间是从 –1.0 到 +1.0 的连续范围,但您想使用仅支持离散动作空间的算法,例如 DQN,则可以使用 包装环境discrete_env = ActionDiscretizeWrapper(env, num_actions=5),并且新的discrete_env将有一个离散的动作空间,其中包含五个可能的动作:0、1、2、3、4。这些动作对应于原始环境中的动作 –1.0、–0.5、0.0、0.5 和 1.0。
ActionRepeat
在n步内重复每个动作,同时累积奖励。在许多环境中,这可以显着加快训练速度。
RunStats
记录环境统计信息,例如步数和情节数。
TimeLimit
如果运行时间超过最大步数,则中断环境。
要创建一个包装的环境,您必须创建一个包装器,将包装的环境传递给构造函数。就这样!例如,以下代码将我们的环境包装在一个ActionRepeat包装器中,以便每个操作重复四次:
from tf_agents.environments.wrappers import ActionRepeat
repeating_env = ActionRepeat(env, times=4)OpenAI Gym 在包中有一些自己的环境包装器gym.wrappers。但是,它们旨在包装 Gym 环境,而不是 TF-Agents 环境,因此要使用它们,您必须首先使用 Gym 包装器包装 Gym 环境,然后使用 TF-Agents 包装器包装生成的环境。如果您给它一个 Gym 环境和一个 Gym 包装器列表和/或 TF-Agents 包装器列表,该suite_gym.wrap_env()函数将为您执行此操作。或者,suite_gym.load()如果你给它一些包装器,该函数将创建 Gym 环境并为你包装它。每个包装器都将在没有任何参数的情况下创建,所以如果你想设置一些参数,你必须传递一个lambda. 例如,以下代码创建了一个 Breakout 环境,该环境将在每个情节中运行最多 10,000 步,并且每个动作将重复四次:
from gym.wrappers import TimeLimit
limited_repeating_env = suite_gym.load(
"Breakout-v4",
gym_env_wrappers=[lambda env: TimeLimit(env, max_episode_steps=10000)],
env_wrappers=[lambda env: ActionRepeat(env, times=4)])对于 Atari 环境,在使用它们的大多数论文中都应用了一些标准的预处理步骤,因此 TF-Agents 提供了一个方便的AtariPreprocessing包装器来实现它们。以下是它支持的预处理步骤列表:
灰度和下采样
观测值被转换为灰度和下采样(默认为 84 × 84 像素)。
最大池化
游戏的最后两帧使用 1 × 1 过滤器进行最大池化。这是为了消除某些 Atari 游戏中由于 Atari 2600 可以在每帧中显示的精灵数量有限而出现的闪烁。
跳帧
代理只能看到游戏的每n帧(默认情况下n = 4),并且每帧重复其动作,收集所有奖励。从智能体的角度来看,这有效地加快了游戏速度,并且还加快了训练,因为奖励延迟更少。
结束失去的生命
在某些游戏中,奖励仅基于分数,因此代理不会因失去生命而立即受到惩罚。一种解决方案是在失去生命时立即结束游戏。关于这种策略的实际好处存在一些争论,因此默认情况下它是关闭的。
由于默认的 Atari 环境已经应用了随机跳帧和最大池化,我们需要加载名为"BreakoutNoFrameskip-v4". 此外, Breakout游戏的单帧不足以知道球的方向和速度,这将使智能体很难正常玩游戏(除非它是 RNN 智能体,它在步骤之间保留了一些内部状态)。处理此问题的一种方法是使用环境包装器,该包装器将输出由沿通道维度堆叠的多个帧组成的观察值。这个策略由FrameStack4包装器实现,它返回四帧的堆栈。让我们创建包装好的 Atari 环境!
from tf_agents.environments import suite_atari
from tf_agents.environments.atari_preprocessing import AtariPreprocessing
from tf_agents.environments.atari_wrappers import FrameStack4
max_episode_steps = 27000 # <=> 108k ALE frames since 1 step = 4 frames
environment_name = "BreakoutNoFrameskip-v4"
env = suite_atari.load(
environment_name,
max_episode_steps=max_episode_steps,
gym_env_wrappers=[AtariPreprocessing, FrameStack4])所有这些预处理的结果如图 18-12所示。您可以看到分辨率要低得多,但足以玩游戏。此外,帧是沿着通道维度堆叠的,所以红色代表三步前的帧,绿色是两步前的帧,蓝色是前一帧,紫色是当前帧。20从这一次观察中,代理可以看到球正朝着左下角移动,并且它应该继续将球拍向左移动(就像在前面的步骤中所做的那样)。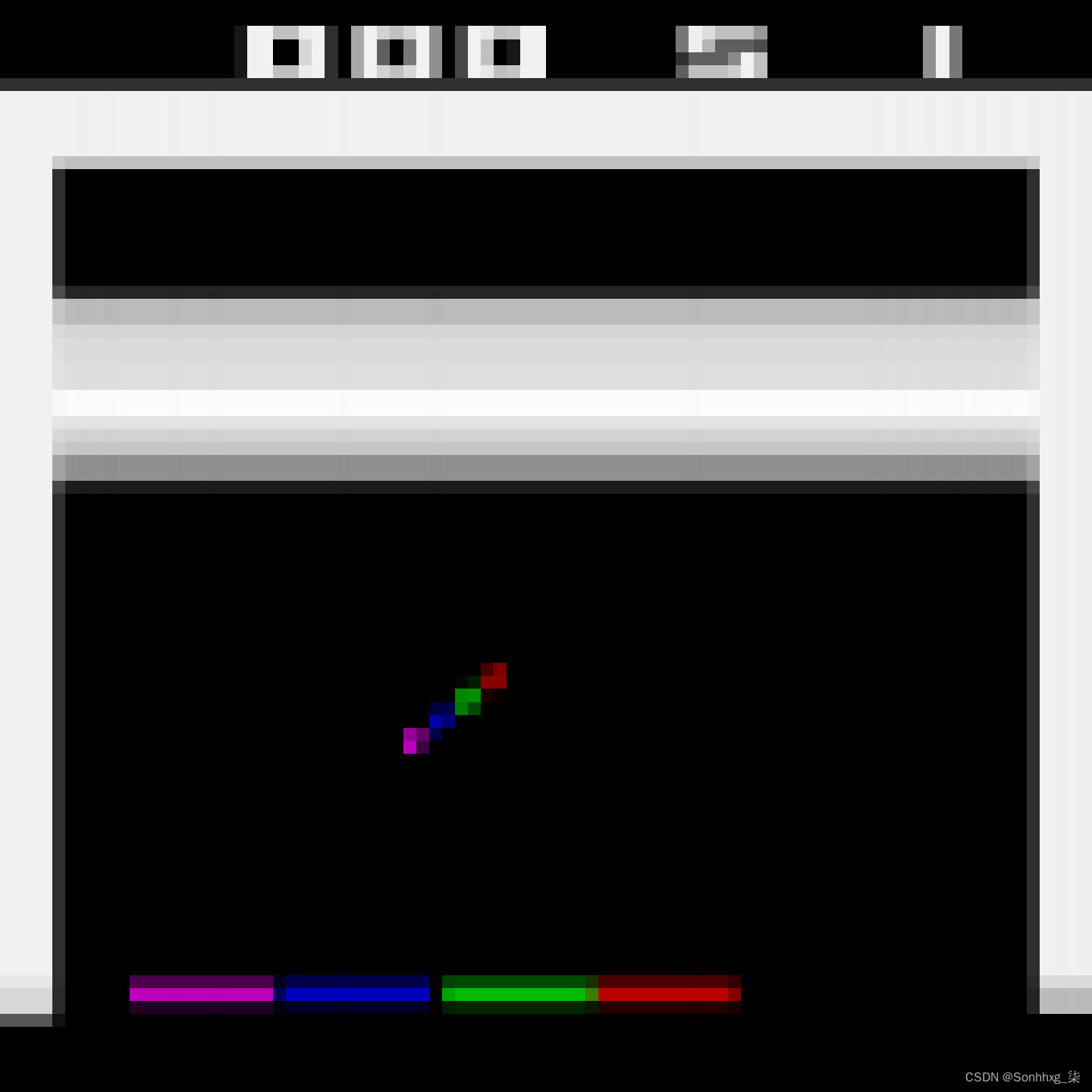
图 18-12。预处理突破观察
最后,我们可以将环境包装在 a 中TFPyEnvironment:
from tf_agents.environments.tf_py_environment import TFPyEnvironment
tf_env = TFPyEnvironment(env)这将使环境可以在 TensorFlow 图内使用(在底层,这个类依赖于tf.py_function(),它允许图调用任意 Python 代码)。由于TFPyEnvironment该类,TF-Agents 支持纯 Python 环境和基于 TensorFlow 的环境。更一般地说,TF-Agents 支持并提供纯 Python 和基于 TensorFlow 的组件(代理、重放缓冲区、指标等)。
现在我们有了一个不错的 Breakout 环境,以及所有适当的预处理和 TensorFlow 支持,我们必须创建 DQN 代理和我们需要训练它的其他组件。让我们看看我们将要构建的系统的架构。
培训架构(Training Architecture)
TF-Agents 培训计划通常分为并行运行的两部分,如图 18-13 所示:在左侧,驱动程序使用收集策略探索环境以选择动作,它收集轨迹(即经验),发送它们到观察者,将它们保存到重放缓冲区;在右侧,代理从重放缓冲区中提取一批轨迹并训练收集策略使用的一些网络。简而言之,左边部分探索环境并收集轨迹,而右边部分学习和更新收集策略。
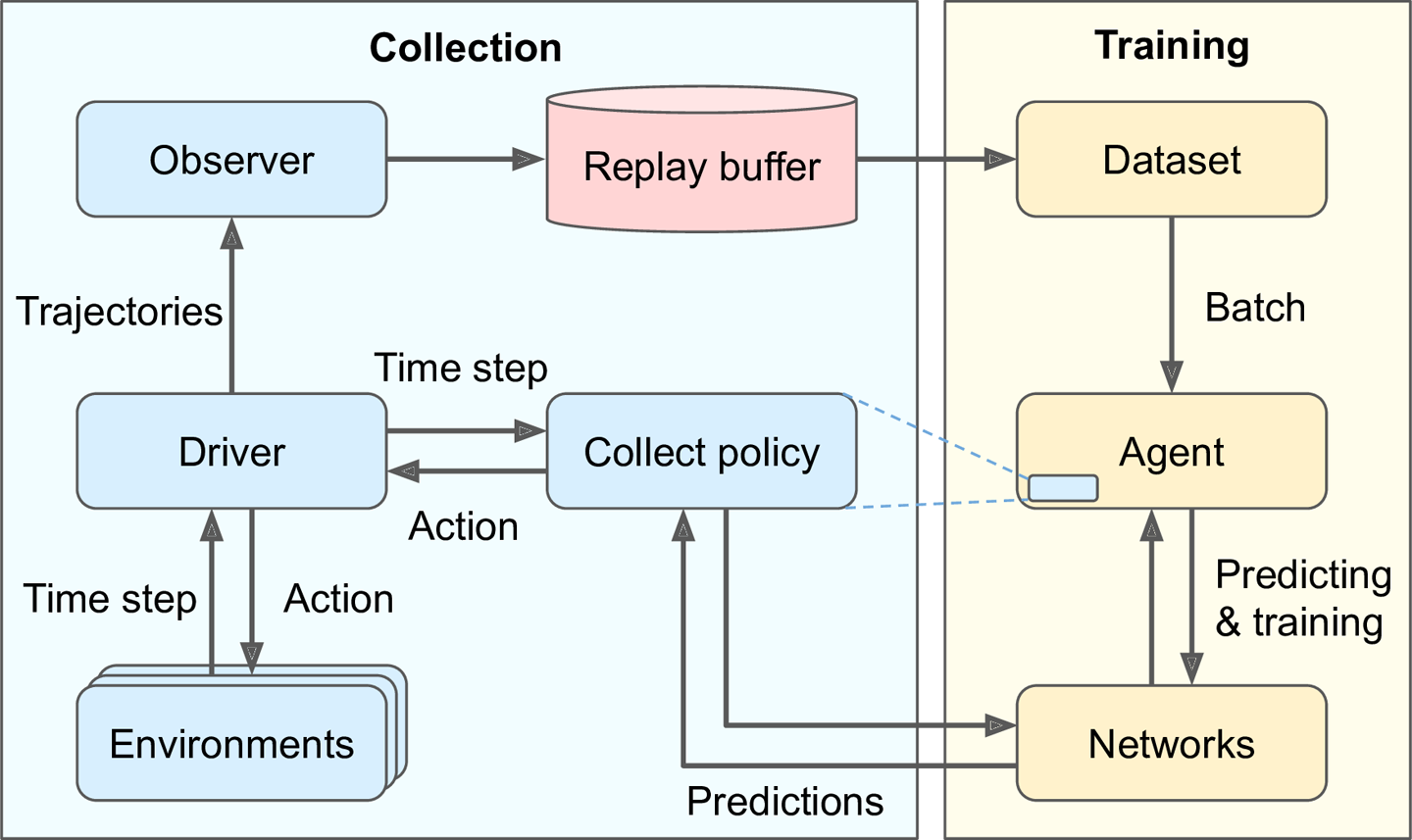
图 18-13。典型的 TF-Agents 训练架构
这个数字引出了几个问题,我将在这里尝试回答:
-
为什么会有多个环境?您通常希望驱动程序并行探索环境的多个副本,而不是探索单个环境,利用所有 CPU 内核的强大功能,保持训练 GPU 繁忙,并为训练算法提供相关性较低的轨迹。
-
什么是一个轨迹?它是从一个时间步到下一个时间步的转换的简明表示,或从时间步n到时间步n + t的一系列连续转换。驱动程序收集的轨迹被传递给观察者,观察者将它们保存在回放缓冲区中,然后由代理对其进行采样并用于训练。
-
为什么我们需要观察者?驱动程序不能直接保存轨迹吗?确实,它可以,但这会降低架构的灵活性。例如,如果您不想使用重放缓冲区怎么办?如果您想将轨迹用于其他用途,例如计算指标,该怎么办?事实上,观察者只是任何以轨迹为参数的函数。您可以使用观察者将轨迹保存到重放缓冲区,或将它们保存到 TFRecord 文件(参见第 13 章),或计算指标,或用于其他任何事情。此外,您可以将多个观察者传递给驱动程序,它会将轨迹广播给所有观察者。
小费
虽然这种架构是最常见的,但你可以随意定制,甚至可以用自己的组件替换一些组件。事实上,除非您正在研究新的 RL 算法,否则您很可能希望为您的任务使用自定义环境。为此,您只需要创建一个自定义类,该类继承自包中的
PyEnvironment类tf_agents.environments.py_environment并覆盖适当的方法,例如action_spec()、observation_spec()、_reset()和_step()(请参阅笔记本的“创建自定义 TF-Agents 环境”部分以获取示例)。
现在我们将创建所有这些组件:首先是 Deep Q-Network,然后是 DQN 代理(它将负责创建收集策略),然后是重放缓冲区和写入它的观察者,然后是一些训练指标,然后驱动程序,最后是数据集。一旦我们准备好所有组件,我们将使用一些初始轨迹填充回放缓冲区,然后我们将运行主训练循环。所以,让我们从创建深度 Q 网络开始。
创建深度 Q 网络
这TF-Agents 库在tf_agents.networks包及其子包中提供了许多网络。我们将使用tf_agents.networks.q_network.QNetwork该类:
from tf_agents.networks.q_network import QNetwork
preprocessing_layer = keras.layers.Lambda(
lambda obs: tf.cast(obs, np.float32) / 255.)
conv_layer_params=[(32, (8, 8), 4), (64, (4, 4), 2), (64, (3, 3), 1)]
fc_layer_params=[512]
q_net = QNetwork(
tf_env.observation_spec(),
tf_env.action_spec(),
preprocessing_layers=preprocessing_layer,
conv_layer_params=conv_layer_params,
fc_layer_params=fc_layer_params)这QNetwork将观察作为输入并为每个动作输出一个 Q 值,因此我们必须为其提供观察和动作的规范。它从一个预处理层开始:一个简单的Lambda将观察结果转换为 32 位浮点数并对其进行归一化的层(值的范围为 0.0 到 1.0)。观察包含无符号字节,它使用的空间比 32 位浮点数少 4 倍,这就是为什么我们没有更早地将观察结果转换为 32 位浮点数的原因;我们想在回放缓冲区中保存 RAM。接下来,网络应用了三个卷积层:第一个有 32 个 8 × 8 过滤器,使用步幅为 4,第二个有 64 个 4×4 过滤器,步幅为 2,第三个有 64 个 3×3 过滤器,步幅为1。最后,它应用一个具有 512 个单元的密集层,然后是一个具有 4 个单元的密集输出层,每个 Q 值一个输出(即每个动作一个)。所有卷积层和除输出层外的所有密集层默认使用 ReLU 激活函数(您可以通过设置activation_fn争论)。输出层不使用任何激活函数。
在底层,aQNetwork由两部分组成:一个处理观察结果的编码网络,然后是一个密集输出层,每个动作输出一个 Q 值。TF-Agent 的EncodingNetwork类实现了在各种代理中发现的神经网络架构(见图 18-14)。
它可能有一个或多个输入。例如,如果每个观察都由一些传感器数据加上来自相机的图像组成,那么您将有两个输入。每个输入可能需要一些预处理步骤,在这种情况下,您可以通过参数指定 Keras 层列表,preprocessing_layers每个输入有一个预处理层,网络会将每一层应用于相应的输入(如果输入需要多层预处理,您可以传递整个模型,因为 Keras 模型始终可以用作层)。如果有两个或更多输入,您还必须通过preprocessing_combiner参数传递一个额外的层,以将预处理层的输出组合成一个输出。
接下来,如果您通过参数指定它们的参数,编码网络将有选择地按顺序应用卷积列表conv_layer_params。这必须是一个由 3 元组(每个卷积层一个)组成的列表,指示过滤器的数量、内核大小和步幅。在这些卷积层之后,如果您设置参数,编码网络将选择性地应用一系列密集层fc_layer_params:它必须是包含每个密集层的神经元数量的列表。dropout_layer_params或者,如果您想在每个密集层之后应用丢弃,您还可以通过参数传递丢弃率列表(每个密集层一个) 。获取此编码网络的QNetwork输出并将其传递给密集输出层(每个动作一个单元)。
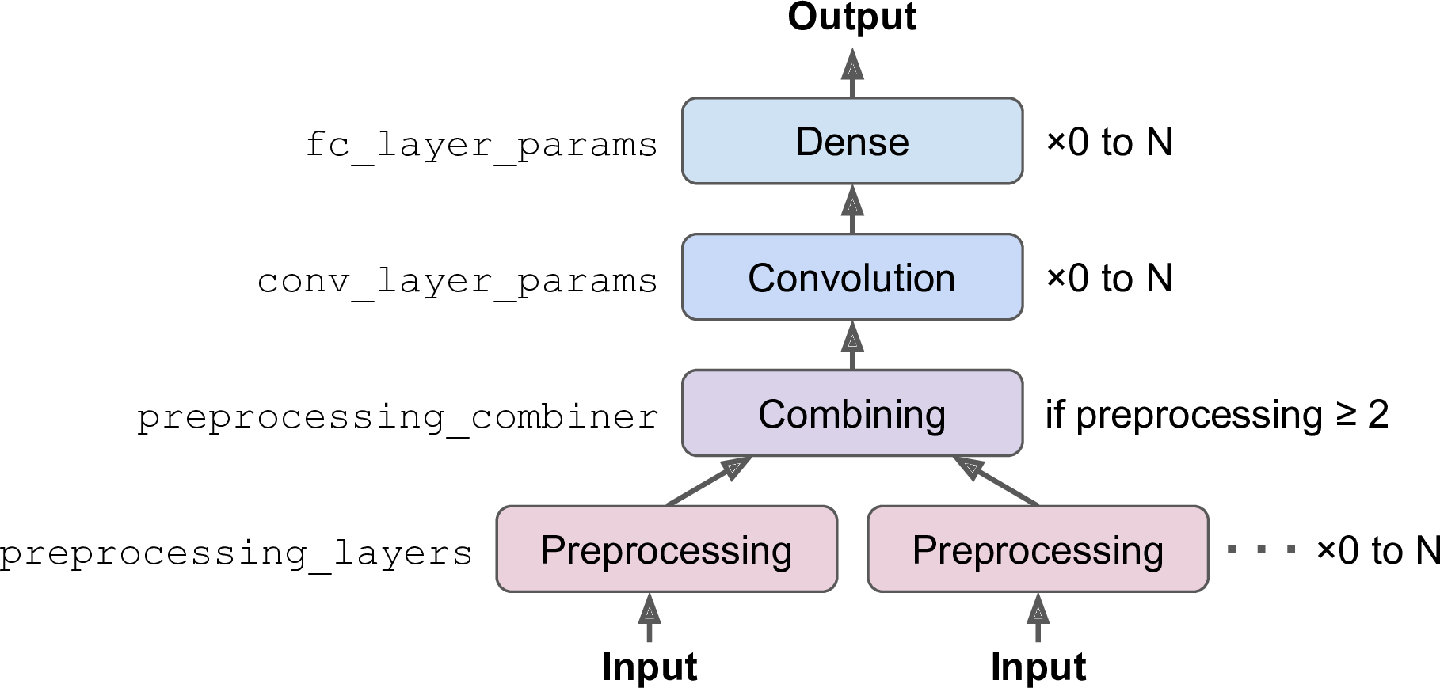
图 18-14。编码网络的架构
笔记
该类
QNetwork足够灵活,可以构建许多不同的架构,但如果您需要额外的灵活性,您始终可以构建自己的网络类:扩展tf_agents.networks.Network该类并像常规自定义 Keras 层一样实现它。该类tf_agents.networks.Network是该类的子keras.layers.Layer类,它添加了某些代理所需的一些功能,例如轻松创建网络的浅表副本的可能性(即,复制网络的架构,但不复制其权重)。例如,DQNAgent使用它来创建在线模型的副本。
既然我们有了 DQN,我们就可以构建 DQN 代理了。
创建 DQN 代理
这TF-Agents 库实现了多种类型的代理,位于tf_agents.agents包及其子包中。我们将使用tf_agents.agents.dqn.dqn_agent.DqnAgent该类:
from tf_agents.agents.dqn.dqn_agent import DqnAgent
train_step = tf.Variable(0)
update_period = 4 # train the model every 4 steps
optimizer = keras.optimizers.RMSprop(lr=2.5e-4, rho=0.95, momentum=0.0,
epsilon=0.00001, centered=True)
epsilon_fn = keras.optimizers.schedules.PolynomialDecay(
initial_learning_rate=1.0, # initial ε
decay_steps=250000 // update_period, # <=> 1,000,000 ALE frames
end_learning_rate=0.01) # final ε
agent = DqnAgent(tf_env.time_step_spec(),
tf_env.action_spec(),
q_network=q_net,
optimizer=optimizer,
target_update_period=2000, # <=> 32,000 ALE frames
td_errors_loss_fn=keras.losses.Huber(reduction="none"),
gamma=0.99, # discount factor
train_step_counter=train_step,
epsilon_greedy=lambda: epsilon_fn(train_step))
agent.initialize()让我们看一下这段代码:
-
我们首先创建一个变量来计算训练步骤的数量。
-
然后我们构建优化器,使用与 2015 DQN 论文中相同的超参数。
-
接下来,我们创建一个
PolynomialDecay对象,它将计算ε -greedy collect 策略的ε值,给定当前的训练步骤(它通常用于衰减学习率,因此参数的名称,但它可以很好地工作衰减任何其他值)。它将在 100 万个 ALE 帧中从 1.0 下降到 0.01(在 2015 年 DQN 论文中使用的值),这对应于 250,000 步,因为我们使用周期为 4 的跳帧。此外,我们将每训练一次代理4 个步骤(即 16 个 ALE 帧),因此ε实际上会在 62,500 个训练步骤中衰减。 -
然后我们构建
DQNAgent,将时间步和动作规范、QNetwork要训练的、优化器、目标模型更新之间的训练步数、要使用的损失函数、折扣因子、train_step变量和返回ε值(它必须不带参数,这就是为什么我们需要一个 lambda 来传递train_step)。请注意,损失函数必须为每个实例返回一个错误,而不是平均错误,这就是我们设置
reduction="none". -
最后,我们初始化代理。
接下来,让我们构建重放缓冲区和将写入它的观察者。
创建重播缓冲区和相应的观察者
这TF-Agents 库在tf_agents.replay_buffers包中提供了各种重放缓冲区实现。有些纯粹是用 Python 编写的(它们的模块名称以 开头py_),而另一些则是基于 TensorFlow 编写的(它们的模块名称以 开头tf_)。我们将使用包TFUniformReplayBuffer中的类tf_agents.replay_buffers.tf_uniform_replay_buffer。它提供了具有统一采样的重放缓冲区的高性能实现:21
from tf_agents.replay_buffers import tf_uniform_replay_buffer
replay_buffer = tf_uniform_replay_buffer.TFUniformReplayBuffer(
data_spec=agent.collect_data_spec,
batch_size=tf_env.batch_size,
max_length=1000000)让我们看一下这些论点:
data_spec
将保存在重放缓冲区中的数据的规范。DQN 代理知道收集到的数据会是什么样子,它通过其collect_data_spec属性使数据规范可用,所以这就是我们给回放缓冲区的内容。
batch_size
将在每一步添加的轨迹数。在我们的例子中,它将是一个,因为驱动程序每一步只执行一个动作并收集一个轨迹。如果环境是批处理环境,即在每一步执行一批操作并返回一批观察结果的环境,那么驱动程序必须在每一步保存一批轨迹。由于我们使用的是 TensorFlow 重放缓冲区,它需要知道它将处理的批次的大小(以构建计算图)。批处理环境的一个示例是ParallelPyEnvironment(来自tf_agents.environments.parallel_py_environment包):它在不同的进程中并行运行多个环境(它们可以不同,只要它们具有相同的动作和观察规范),并且在每个步骤中它需要一批动作并在环境中执行它们(每个动作一个动作环境),然后它返回所有结果观察。
max_length
重播缓冲区的最大大小。我们创建了一个可以存储一百万条轨迹的大型回放缓冲区(如 2015 年 DQN 论文中所做的那样)。这将需要大量 RAM。
小费
当我们存储两个连续的轨迹时,它们包含两个连续的观察值,每个观察值有四个帧(因为我们使用了
FrameStack4包装器),不幸的是,第二个观察中的四个帧中有三个是多余的(它们已经存在于第一个观察中)。换句话说,我们使用的 RAM 大约是所需的四倍。为避免这种情况,您可以改用包中的 aPyHashedReplayBuffer:tf_agents.replay_buffers.py_hashed_replay_buffer它沿观察的最后一个轴对存储轨迹中的数据进行重复数据删除。
现在我们可以创建将轨迹写入回放缓冲区的观察者。观察者只是一个接受轨迹参数的函数(或可调用对象),因此我们可以直接使用add_batch()方法(绑定到replay_buffer对象)作为观察者:
replay_buffer_observer=replay_buffer.add_batch如果你想创建自己的观察者,你可以编写任何带trajectory参数的函数。如果它必须有一个状态,你可以编写一个带有__call__(self, trajectory)方法的类。例如,这里有一个简单的观察者,每次调用它都会增加一个计数器(除非轨迹表示两个片段之间的边界,这不计为一个步骤),每增加 100 次,它就会显示最多给定总数(回车确保显示的计数器保持在同一行)\r:end=""
class ShowProgress:
def __init__(self, total):
self.counter = 0
self.total = total
def __call__(self, trajectory):
if not trajectory.is_boundary():
self.counter += 1
if self.counter % 100 == 0:
print("\r{}/{}".format(self.counter, self.total), end="")现在让我们创建一些训练指标。
创建训练指标
TF-代理在包中实现了几个 RL 指标tf_agents.metrics,一些纯粹在 Python 中,一些基于 TensorFlow。让我们创建其中的一些来计算剧集数、采取的步数,以及最重要的是每集的平均回报和平均剧集长度:
from tf_agents.metrics import tf_metrics
train_metrics = [
tf_metrics.NumberOfEpisodes(),
tf_metrics.EnvironmentSteps(),
tf_metrics.AverageReturnMetric(),
tf_metrics.AverageEpisodeLengthMetric(),
]笔记
result()在任何时候,您都可以通过调用其方法(例如,train_metrics[0].result())来获取这些指标中的每一个的值。或者,您可以通过调用记录所有指标log_metrics(train_metrics)(此函数位于tf_agents.eval.metric_utils包中):
>>> from tf_agents.eval.metric_utils import log_metrics
>>> import logging
>>> logging.get_logger().set_level(logging.INFO)
>>> log_metrics(train_metrics)
[...]
NumberOfEpisodes = 0
EnvironmentSteps = 0
AverageReturn = 0.0
AverageEpisodeLength = 0.0接下来,让我们创建收集驱动程序。
创建收集驱动程序
作为我们在图 18-13中探讨过,驱动程序是使用给定策略探索环境、收集经验并将其广播给一些观察者的对象。在每一步,都会发生以下事情:
-
然后驱动程序将操作传递给环境,环境返回下一个时间步。
-
最后,驱动程序创建一个轨迹对象来表示此转换并将其广播给所有观察者。
一些策略,例如 RNN 策略,是有状态的:它们根据给定的时间步长和它们自己的内部状态来选择一个动作。有状态的策略在操作步骤中返回它们自己的状态,以及选择的操作。然后驱动程序将在下一个时间步将此状态传递回策略。此外,驱动程序将策略状态保存到轨迹(在policy_info现场),因此它最终会进入重放缓冲区。这在训练有状态策略时至关重要:当代理对轨迹进行采样时,它必须将策略的状态设置为采样时间步时所处的状态。
此外,如前所述,环境可能是批处理环境,在这种情况下驱动程序将一个批处理时间步传递给策略(即,一个时间步对象包含一批观察、一批步长类型、一批奖励和一批折扣,所有四个批次的大小相同)。驱动程序还传递了一批先前的策略状态。然后,该策略返回一个包含一批操作和一批策略状态的批处理操作步骤。最后,司机创建一个批处理轨迹(即,一个轨迹包含一批步骤类型、一批观察、一批动作、一批奖励,更一般地说,每个轨迹属性都有一个批次,所有批次的大小相同)。
有两个主要的驱动程序类:DynamicStepDriver和DynamicEpisodeDriver. 第一个收集给定数量的步骤的经验,而第二个收集给定数量的情节的经验。我们希望为每个训练迭代收集四个步骤的经验(如 2015 DQN 论文中所做的那样),所以让我们创建一个DynamicStepDriver:
from tf_agents.drivers.dynamic_step_driver import DynamicStepDriver
collect_driver = DynamicStepDriver(
tf_env,
agent.collect_policy,
observers=[replay_buffer_observer] + training_metrics,
num_steps=update_period) # collect 4 steps for each training iteration我们给它一个可以玩的环境、代理的收集策略、一个观察者列表(包括回放缓冲区观察者和训练指标),最后是要运行的步数(在本例中为四个)。我们现在可以通过调用它的run()方法来运行它,但最好使用纯随机策略收集的经验来预热回放缓冲区。为此,我们可以使用RandomTFPolicy该类并创建第二个驱动程序,该驱动程序将运行此策略 20,000 步(相当于 80,000 个模拟器帧,如 2015 年 DQN 论文中所做的那样)。我们可以使用我们的ShowProgress观察者来显示进度:
from tf_agents.policies.random_tf_policy import RandomTFPolicy
initial_collect_policy = RandomTFPolicy(tf_env.time_step_spec(),
tf_env.action_spec())
init_driver = DynamicStepDriver(
tf_env,
initial_collect_policy,
observers=[replay_buffer.add_batch, ShowProgress(20000)],
num_steps=20000) # <=> 80,000 ALE frames
final_time_step, final_policy_state = init_driver.run()我们几乎准备好运行训练循环了!我们只需要最后一个组件:数据集。
创建数据集
至从回放缓冲区中采样一批轨迹,调用它的get_next()方法。这将返回一批轨迹加上一个BufferInfo包含样本标识符及其采样概率的对象(这可能对某些算法有用,例如 PER)。例如,以下代码将对一小批两条轨迹(子集)进行采样,每条轨迹包含三个连续的步骤。这些子集如图 18-15所示(每行包含一个集的三个连续步骤):
>>> trajectories, buffer_info = replay_buffer.get_next(
... sample_batch_size=2, num_steps=3)
...
>>> trajectories._fields
('step_type', 'observation', 'action', 'policy_info',
'next_step_type', 'reward', 'discount')
>>> trajectories.observation.shape
TensorShape([2, 3, 84, 84, 4])
>>> trajectories.step_type.numpy()
array([[1, 1, 1],
[1, 1, 1]], dtype=int32)该trajectories对象是一个命名元组,有七个字段。每个字段包含一个张量,其前两个维度是 2 和 3(因为有两个轨迹,每个轨迹有三个步骤)。这就解释了为什么observation场的形状是 [2, 3, 84, 84, 4]:那是两条轨迹,每条有 3 个步长,每步的观测值是 84 × 84 × 4。同样,step_type张量的形状是 [ 2, 3]:在这个例子中,两个轨迹在一个情节的中间都包含三个连续的步骤(类型 1、1、1)。在第二个轨迹中,你几乎看不到第一次观察左下角的球,在接下来的两次观察中它就消失了,所以代理即将失去生命,但情节不会立即结束,因为它还有还剩几条命。
图 18-15。两条轨迹,每条轨迹包含三个连续的步骤
每个轨迹都是一系列连续时间步骤和动作步骤的简明表示,旨在避免冗余。怎么会这样?好吧,如图 18-16 所示,转移n由时间步n、动作步n和时间步n + 1 组成,而转移n + 1 由时间步n + 1、动作步n +组成1,时间步长n + 2。如果我们只是将这两个转换直接存储在重放缓冲区中,时间步长n + 1 将被复制。为了避免这种重复,第n个轨迹步骤仅包括来自时间步骤n的类型和观察(不包括其奖励和折扣),并且它不包含来自时间步骤n + 1 的观察结果(但是,它确实包含下一个时间步骤类型的副本;这就是仅重复)。
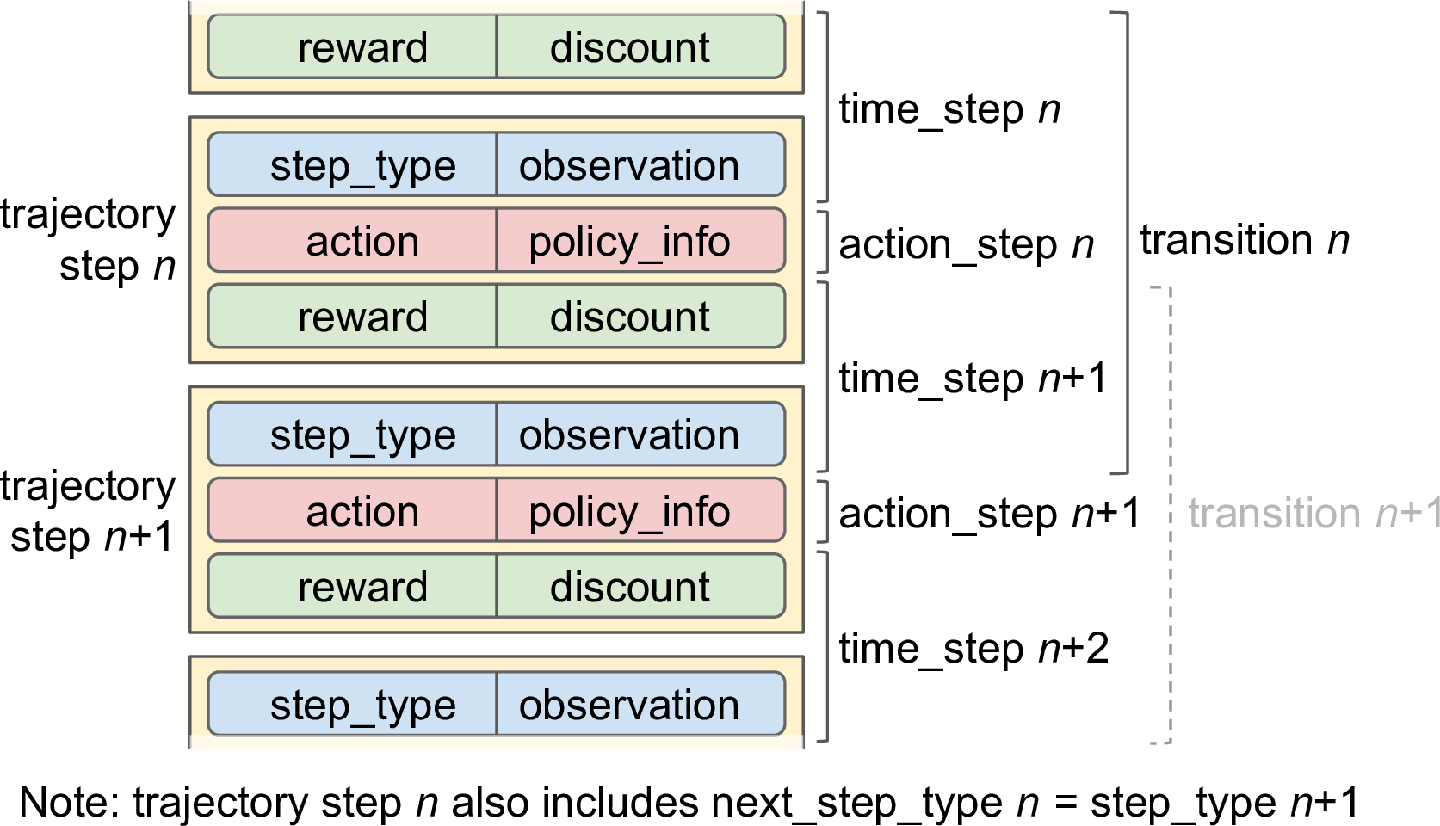
图 18-16。轨迹、转换、时间步长和动作步长
因此,如果您有一批轨迹,其中每个轨迹有t + 1 步(从时间步n到时间步n + t),那么它包含从时间步n到时间步n + t的所有数据,除了奖励和时间步n的折扣(但它包含时间步n + t + 1 的奖励和折扣)。这表示t个转换(n到n + 1,n + 1 到n + 2,...,n + t – 1 到n+ t )。
模块中的to_transition()函数tf_agents.trajectories.trajectory将批处理轨迹转换为包含批处理time_step、批处理action_step和批处理的列表next_time_step。请注意,第二个维度是 2 而不是 3,因为在t + 1 个时间步之间有t个转换(如果您有点困惑,请不要担心;您会掌握它的窍门):
>>> from tf_agents.trajectories.trajectory import to_transition
>>> time_steps, action_steps, next_time_steps = to_transition(trajectories)
>>> time_steps.observation.shape
TensorShape([2, 2, 84, 84, 4]) # 3 time steps = 2 transitions笔记
对于我们的主训练循环,get_next()我们将使用tf.data.Dataset. 通过这种方式,我们可以受益于数据 API 的强大功能(例如,并行性和预取)。为此,我们调用重播缓冲区的as_dataset()方法:
dataset = replay_buffer.as_dataset(
sample_batch_size=64,
num_steps=2,
num_parallel_calls=3).prefetch(3)我们将在每个训练步骤(如 2015 年 DQN 论文中)对 64 个轨迹进行批量采样,每个有 2 个步骤(即 2 个步骤 = 1 个完整转换,包括下一步的观察)。该数据集将并行处理三个元素,并预取三个批次。
笔记
对于策略梯度(Policy Gradients)等策略上的算法,每个经验都应该采样一次,从训练中使用,然后丢弃。在这种情况下,您仍然可以使用重播缓冲区,但不是使用 a
Dataset,而是在每次训练迭代时调用重播缓冲区的gather_all()方法以获取包含迄今为止记录的所有轨迹的张量,然后使用它们执行训练步骤,最后通过调用其clear()方法清除重播缓冲区。
现在我们已经准备好所有组件,我们准备好训练模型了!
创建训练循环
至加快训练速度,我们将主要函数转换为 TensorFlow 函数。为此,我们将使用tf_agents.utils.common.function()wraps 的函数tf.function()以及一些额外的实验选项:
from tf_agents.utils.common import function
collect_driver.run = function(collect_driver.run)
agent.train = function(agent.train)让我们创建一个小函数来运行主训练循环n_iterations:
def train_agent(n_iterations):
time_step = None
policy_state = agent.collect_policy.get_initial_state(tf_env.batch_size)
iterator = iter(dataset)
for iteration in range(n_iterations):
time_step, policy_state = collect_driver.run(time_step, policy_state)
trajectories, buffer_info = next(iterator)
train_loss = agent.train(trajectories)
print("\r{} loss:{:.5f}".format(
iteration, train_loss.loss.numpy()), end="")
if iteration % 1000 == 0:
log_metrics(train_metrics)该函数首先询问收集策略的初始状态(给定环境批量大小,在本例中为 1)。由于策略是无状态的,这将返回一个空元组(所以我们可以写policy_state = ())。接下来,我们在数据集上创建一个迭代器,然后运行训练循环。在每次迭代中,我们调用驱动程序的run()方法,将当前时间步(最初None)和当前策略状态传递给它。它将运行收集策略并收集四个步骤的经验(如我们之前配置的),将收集的轨迹广播到重放缓冲区和指标。接下来,我们从数据集中抽取一批轨迹,并将其传递给代理的train()方法。它返回一个train_loss对象可能因代理类型而异。接下来,我们显示迭代次数和训练损失,每 1000 次迭代我们记录所有指标。现在你可以调用train_agent()一些迭代次数,然后看到代理逐渐学会玩Breakout!
train_agent(10000000)这个将需要大量的计算能力和耐心(可能需要数小时甚至数天,具体取决于您的硬件),而且您可能需要使用不同的随机种子多次运行该算法才能获得良好的结果,但一旦完成后,代理将是超人(至少在Breakout时)。你也可以尝试在其他 Atari 游戏上训练这个 DQN 代理:它可以在大多数动作游戏中达到超人的技能,但它在故事情节较长的游戏中表现不佳。22
一些流行的强化学习算法概述
Actor-Critic 算法
一个将策略梯度与深度 Q 网络相结合的 RL 算法系列。Actor-Critic 代理包含两个神经网络:一个策略网络和一个 DQN。DQN 通过学习代理的经验进行正常训练。与常规 PG 相比,策略网络的学习方式不同(而且速度更快):代理(actor)不是通过经历多个情节来估计每个动作的价值,然后对每个动作的未来折扣奖励求和,最后对它们进行归一化,而是依赖于由 DQN (critic) 估计的动作值。这有点像运动员(代理)在教练(DQN)的帮助下学习。
异步优势 Actor-Critic 23 (A3C)
一个DeepMind 研究人员在 2016 年引入了重要的 Actor-Critic 变体,其中多个代理并行学习,探索环境的不同副本。每隔一段时间,但异步(因此得名),每个代理将一些权重更新推送到主网络,然后从该网络中提取最新的权重。因此,每个智能体都有助于改进主网络,并从其他智能体所学的知识中受益。此外,DQN 不是估计 Q 值,而是估计每个动作的优势(因此名称中的第二个 A),这可以稳定训练。
优势演员-评论家(A2C)
一个消除异步性的 A3C 算法的变体。所有模型更新都是同步的,因此梯度更新是在更大的批次上执行的,这使得模型能够更好地利用 GPU 的能力。
一个Tuomas Haarnoja 和其他加州大学伯克利分校的研究人员在 2018 年提出了 Actor-Critic 变体。它不仅学习奖励,还学习最大化其行为的熵。换句话说,它试图尽可能地不可预测,同时仍然获得尽可能多的奖励。这鼓励代理探索环境,从而加快训练速度,并在 DQN 产生不完美估计时减少重复执行相同动作的可能性。该算法展示了惊人的样本效率(与之前所有学习非常缓慢的算法相反)。SAC 在 TF-Agents 中可用。
一个基于 A2C 的算法,对损失函数进行裁剪以避免过大的权重更新(这通常会导致训练不稳定)。PPO 是John Schulman 和其他 OpenAI 研究人员对先前Trust Region Policy Optimization 26 (TRPO) 算法的简化。OpenAI 于 2019 年 4 月推出了基于 PPO 算法的名为 OpenAI Five 的 AI,该算法在多人游戏Dota 2中击败了世界冠军。PPO 也可用于 TF-Agents。
一个RL 中反复出现的问题是奖励的稀疏性,这使得学习非常缓慢且效率低下。Deepak Pathak 和其他加州大学伯克利分校的研究人员提出了一种令人兴奋的方法来解决这个问题:为什么不忽略奖励,而只是让代理对探索环境非常好奇呢?因此,奖励成为代理所固有的,而不是来自环境。同样,激发孩子的好奇心比单纯奖励孩子取得好成绩更有可能产生好成绩。这是如何运作的?代理不断尝试预测其行为的结果,并寻找结果与其预测不匹配的情况。换句话说,它想要感到惊讶。如果结果是可预测的(无聊的),它就会去别处。然而,如果结果是不可预测的,但代理注意到它无法控制它,它也会在一段时间后感到无聊。出于好奇,作者成功地在许多电子游戏中训练了一个代理:即使代理不会因为输球而受到惩罚,但游戏重新开始,这很无聊,所以它学会了避免它。
本章涵盖了许多主题:策略梯度、马尔可夫链、马尔可夫决策过程、Q-Learning、Approximate Q-Learning 和 Deep Q-Learning 及其主要变体(固定 Q-Value 目标、Double DQN、Dueling DQN 和优先的经验回放)。我们讨论了如何使用 TF-Agents 来大规模训练代理,最后我们快速浏览了一些其他流行的算法。强化学习是一个巨大而令人兴奋的领域,每天都有新的想法和算法涌现,所以我希望这一章能激发你的好奇心:有一个完整的世界等着你去探索!
练习
-
你如何定义强化学习?它与常规的有监督或无监督学习有何不同?
-
你能想到本章没有提到的三种可能的强化学习应用吗?对于他们每个人来说,环境是什么?代理是什么?有哪些可能的行动?有什么奖励?
-
什么是折扣系数?如果修改折扣因子,最优策略会改变吗?
-
您如何衡量强化学习代理的性能?
-
什么是信用分配问题?什么时候发生?你怎么能减轻它?
-
使用重放缓冲区有什么意义?
-
什么是离策略 RL 算法?
-
使用策略梯度来解决 OpenAI Gym 的 LunarLander-v2 环境。您将需要安装 Box2D 依赖项 (
python3 -m pip install -U gym[box2d])。 -
使用 TF-Agents 训练一个可以使用任何可用算法在 SpaceInvaders-v4 上达到超人水平的代理。
-
如果你有大约 100 美元的闲钱,你可以购买一个 Raspberry Pi 3 加上一些便宜的机器人组件,在 Pi 上安装 TensorFlow,然后尽情享受吧!例如,查看 Lukas Biewald 的这篇有趣的帖子,或查看 GoPiGo 或 BrickPi。从简单的目标开始,例如让机器人转身寻找最亮的角度(如果它有光传感器)或最近的物体(如果它有声纳传感器),然后朝那个方向移动。然后你可以开始使用深度学习:例如,如果机器人有一个摄像头,你可以尝试实现一个对象检测算法,以便它检测到人和向他们移动。您还可以尝试使用 RL 让代理自己学习如何使用电机来实现该目标。玩得开心!
附录 A中提供了这些练习的解决方案。
1有关更多详细信息,请务必查看 Richard Sutton 和 Andrew Barto 关于 RL 的书,强化学习:简介 (麻省理工学院出版社)。
2Volodymyr Mnih 等人,“使用深度强化学习玩 Atari”,arXiv 预印本 arXiv:1312.5602 (2013)。
3Volodymyr Mnih 等人,“通过深度强化学习进行人类水平控制”,Nature 518 (2015): 529–533。
4在https://homl.info/dqn3上查看 DeepMind 系统学习玩Space Invaders、Breakout和其他视频游戏的视频。
5图片 (a) 来自 NASA(公共领域)。(b) 是Ms. Pac-Man游戏的截图,版权 Atari(在本章中合理使用)。图片 (c) 和 (d) 转载自维基百科。(c) 由用户 Stevertigo 创建并在Creative Commons BY-SA 2.0下发布。(d) 属于公有领域。(e) 转载自Pixabay,在Creative Commons CC0下发布。
6通常最好给表现不佳的人一点生存机会,以保留“基因库”中的一些多样性。
7如果有单亲,这称为无性繁殖。有两个(或更多)父母,称为有性生殖。后代的基因组(在这种情况下是一组策略参数)是由其父母基因组的一部分随机组成的。
8用于强化学习的遗传算法的一个有趣示例是增强拓扑的神经进化(NEAT) 算法。
9这称为梯度上升。它就像梯度下降,但方向相反:最大化而不是最小化。
10OpenAI 是一家人工智能研究公司,部分资金来自埃隆·马斯克。其既定目标是促进和开发有益于人类(而不是消灭人类)的友好人工智能。
11Ronald J. Williams,“用于连接主义强化学习的简单统计梯度跟随算法”,机器学习8 (1992):229–256。
12理查德贝尔曼,“马尔可夫决策过程” ,数学与力学杂志6,第 6 期。5 (1957): 679–684。
13Alex Irpan在2018 年发表的一篇很棒的文章很好地阐述了 RL 的最大困难和局限。
14Hado van Hasselt 等人,“Double Q-Learning 的深度强化学习” ,第 30 届 AAAI 人工智能会议论文集(2015 年):2094-2100。
15Tom Schaul 等人,“Prioritized Experience Replay”,arXiv 预印本 arXiv:1511.05952 (2015)。
16也可能只是奖励是嘈杂的,在这种情况下,有更好的方法来估计体验的重要性(请参阅论文中的一些示例)。
17Ziyu Wang 等人,“Dueling Network Architectures for Deep Reinforcement Learning”,arXiv 预印本 arXiv:1511.06581 (2015)。
18Matteo Hessel 等人,“Rainbow:结合深度强化学习的改进”,arXiv 预印本 arXiv:1710.02298

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容







所有评论(0)