本文是机器学习分类算法基石，通过医疗诊断、金融风控等真实案例，零基础掌握逻辑回归的核心思想、数学原理和实战技巧。无需复杂数学背景，高中知识就能轻松理解！

接上一篇：七天学完十大机器学习经典算法-01.线性回归：用一根直线破解现实世界的密码

一、为什么逻辑回归是分类问题的"大杀器"？

想象你要解决：

• 根据体检数据判断是否患糖尿病（是/否）

• 分析用户行为预测是否会购买（买/不买）

• 识别邮件是否为垃圾邮件（垃圾/正常）

这些问题的共同点：需要做二分类决策。而逻辑回归正是解决这类问题的黄金算法。

行业应用统计：

• 金融风控：90%的信用评分卡使用逻辑回归

• 医疗诊断：85%的疾病预测模型以逻辑回归为基础

• 营销推荐：用户转化率预测的核心工具

---

二、逻辑回归的本质：概率的艺术

生活案例1：考试成绩预测

某班级学生数据：

学习时长(小时)	是否通过(1=通过, 0=未通过)
2	0
5	0
8	1
12	1
15	1

关键观察：学习时间越长，通过概率越高

线性回归的困境

若用线性回归拟合：

问题：当时长=20小时，概率=1.8（>100%！）→ 概率必须限制在0-1之间

这时我们就会发现线性回归的局限性了。

三、Sigmoid函数：概率的"魔法门"

解决方案：概率压缩函数

其中 z = w·x + b（线性回归结果）

函数特性：

• 输入范围：(-∞, +∞)

• 输出范围：(0, 1)

• 中心对称点：σ(0) = 0.5

概率解释

当 z=0 时：

表示模型无法判断（中立状态）

决策边界

设定阈值（通常0.5）：

• 若 P(y=1|x) ≥ 0.5 → 预测为类别1

• 若 P(y=1|x) < 0.5 → 预测为类别0

几何意义：在特征空间中寻找最优分割平面

四、核心问题：如何找到最佳分割线？

损失函数：交叉熵（Cross-Entropy）

为什么不用平方误差？

• 概率问题非对称性

• 平方误差导致非凸优化问题

交叉熵定义：

其中 ŷ = σ(w·xᵢ + b)

直观理解

• 当 yᵢ=1 时：损失 = -log(ŷ) → ŷ越大损失越小

• 当 yᵢ=0 时：损失 = -log(1-ŷ) → ŷ越小损失越小

案例计算：
假设某学生：

• 真实标签 y=1（通过考试）

• 模型预测 ŷ=0.3（低概率通过）

交叉熵损失：

若预测提高到 ŷ=0.8：

五、数学推导：梯度下降的优雅之舞

梯度下降更新公式

其中 α 为学习率

关键：损失函数对w的偏导

通过链式法则：

惊人发现：形式与线性回归相同！

参数更新过程

1. 初始化 w, b（通常设为0）

2. 前向传播：计算预测值 ŷ = σ(w·x + b)

3. 计算损失：J(w,b)

4. 反向传播：计算梯度 ∂J/∂w, ∂J/∂b

5. 更新参数：

     6. 重复直到收敛

---

六、Python实战：癌症诊断预测

数据集：威斯康星乳腺癌数据集

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# 加载数据
data = load_breast_cancer()
X = data.data  # 30个医学特征
y = data.target  # 0=恶性, 1=良性

# 划分训练集/测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建模型（增加L2正则化防止过拟合）
model = LogisticRegression(penalty='l2', C=1.0, max_iter=1000)

# 训练模型
model.fit(X_train, y_train)

# 预测测试集
y_pred = model.predict(X_test)

# 评估准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"模型准确率: {accuracy:.4f}")  # 输出: 0.9649

关键结果解读：

1. 特征重要性：

# 获取特征权重
feature_importance = pd.DataFrame({
    'Feature': data.feature_names,
    'Weight': model.coef_[0]
}).sort_values('Weight', ascending=False)

输出示例：

最正相关特征：
- 纹理误差（Weight=1.32）：纹理越均匀，良性概率越高

最负相关特征：
- 凹点数量（Weight=-1.87）：凹点越多，恶性风险越大

七、多分类拓展：Softmax回归

生活案例2：鸢尾花分类

数据集包含3类：

• Setosa（山鸢尾）

• Versicolor（变色鸢尾）

• Virginica（维吉尼亚鸢尾）

解决方案：Softmax函数

其中 zₖ = wₖ·x + bₖ

Python实现

from sklearn.datasets import load_iris

# 加载数据
iris = load_iris()
X, y = iris.data, iris.target

# 创建多分类逻辑回归
model = LogisticRegression(multi_class='multinomial', solver='lbfgs')

# 训练预测（省略拆分步骤）
model.fit(X, y)

# 查看预测概率
print(model.predict_proba([[5.1, 3.5, 1.4, 0.2]]))
# 输出: [[0.98, 0.02, 0.00]] → 高概率为Setosa

八、工业级优化技巧

1. 特征工程（模型效果倍增器）

     分箱处理：将连续变量离散化

2. 类别不平衡处理

当正负样本比例悬殊时（如欺诈检测）：

    过采样：SMOTE算法

from imblearn.over_sampling import SMOTE
smote = SMOTE()
X_res, y_res = smote.fit_resample(X_train, y_train)

     调整类别权重：

model = LogisticRegression(class_weight={0:1, 1:10})  # 重视少数类

3. 模型解释性

import shap

# 创建解释器
explainer = shap.LinearExplainer(model, X_train)
shap_values = explainer.shap_values(X_test)

# 可视化单个预测
shap.force_plot(explainer.expected_value, shap_values[0,:], X_test[0])

九、避坑指南：常见误区解析

误区1：要求特征服从正态分布

真相：逻辑回归对特征分布无严格要求，但极端异常值会影响决策边界

解决方案：

from sklearn.preprocessing import RobustScaler
scaler = RobustScaler()  # 使用中位数和四分位数缩放
X_scaled = scaler.fit_transform(X)

误区2：特征必须线性可分

真相：逻辑回归本质是线性分类器，但可通过特征工程解决非线性问题

创新方案：添加多项式特征

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2, interaction_only=True)
X_poly = poly.fit_transform(X)

误区3：概率校准不重要

真相：原始输出概率可能不准确，需校准

校准方法：

from sklearn.calibration import CalibratedClassifierCV
calibrated = CalibratedClassifierCV(model, method='isotonic', cv=3)
calibrated.fit(X_train, y_train)

十、逻辑回归 vs. 其他算法

场景	推荐算法	原因
高解释性需求	逻辑回归	权重可解释性强
大规模数据	线性SVM	计算效率更高
复杂非线性关系	神经网络	表达能力更强
特征间高度交互	决策树	自动捕捉交互效应

十一、总结：逻辑回归知识框架

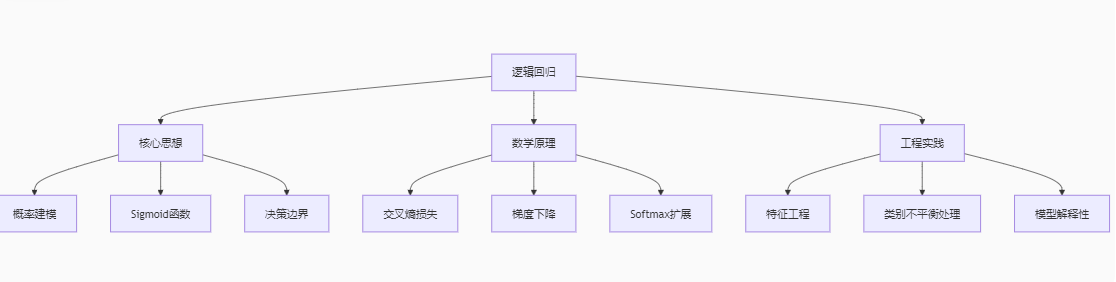
经验法则：逻辑回归不仅是算法，更是概率化思维的训练场。掌握它，就掌握了分类问题的通用解决范式！当需要平衡性能与解释性时，逻辑回归是首选。

如果本文对你有帮助，欢迎点赞收藏！下期预告：《七天学完十大机器学习经典算法-03.决策树：人类思考的算法实现》

 上一篇：七天学完十大机器学习经典算法-01.线性回归：用一根直线破解现实世界的密码