卷积是一种数学运算，核心操作是对两个函数进行平移、相乘后累加。

1. 一维连续卷积公式：

   • 输入：信号函数 ( f(x) ) 和卷积核 ( k(x) )。
   • 步骤：变换变量→翻转→平移→相乘→积分（求乘积曲线下的面积）。

2. 卷积性质：

   • 交换律：( f * k = k * f )
   • 结合律：( (f * g) * k = f * (g * k) )
   • 分配律：( f * (g + k) = f * g + f * k )

3. 离散卷积：

   • 计算机处理离散信号，公式类似但用求和代替积分：

应用：广泛用于音频处理等信号处理领域，连续卷积理论为离散计算提供基础。

一维卷积计算过程

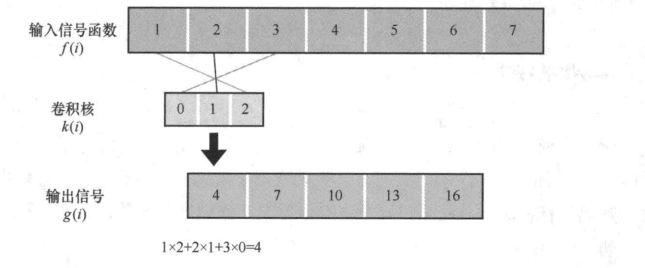
假设输入信号长度为m,卷积核大小为n,可以很容易得到输出信号
的长度为m-n+1。但这是不是意味着对一个输入信号反复卷积，它的输出长度将会越来越小？

实际上，这种情况确实可能存在。因此，为了防止这种情况出现，通常会对输入信号进行
零填充(zero-padding)操作。

对于输入，会在“1”的左边和“7”的右边各添加数字“0”，如此一来输入信号的长度便增加了2，因此对应的输出信号长度也随之增加。

零填充操作让输出信号和输入信号的长度能够保持一致，更有甚者，如果对图中输入信号的左右两边各添加两个“0”，输出信号的长度则大于输入信号的长度。一般来说，在输入信号一边零填充的
个数要小于卷积核的大小。这是因为当0的个数超过或等于卷积核的长度时，卷积所得的结果为
相当于对输出信号也进行了零填充操作，这没有意义。

现在动手编写一维卷积函数并且用数组表示离散函数并对输入信号进行零填充,零填充个数为卷积核大小-1，设置s=1，即步长为1，最终得到的输出信号为m+n-1,可以自己算算

代码

import matplotlib.pyplot as plt
# 一维卷积
class conv_id():
    def __init__(self,a,b):
        # 输入法信号
        self.a = a
        # 卷积核
        self.b = b
        # 输入信号的坐标
        self.ax= [i for i in range(len(a))]
        # 卷积核的坐标
        self.bx = [i for i in range(len(b))]
    def conv(self):
        # 对输入信号a和卷积核b进行数学上的卷积操作
        c = []
        # c[k] = Σ (a[i - j] * b[j]) 就是一维卷积的公式
        for i in range(len(self.a) + len(self.b) - 1):
            s = 0
            for j in range(len(self.b)):
                if i - j >= 0 and i - j < len(self.a):
                    s += self.a[i - j] * self.b[j]
            c.append(s)
        return c
    def plot(self):
            a, b, ax, bx = self.a, self.b, self.ax, self.bx
            c = self.conv()
            cx = [i for i in range(len(c))]
            # 设置画布 1行3列
            plt.figure(figsize=(12, 4))
            # 输入信号
            plt.subplot(1, 3, 1)
            plt.title('Input')
            plt.bar(ax, a, color='lightcoral', width=0.4)
            plt.plot(ax, a, color='red')
            # 卷积核
            plt.subplot(1, 3, 2)
            plt.title('Kernel')
            plt.bar(bx, b, color='lightgreen', width=0.4)
            plt.plot(bx, b, color='green')
            # 输出信号
            plt.subplot(1, 3, 3)
            plt.title('Output')
            plt.bar(cx, c, color='lightseagreen', width=0.4)
            plt.plot(cx, c, color='teal')
            plt.tight_layout()
            plt.show()

# 使用不同卷积核对三角波信号进行卷积
# 观察不同的卷积核的卷积效果
# 定义输入信号和卷积核
a=[0,1,2,3,2,1,0]
# 冲击函数
k=[0,0,1,0,0]
cov= conv_id(a,k)
# 计算卷积并绘图
cov.plot()

输出结果

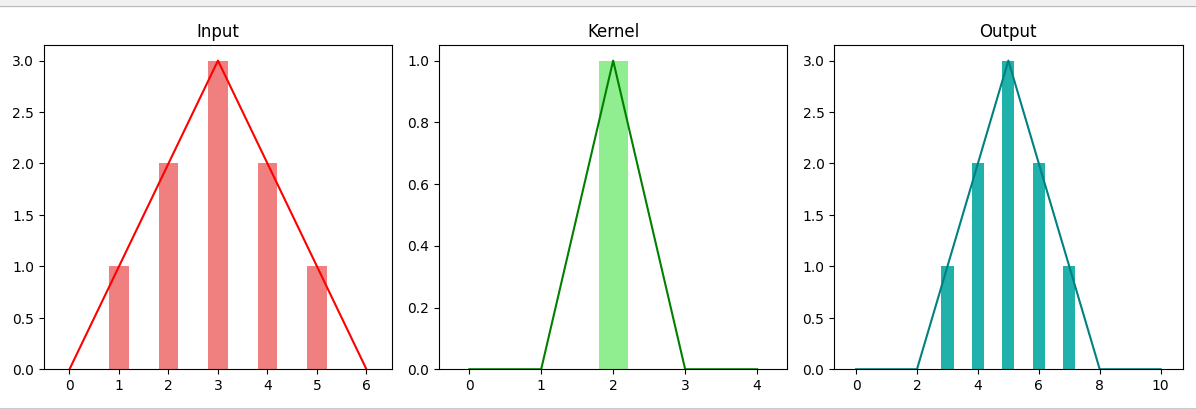当所用的卷积核是一个单位冲激信号(“面积”等于1，即只在一个位置出现的窄脉冲)时，
输入信号在卷积之后并没有发生变化。这是卷积的一个重要性质。

现在更换新的卷积核

# 冲击函数
k=[1,1,1,1,1]

得到结果

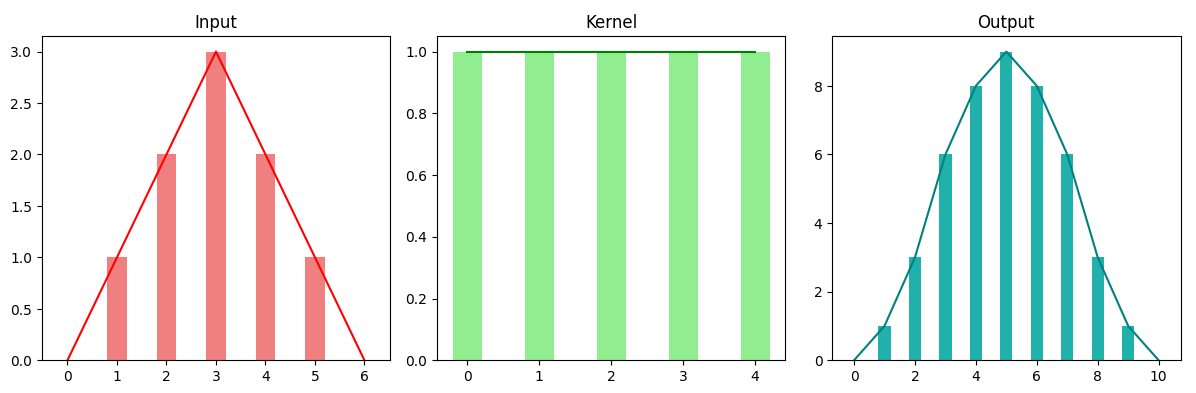
可以看到，用一个方波信号对一个三角波信号进行卷积，其效果是将三角波变得平滑了。