分类器的不确定度估计

scikit-learn 的另一个有用之处就是分类器能给出预测的不确定度估计。我们不仅关心预测点的被分类情况，还关心这个预测的置信度，这个在医学上是很严肃的问题呢。scikit-learn 中有两个函数可以获取不确定度估计，decision_function 和 predict_proba 。

from sklearn.model_selection import train_test_split

from sklearn.ensemble import GradientBoostingClassifier

from sklearn.datasets import make_circles

X, y = make_circles(noise=0.25, factor=0.5, random_state=1)

y_named = np.array(["blue", "red"])[y]

# 所有数组的划分方式都是一致的

X_train, X_test, y_train_named, y_test_named, y_train, y_test = \

train_test_split(X, y_named, y, random_state=0)

gbrt = GradientBoostingClassifier(random_state=0)

gbrt.fit(X_train, y_train_named)

1.决策函数

对于二分类问题，decision_function 返回值的形状是 (n_samples, )，为每个样本都返回一个浮点数。

print("X_test.shape:{}".format(X_test.shape))

print("Decision function shape:{}".format(

gbrt.decision_function(X_test).shape))

对于类别1来说，(25, ) 这个值表示模型对该数据点为“正”的置信度。正值表示对正类的偏好，负值表示对“反类”的偏好。

print("Decision function:\n{}".format(gbrt.decision_function(X_test)[:6]))

我们可以通过仅查看决策函数的正负号来再现预测值。

print("Thresholded decision function:\n{}".

format(gbrt.decision_function(X_test) > 0))

print("Prediction:\n{}".format(gbrt.predict(X_test)))

对于二分类问题，反 始终是classes_属性的第一个元素，正 是第二个。如果要完全再现 predict 的输出，需要利用 classes_ 的属性。

# 将布尔值True/False转换成0和1

greater_zero = (gbrt.decision_function(X_test) > 0).astype(int)

# 利用0和1作为classes_的索引

pred = gbrt.classes_[greater_zero]

# pred与的gbrt.predict输出完全相同

print("pred is equal to predictions: {}".format(np.all(pred == gbrt.predict(X_test))))

decision_function 可以在任意范围取值，取决于数据与模型参数。

decision_function = gbrt.decision_function(X_test)

print("Decision function minimum:{:.2f} maximum:{:.2f}".format(

np.min(decision_function), np.max(decision_function)))

由于可以任意缩放，decision_function 的输出往往很难解释。

fig, axes =plt.subplots(1, 2, figsize=(13, 5))

mglearn.tools.plot_2d_separator(gbrt, X, ax=axes[0], alpha=.4,

fill=True, cm=mglearn.cm2)

scores_image = mglearn.tools.plot_2d_scores(gbrt, X,

ax=axes[1], alpha=.4, cm=mglearn.ReBl)

for ax in axes:

# 画出训练点和测试点

mglearn.discrete_scatter(X_test[:, 0], X_test[:, 1],

y_test, markers='^', ax=ax)

mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1],

y_train, markers='o', ax=ax)

ax.set_xlabel("Feature 0")

ax.set_ylabel("Feature 1")

cbar = plt.colorbar(scores_image, ax=axes.tolist())

axes[0].legend(["Test class 0", "Test class 1",

"Train class 0", "Train class 1"], ncol=4, loc=(.1, 1.1))

plt.show()

​

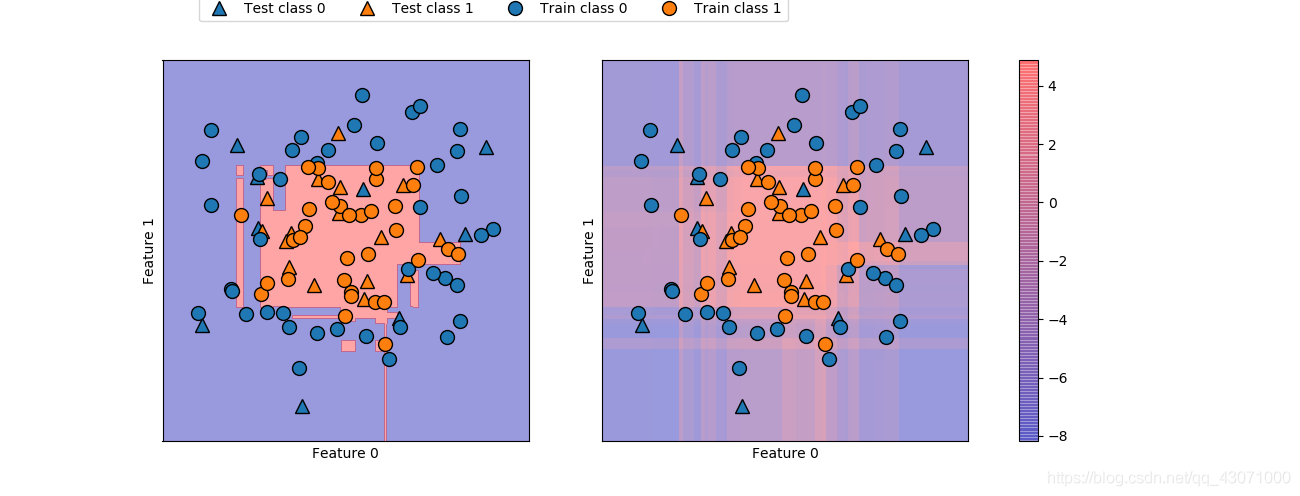
即给出预测结果，又给出分类器的置信程度，这样给出信息量更大。但在上面的图像中，很难分辨出两个类别之间的边界呢？？？喵喵喵，说实话这玩意在分类嘛?正态分布？WTF?小生不才，看不懂= =

2.预测概率

predict_proba 的输出是每个类别的概率，通常比 decision_function 的输出更易理解。对于二分类问题，它的形状始终是 (n_samples, 2)

print("Shape of probabilities: {}".format(gbrt.predict_proba(X_test).shape))

因为两个类别，故两列，分别描述其概率，两个类别元素，即每一行之和始终为1。

# 显示predict_proba的前几个元素

print("Predicted probabilities:\n{}".format(gbrt.predict_proba(X_test[:6])))

可以看到，分类器对大部分点的置信程度都是相对较高的。

不确定度大小实际上反映了数据依赖于模型和参数的不确定度。过拟合更强的模型可能做出置信程度更高的预测，即使可能是错的。

复杂度越低的模型通常对预测的不确定度越大

，如果模型中给出的不确定度符合实际情况，那么这个模型被称为

校正

(calibrated) 模型。在校正模型中，如果预测又70%的确定度，那么她在70%的情况下正确。

fig, axes =plt.subplots(1, 2, figsize=(13, 5))

mglearn.tools.plot_2d_separator(gbrt, X, ax=axes[0], alpha=.4,

fill=True, cm=mglearn.cm2)

scores_image = mglearn.tools.plot_2d_scores(gbrt, X, ax=axes[1], alpha=.5,

cm=mglearn.ReBl, function='predict_proba')

for ax in axes:

# 画出训练点和测试点

mglearn.discrete_scatter(X_test[:, 0], X_test[:, 1],

y_test, markers='^', ax=ax)

mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1],

y_train, markers='o', ax=ax)

ax.set_xlabel("Feature 0")

ax.set_ylabel("Feature 1")

cbar = plt.colorbar(scores_image, ax=axes.tolist())

axes[0].legend(["Test class 0", "Test class 1",

"Train class 0", "Train class 1"], ncol=4, loc=(.1, 1.1))

plt.show()

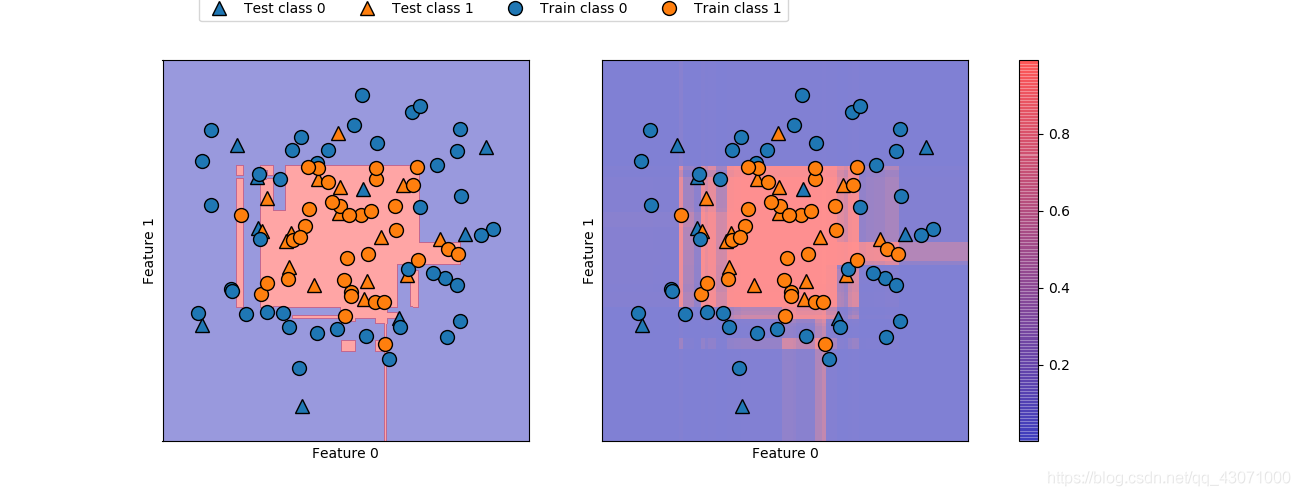
这张图边界更加明确。

3.多分类问题的不确定度

接下来尝试三分类问题。

from sklearn.datasets import load_iris

iris = load_iris()

X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=42)

gbrt = GradientBoostingClassifier(learning_rate=0.01, random_state=0)

gbrt.fit(X_train, y_train)

print("Decision function shape: {}".format(gbrt.decision_function(X_test).shape))

# 显示决策函数的前几个元素

print("Decixion function:\n {}".format(gbrt.decision_function(X_test)[:6, :]))

通常每列为每个类别的 “确定度分数” ，有点类似所属类别的可能性概率？

print("Argma of decision function:\n{}".format(

np.argmax(gbrt.decision_function(X_test), axis=1)))

print("Prediction:\n{}".format(gbrt.predict(X_test)))

print("Predicted probabilities:\n{}".format(gbrt.predict_proba(X_test)[:6]))

# 显示每行的和都是1

print("Sums: {}".format(gbrt.predict_proba(X_test)[:6].sum(axis=1)))

总之，prediict_proba 和 decision_function 的形状始终相同，都是(n_samples, n_classes)。如果有 n_classes 列，我们可以通过计算每一列的 argmax 来再现预测结果。但如果类别是字符串或者整数，但不是从0开始的连续整数的话，一定要小心。如果想要对比 predict 的结果与 prediict_proba 或 decision_function 的结果，一定要用分类器的classes_属性来获取真实的属性名称。

from sklearn.linear_model import LogisticRegression

logreg = LogisticRegression()

# 用Iris数据集的类别名称来表示每一个目标值

named_target = iris.target_names[y_train]

logreg.fit(X_train, named_target)

print("unique classes in training data: {]".format(logreg.classes_))

print("predictions: {}".format(logreg.predict(X_test)[:10]))

argmax_dec_func = np.argmax(logreg.decision_function(X_test), axis=1)

print("argmax of decision function: {}".format(argmax_dec_func[:10]))

print("argmax combined with classes_: {}".format(

logreg.classes_[argmax_dec_func][:10]))