前文:深度强化学习 # Deep-Q-Network利用神经网络对Q value function作近似表示。局限性在于其只适用于action有限的情况（神经网络输出层的节点数显然不能是无限的）。
在前文有提到过NN的两种结构，如果是输入State和action来得到Q呢？这里输出只有一个。是不是可以解决连续情况？答案是否定的。（因为我们还需要对所有的action求一个max(Q），虽然此时NN可以build，但是计算max（Q)时的循环次数无限次，导致max（Q）的计算不可行，且这种做法效率极度低下。
那么我们考虑第三种出路：神经网络输入状态直接输出动作，这就是策略梯度的思想了。

Policy Gradients：不通过分析奖励值, 直接输出行为的方法。对比起以值为基础的方法, Policy Gradients 直接输出动作的最大好处就是, 它能在一个连续区间内挑选动作, 而基于值的, 比如 Q-learning只能适用于action数量有限的情况。Policy Gradients可以结合神经网络。
强化学习里面无标签，DQN因为是基于时序差分学习有Q现实和Q估计的差距所以可以作为loss function，但是PG没有Q，所以Policy Gradients没有误差，那要怎么进行神经网络的误差反向传递呢？（因此还是需要充分利用reward的信息）

Policy Gradients的核心思想： 观测的信息通过神经网络分析, 选出了左边的行为, 我们直接进行反向传递, 使之下次被选的可能性增加, 但是奖惩信息却告诉我们, 这次的行为是不好的, 那我们的动作可能性增加的幅度随之被减低. 假如这次的观测信息让神经网络选择了右边的行为, 右边的行为随之想要进行反向传递, 使右边的行为下次被多选一点, 这时, 奖惩信息也来了, 告诉我们这是好行为, 那我们就在这次反向传递的时候加大力度（好，请加大力度！~）。这样就能靠奖励来左右我们的神经网络反向传递。即loss function是 − R θ ˉ -\bar{R_{\theta}} −Rθ​ˉ​

补充解释一下：为什么policy gradient可以在连续区间选择动作？这里看来动作不是还是离散的吗？而且还是概率选择离散动作。
我们考虑一下：一个连续区间的数值，是否可以通过区间端点和一个比例得到？（定比分点）
所以在输出的概率值（连续值）的基础上乘以一个系数就可以实现获得连续值的输出。


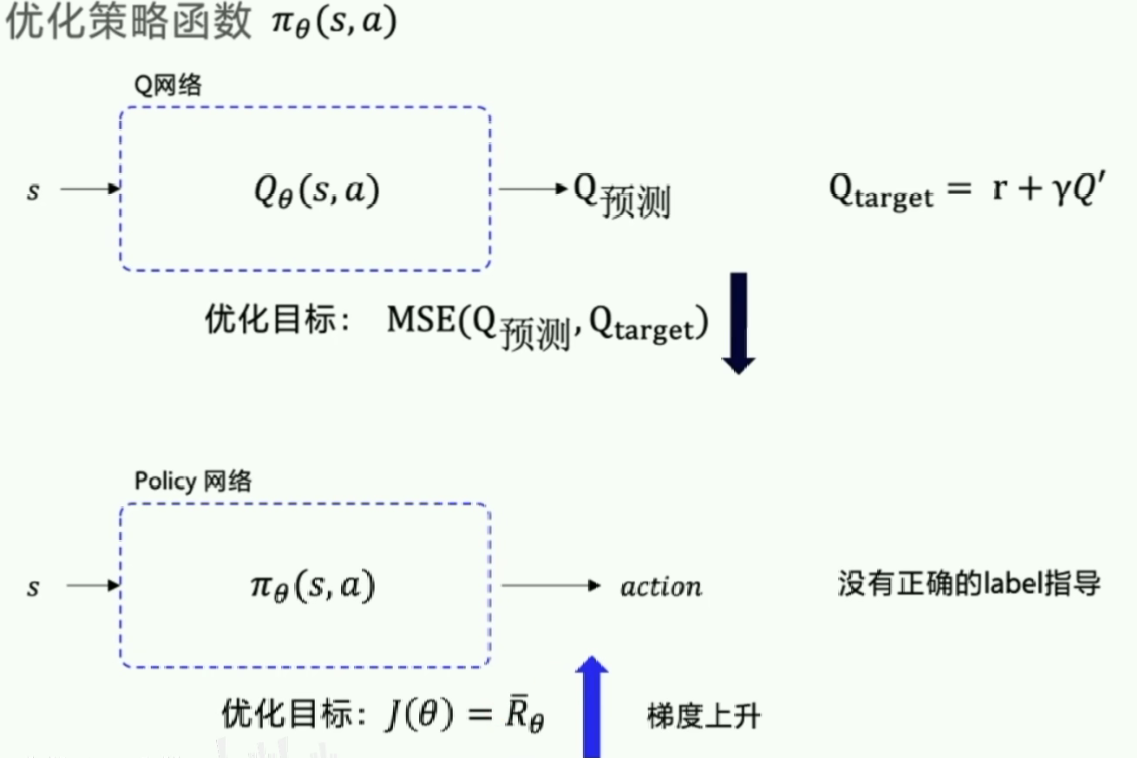
Policy Gradients要输出的不是action对应的value而是action，这样就跳过了 value 这个阶段。最大的一个优势是: 输出的这个 action 可以是一个连续的值, 之前我们说到的 value-based 方法输出的都是不连续的值。


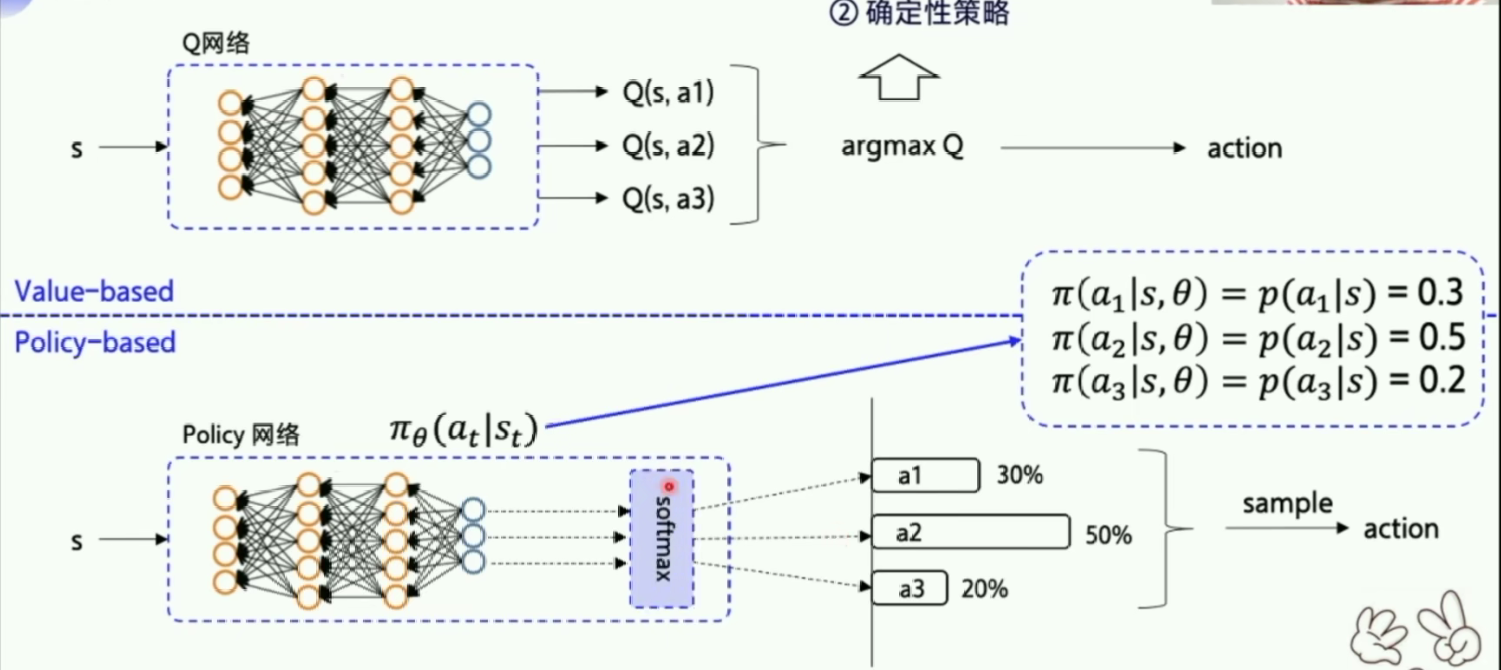
输出概率通过softmax归一化。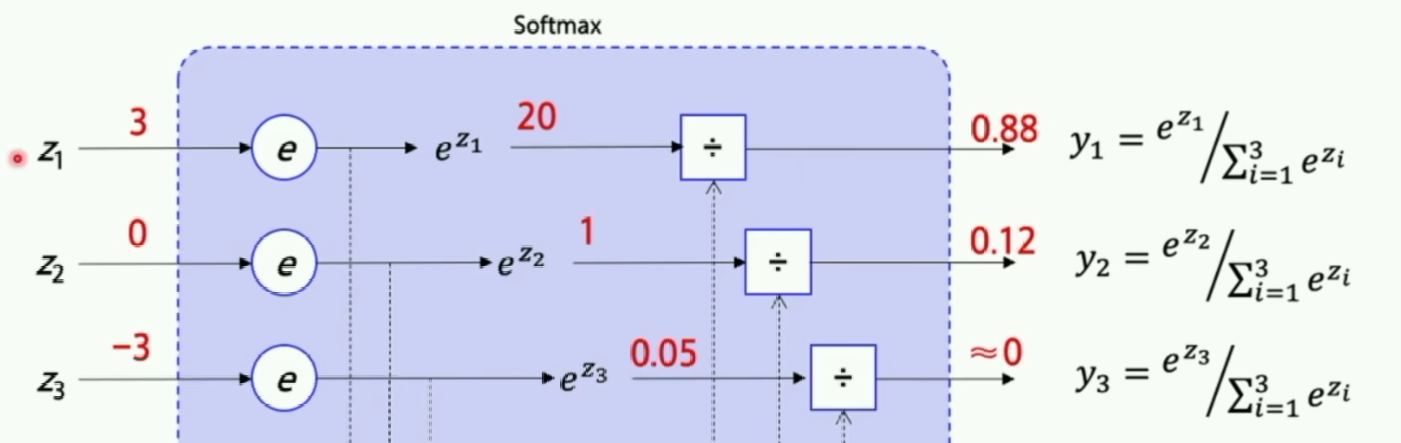

在PG中很多问题是分幕式(Episode)的。优化目标是让每个episode的总reward都尽可能大。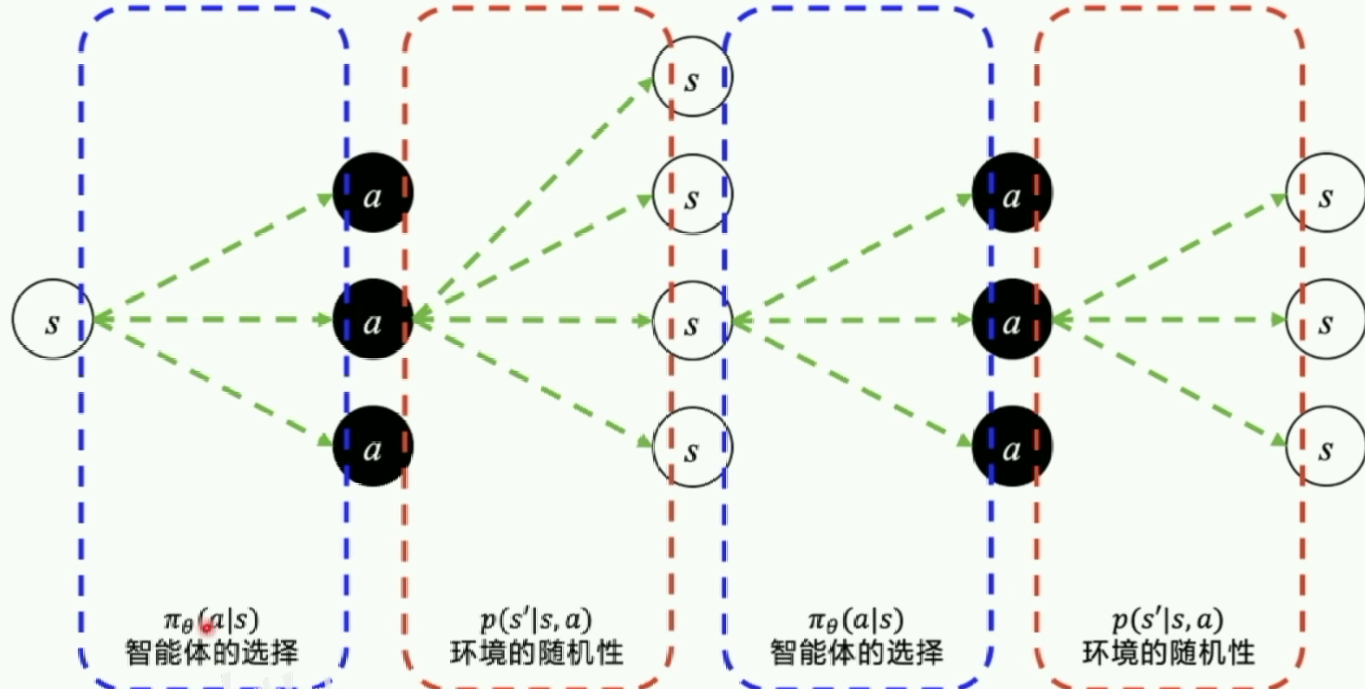

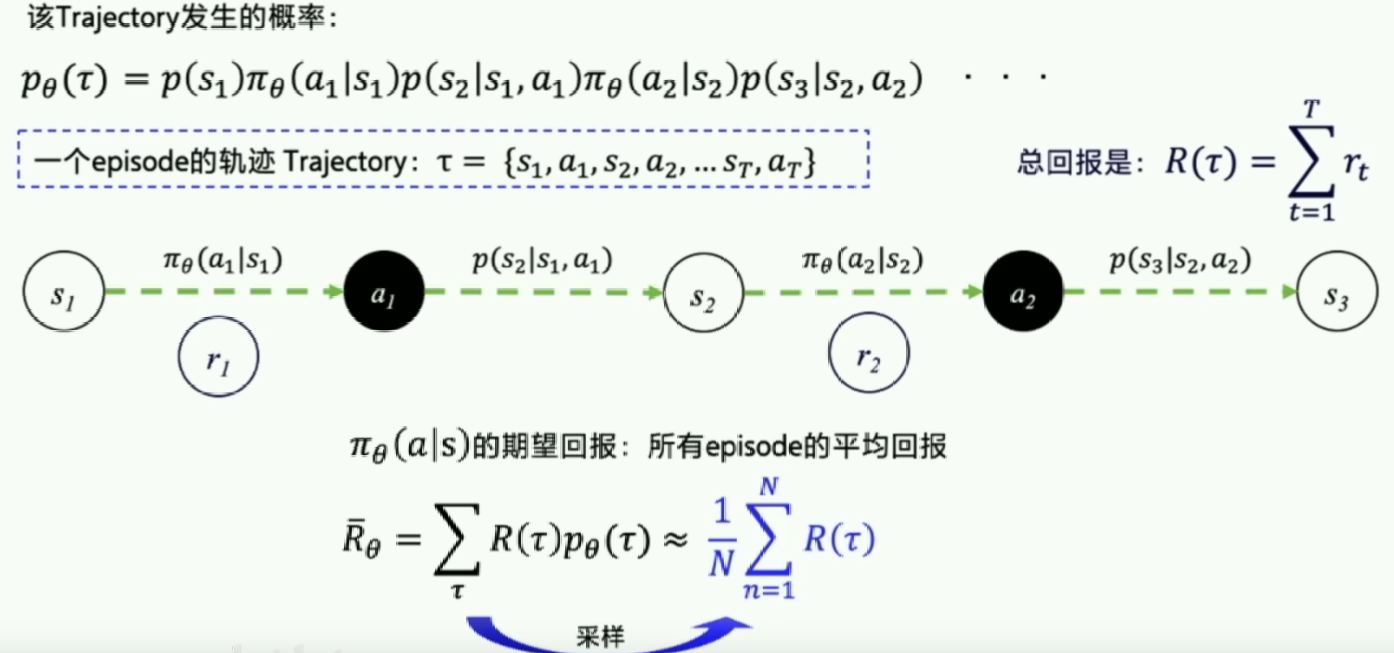当N足够大时可以近似期望回报（采样）。


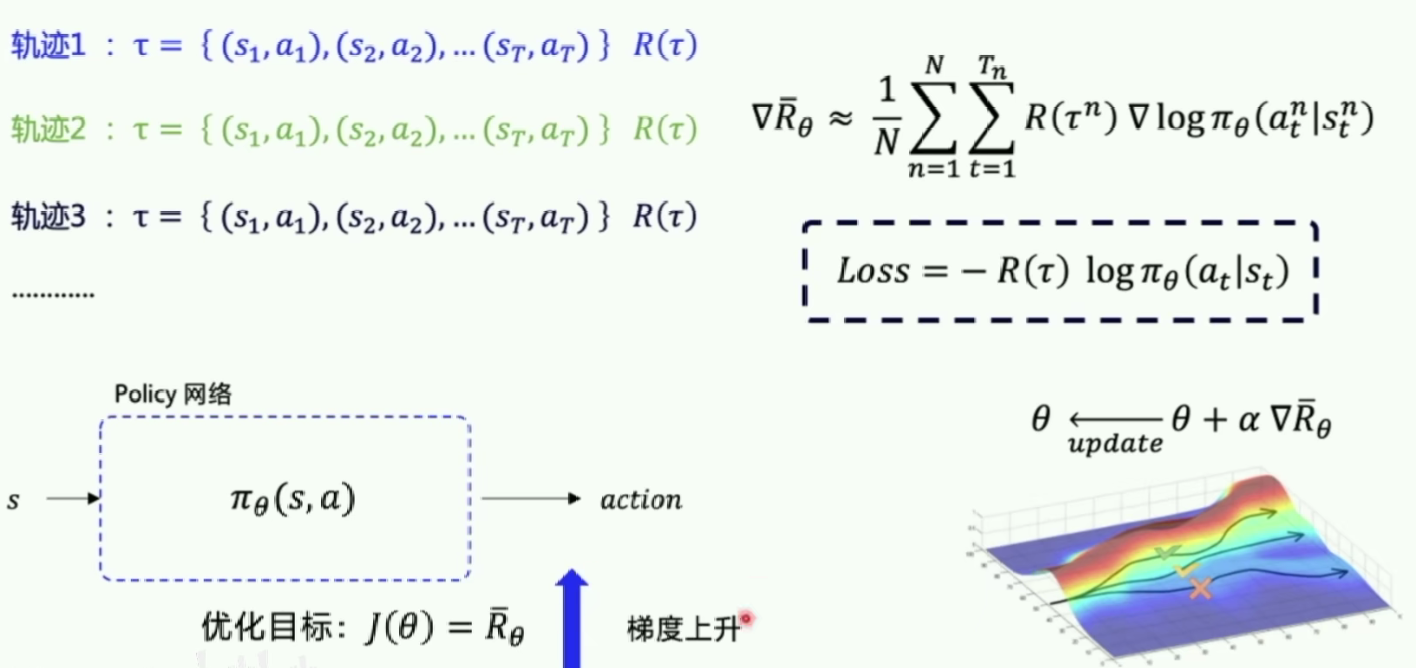
求解 ∇ R θ ˉ \nabla{\bar{R_\theta}} ∇Rθ​ˉ​的具体细节（可以跳过）：

  • 蒙特卡洛与时序差分
    （这里的MC蒙特卡洛方法实际上就是下面的REINFORCE方法，时序差分TD算法是后面要将到的Actor-Critic算法）

Gt是后面的reward之和。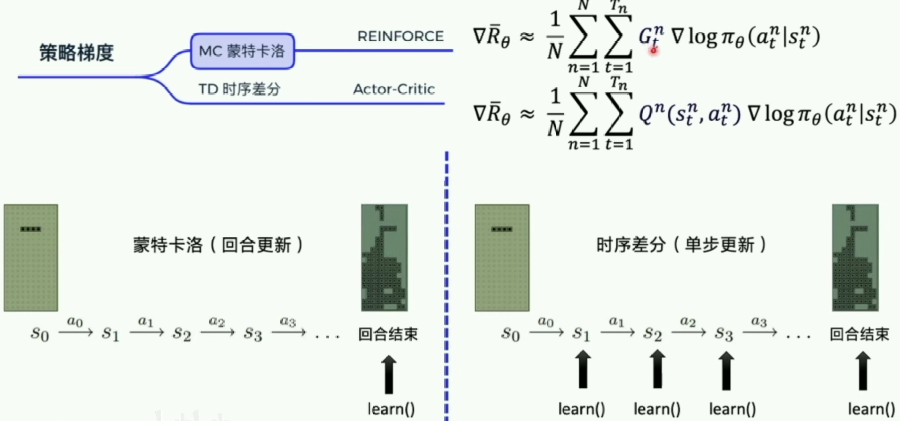

REINFORCE算法因为是一个episode更新，所以在特定的step可以计算后面的reward之和即 G t G_t Gt​。而AC方法是用Q近似 G t G_t Gt​，所以可以做到单步更新。
计算Gt：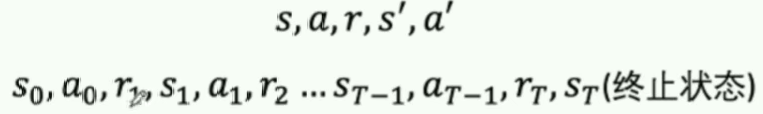

REINFORCE算法：基于 整条回合数据 的更新

Policy gradient的第一个算法是一种基于 整条回合数据 的更新, 也叫 REINFORCE 方法。因为也是NN所以需要梯度下降。


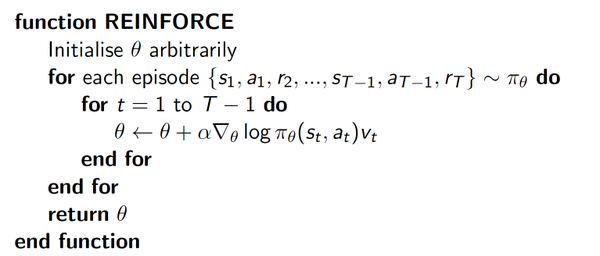
重点：梯度下降里面，希望动作在下一次有机会更多出现， v t v_t vt​告诉我们这个更新方向是否正确，如果正确就更新幅度更大，否则更小。log形式的概率会有更好的收敛性。
∇ θ ( log ⁡ ( p o l i c y ( s t , a t ) ) ∗ V ) \nabla_{\theta}(\log(policy(s_t,a_t))*V) ∇θ​(log(policy(st​,at​))∗V)表示状态S对选择的动作a的吃惊度
代码：github
因为是基于回合的，所以会在回合中的每一次reward进行处理，让reward能更有导向性的引导policy gradient的方向。

for i_episode in range(3000):

    observation = env.reset()

    while True:
        if RENDER: env.render()

        action = RL.choose_action(observation)

        observation_, reward, done, info = env.step(action)

        RL.store_transition(observation, action, reward)    # 存储这一回合的 transition

        if done:
            ep_rs_sum = sum(RL.ep_rs)

            if 'running_reward' not in globals():
                running_reward = ep_rs_sum
            else:
                running_reward = running_reward * 0.99 + ep_rs_sum * 0.01
            if running_reward > DISPLAY_REWARD_THRESHOLD: RENDER = True     # 判断是否显示模拟
            print("episode:", i_episode, "  reward:", int(running_reward))

            vt = RL.learn() # 学习, 输出 vt, 我们下节课讲这个 vt 的作用

            if i_episode == 0:
                plt.plot(vt)    # plot 这个回合的 vt
                plt.xlabel('episode steps')
                plt.ylabel('normalized state-action value')
                plt.show()
            break

        observation = observation_

class PolicyGradient:
    # 初始化 (有改变)
    def __init__(self, n_actions, n_features, learning_rate=0.01, reward_decay=0.95, output_graph=False):

    # 建立 policy gradient 神经网络 (有改变)
    def _build_net(self):

    # 选行为 (有改变)
    def choose_action(self, observation):

    # 存储回合 transition (有改变)
    def store_transition(self, s, a, r):

    # 学习更新参数 (有改变)
    def learn(self, s, a, r, s_):

    # 衰减回合的 reward (新内容)
    def _discount_and_norm_rewards(self):

class PolicyGradient:
    def __init__(self, n_actions, n_features, learning_rate=0.01, reward_decay=0.95, output_graph=False):
        self.n_actions = n_actions
        self.n_features = n_features
        self.lr = learning_rate     # 学习率
        self.gamma = reward_decay   # reward 递减率

        self.ep_obs, self.ep_as, self.ep_rs = [], [], []    # 这是我们存储 回合信息的 list

        self._build_net()   # 建立 policy 神经网络

        self.sess = tf.Session()

        if output_graph:    # 是否输出 tensorboard 文件
            # $ tensorboard --logdir=logs
            # http://0.0.0.0:6006/
            # tf.train.SummaryWriter soon be deprecated, use following
            tf.summary.FileWriter("logs/", self.sess.graph)

        self.sess.run(tf.global_variables_initializer())

 def _build_net(self):
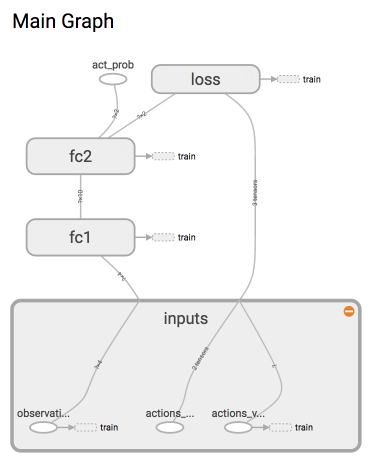
        with tf.name_scope('inputs'):
            self.tf_obs = tf.placeholder(tf.float32, [None, self.n_features], name="observations")  # 接收 observation
            self.tf_acts = tf.placeholder(tf.int32, [None, ], name="actions_num")   # 接收我们在这个回合中选过的 actions
            self.tf_vt = tf.placeholder(tf.float32, [None, ], name="actions_value") # 接收每个 state-action 所对应的 value (通过 reward 计算)

        # fc1
        layer = tf.layers.dense(
            inputs=self.tf_obs,
            units=10,   # 输出个数
            activation=tf.nn.tanh,  # 激励函数
            kernel_initializer=tf.random_normal_initializer(mean=0, stddev=0.3),
            bias_initializer=tf.constant_initializer(0.1),
            name='fc1'
        )
        # fc2
        all_act = tf.layers.dense(
            inputs=layer,
            units=self.n_actions,   # 输出个数
            activation=None,    # 之后再加 Softmax
            kernel_initializer=tf.random_normal_initializer(mean=0, stddev=0.3),
            bias_initializer=tf.constant_initializer(0.1),
            name='fc2'
        )

        self.all_act_prob = tf.nn.softmax(all_act, name='act_prob')  # 激励函数 softmax 出概率

        with tf.name_scope('loss'):
            # 最大化 总体 reward (log_p * R) 就是在最小化 -(log_p * R), 而 tf 的功能里只有最小化 loss
            neg_log_prob = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=all_act, labels=self.tf_acts) # 所选 action 的概率 -log 值
            # 下面的方式是一样的:
            # neg_log_prob = tf.reduce_sum(-tf.log(self.all_act_prob)*tf.one_hot(self.tf_acts, self.n_actions), axis=1)
            loss = tf.reduce_mean(neg_log_prob * self.tf_vt)  # (vt = 本reward + 衰减的未来reward) 引导参数的梯度下降

        with tf.name_scope('train'):
            self.train_op = tf.train.AdamOptimizer(self.lr).minimize(loss)

上面提到了两种形式来计算 neg_log_prob, 这两种形式是一模一样的, 只是第二个是第一个的展开形式. 如果你仔细看第一个形式, 这不就是在神经网络分类问题中的 cross-entropy 吗。
交叉熵计算两个概率分布之间的距离。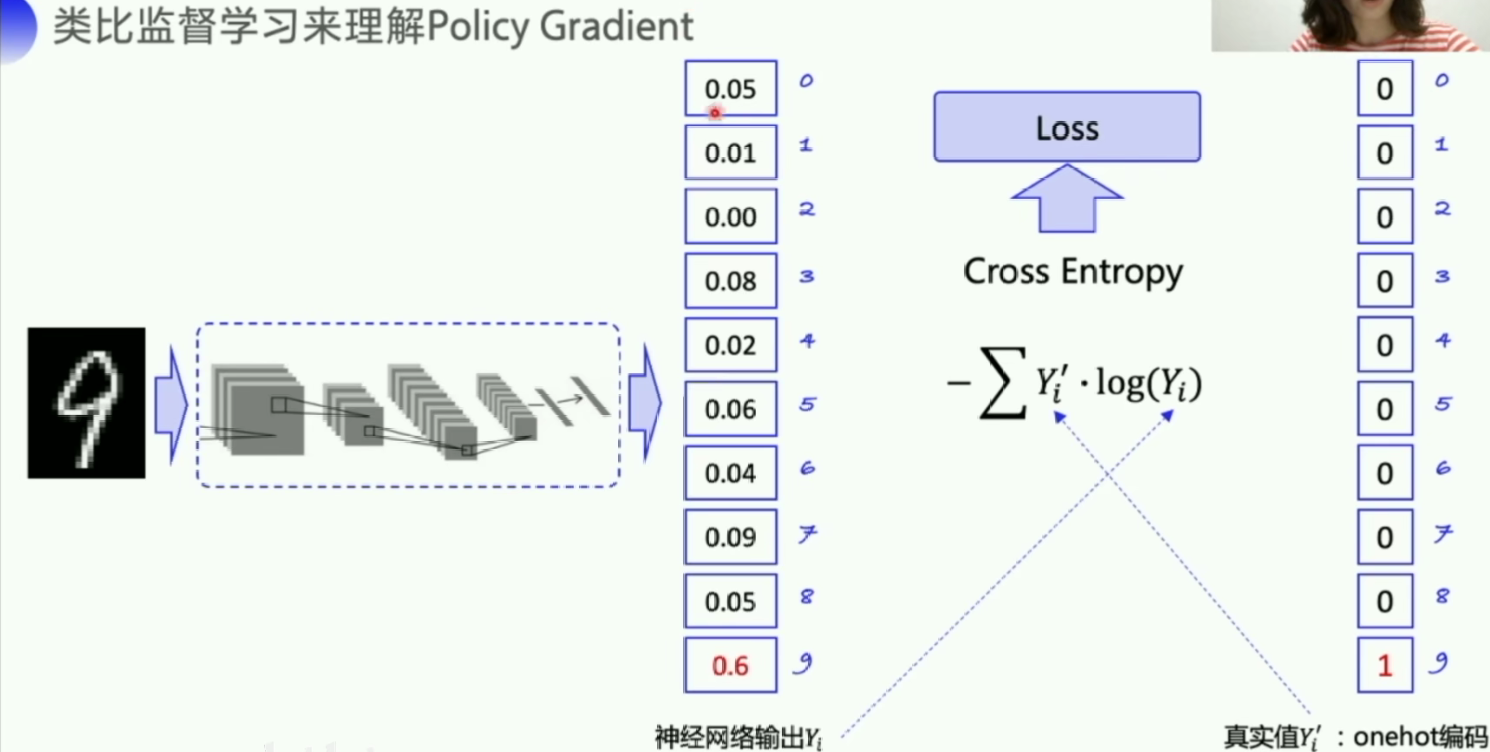


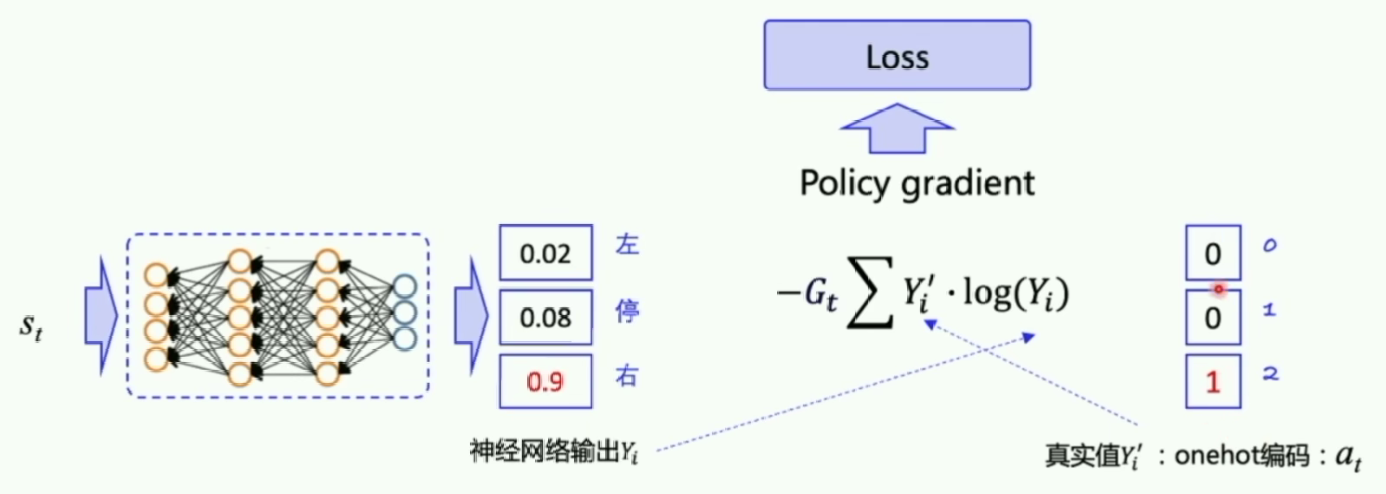
在policy gradient中，真实的action不一定是正确的action，所以还要用上面讲过的reward反馈，因此在外部乘了一个Gt。

（注：R=Gt）

我们的 loss 在原本的 cross-entropy 形式上乘以 vt, 用 vt 来告诉这个 cross-entropy 算出来的梯度是不是一个值得信任的梯度。如果 vt 小, 或者是负的, 就说明这个梯度下降是一个错误的方向, 我们应该向着另一个方向更新参数, 如果这个 vt 是正的, 或很大, vt 就会称赞 cross-entropy 出来的梯度, 并朝着这个方向梯度下降。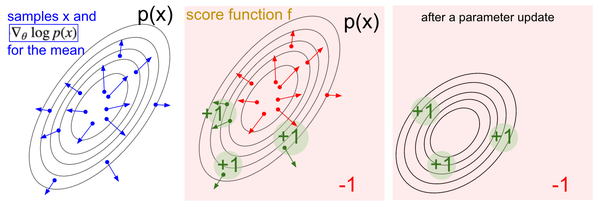

Q:为什么是 loss=-log(prob)vt 而不是 loss=-probvt ?
A:这里的 prob 是从 softmax 出来的, 而计算神经网络里的所有参数梯度, 使用到的就是 cross-entropy, 然后将这个梯度乘以 vt 来控制梯度下降的方向和力度.。

class PolicyGradient:
    def __init__(self, n_actions, n_features, learning_rate=0.01, reward_decay=0.95, output_graph=False):
        ...
    def _build_net(self):
        ...
    def choose_action(self, observation):
        prob_weights = self.sess.run(self.all_act_prob, feed_dict={self.tf_obs: observation[np.newaxis, :]})    # 所有 action 的概率
        action = np.random.choice(range(prob_weights.shape[1]), p=prob_weights.ravel())  # 根据概率来选 action
        return action


def store_transition(self, s, a, r):
        self.ep_obs.append(s)
        self.ep_as.append(a)
        self.ep_rs.append(r)

def learn(self):
        # 衰减, 并标准化这回合的 reward
        discounted_ep_rs_norm = self._discount_and_norm_rewards()   # 功能再面

        # train on episode
        self.sess.run(self.train_op, feed_dict={
             self.tf_obs: np.vstack(self.ep_obs),  # shape=[None, n_obs]
             self.tf_acts: np.array(self.ep_as),  # shape=[None, ]
             self.tf_vt: discounted_ep_rs_norm,  # shape=[None, ]
        })

        self.ep_obs, self.ep_as, self.ep_rs = [], [], []    # 清空回合 data
        return discounted_ep_rs_norm    # 返回这一回合的 state-action value

def _discount_and_norm_rewards(self):
        # discount episode rewards
        discounted_ep_rs = np.zeros_like(self.ep_rs)
        running_add = 0
        for t in reversed(range(0, len(self.ep_rs))):
            running_add = running_add * self.gamma + self.ep_rs[t]
            discounted_ep_rs[t] = running_add

        # normalize episode rewards
        discounted_ep_rs -= np.mean(discounted_ep_rs)
        discounted_ep_rs /= np.std(discounted_ep_rs)
        return discounted_ep_rs

Reference

  1. https://mofanpy.com/tutorials/machine-learning/reinforcement-learning/intro-PG/
  2. 《Policy Gradient Methods for Reinforcement Learning with Function Approximation》NIPS-1999
  3. paddlepaddle-强化学习
  4. 强化学习 10 —— Policy Gradient详细推导
  5. 强化学习 11 —— REINFORCE 算法推导与 tensorflow2.0 代码实现
Logo
魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

cover

【计算机视觉】Pixel逐像素分类&Mask掩码分类理解摘要

avatar 魔乐社区

计算机视觉（opencv）实战三十二——CascadeClassifier 人脸微笑检测（摄像头）

本文从原理到实现，详细介绍了基于 OpenCV Haar 分类器的人脸与微笑检测：讲解了 Haar 特征和级联检测原理。对代码逐行拆解并解释参数含义。画出完整流程图，帮助理解执行过程。给出了常见问题和优化建议，甚至扩展到深度学习方法。这种方法简单、轻量、实时性好，非常适合入门和小型应用项目。但如果需要更高准确率和更强鲁棒性，建议使用深度学习检测器替代 Haar 分类器。

avatar 魔乐社区
cover

小杰机器学习（seven）——贝叶斯分类

avatar 魔乐社区