参考： 《用Python动手学强化》

一、贝尔曼方程

1.1 价值计算

在t时刻选择行动的价值$G_t={\sum }_{k=0}^{T-t-1}{\gamma }^k{r}_{t+1+k}$, 即未来每个时刻的及时奖励乘以折扣率($\gamma$)的累积和。
【注：】

• $\gamma$:折扣率
• $r$: 及时奖励
• t+1+k: 下标表示未来某一时刻
• k: k >= 0 ; k <= T-t-1;
• T：为最终获得奖励的时间

我们可以将这个方程改成递归的形式：
$$G_t=r_{t+1}+\gamma G_{t+1}$$
即我们可以从未来往回逐步估算出$G_t$的值。

1.2 增加策略的价值计算

我们已经知道了一个时刻状态下的期望价值计算方法。那么在加上该状态下的不同行动的行动概率$\pi (a|s)$，以及采取行动后对应的环境中的状态变化的概率$T(s^{\prime }|s,a)$

【注：】

• $\pi (a|s)$: 状态s下采取行动a的概率
• $T(s^{\prime }|s,a)$: 状态s下采取行动a后下一时刻的状态
• s’: 为下一时刻的状态
  
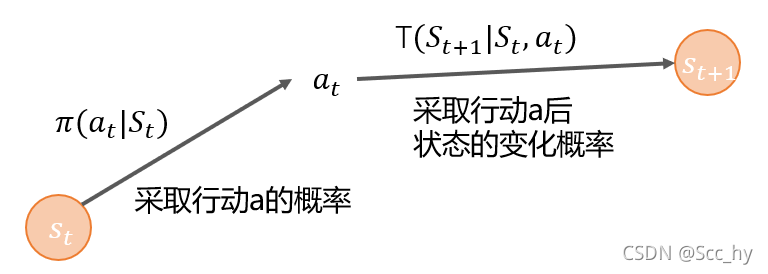
  这样我们就可以得到当前状态的价值了(以相乘的方式计算期望):
  $$V_{\pi }(s)=\sum _a\pi (a|s)\sum _{s^{\prime }}T(s^{\prime }|s,a)[r_{t+1}+\gamma G_{t+1}]$$
  将G统一改为V，t+1用'简化，然后当前的奖励用奖励函数$R$替换，得到最终公式(Bellman Equation)：
  $$V_{\pi }(s)=\sum _a\pi (a|s)\sum _{s^{\prime }}T(s^{\prime }|s,a)[R(s,s^{\prime })+\gamma V(s^{\prime })]$$

当基于价值最大化选择行动的情况下，我们可以对方程修改为下式：
$$V(s)=ma{x}_a\sum _{s^{\prime }}T(s^{\prime }|s,a)[R(s,s^{\prime })+\gamma V(s^{\prime })]$$
如果奖励函数只与当前状态相关，那么可以进一步简化。(下面的脚本主要也是基于这个公式来写的)
$$V(s)=R(s)+\gamma ma{x}_a\sum _{s^{\prime }}T(s^{\prime }|s,a)V(s^{\prime }).........公式(1)$$

二、基于价值的贝尔曼方程实现

主要方程

$$V(s)=R(s)+\gamma ma{x}_a\sum _{s^{\prime }}T(s^{\prime }|s,a)V(s^{\prime }).........公式(1)$$
计算不同状态链路的递归的时候会对一些状态进行重复计算，所以我们用lru_cache做简单优化。

from functools import lru_cache

@lru_cache(maxsize=128)
def V(s, gamma=0.99): # 递归
	# 等价于 公式(1)
    return R(s) + gamma * max_V_on_next_state(s)

奖励函数

def R(s):
    if s == 'happy_end':
        return 1
    elif s == 'bad_end':
        return -1
    else:
        return 0

行动概率与状态转移函数

为了简单示意，我们仅仅定义

• 两个行动
  • UP, DOWN
• 状态转移概率
  • 和行动一致的转移概率90%，和相反行动的转移概率为10%

最终结束条件

• 最多行动5次
  • 当行动少于5次 则返回 {下一状态(s, UP)：概率, 下一状态(s, DOWN)：概率}
• up >= 4次为happy_end, 否则为bad_end

def max_V_on_next_state(s):
    # 如果游戏结束，则期望为0
    if s in ['happy_end', 'bad_end']:
        return 0
    
    actions = ['up', 'down']
    values = []
    for a in actions:
        trainsition_probs = transit_func(s, a)
        v = 0
        for next_state, prob in trainsition_probs.items():
            v += prob * V(next_state) # 递归
        values.append(v)
    # 拿取行动中最大效益的值
    return max(values)


def transit_func(s, a):
	"""
	param s: 状态： 定义成 初始_行动_行动...  如： state_up_down_up | state | state_up 等
	param a: 行动： {'up', 'down'}
	"""
    actions = s.split('_')[1:]
    LIMIT_GAME_COUNT = 5
    HAPPY_END_BORDER = 4
    MOVE_PROB = 0.9

    def next_state(state, action):
        return "_".join([state, action])
    # 结束条件
    if len(actions) == LIMIT_GAME_COUNT:
        up_count = sum([1 if a == 'up' else 0 for a in actions])
        state = 'happy_end' if up_count >= HAPPY_END_BORDER else 'bad_end'
        prob = 1.0
        return {state: prob}
    else:
    	# 状态转移函数
        opposite = 'up' if a == 'down' else 'down'
        return {
            next_state(s, a): MOVE_PROB,
            next_state(s, opposite): 1- MOVE_PROB
        }

简单示例

从所有可能的未来逐步计算到当前。

if __name__ == "__main__":
    # 固定上下走动， 状态叠加在后面
    # state_up_up_up_up_up_up -> 1 + 0                            = 1
    # state_up_up_up_up_up    -> 0 + 0.99 * (0.9*1 + 0.1*1)       = 0.99
    # state_up_up_up_up       -> 0 + 0.99 * (0.9*0.99 + 0.1*0.99) = 0.9801
    print(V('state_up_up_up_up'))
    print(V('state_up_down_up_up'))
    print(V('state_down_up_up_up'))


"""
0.9801
0.78408
0.78408
"""