推荐系统之协同过滤和矩阵分解

1. 基于用户的协同过滤首先就是建立共现矩阵，行是M个样本，列是N个物品，第M行N列代表这个M用户是否对这个N物品感兴趣，感兴趣就点赞，赋值1，没有点赞赋值0然后预测的第一步就是找到与某一个用户最相似的前n个用户预测的第二步就是综合这些相似用户对某一个物品的评价，得出我们要预测用户对这个物品的评价所以这里比较重要的就是怎么计算用户的相似度。其实就是把这些用户点赞的地方是不是大致都一样的。有1.余弦

Francis_s

2343人浏览 · 2021-10-28 19:52:11

Francis_s · 2021-10-28 19:52:11 发布

1. 基于用户的协同过滤

首先就是建立共现矩阵，行是M个样本，列是N个物品，第M行N列代表这个M用户是否对这个N物品感兴趣，感兴趣就点赞，赋值1，没有点赞赋值0
然后预测的第一步就是找到与某一个用户最相似的前n个用户
预测的第二步就是综合这些相似用户对某一个物品的评价，得出我们要预测用户对这个物品的评价

所以这里比较重要的就是怎么计算用户的相似度。

其实就是把这些用户点赞的地方是不是大致都一样的。有

1. 余弦相似度

$sim(i,j) = cos(i,j) = \frac{i*j}{\left \| i \right \| * \left \| j \right \|}$

这个就是衡量向量之间的夹角的大小，夹角越小，这个相似度就越大

2. 皮尔逊相关系数

$sim(i,j) = \frac{\sum_{p\in P}(R_{i,p} - \hat{R_i})(R_{j,p} - \hat{R_j})}{\sqrt{\sum_{p\in P}(R_{i,p} - \hat{R_i})^2} * \sqrt{\sum_{p\in P}(R_{j,p} - \hat{R_j})^2}}$

$R_{i,p}$ 就是用户i对物品p的评分（是否点赞）， $\hat{R_{i}}$ 就是用户i对所有物品的平均评分，P就是所有物品的集合。

我们可以把上面的 $\hat{R_{i}}$ 换成 $\hat{R_p}$ ，这个是所有用户对物品p的平均评分，可以减少物品评分偏置对结果的影响

根据以上公式算出TopN用户后，我们就认为这些用户和我们将要预测的用户的习惯都是非常类似的，所以我们可以根据TopN用户的相似度以及他们对要预测物品p的评分进行一个加权平均。

$R_{u,p} = \sum^N_{i=1}\frac{w_{u,n}}{\sum^N_{i=1}w_{u,n}} * R_{n,p}$

$w_{u,n}$ 就是预测用户u和TopN个用户的相似度，前面一个相当于权重，后面就是TopN个用户分别对物品p的评分了。

然后我们对所有物品都做一个评分，并排序，把分最高的推荐出去

以上就是基于用户的协同过滤算法

2. 基于物品的协同过滤算法

首先就也是构建一个共生矩阵，行是M个样本，列是N个物品，第M行N列代表这个M用户是否对这个N物品感兴趣，感兴趣就点赞，赋值1，没有点赞赋值0
然后计算矩阵两列之间向量的相似性，构建一个n*n的相似度矩阵，这应该是一个对称矩阵，然后某一列/某一行代表着当前这个物品和其余所有物品的相似度
然后根据用户历史行为数据中的正反馈物品列表，什么是正反馈物品列表，就是我在过往的使用数据中，我对那些物品点了赞，就是代表正反馈
利用物品相似度矩阵，我们可以根据正反馈物品列表，获得相似的TopK个物品，形成相似度物品集合，譬如我从里面我的正反馈物品列表有30个，然后我去查这30列，把每列中前3个相似度最高的挑出来，这样我就有30*3个物品，也就是Top90物品列表了
我们对这90个物品进行计算，根据要预测用户对这90物品的评分去算

$R_{u,p} = \sum^N_{i=1} w_{p,i}*R_{u,i}$

$w_{p,i}$ 就是要预测物品与这90个物品的相似度，后面就是当前用户对这个90个物品的打分情况

最后对这个90个物品进行一个排序，生成最终最终的推荐列表，把分最高的推荐出去

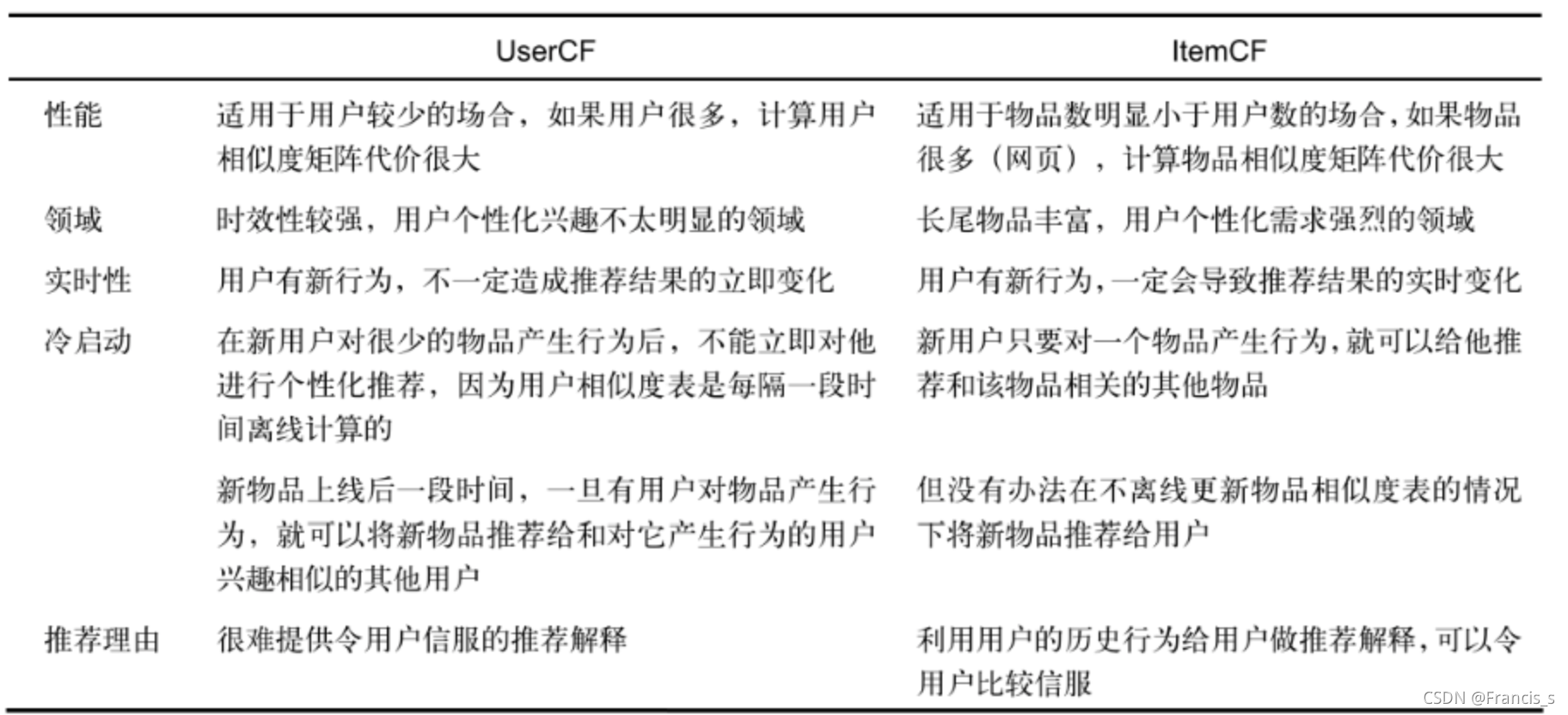
3. 两种算法的对比（书上的内容）

4. 协同过滤的弊端

协同过滤算法无法将两个物品相似的这一信息推广到其他相似的物品上，这就导致了它的泛化能力不是很强。并且会造成热门商品会不断被推荐，冷门就真被打入冷宫的效应。这是为什么呢，我们用基于物品的协同过滤来做解释。

我作为一名用户，看到一件热门商品，肯定是不管我喜不喜欢都点进去都看一下，这里就造成一次点击了，然后我再去点击我感兴趣的，这就会导致热门商品那一列的相似度会非常高，代表着我和我真正喜欢的商品非常相似，也是我感兴趣的，但其实我仅仅是因为它热门我才点的，所以这个热门商品会在基于物品的协同过滤算法中得到正反馈，从而越来越被推荐。

从而造成非热门商品之间的相似性非常非常低，甚至是零，这样协同过滤就没办法找到这些非热门商品之间的联系了，也就是书上的这个图

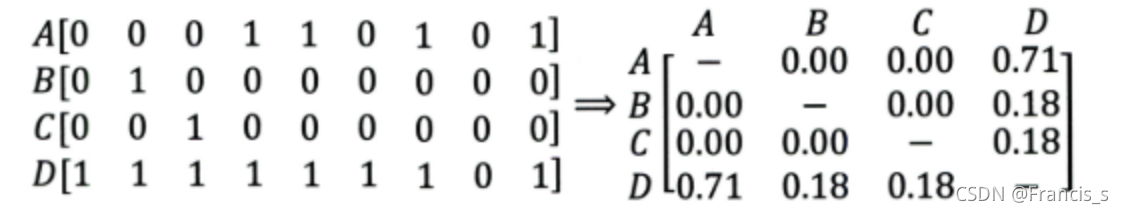
没办法很好地处理稀疏矩阵。所以下面就会引进矩阵分解的去更好地处理稀疏矩阵，我自己理解就是增加模型的复杂度。

5. 矩阵分解

为了解决这种尴尬的局面，我们引入隐向量的概念

这这里不是因为观测不到里面是怎么变换的，而是我们想引进一些变量，就是将模型变复杂，从而提高泛化能力。它的核心思想是通过隐含特征把用户的一些行为（因为点击是跟兴趣有关，所以暂且理解为用户的爱好）和物品联系起来，基于用户的行为（点击），然后对所喜欢的物品进行自动聚类，找出这个用户所喜欢主题和分类。

在矩阵分解的算法框架下，用户和物品的隐向量是通过分解协同过滤生成的共生矩阵得到的，用人话去解释就是

我们不是得到一个共生矩阵嘛，假如是m*n的矩阵，然后我们把这个矩阵分解为

m * k （用户矩阵）和 k * n（物品矩阵）的两个矩阵

k代表隐向量的维度，k的大小决定了隐向量表达能力的强弱，k越大，能包含的信息越多（划分得更加具体），泛化程度越随之降低。

k的取值不是乱来的，它还与矩阵分解的求解复杂度是相关的。k的取值要经过多次试验找到一个推荐效果和工程开销的平衡点。

具体可以用一个例子去解释是怎么划分类别的

通过例子可以发现，我们分解出来的两个矩阵真的非常像一个是基于用户的协同过滤共生矩阵和物品相似性矩阵，真的非常像。隐向量相当于物品了，用户对隐向量（物品）进行评分，构成用户矩阵，然后物品矩阵是物品和隐向量（物品）之间的相似性。

所以我们其实就找到合适的分解矩阵，去更好地抽象出用户兴趣和隐向量的之间的表达，从而提高只有一个共生矩阵时，对稀疏矩阵处理不好的性能。（就是你稀疏嘛，无所谓，我将你分解，你再怎么稀疏，我都可以找到你的兴趣点是啥）

然后就可以进行分数的统计了：

然后现在我们计算用户u对物品i的评分，就是:

$\hat{r_{ui}} = q_i^T*p_u=\sum^N_{i=1}q_{i,k}*p_{k,u}$

第一项就是物品矩阵第i列的向量，第二项就是用户矩阵u在第u行的行向量。

6. 矩阵分解的算法

我们用传统的SVD分解，但是因为共生矩阵大多都是稀疏的，所以我们补全数据，并且维度非常高，所以做分解非常慢。

于是我们改用优化的方式去做这个矩阵分解。

1. 首先就是根据共生矩阵去生成两个空的矩阵，m*k 和 k*n

2. 然后这两个矩阵就是我们引入的隐向量嘛，但是我们现在做分解不好做，于是我们先随机初始化两个分解的value

3. 然后我们的训练数据就是每个用户对每个物品的评分，我们现在将它拆解了（并初始化了），我们现在要算的是根据上面给到的评分公式，利用我们的隐向量去计算用户给物品的评分，然后和训练数据进行一个损失的计算：

$Loss = \sum_{u,i}(Y_{u,i} - \sum^{K}_{k=1}U_{u,k}*I_{k,i})^2$

4. 有了loss之后，这个就变成一个优化问题了。我们可以用梯度下降去做argmin了

下面就是推导梯度下降的公式了：我们其实是想求合适的隐向量的value，所以我们是对评分公式里面的两个参数进行求导：

$\frac{\partial Loss}{\partial U_{u,k}} = -2*(Y_{u,i} - \sum^{K}_{k=1}U_{u,k}*I_{k,i})*I_{k,i}$

$\frac{\partial Loss}{\partial I_{k,i}} = -2*(Y_{u,i} - \sum^{K}_{k=1}U_{u,k}*I_{k,i})*U_{u,k}$

更新梯度：

$U_{u,k} = U_{u,k} -\eta* \frac{\partial Loss}{\partial U_{u,k}}$

$I_{u,k} = I_{u,k} -\eta* \frac{\partial Loss}{\partial I_{k,i}}$

7. 矩阵分解的变种

1. 首先是引入正则项，L1和L2，关于L1和L2的知识点，可以看这里，然后求导就会多了正则化的一项，梯度更新的公式还是不变

2. 考虑了更多更复杂更全面的情况：（这里是参照强哥的博客，算是搬运了，真的写得非常好）

就像我们把很多数值特征一块做特征处理一样，不同的单位会导致不同尺度，所以要统一量纲。

于是我们引入三个偏置项：

$\mu$ : 训练集中所有记录的评分的全局平均数。在不同网站中，因为网站定位和销售物品不同，网站的整体评分分布也会显示差异。比如有的网站中用户就喜欢打高分，有的网站中用户就喜欢打低分。而全局平均数可以表示网站本身对用户评分的影响。

$b_{\mu}$ : 用户偏差系数，可以使用用户u给出的所有评分的均值，也可以当做训练参数。这一项表示了用户的评分习惯中和物品没有关系的那种因素。比如有些用户比较苛刻，对什么东西要求很高，那么他评分就会偏低，而有些用户比较宽容，对什么东西都觉得不错，那么评分就偏高

$b_i$ : 物品偏差系数，可以使用物品i 收到的所有评分的均值，也可以当做训练参数。这一项表示了物品接受的评分中和用户没有关系的因素。比如有些物品本身质量就很高，因此获得的评分相对比较高，有的物品本身质量很差，因此获得的评分相对较低。

于是，整个loss就变成： $Loss = \mu + b_\mu+b_i + U_u*I_i$

然后再引入正则化：

$\small Loss = \sum_{u,i}(r_{u,i} - (\mu + b_\mu+b_i + \sum^K_{k=1}U_{u,k}*I_{k,i}))^2 + \lambda*\mu^2 + \lambda*b_\mu^2 + \lambda b_i^2 + \lambda*U_{u,k}^2 + \lambda*I_{k,i}^2$

继续对那两个参数求导，然后更新梯度就好了

魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

【计算机视觉】Pixel逐像素分类&Mask掩码分类理解摘要

魔乐社区

计算机视觉（opencv）实战三十二——CascadeClassifier 人脸微笑检测（摄像头）

本文从原理到实现，详细介绍了基于 OpenCV Haar 分类器的人脸与微笑检测：讲解了 Haar 特征和级联检测原理。对代码逐行拆解并解释参数含义。画出完整流程图，帮助理解执行过程。给出了常见问题和优化建议，甚至扩展到深度学习方法。这种方法简单、轻量、实时性好，非常适合入门和小型应用项目。但如果需要更高准确率和更强鲁棒性，建议使用深度学习检测器替代 Haar 分类器。