机器学习代价函数求导梯度下降求解最优值源码数据
文章目录前言一、代价函数的产生二、代价函数的定义1.Training set:总结数据前言(文末见数据)在逻辑回归中,我们预测:我们有:hθ(x)=g(θTx),g(z)=sigmoid(z)=11+e−zh_{\theta}(x)=g({\theta}^{T}x),g(z)=sigmoid(z)=\frac{1}{1+e^{-z}}hθ(x)=g(θTx),g(z)=sigmoid(z)=1+
前言
(文末见数据)
在逻辑回归中,我们预测:
我们有: h θ ( x ) = g ( θ T x ) , g ( z ) = s i g m o i d ( z ) = 1 1 + e − z h_{\theta}(x)=g({\theta}^{T}x),g(z)=sigmoid(z)=\frac{1}{1+e^{-z}} hθ(x)=g(θTx),g(z)=sigmoid(z)=1+e−z1
我们得知: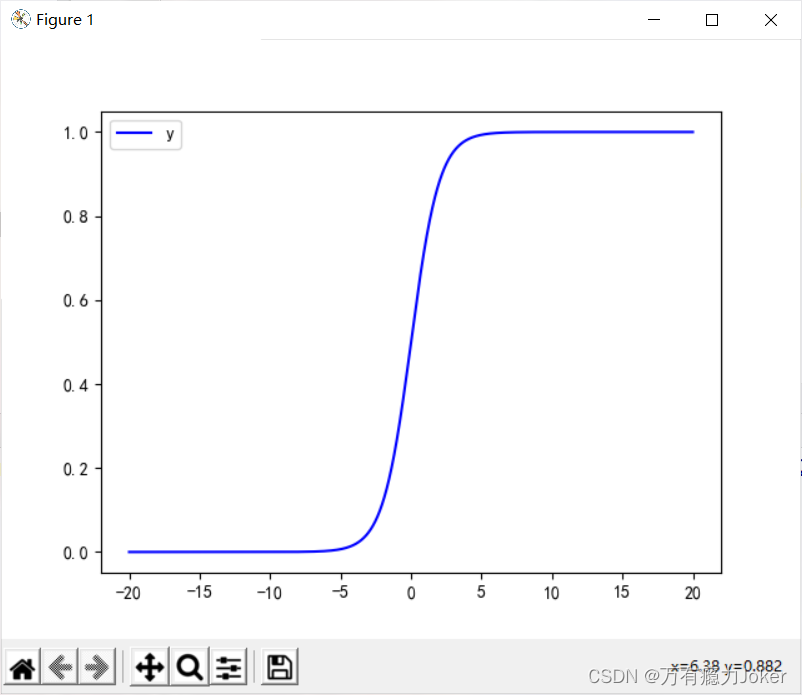
当 h θ ( x ) > = 0.5 h_{\theta }(x)>=0.5 hθ(x)>=0.5时,预测 y = 1 y=1 y=1
当 h θ ( x ) < 0.5 h_{\theta }(x)<0.5 hθ(x)<0.5时,预测 y = 0 y=0 y=0
提示:限于博主的水平,文章难免存在不妥之处,恳请广大读者批评指正!
一、代价函数的产生
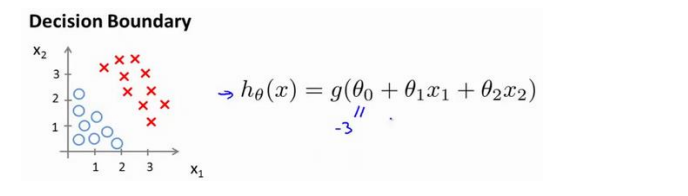
为了让我们更加清楚的了解到自己所创建的模型的好坏,所以我们迫切需要建立一个评估的准则以此来实现更多复杂模型的建立。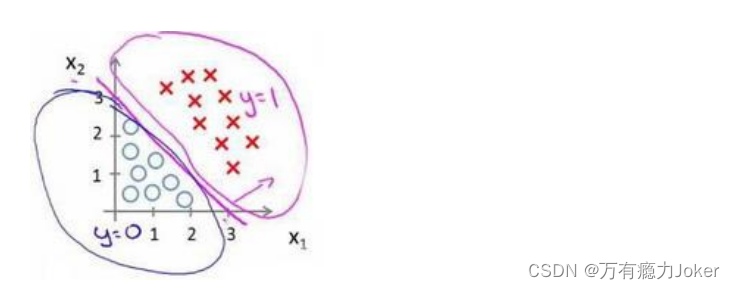
我们通过自己创建的模型来划分数据,怎么的模型才能比较适合呢?所以我们需要定义用来拟合参数的优化目标,或者叫代价函数,这便是监督学习问题中的逻辑回归模型的拟合问题、
二、代价函数的定义
1.Training set:
我们假定给定的训练集如下:
training set:{ ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , . . . . , ( x ( i ) , y ( i ) ) (x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),....,(x^{(i)},y^{(i)}) (x(1),y(1)),(x(2),y(2)),....,(x(i),y(i))}
我们以最简单的只有一维特征的变量 x x x为例:
即 x ( i ) = x i , y ∈ x^{(i)}=x_{i}, y \in x(i)=xi,y∈{0,1}
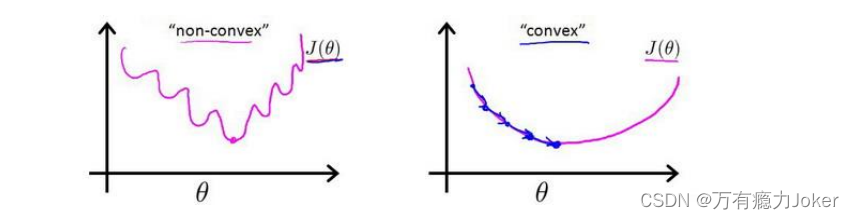
对于线性回归模型,我们定义代价函数是所有模型误差的平方和。我们就得到了:
J ( θ ) = 1 m ∑ i = 1 m 1 2 ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta) = \frac{1}{m}\sum_{i=1}^m\frac{1}{2}(h_{\theta}(x^{(i)})-y^{(i)})^2 J(θ)=m1∑i=1m21(hθ(x(i))−y(i))2
所以求导有:
∂ J ( θ ) ∂ θ = − θ × Σ i = 1 m ( y ( i ) − h θ ( x ) ) \frac{\partial J(\theta)}{\partial \theta}=-\theta\times\Sigma_{i=1}^{m}(y_{(i)}-h_{\theta}(x)) ∂θ∂J(θ)=−θ×Σi=1m(y(i)−hθ(x))
在得到这样一个代价函数以后,我们便可以用梯度下降算法来求得能使代价函数最小的
参数了。
代码:
# 代价函数求导
def partial_derivative_w(x,y,w,b):
result = 0
for i in range(len(x)):
result += (y[i]-f(w,x[i],b))*x[i]*(-1)
return result
def partial_derivative_b(x,y,w,b):
result = 0
for i in range(len(x)):
result += (y[i]-f(w,x[i],b))*(-1)
return result
# M表示最大迭代次数
M = 1000
for i in range(M):
for j in range(len(x)):
c = partial_derivative_w(x,y,w,b)
w = w - a*partial_derivative_w(x,y,w,b)/len(x)
b = b - a*partial_derivative_b(x,y,w,b)/len(x)
w1 = w
b1 = b
if w == w1-a*partial_derivative_w(x,y,w,b)/len(x) and b==b1 - a*partial_derivative_b(x,y,w,b)/len(x):
break
print(w,b,end=' ')
print()
print('w b:',w,b)
总结
例如:以上就是今天要讲的内容,本文仅仅简单介绍了代价函数和使用。
数据
数据第一列表示人口(万),第二列表示某件产品带来利润(万元)
6.1101,17.592
5.5277,9.1302
8.5186,13.662
7.0032,11.854
5.8598,6.8233
8.3829,11.886
7.4764,4.3483
8.5781,12
6.4862,6.5987
5.0546,3.8166
5.7107,3.2522
14.164,15.505
5.734,3.1551
8.4084,7.2258
5.6407,0.71618
5.3794,3.5129
6.3654,5.3048
5.1301,0.56077
6.4296,3.6518
7.0708,5.3893
6.1891,3.1386
20.27,21.767
5.4901,4.263
6.3261,5.1875
5.5649,3.0825
18.945,22.638
12.828,13.501
10.957,7.0467
13.176,14.692
22.203,24.147
5.2524,-1.22
6.5894,5.9966
9.2482,12.134
5.8918,1.8495
8.2111,6.5426
7.9334,4.5623
8.0959,4.1164
5.6063,3.3928
12.836,10.117
6.3534,5.4974
5.4069,0.55657
6.8825,3.9115
11.708,5.3854
5.7737,2.4406
7.8247,6.7318
7.0931,1.0463
5.0702,5.1337
5.8014,1.844
11.7,8.0043
5.5416,1.0179
7.5402,6.7504
5.3077,1.8396
7.4239,4.2885
7.6031,4.9981
6.3328,1.4233
6.3589,-1.4211
6.2742,2.4756
5.6397,4.6042
9.3102,3.9624
9.4536,5.4141
8.8254,5.1694
5.1793,-0.74279
21.279,17.929
14.908,12.054
18.959,17.054
7.2182,4.8852
8.2951,5.7442
10.236,7.7754
5.4994,1.0173
20.341,20.992
10.136,6.6799
7.3345,4.0259
6.0062,1.2784
7.2259,3.3411
5.0269,-2.6807
6.5479,0.29678
7.5386,3.8845
5.0365,5.7014
10.274,6.7526
5.1077,2.0576
5.7292,0.47953
5.1884,0.20421
6.3557,0.67861
9.7687,7.5435
6.5159,5.3436
8.5172,4.2415
9.1802,6.7981
6.002,0.92695
5.5204,0.152
5.0594,2.8214
5.7077,1.8451
7.6366,4.2959
5.8707,7.2029
5.3054,1.9869
8.2934,0.14454
13.394,9.0551
5.4369,0.61705

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献2条内容
已为社区贡献2条内容







所有评论(0)