基于 Delaunay三角剖分的无人驾驶赛车路径规划算法

传统的路径规划算法大多基于栅格地图，存在计算量大、路径精度低等问题。针对这些问题，提供一种基于Delaunay三角剖分的路径规划算法参考，旨在提高路径规划效率和精度。

该算法能够有效地生成安全、平滑、且符合赛道约束的无人驾驶赛车路径，为无人赛车路径规划提供了新的思路和方法。读者可进一步优化路径规划算法，提升路径规划效率和精度，并将其应用于实际的无人驾驶赛车系统中。

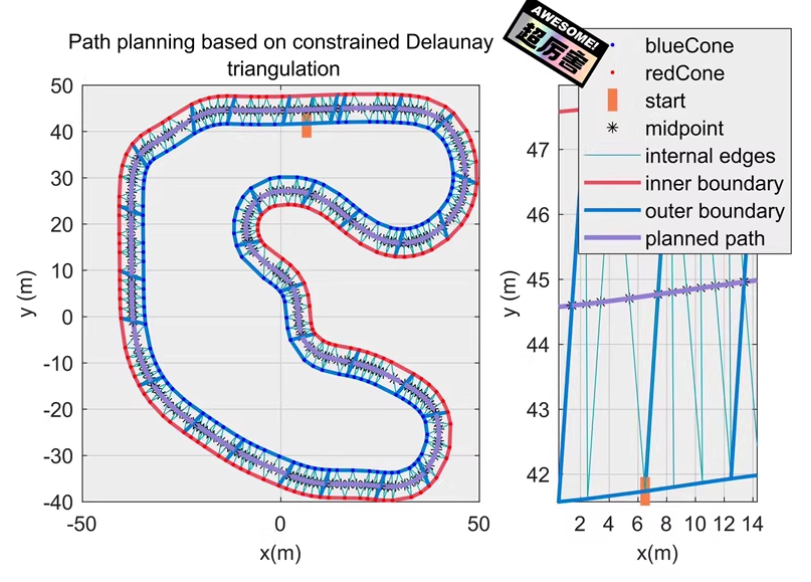
以下文字及示例代码仅供参考

基于 Delaunay三角剖分 的无人驾驶赛车路径规划是一种有效的方法，尤其适用于处理复杂环境下的路径规划问题。这种方法通常涉及将环境表示为一个由障碍物和自由空间组成的二维平面，并使用 Delaunay 三角剖分来创建一个导航网格。然后，可以在这个网格上应用搜索算法（如A*或Dijkstra算法）找到从起点到终点的最优路径。

下面我将提供一个简化的示例，演示如何在 MATLAB 中实现基于 Delaunay 三角剖分的路径规划算法，并附上相应的代码。

示例概述

1. 定义环境：包括起点、终点以及障碍物。
2. 进行 Delaunay 三角剖分：将环境中的点集进行三角剖分。
3. 过滤不可行路径：移除与障碍物相交的边。
4. 应用搜索算法：在生成的导航网格上查找最短路径。
   

MATLAB 实现

步骤 1: 定义环境

% 定义环境参数
startPoint = [0, 0]; % 起点
endPoint = [10, 10]; % 终点
obstacles = [3, 3; 7, 7; 5, 5]; % 障碍物位置（简化示例）

% 创建一些随机点来模拟环境中的自由空间
points = rand(20, 2) * 10;
points = [points; startPoint; endPoint; obstacles];

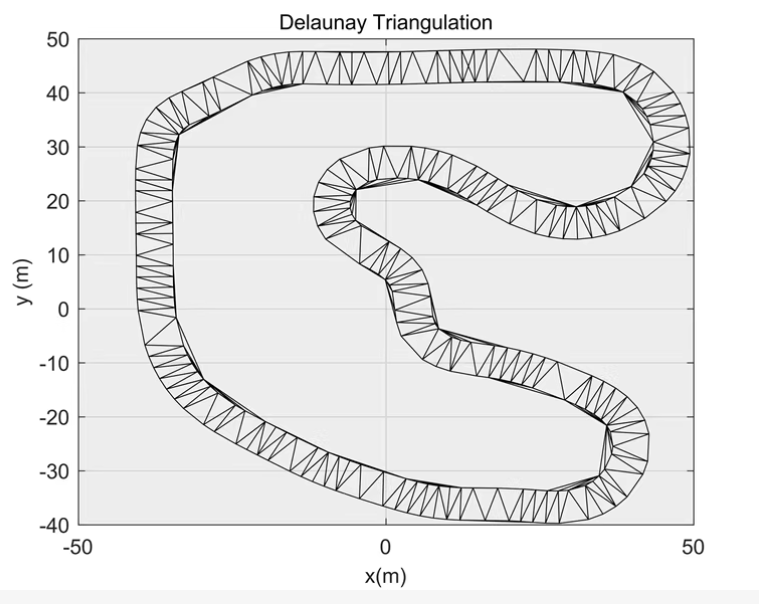
步骤 2: 进行 Delaunay 三角剖分

% 执行 Delaunay 三角剖分
tri = delaunay(points(:,1), points(:,2));

% 可视化三角剖分结果
figure;
triplot(tri, points(:,1), points(:,2));
hold on;
plot(startPoint(1), startPoint(2), 'ro'); % 起点
plot(endPoint(1), endPoint(2), 'go'); % 终点
plot(obstacles(:,1), obstacles(:,2), 'kx', 'MarkerSize', 10); % 障碍物
axis equal;
title('Delaunay Triangulation');

步骤 3: 过滤不可行路径

为了确保路径不穿过障碍物，我们需要检查每条边是否与障碍物相交，并删除那些与障碍物相交的边。

% 初始化邻接矩阵
adjMatrix = zeros(size(points, 1));

% 构建邻接矩阵
for i = 1:size(tri, 1)
    for j = 1:3
        node1 = tri(i, mod(j-1, 3) + 1);
        node2 = tri(i, mod(j+1-1, 3) + 1);
        if ~any(ismember([node1, node2], find(ismember(points, obstacles, 'rows'))))
            adjMatrix(node1, node2) = norm(points(node1,:) - points(node2,:));
            adjMatrix(node2, node1) = adjMatrix(node1, node2);
        end
    end
end

步骤 4: 应用搜索算法

这里我们使用 A* 算法来寻找最短路径。

function path = astar_search(adjMatrix, startIdx, goalIdx)
    % A* 搜索算法实现
    openList = startIdx;
    closedList = [];
    gScore = inf(size(adjMatrix, 1), 1);
    gScore(startIdx) = 0;
    fScore = inf(size(adjMatrix, 1), 1);
    fScore(startIdx) = heuristic(startIdx, goalIdx);

    while ~isempty(openList)
        [~, current] = min(fScore(openList));
        current = openList(current);

        if current == goalIdx
            path = reconstruct_path(cameFrom, current);
            return;
        end

        openList = setdiff(openList, current);
        closedList = [closedList, current];

        neighbors = find(adjMatrix(current,:) > 0);
        for _, neighbor in enumerate(neighbors)
            if ismember(neighbor, closedList)
                continue;
            end

            tentative_gScore = gScore(current) + adjMatrix(current, neighbor);

            if ~ismember(neighbor, openList)
                openList = [openList, neighbor];
            elseif tentative_gScore >= gScore(neighbor)
                continue;
            end

            cameFrom(neighbor) = current;
            gScore(neighbor) = tentative_gScore;
            fScore(neighbor) = gScore(neighbor) + heuristic(neighbor, goalIdx);
        end
    end
    path = [];
end

function h = heuristic(a, b)
    % 使用欧几里得距离作为启发式函数
    h = norm(points(a,:) - points(b,:));
end

function path = reconstruct_path(cameFrom, current)
    totalPath = [current];
    while exist('cameFrom', 'var') && isKey(cameFrom, current)
        current = cameFrom(current);
        totalPath = [current, totalPath];
    end
    path = totalPath;
end

请注意，上述 astar_search 函数是一个简化的实现，您可能需要根据实际情况调整细节。特别是，cameFrom 应该是一个结构体或字典，用于存储每个节点的前驱节点信息。

最后一步：运行并可视化路径

[startIdx, ~] = find(ismember(points, startPoint, 'rows'));
[goalIdx, ~] = find(ismember(points, endPoint, 'rows'));

path = astar_search(adjMatrix, startIdx, goalIdx);

if ~isempty(path)
    plot(points(path, 1), points(path, 2), '-b', 'LineWidth', 2);
    title('Optimal Path with Delaunay Triangulation');
else
    disp('No feasible path found.');
end