1 简介

1. 基本知识

偏最小二乘法是一种新型的多元统计数据分析方法，它通过最小化误差的平方找到一组数据的最佳函数匹配。用最简单的办法去求些未知的真值，使他们的误差平方和最小。这种方法近几十年来，在各领域都得到了迅速发展。偏最小二乘法把固定模式的方法和灵活性的认识巧妙的结合起来了，实现回归建模 ( 多元线性回归 )、数据结构简化 ( 主成分分析 ) 以及两组变量之间的相关性分析( 典型相关分析 )。这是多元统计数据分析中的一个飞跃 。

2 完整代码

%-----最小二乘法方法—
clc;
clear all;  
%% -------数据处理模块------------------
data(1,:)=xlsread('600085.xlsx','E5:E704');
%-----------------数据归一化处理----------
data(2,:)=xlsread('600085.xlsx','B5:B704');
%标准化处理
datamean=mean(data,2);
datastd=std(data,0,2);
Normdata=bsxfun(@minus,data,datamean)./repmat(datastd,1,700);
A1=Normdata(1,:);
B1=Normdata(2,:);
C=data(1,:);
trainP=B1(1:600);   %训练输入数据
trainT=A1(1:600);    %训练输出数据
preInput=B1(601:700);  %预测输入数据
targetOutput=C(601:700);  %目标数据

%% ----- 最小二乘法--------------
A=trainP*trainT'*inv(trainT*trainT');
%预测阶段
preP=A*preInput;


%% 反归一化处理
for i=1:length(preP)   %对预测输出的数据进行反归一化
  preOut(i)=preP(i)*datastd(1,:)+datamean(1,:);
end
%误差处理
errorMes=targetOutput-preOut;
%% 作图比较
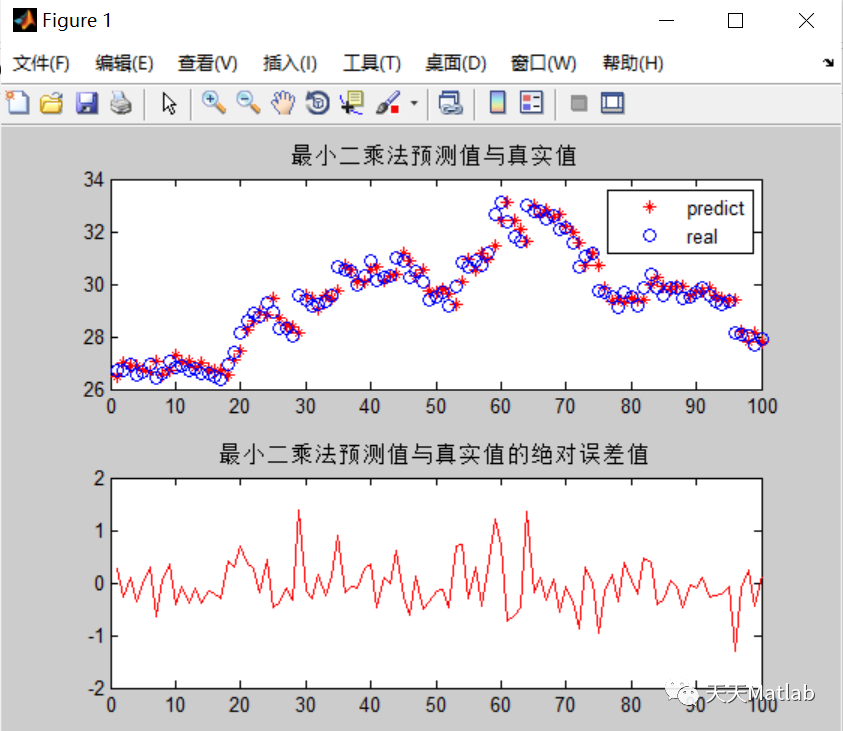
figure(1);
subplot(2,1,1);
plot(1:100,preOut,'r*',1:100,targetOutput,'bo');
legend('predict','real');
title('最小二乘法预测值与真实值');
subplot(2,1,2);
plot(errorMes,'r');
title('最小二乘法预测值与真实值的绝对误差值');

3 仿真结果

4 参考文献

[1]李雪莲, 孙尧, & 莫宏伟. (2009). 基于最小二乘法的冗余信息数据融合算法实现. 计算机工程与应用, 45(15), 5.