Floyd 算法介绍

是解决给定的加权图中顶点间的最短路径的一种算法，可正确处理有向图的最短路径问题
是一个基于贪心、动态规划，求一个图中 所有点到所有点 最短路径的算法

Floyd算法详解 通俗易懂
最短路径问题—Floyd算法详解

Floyd.m

clc
clear
close all

t0=cputime;
%% 栅格界面、场景定义
% 行数和列数
rows = 20;
cols = 30;
[field, cmap] = defColorMap(rows, cols);

% 起点、终点、障碍物区域
startPos = 2;
goalPos = rows * cols - 2;
field(startPos) = 4;
field(goalPos) = 5;

%% 算法初始化
n = rows * cols;        % 栅格节点总个数
map = inf(n, n);        % 所有节点间的距离map
path = cell(n ,n);      % 存放对应的路径
for startNode = 1 : n
    if field(startNode) ~= 2
        neighborNodes = getNeighborNodes(rows, cols, startNode, field);
        for i = 1 : 8
            if ~(isinf(neighborNodes(i, 1)) || isinf(neighborNodes(i, 2)))
                neighborNode = neighborNodes(i, 1);
                map(startNode, neighborNode) = neighborNodes(i, 2);
                path{startNode, neighborNode} = [startNode, neighborNode];
            end
        end
    end
end
for i = 1 : n
    for j = 1 : n
        if  j ~=i
            for k = 1 : n
                if k ~= i && k ~= j
                    if map(j, i) + map(i, k) < map(j, k)
                        map(j, k) = map(j, i) + map(i, k);
                        path{j, k} = [path{j, i}, path{i, k}(2 : end)];
                    end
                end
            end
        end
    end
end

elapsed_time=cputime-t0
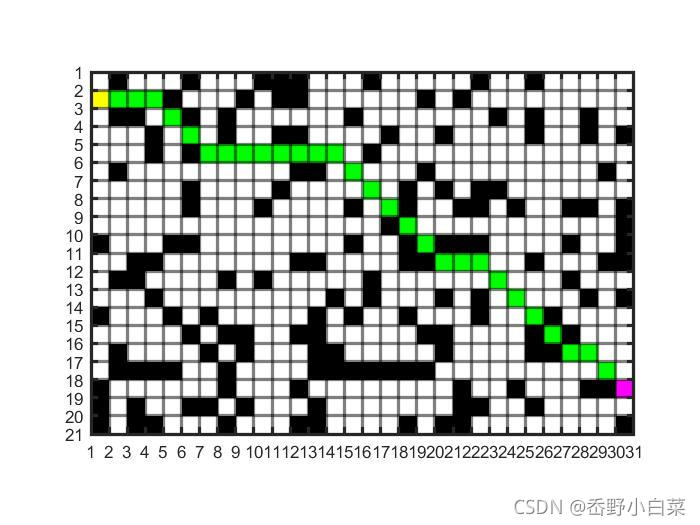
%% 画栅格界面
% 找出目标最优路径
path_opt = path{startPos, goalPos};
field(path_opt(2 : end - 1)) = 6;

% 画栅格图
image(1.5, 1.5, field);
grid on;
set(gca, 'gridline', '-', 'gridcolor', 'k', 'linewidth', 2, 'GridAlpha', 0.5);
set(gca, 'xtick', 1 : cols + 1, 'ytick', 1 : rows + 1);
axis image;