【UWB姿态估计】通过UWB测量进行高效的平面姿态估计——2D仿真(Matlab代码实现)
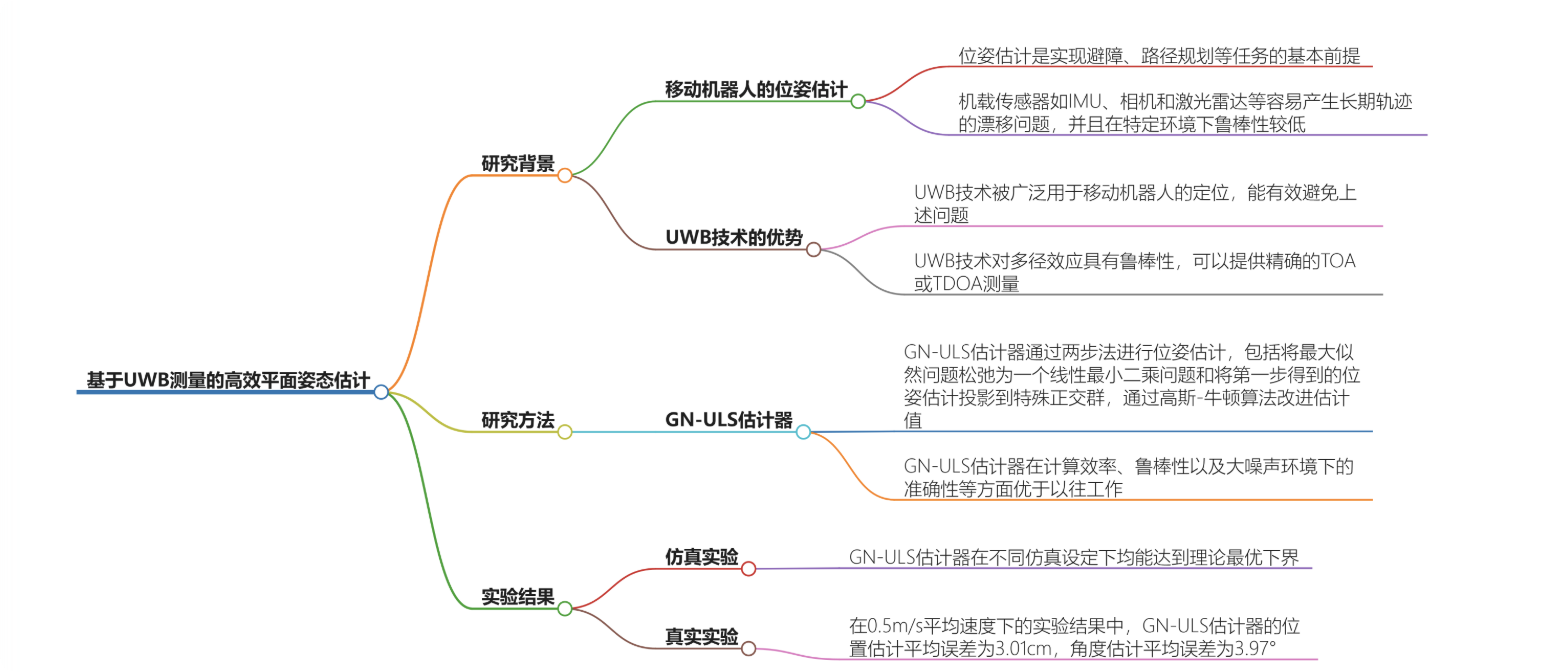
摘要——状态估计在自主驾驶中扮演着至关重要的角色系统。集成超宽带(UWB)技术已被证明可以纠正长期估计偏差并绕过环闭合检测的复杂性。然而,关于机器人技术将UWB视为一种独立的状态估计解决方案。这项工作的主要目的是研究平面姿态仅使用UWB距离测量进行估计。我们证明两步方案的优良特性,也就是说我们可以通过以下方式将一致估计量改进为渐近有效的估计量高斯-牛顿迭代的一个步骤。基于这一结果,我们设计GN-U
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能解答你胸中升起的一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
摘要——状态估计在自主驾驶中扮演着至关重要的角色系统。集成超宽带(UWB)技术
已被证明可以纠正长期估计偏差并绕过环闭合检测的复杂性。然而,关于机器人技术将UWB视为一种独立的状态估计解决方案。这项工作的主要目的是研究平面姿态仅使用UWB距离测量进行估计。我们证明两步方案的优良特性,也就是说我们可以通过以下方式将一致估计量改进为渐近有效的估计量高斯-牛顿迭代的一个步骤。基于这一结果,我们设计GN-ULS估计器,减少计算量
与以前的方法相比,时间明显缩短,并提出了仅使用UWB进行实时状态估计的可能性。
状态估计是智能移动机器人实现诸如避障和路径规划等任务的基本前提。近年来,人们投入了大量精力,利用机载传感器(如惯性测量单元、摄像头和激光雷达)来实现高性能和实时的状态估计。然而,这些方法面临着长期漂移[1]以及在几何退化环境中鲁棒性低[2]等问题。为了克服上述挑战,我们可以在状态估计中整合外部信息,如全球定位系统(GPS)[3]。
超宽带(UWB)是一种对多径效应具有鲁棒性的无线电技术,能够提供精确的到达时间(TOA)或到达时间差(TDOA)测量[4]。UWB传统上用于定位[5]–[9],而许多近期的研究工作[10]–[13]将UWB整合进来,以实现在GPS拒止环境中的无漂移状态估计。然而,很少有机器人研究工作探讨独立使用UWB进行姿态估计。
本研究考虑仅通过采用对称双向TOA测量技术获得的UWB测距测量来估计机器人的姿态。我们关注图1所示的平面情况。
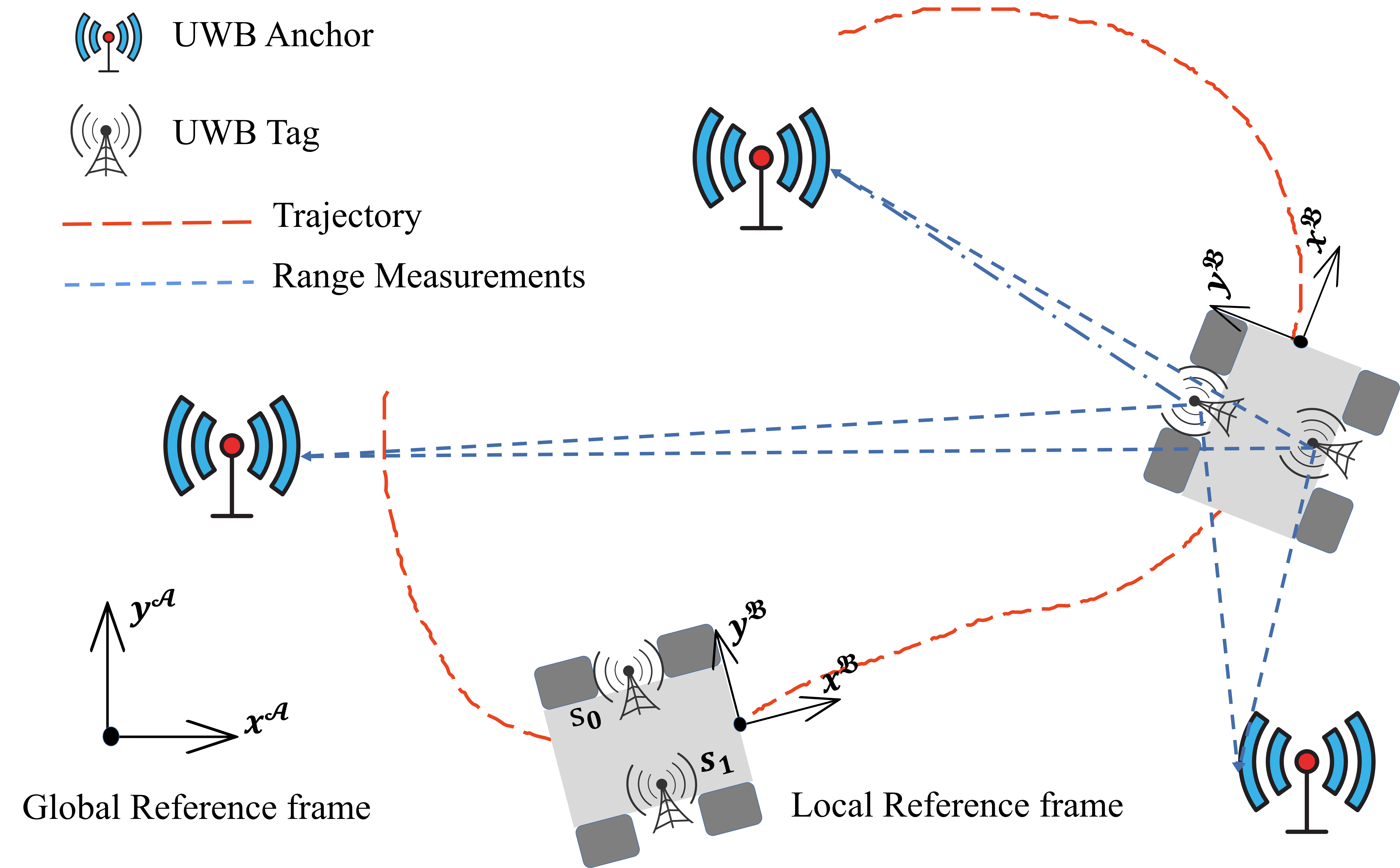
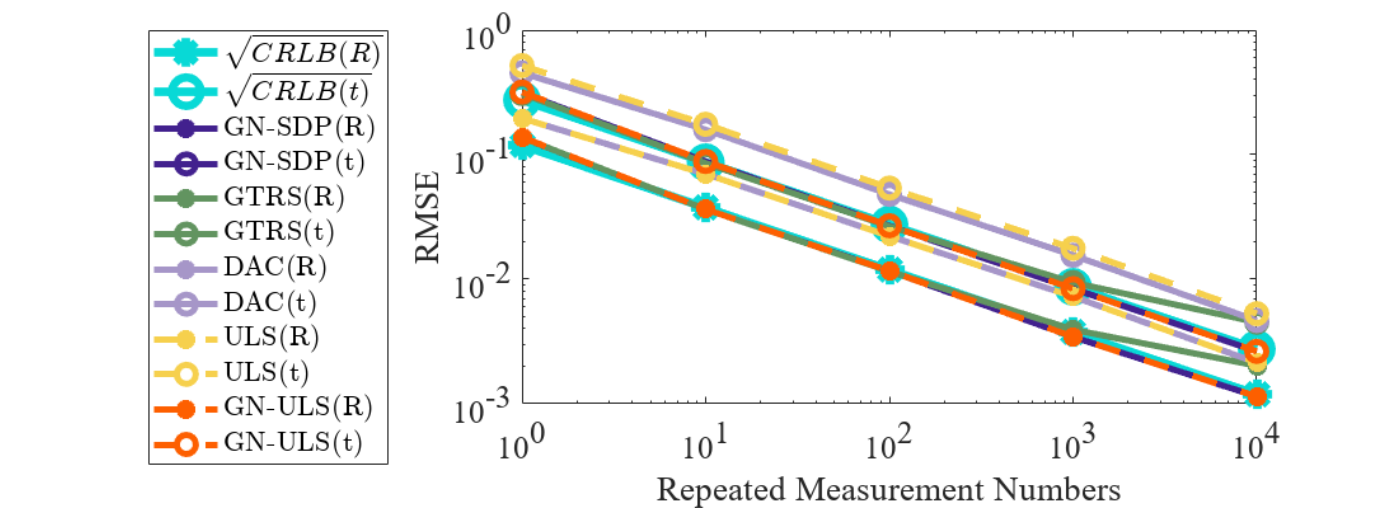
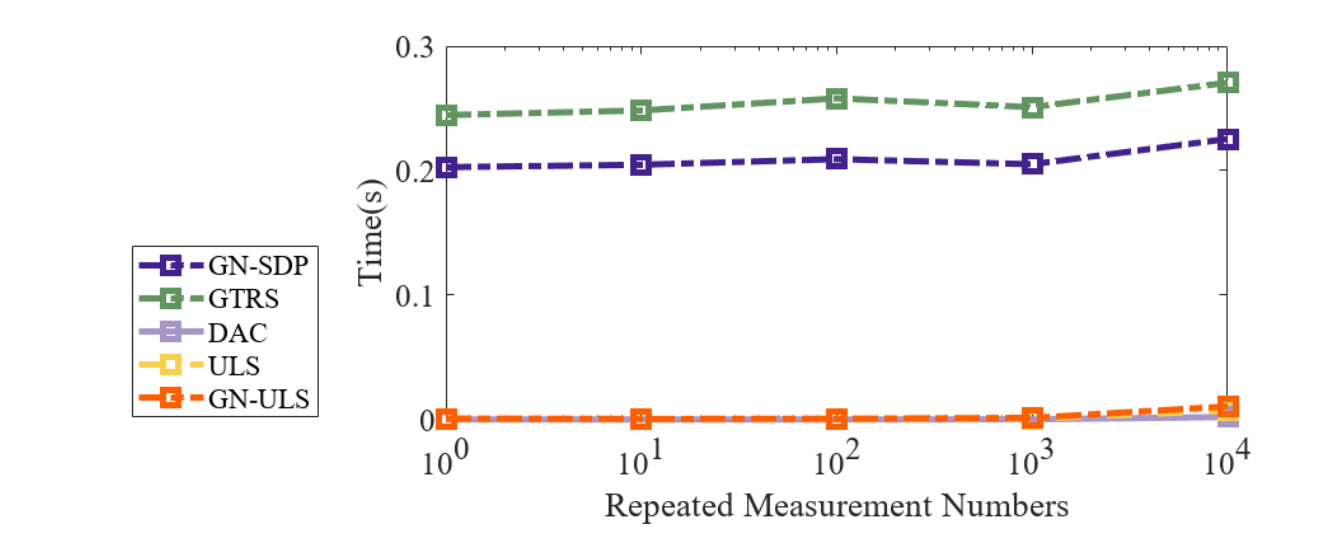
图1:通过UWB测量进行平面姿态估计,例如搜救机器人[14]和室内服务机器人[15]。我们将此问题视为信号处理领域中的刚体定位(RBL)问题。通过文献综述,我们发现姿态估计器的统计效率尚未得到充分研究,且估计器的计算复杂度需要进一步降低,以实现实时估计。在本工作中,我们采用两步方案并开发了一种闭式估计器,该估计器在与锚点几何形状相关的温和条件下渐近有效,并显著减少了计算时间。我们还进行了仿真和实验,以展示我们方法的统计和计算效率。
B. 平面刚体定位的相关工作 在假设独立同分布高斯噪声的情况下,RBL的最大似然(ML)表述是一个受约束的加权最小二乘(LS)问题(2)。然而,由于(2)的非凸性和非线性,ML估计难以获得。常见的做法是对平方测距数据应用最小二乘方法,并构建平方最小二乘(SLS)问题(6)。 据我们所知,文献[16]是首次对RBL问题进行表述,提出通过对平方测量数据进行投影,将其投影到单位向量的零空间来修改SLS问题。这一操作消除了二次项,使问题线性化,文献[17]和我们的工作都沿用了这一思路。我们将得到的表述(7)称为投影平方最小二乘(PSLS)。基于PSLS,文献[16]通过高斯-牛顿算法求解加权正交Procrustes问题,并从具有闭式解的更简单问题中获得初始值。文献[16]还推导出了酉约束克拉美罗下界(CRLB)。文献[17]利用旋转矩阵的结构,构建了一个广义信赖域子问题(GTRS),并通过在线性化的SLS问题上进行一步高斯-牛顿迭代来细化解。文献[18]使用半定松弛,将SLS表述为半定规划(SDP),并通过在ML问题上进行一步高斯-牛顿迭代来细化解。 综上所述,平面RBL问题的ML估计难以获得。以往的研究转向SLS问题,并采用不同技术使问题线性化。然而,早期的研究并未严格评估所提出的估计器与ML估计器的偏差或其统计效率。考虑到对可证明最优状态推断[19]日益增长的兴趣,我们认为这些主题值得仔细研究。理论结果也激励了更快最优估计器的设计。
此部分为2D仿真部分。
📚2 运行结果
2.1 测试1


2.2 测试2
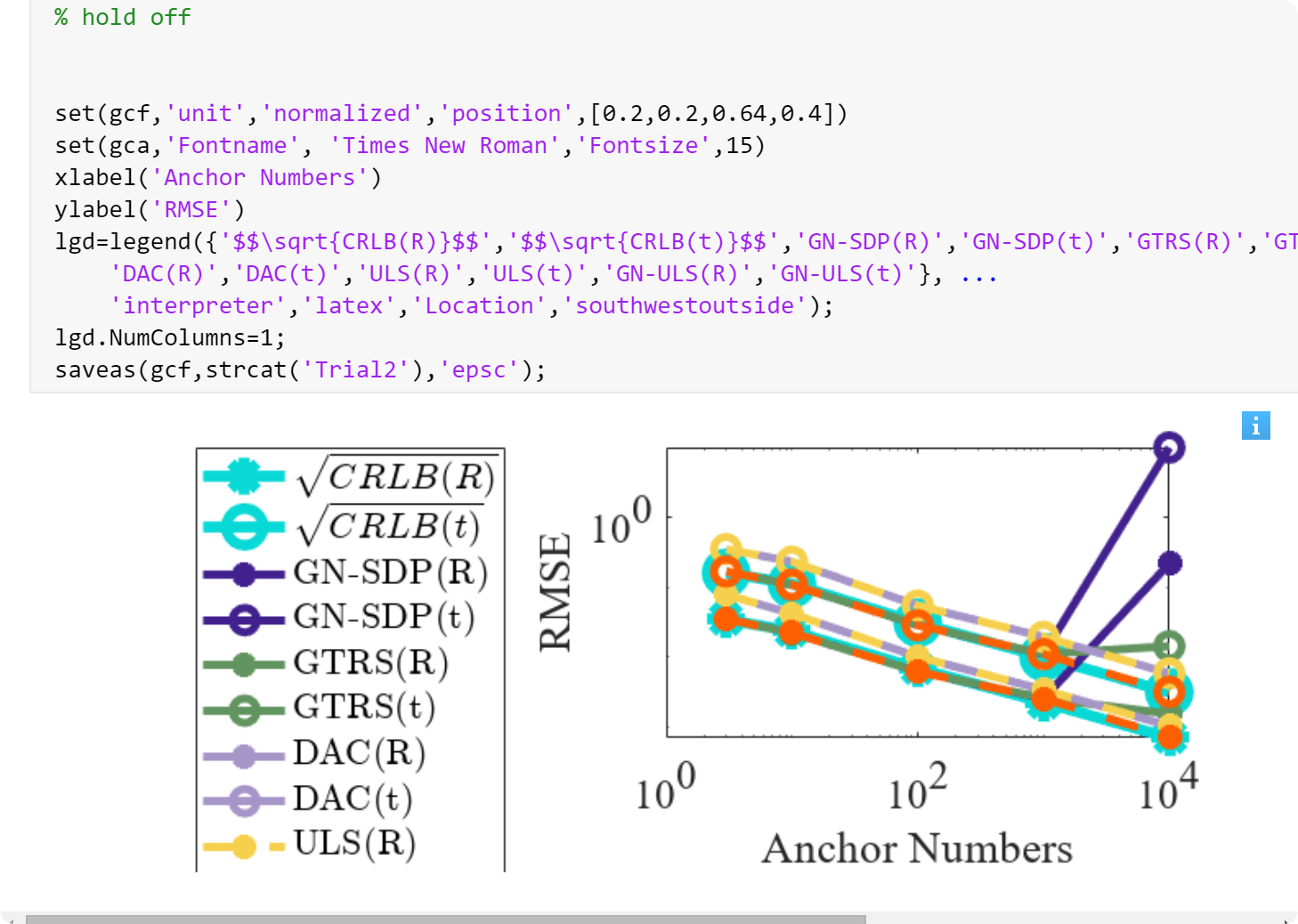
2.3 测试3

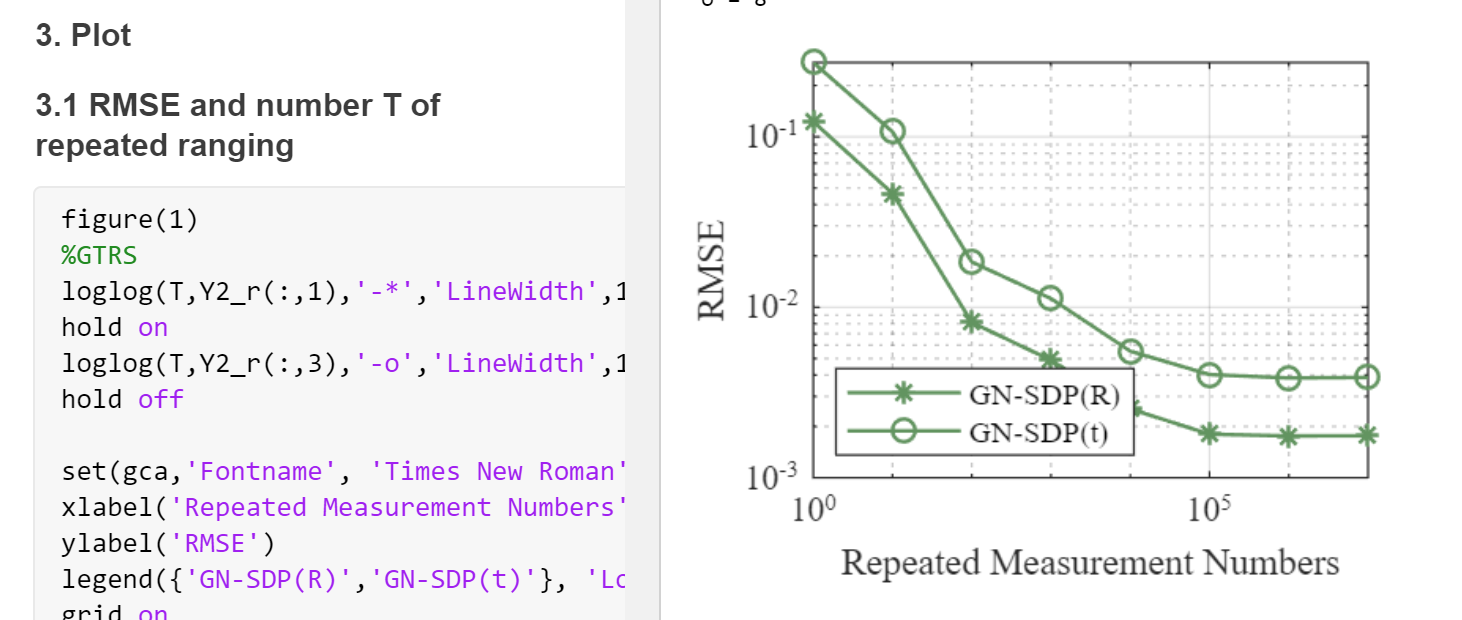
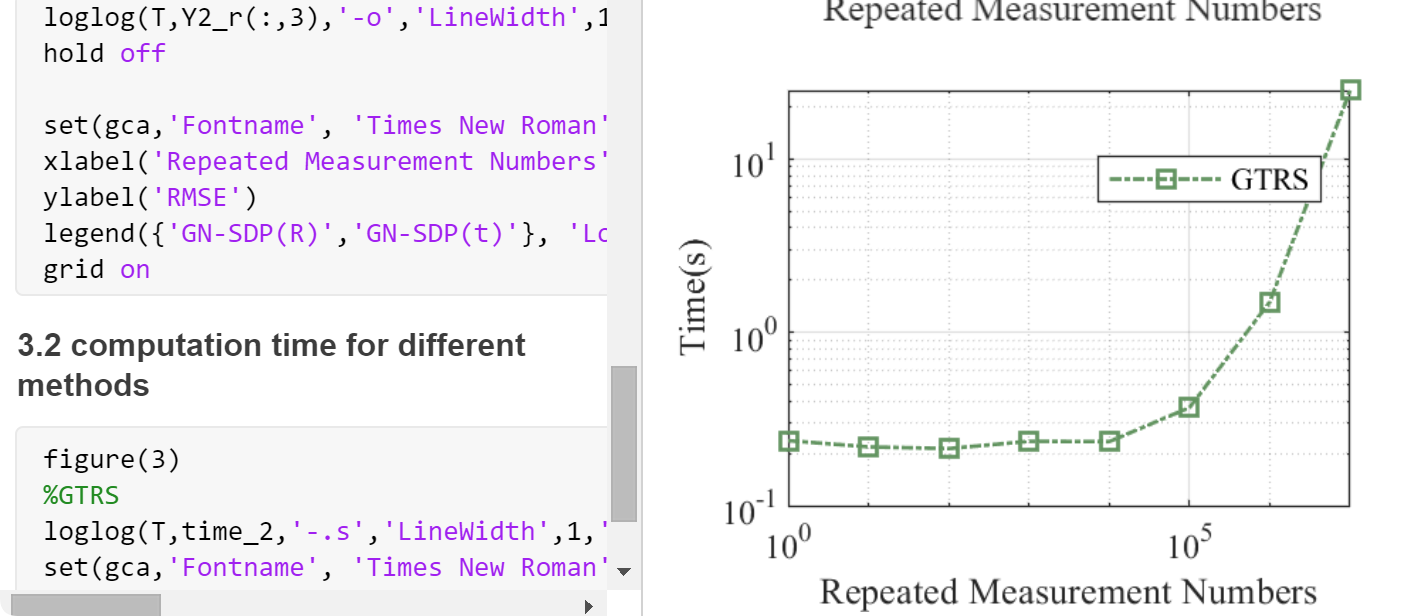
部分代码:
function [y,t,time]=GTRS(E1,E2,Rn,D,Mt,N)
%Input
%E1(Mt*N,2) :
%E2(Mt*N,2) :
%Rn(Mt*N,1) : standard deviations
%D(Mt*N,1) :
%Mt
%N :
%Output
%y(2,1) :
%t(2,1) :
%time : running time of certain part
time=0;
EE=E2'./repmat(Rn',2,1);%2*MN
EEE=(EE*E2)\EE; %
ppE1=(E1-E2*(EEE*E1))./repmat(sqrt(Rn),1,2);
ppD=(D-E2*(EEE*D))./sqrt(Rn);
AtA_mn=(ppE1'*ppE1)/(Mt*N);
Atb_mn=(ppE1'*ppD)/(Mt*N);
% cvx_begin sdp quiet;
% variable lambda_l;
% minimize(lambda_l);
% AtA_mn+lambda_l*C>=0;
% cvx_end;
% time=time+toc;
syms lambda real
theta_lambda=(AtA_mn+lambda*eye(2))\Atb_mn;
phi_lambda=theta_lambda'*theta_lambda-1;
[n,~]=numden(phi_lambda);
sol_lambda=real(double(solve(n==0,lambda,'MaxDegree','4')));
sol_lambda=max(sol_lambda);
% if sol_lambda<=lambda_l
% error('singular case!')
% end
% tic
y2=(AtA_mn+sol_lambda*eye(2))\Atb_mn;
y=y2/norm(y2);
t=EEE*(D-E1*y2);
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。(文章内容仅供参考,具体效果以运行结果为准)

🌈4 Matlab代码、数据、文章下载
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取


魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容







所有评论(0)