Gamma 变换详解：图像增强与显示系统的应用

本文系统介绍了Gamma变换在图像处理中的应用。Gamma变换是一种非线性灰度映射方法，其核心原理是通过幂函数调整图像亮度，匹配人眼对暗部更敏感的特性。文章首先通过夜景照片示例说明Gamma变换的必要性，详细推导了数学公式及导数性质，展示了不同参数下的曲线特征。在应用方面，通过两个典型案例（曝光不足和过度的风景照）演示了Gamma变换如何有效调节亮度和对比度，并给出完整的C++实现代码及优化方案。

luofeiju

2460人浏览 · 2025-07-10 16:27:39

luofeiju · 2025-07-10 16:27:39 发布

初识Gamma变换

在图像处理与显示系统中，Gamma 变换是一种非线性灰度映射方法，它的核心目的是匹配人眼对亮度的感知特性。我们先从一个生活中常见的例子讲起：

你是否注意到，在拍摄夜景或阴影中的物体时，手机拍摄的图像比肉眼所见更暗，细节也更难辨认？这是因为图像传感器线性响应光线，而人眼对亮度是非线性感知的。人类的视觉系统对低亮度比高亮度更敏感，这意味着我们能在黑暗中分辨出非常微小的亮度差异，但在高亮区域的感知能力却较弱。Gamma 变换的存在，正是为了弥合这种设备与人眼感知差异。

在图像增强领域中，通过Gamma可以实现亮度调整与对比度增强。如低光环境中的图像，使用小于1的Gamma值可提升暗部细节。

在图像编码中，Gamma变换不仅是亮度调节工具，它还发挥着压缩冗余信息、提升存储效率的重要作用。如在JPEG编码中，使用Gamma变换后可保留更多图像细节（人眼敏感的暗部区域），因此在量化与压缩时可减少失真。在图像显示过程时，显示设备对输入图像进行还原，最终呈现给用户一个线性响应，使得用户可以看到真实画面。

在后续内容中，我们会分别讨论Gamma在图像增强以及编码显示上的应用。在讨论应用之前，我们首先要从原理上了解Gamma变换的一些数学特性，以便于我们可以比较深刻的理解应用场景。当然，你也可以对数学特性作简单的了解即可，这样似乎不太影响对Gamma变换的理解。

Gamma变换的数学原理

基本定义

对于输入像素值 $x\in [0,1]$ ，Gamma 变换的数学形式为： $y=x^{\gamma}$ ，其中：

$x$ ：归一化后的输入像素值（通常是将 8 位图像除以 255 得到的 0~1 区间数值）；
$\gamma$ ：控制图像亮度和对比度的幂指数参数，取值范围： $\gamma \in (0,+\infty)$ ；
$y$ ：输出像素值，仍在 [0,1] 区间。

导数及其性质

$y^{'}=\gamma x^{(\gamma - 1)}$ ， $y{''}=\gamma (\gamma - 1)x^{(\gamma - 2)}$

以下给出导数的推导：

由于 $ln^{x}\leftrightarrow e^{x}$ 为一对反函数， $y=e^{x} \rightarrow x=ln^{y}\rightarrow y=e^{ln^{y}}$ ，

通过替换变量， $y=e^{ln{y}}$ 可表示为 $x=e^{ln^{x}}$ ，

将上市代入 $y=x^{\gamma}$ 得： $y=(e^{ln^{x}})^{\gamma}=e^{\gamma ln^{x}}$ ，

为什么需要如此改写函数，这里主要利用了自然对数的一些特性，使得求导更加统一且方便。

令 $u(x)=\gamma ln^{x}$ 将上式改写成复合函数： $y=e^{u(x)}$ ，利用链式法则求导：

$y^{'}=e^{u(x)}u^{'}(x)=e^{u(x)}\frac{\gamma}{x}$ ，将中间函数 $u(x)$ 代入得：

$y^{'}=e^{\gamma ln^{x}}\frac{\gamma}{x}=x^{\gamma}\frac{\gamma}{x}=\gamma x^{\gamma - 1}$ ，因此一阶导数得证。使用同样方式可证明二阶导数。

下面给出不同 $\gamma$ 取值下得Gamma曲线：

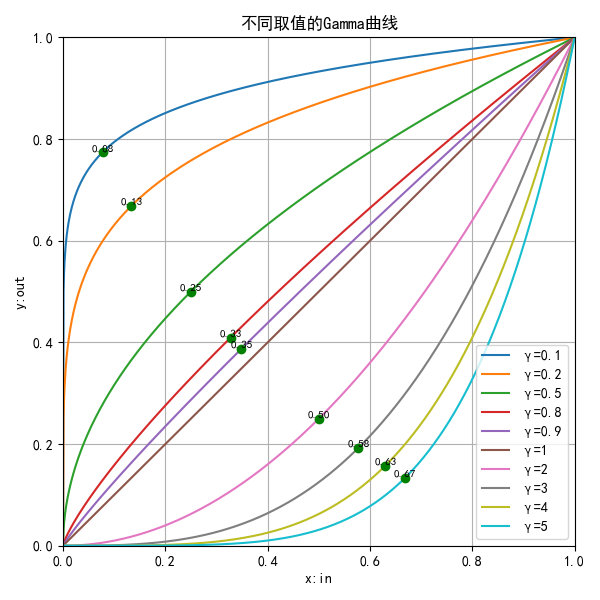
观察上图，有以下一些结论：

$\gamma =1$ 的曲线为恒等变换，即 $y=x$ ，经过该曲线（直线）变换后图像灰度保持不变。
当 $0<\gamma <1$ 时，曲线有如下性质：

变换曲线提升了图像整体亮度，因为对于 $[0,1]$ 区间的任意输入值x，均满足 $y(x)\geqslant x$ 。
在 $x\rightarrow +0$ 处，其一阶导数为 $+\infty$ ；在 $x\rightarrow 1$ 时，其一阶导数为0。
任意一条曲线都存在一个位于 $[0,1]$ 区间的点，在该点上曲线的导数为1（在每条曲线上均使用绿色圆点标注）；如在 $\gamma=0.5$ 曲线上，在点 $x=0.25$ 该曲线的导数为1。
导数为1的点对Gamma曲线进行分割，使得小于该点的灰度区间被拉伸(即图像暗部被拉伸)，其拉伸比接近该点处Gamma函数的因变量与自变量的比值，如 $\frac{y(x=0.25)}{0.25}$ 。
如果已知想要拉伸的暗部区域的大致范围，就可以选择对应的Gamma曲线进行拉伸。一般情况下，暗部区域亮度越低，就需要选择越低的Gamma曲线进行拉伸。

当 $\gamma > 1$ 时，变换曲线使得图像亮部得到拉伸，曲线性质与 $0<\gamma<1$ 相反，如下：

变换曲线降低了整体亮度，因为对于 $[0,1]$ 区间的任意输入值x，均满足 $y(x)\leqslant x$ 。
在 $x\rightarrow +0$ 处，其一阶导数为0；在 $x\rightarrow 1$ 时，其一阶导数为 $+\infty$ 。
导数为1的点对Gamma曲线分割，使得大于该点的灰度区间被拉伸（即图像亮部被拉伸），其拉伸比为 $\frac{1-y}{1-x}$ 。

使用Gamma增强图像

案例一：

上图是左边一张曝光不足的风景照，根据右边的直方图分析可知：其灰度区间主要集中在 $[10,20]$ 范围，用归一化区间表示为 $[0.04,0.08]$ ，这是一个非常窄的一个波峰。此时我们增加图像的目标如下：

提升整体图像亮度
拉伸暗部区域，使其具有更高的对比度
避免提升整体亮度时导致天空区域过曝

根据Gamma曲线性质， $0<\gamma < 1$ 的曲线正好同时以上要求。现在需要确定的是具体哪个gamma值表现最优，我们可以一个平均亮度目标来确定最佳 $\gamma$ 值，具体如下：

$\gamma_{expect}=\frac{ln^{I_{expect}}}{ln^{I_{real}}}$ ，即期望 $\gamma$ 由图像目标平均亮度与真实平均亮度的自然对数比确定，切记，这里的平均亮度需要做归一化处理。如目标亮度为100，真实亮度为30，则有： $\gamma_{expect}=\frac{ln^{(100/255)}}{ln^{(30/255)}}=0.437$ 。根据以上原则，该图像最后计算出的期望 $\gamma$ 约为0.55，应用Gamma变换得到以下结果：

通过Gamma变换：我们提升了整体图像亮度（上图右边亮度高于左边）；拉伸了山体部分的灰度区间，从而呈现出更多的细节；在天空部分，我们并没有因为提升亮度操作而过度曝光高亮区域。总体来说，我们得到了一张视觉效果更好的风景照。

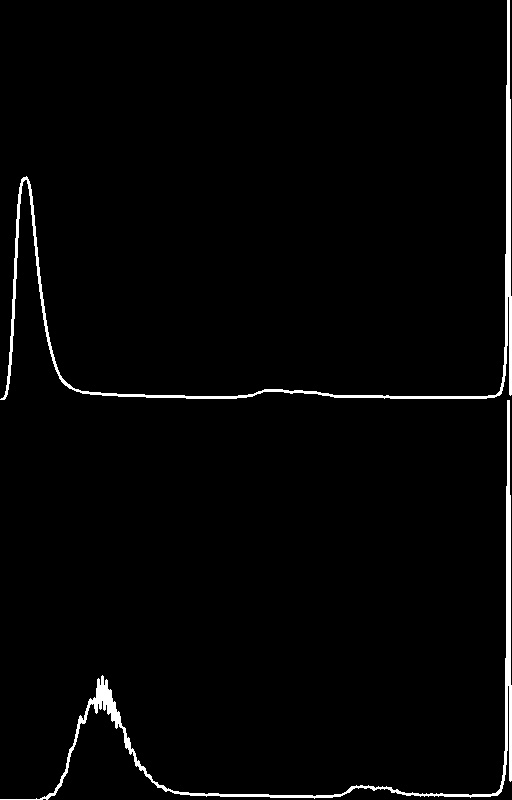
从以上直方图可以看出：变换后图像亮度得到了提升，且暗部灰度区间宽度更宽（拉伸了暗部），同时基本保持高亮区间不变。从直方图上进一步印证了我们的结论。

案例二：

上图左边是一张曝光过度的风景照，风景照的平均亮度约为165。观察直方图发现，相对于案例一中曝光不足风景照的直方图，该直方图的灰度分布区间很广（即对比度较高），但视觉效果看起来确有些雾蒙蒙的感觉。其实，这正是我们之前所说的人眼视觉的特性引起：人眼的视觉系统对低亮度比高亮度更敏感，我们能在黑暗中分辨出非常微小的亮度差异，但在高亮区域的感知能力却较弱，因此尽管直方图数据看来对比度较好，但人眼视觉感受确不太理想。

因此，我们在此处的调节重点是降低图像平均亮度，使其更加容易被人眼视觉感知。同时，我们也应该尽可能保持直方图的宽度，或者稍微扩张一下直方图的宽度以获得更佳的效果。

根据Gamma曲线的性质， $\gamma >1$ 的曲线满足降低亮度的要求，同时对高亮区域的对比度也有一定程度的拉伸。对应具体的gamma值的确定，我们可以利用之前的公式 $\gamma_{expect}=\frac{ln^{I_{expect}}}{ln^{I_{real}}}$ 来确定。我们仍旧设定目标亮度为100，其平均亮度为165，最终gamma值为2.1。有如下效果：

通过Gamma变换：我们降低了整体图像亮度，使其更容易被人眼视觉分辨；同时，对主要灰度区间进行了一定程度拉伸，提升了一定程度对比度。通过以上两种因素叠加，得到了一张视觉效果更好的风景照。

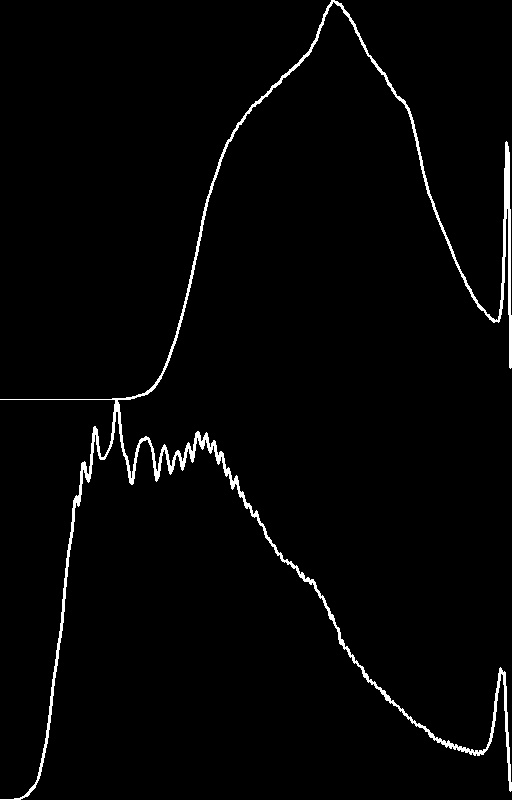
通过以上直方图对比，我们确实通过Gamma变换降低了图像平均亮度，使其更适合人眼视觉系统。在灰度对比度上，也有一定程度的提升。从直方图上进一步印证了我们的结论。

Gamma变换源码

void GammaAdjust(cv::Mat& imgSource, cv::Mat& imgDst, double gamma)
{
	// 确保图像位深为8为，如CV_8UC1, CV_8UC3, CV_8UC(n)
	int depth_src = imgSource.depth();
	int depth_dst = imgDst.depth();
	if (depth_src != CV_8U || depth_src != depth_dst)
		return;

	// 准备查找表
	// 由于Gamma变换涉及pow()函数，需要大量的计算，使用查找表可提升运行速度
	cv::Mat gammaLut(1, 256, CV_8U);
	uchar* gammaData = gammaLut.ptr();

	double dMax = pow(255., gamma);
	for (int i = 0; i < 256; ++i)
	{
		int m = (int)(pow((double)i, gamma) * 255. / dMax);
		if (m > 255) m = 255;
		if (m < 0)   m = 0;
		gammaData[i] = m;
	}

	// 应用查找表进行Gamma变换
	cv::LUT(imgSource, gammaLut, imgDst);
}

int main()
{
	cv::Mat img_src = cv::imread("src.jpg", cv::IMREAD_COLOR);
	if (img_src.empty()) return 0;  

	cv::Mat img_dst = cv::Mat::zeros(img_src.size(), img_src.type());

	GammaAdjust(img_src, img_dst, .55);

	cv::imwrite("1_src.jpg", img_src);
	cv::imwrite("2_dst.jpg", img_dst);

	return 0;
}

以上代码实现了Gamma变换，通过改变GammaAdjust函数的gamma参数值，可以达到预期的目标。我们注意到Gamma变换涉及pow运算，该运算在运行效率上很低（计算机最擅长做加法与乘法运算，这是线性变换的基本操作）。为了提升运行效率，我们使用查找表提前计算 $[0,255]$ 区间上每个整数点对应的Gamma变换结果，然后再后续操作中仅进行查表操作即可，这大幅提升了运行效率。

改进Gamma变换源码

到目前为止，我们基本讲清楚了Gamma变换在图像增强上的应用的所有内容，从数学原理到应用效果与完整源码。然而，还有一点值得我们去思考：在图像处理流水线(pipeline)中，我们一般使用浮点存储图像数据点，这样可以避免整个处理过程中的截断误差。如浮点数5.345被保存为整数时截断为5，在整个流水线中经过多次截断则会产生累积误差，使得图像质量变差。

所以，在很多情况下，我们应该使用浮点进行数据运算。但是，对于Gamma变换来说，如果使用浮点则无法利用查找表进行提速，使得Gamma变换效率大幅下降。在多数实时运算情况下，这也是不可接受的。

因此，我们提出两种改进方案，改进方案继续使用查找表以保证运行效率，同使通过一些差值等手段提升查找精度，如下：

方案一：

将[0,255]映射到[0,2047]，提升查找表的密度，即查找步长从1下降到0.125，以提升浮点查找精度。
使用线性加权方式提升落在查找表区间内的输入值的查找精度。

// 高效的浮点Gamma变换：提升查找表密度与线性加权
void GammaAdjustLinear(cv::Mat& imgSource, cv::Mat& imgDst, double gamma)
{
	int depth_src = imgSource.depth();
	int depth_dst = imgDst.depth();
	if (depth_src != CV_32F || depth_src != depth_dst)
		return;

	// 将[0,255]映射到[0,2047]，提升查找表的密度，
	// 即查找步长从1下降到0.125，以提升浮点查找精度
	cv::Mat gammaLut(1, 2048, CV_32F);
	float* gammaData = gammaLut.ptr<float>(0);

	// step = 8, idx 15 -> 15 / 8
	for (int i = 0; i < 2048; ++i)
	{
		float x = i / 2047.f;
		float y = powf(x, gamma) * 255.f;
		gammaData[i] = y;
	}

	// 利用多核提升运行效率
#pragma omp parallel for
	for (int row = 0; row < imgSource.rows; ++row)
	{
		float* datasrc = imgSource.ptr<float>(row);
		float* datadst = imgDst.ptr<float>(row);
		for (int col = 0; col < imgSource.cols * imgSource.channels(); ++col)
		{
			float srcVal = datasrc[col] * 8.f;
			int idx = static_cast<int>(srcVal);
			float ratio2 = srcVal - idx;
			float lut1 = gammaData[idx];
			float lut2 = gammaData[idx + 1];

			// 当输入值没有准确落在一个确定的查找值上，即落在两个查找值中间，
			// 使用线性加权的方式提升精度
			float lut = lut1 * (1.f - ratio2) + lut2 * ratio2;

			datadst[col] = lut;
		}
	}
}

方案二：

基于方案一，我们通过线性加权得到的查找值总会与真实值有一个误差，可以进一步改进。通过二阶线性近似： $f(x)=f(x_{0}) + f^{'}(x_{0})(x - x{0}) + \frac{1}{2}f^{''}(x_{0})(x - x{0})^{2}$ 可得到更好的结果。

$x$ 为需要计算Gamma变换的输入值
$x_{0}$ 为小于或等于 $x$ 且离 $x$ 最近的可通过查表获得Gamma变换的值
$f(x_{0})$ 为 $x_{0}$ 的真实Gamma变换值，他可以通过查找表获得
同样， $f^{'}(x_{0}),f^{''}(x_{0})$ 为 $x_{0}$ 上的一阶与二阶导数值，他们也可以通过查找表获得

通过以上已知调节，我们可以计算出 $f(x)$ 的估算值，该估算值与真实值误差约为： $\frac{1}{3!}f^{'''}(x_{0})(x-x_{0})^{3}$ 。很显然，3阶误差基本接近0，我们可以通过二阶近似得到一个较好的估计值。

// 使用二阶近似计算Gamma变换值
void GammaAdjustSecondApprox(cv::Mat& imgSource, cv::Mat& imgDst, double gamma)
{
	int depth_src = imgSource.depth();
	int depth_dst = imgDst.depth();
	if (depth_src != CV_32F || depth_src != depth_dst)
		return;

	// 将[0,255]映射到[0,2047]，提升查找表的密度，
	// 即查找步长从1下降到0.125，以提升浮点查找精度
	cv::Mat gammaLut(1, 2048, CV_32FC3);
	float* gammaData = gammaLut.ptr<float>(0);

	// step = 8, idx 15 -> 15 / 8
	for (int i = 0; i < 2048; ++i)
	{
		float x = i / 2047.f;
		float y0 = powf(x, gamma) * 255.f;
		float y1 = powf(x, gamma - 1.) * gamma;
		float y2 = powf(x, gamma - 2.) * gamma * (gamma - 1.);
		gammaData[i * 3] = y0;   // x点上的Gamma值
		gammaData[i * 3 + 1] = y1;   // x点上的一阶导数
		gammaData[i * 3 + 2] = y2;   // x点上的二阶导数
	}

	// 利用多核提升运行效率
#pragma omp parallel for
	for (int row = 0; row < imgSource.rows; ++row)
	{
		float* datasrc = imgSource.ptr<float>(row);
		float* datadst = imgDst.ptr<float>(row);
		for (int col = 0; col < imgSource.cols * imgSource.channels(); ++col)
		{
			float x = datasrc[col];
			int idx = static_cast<int>(x * 8.f);
			float y0 = gammaData[idx * 3];
			float y1 = gammaData[idx * 3 + 1];
			float y2 = gammaData[idx * 3 + 2];
			float x0 = idx * 0.125;
			float dx = x - x0;
			float dx2 = dx * dx;

			// 利用二阶近似计算真实Gamma变换值
			float val = y0 + y1 * dx + y2 * dx2 * .5;
			
			datadst[col] = val;
		}
	}
}

理解显示器的Gamma变换

显示器的Gamma曲线与sRGB格式的Gamma曲线为一对互逆的操作。之所以这么做主要有以下原因：

在保存图像文件时，我们使用了8位位深数据，其取值范围为 $[0,255]$ 。因此，我们必然对图像进行量化处理，从而降低了图像表达精度，如5.2，5.3的图像亮度值均被表达为5。
那么在8位位深条件下，我们应该怎样使得人眼能够观察到更好的图像效果呢？这就需要利用人眼视觉系统的特点进行优化。
人眼视觉系统对暗区敏感程度远高于亮区；如果我们在为8位位深图像时使用尽量多的数据表达暗区细节，而忽略一些亮区的细节，这样更加有利于人眼视觉系统的观察。因此，我们通过Gamma=0.45对原始图像进行变换，拉伸了暗区，压缩了亮区，这样就保存了更多的暗区细节。这就是sRGB格式中Gamma变换的作用。
在图像显示环节，我们使用Gamma=2.2的曲线将sRGB图像进行逆操作，还原了图像数据的线性关系。同使由于显示系统可以表达更精细的亮度，如可以区分显示5.2，5.3等亮度，人眼就可以观察到暗区部分更加精细的的变化。
对于亮区部分，由于之前保存sRGB图像时压缩了数据范围，还原后在显示器上的表达精度有所下降，如200，202，205等出现一些不连续性，但人眼视觉系统难以感知亮区的不连续性，看起来似乎并没有影响亮区的视觉效果。

以上就构成了显示系统中的Gamma变换的基本逻辑，其核心点就是在数据位深有限的情况下（8位位深），构造出更加符合人眼视觉特性的存储和显示系统。然而，这种为了迎合人眼视觉系统的改进可能不利于我们的计算机进行相关的图像处理操作。比如在卷积，HDR等一些线性运算中，我们应该确保图像数据是线性的，这样才能确保最终结果的准确性，后续我们在合适的时候对该问题展开讨论。

总结

本文系统介绍了Gamma变换在图像处理中的应用。文章首先通过夜景照片示例说明Gamma变换的必要性，详细推导了数学公式及导数性质，展示了不同参数下的曲线特征。在应用方面，通过两个典型案例（曝光不足和过度的风景照）演示了Gamma变换如何有效调节亮度和对比度，并给出完整的C++实现代码及优化方案。最后，文章解释了显示器Gamma校正的原理，说明其在有限位深条件下如何优化图像存储和显示。总之，Gamma变换在图像增强、编码压缩和显示优化中都具有重要作用。

系列链接

图像增强基础：直方图均衡化与自适应直方图均衡化

图像极坐标变换及超声图像上的应用

解析图像几何变换：从欧式到仿射再到透视

深入理解图像插值：从原理到应用

Gamma 变换详解：图像增强与显示系统的应用

RGB下的色彩变换:用线性代数解构色彩世界

从RGB到HSI：深入理解色彩空间

基于 OpenCV 的图像亮度、对比度与锐度调节

数字图像处理与OpenCV初探

魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

【计算机视觉】Pixel逐像素分类&Mask掩码分类理解摘要

魔乐社区

计算机视觉（opencv）实战三十二——CascadeClassifier 人脸微笑检测（摄像头）

本文从原理到实现，详细介绍了基于 OpenCV Haar 分类器的人脸与微笑检测：讲解了 Haar 特征和级联检测原理。对代码逐行拆解并解释参数含义。画出完整流程图，帮助理解执行过程。给出了常见问题和优化建议，甚至扩展到深度学习方法。这种方法简单、轻量、实时性好，非常适合入门和小型应用项目。但如果需要更高准确率和更强鲁棒性，建议使用深度学习检测器替代 Haar 分类器。