信息与通信的数学基础——第一次实验(1)
题目1:计算出下列复数的实部,虚部,模和幅角(1)1+i√31+i\surd 31+i√3
·
1. 计算出下列复数的实部,虚部,模和幅角
(1) 1 + i 3 1+i\sqrt{3} 1+i3
x = 1 + I*Sqrt[3]
Re[x]
Im[x]
Abs[x]
Arg[x]
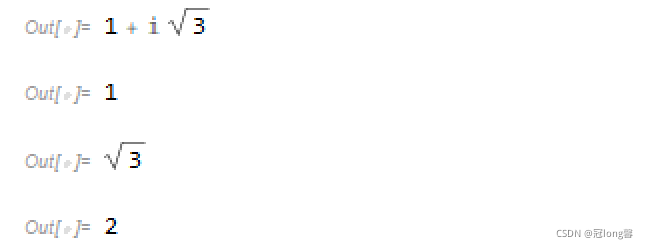
(2) 1 − c o s α + i s i n α , 0 ≤ α < 2 π 1-cos\alpha+isin\alpha, 0 \leq \alpha < 2\pi 1−cosα+isinα,0≤α<2π
f = Refine[1 - Cos[a] + I*Sin[a], 0 <= a < 2*Pi]
Refine[Re[f], 0 <= a < 2*Pi]
Refine[Im[f], 0 <= a < 2*Pi]
Refine[Norm[f], 0 <= a < 2*Pi]
Refine[ArcTan[f], 0 <= a < 2*Pi]
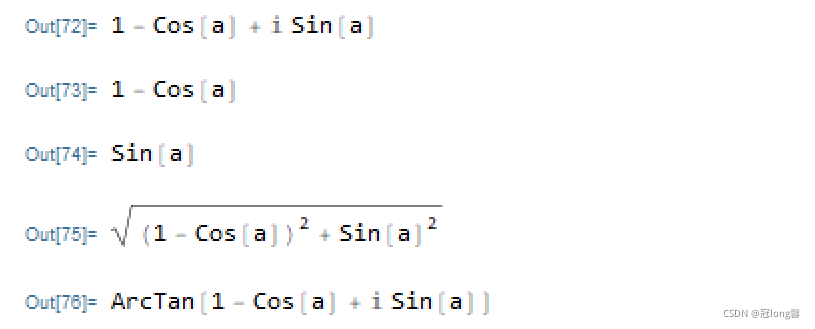
(3) e i s i n x , x 为 实 数 e^{isinx},x为实数 eisinx,x为实数
f = Refine[E^{I*Sin[x]}, x \[Element] Reals]
ComplexExpand[Re[f]]
ComplexExpand[Im[f]]
ComplexExpand[Abs[f]]
ComplexExpand[Arg[f]]
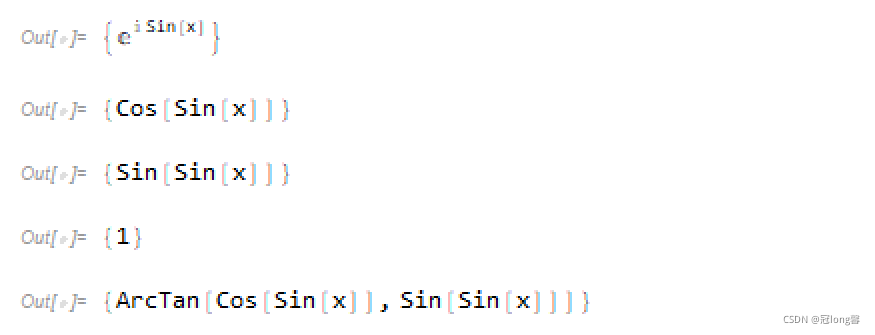
(4) e i z e^{iz} eiz
Clear[z];
f = E^{I*z}
ComplexExpand[Re[f], z]
ComplexExpand[Im[f], z]
ComplexExpand[Abs[f], z]
ComplexExpand[Arg[f], z]

2. 计算以上复数的和、差、积、商(任意组合、各两个)
f1 = 1 + I*Sqrt[3]
f2 = Refine[1 - Cos[a] + I*Sin[a], 0 <= a < 2*Pi]
f3 = ComplexExpand[E^{I*Sin[x]}]
f4 = E^{I*z}
ComplexExpand[f1 + f2]
ComplexExpand[f3 + f4, z]
ComplexExpand[f1 - f2]
ComplexExpand[f3 - f4, z]
ComplexExpand[f1 * f2]
ComplexExpand[f3 * f4, z]
ComplexExpand[f1 / f2]
ComplexExpand[f3 / f4, z]
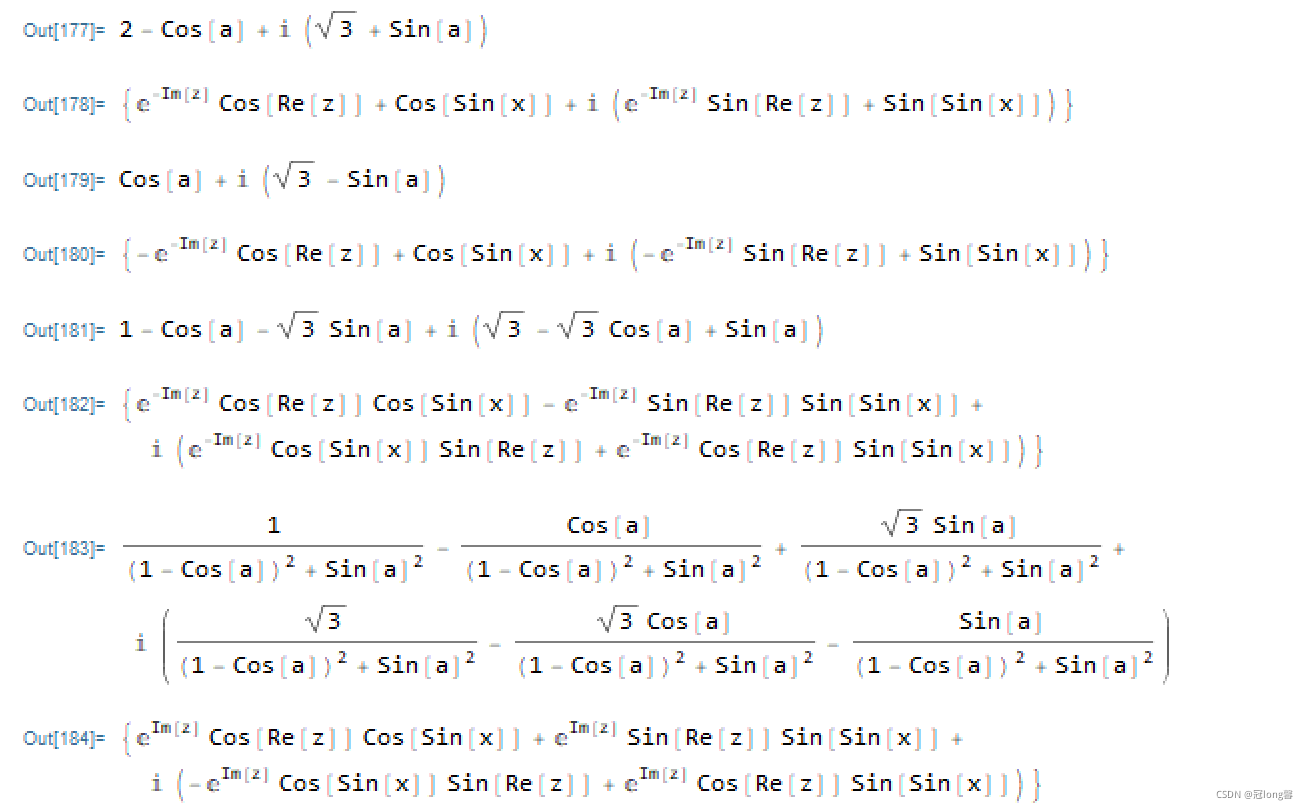
3. 计算下列复数方程的解,并画出它们的位置
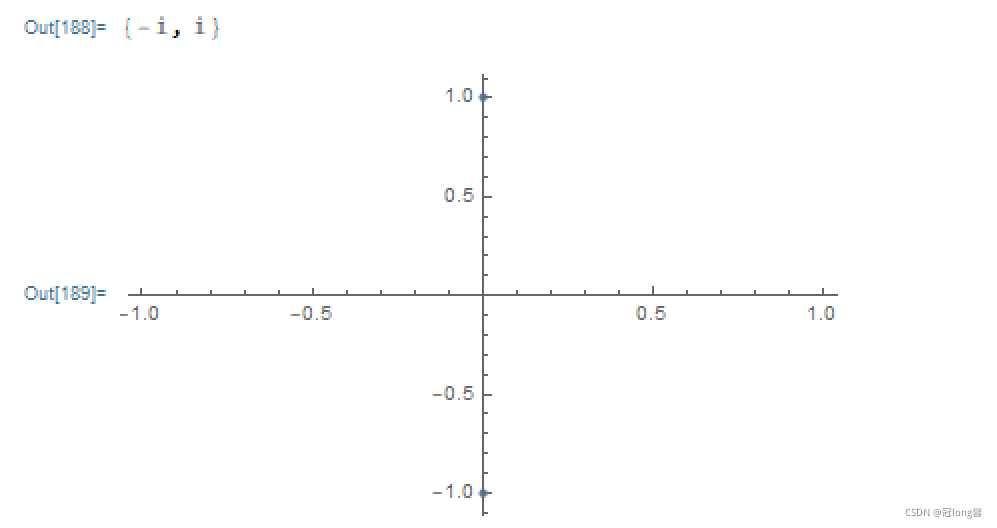
(1) z 2 + 1 = 0 z^2+1=0 z2+1=0
Solve[z^2 + 1 == 0, z];
temp1 = z /. {{z -> -I}, {z -> I}}
ListPlot[(Tooltip[{Re[#1], Im[#1]}] &) /@ temp1]
(2) z 3 + 8 = 0 z^3+8=0 z3+8=0
sol2 = Solve[z^3 + 8 == 0, z];
temp2 = z /. sol2
ListPlot[(Tooltip[{Re[#1], Im[#1]}] &) /@ temp2]
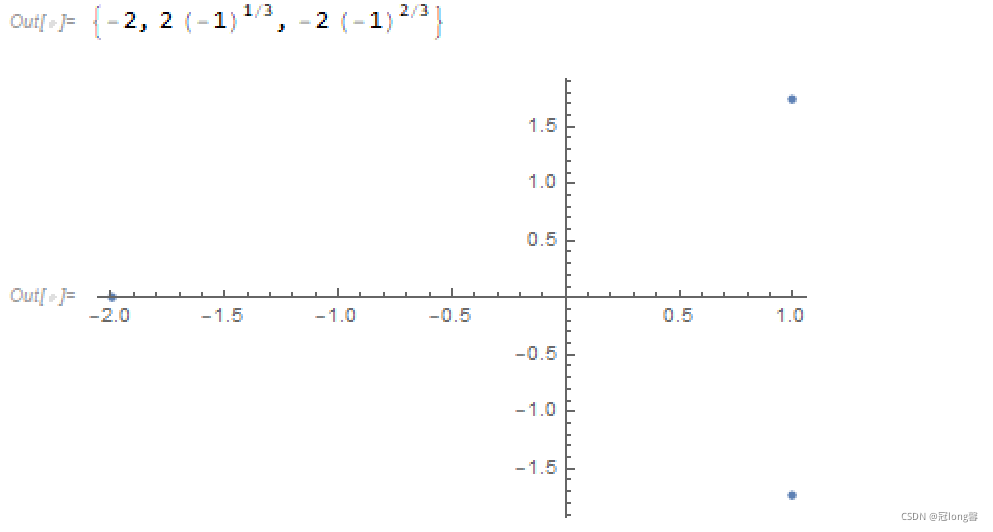
(3) z 4 − 1 = 0 z^4-1=0 z4−1=0
sol3 = Solve[z^4 - 1 == 0, z];
temp3 = z /. sol3
ListPlot[(Tooltip[{Re[#1], Im[#1]}] &) /@ temp3]
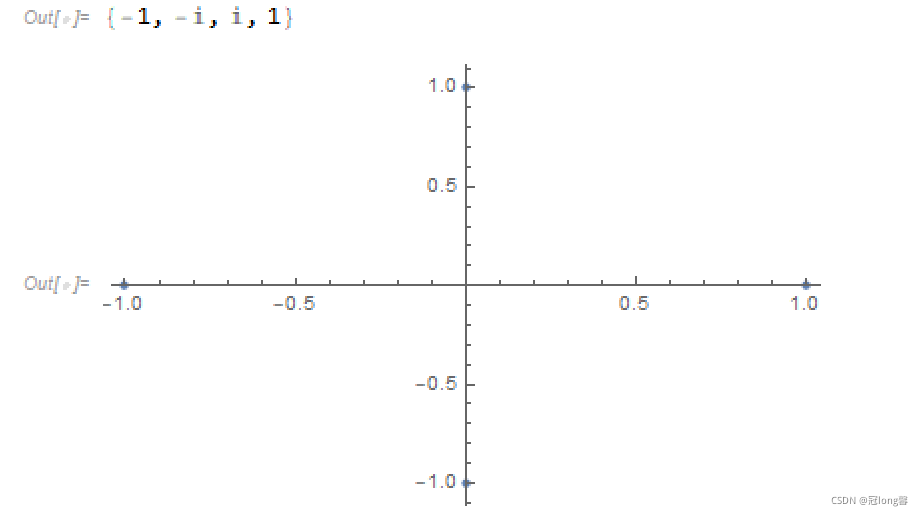
(4) z 4 + 1 = 0 z^4+1=0 z4+1=0
sol4 = Solve[z^4 + 1 == 0, z];
temp4 = z /. sol4
ListPlot[(Tooltip[{Re[#1], Im[#1]}] &) /@ temp4]
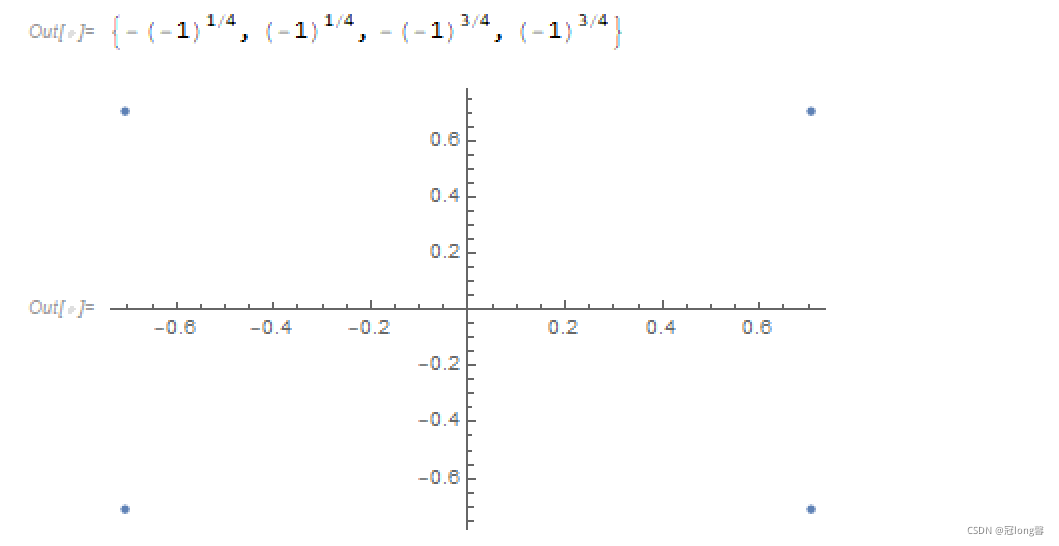
(5) z 2 n + 1 = 0 z^{2n}+1=0 z2n+1=0
i = 1;
temp5 = {};
While[i < 10, sol5 = Solve[z^{2*i} + 1 == 0, z]; p = z /. sol5;
temp5 = Join[temp5, p]; i++]
Print[temp5]
ListPlot[(Tooltip[{Re[#1], Im[#1]}] &) /@ temp5]
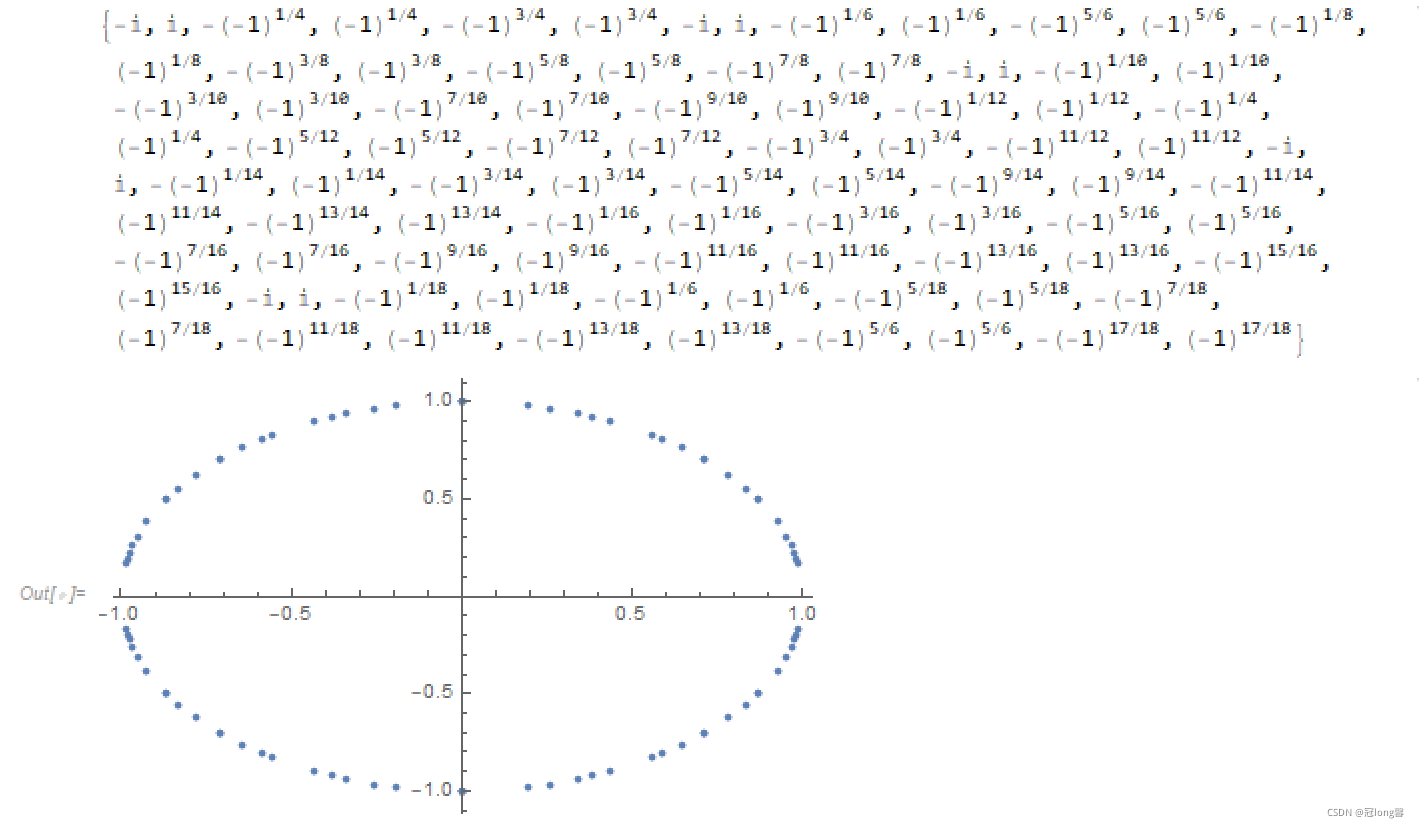
4. 把下列关系用几何图形表示出来
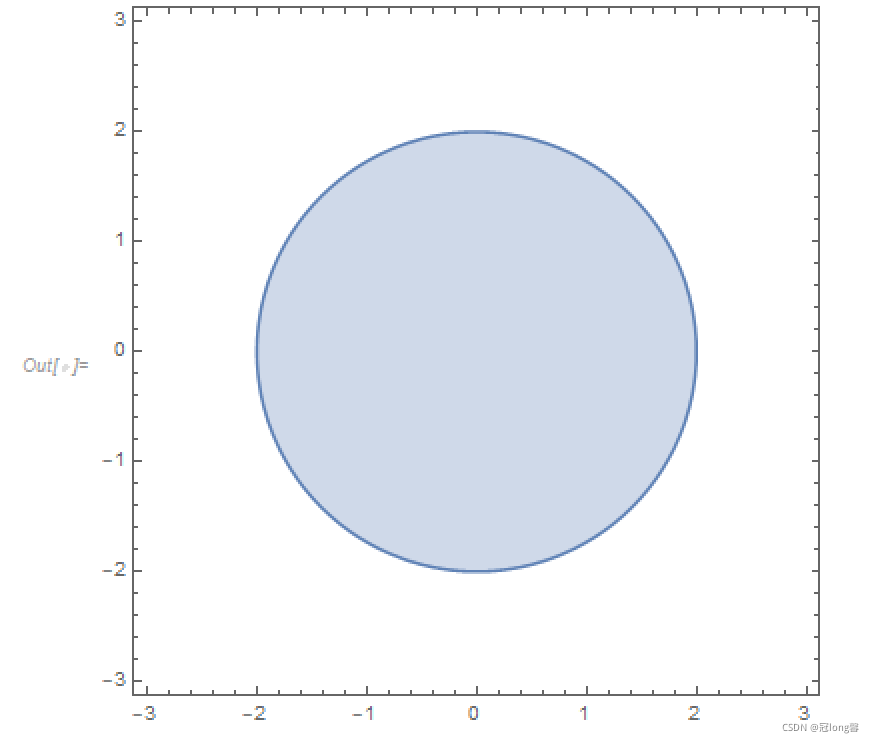
(1) ∣ z ∣ < 2 , ∣ z ∣ = 2 , ∣ z ∣ > 2 |z| <2, |z| =2,|z|>2 ∣z∣<2,∣z∣=2,∣z∣>2
RegionPlot[x^2 + y^2 < 4, {x, -3, 3}, {y, -3, 3}]
ContourPlot[x^2 + y^2 == 4, {x, -3, 3}, {y, -3, 3}]
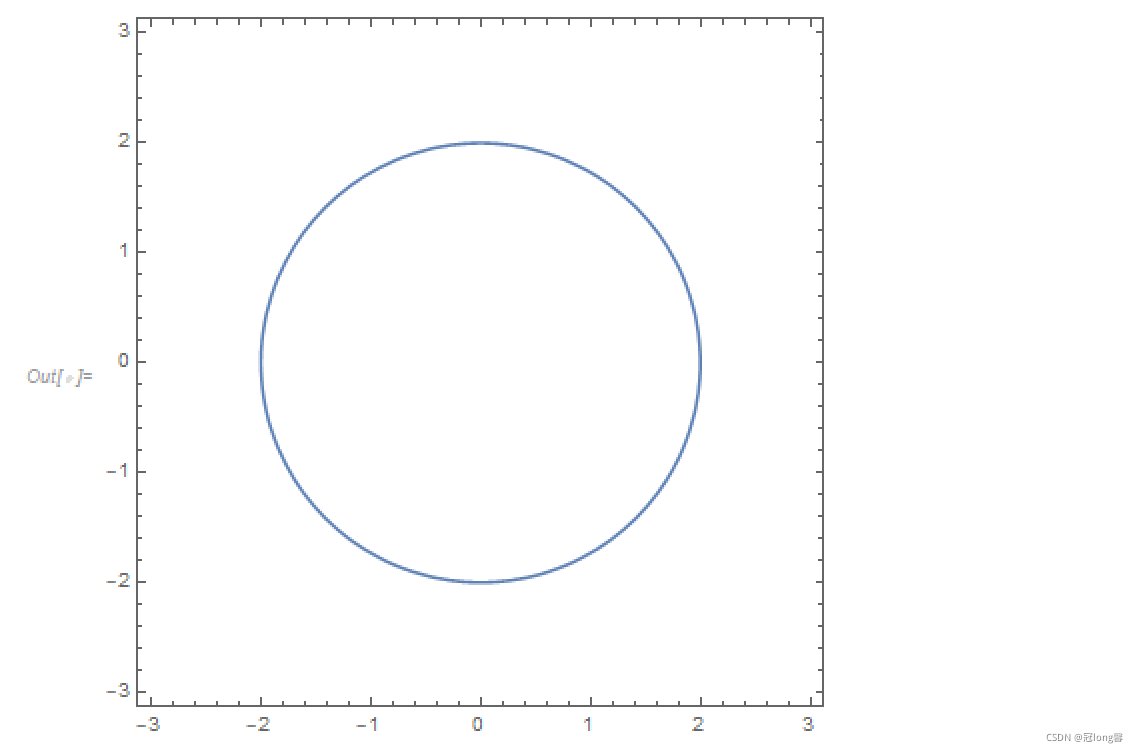
RegionPlot[x^2 + y^2 > 4, {x, -3, 3}, {y, -3, 3}]

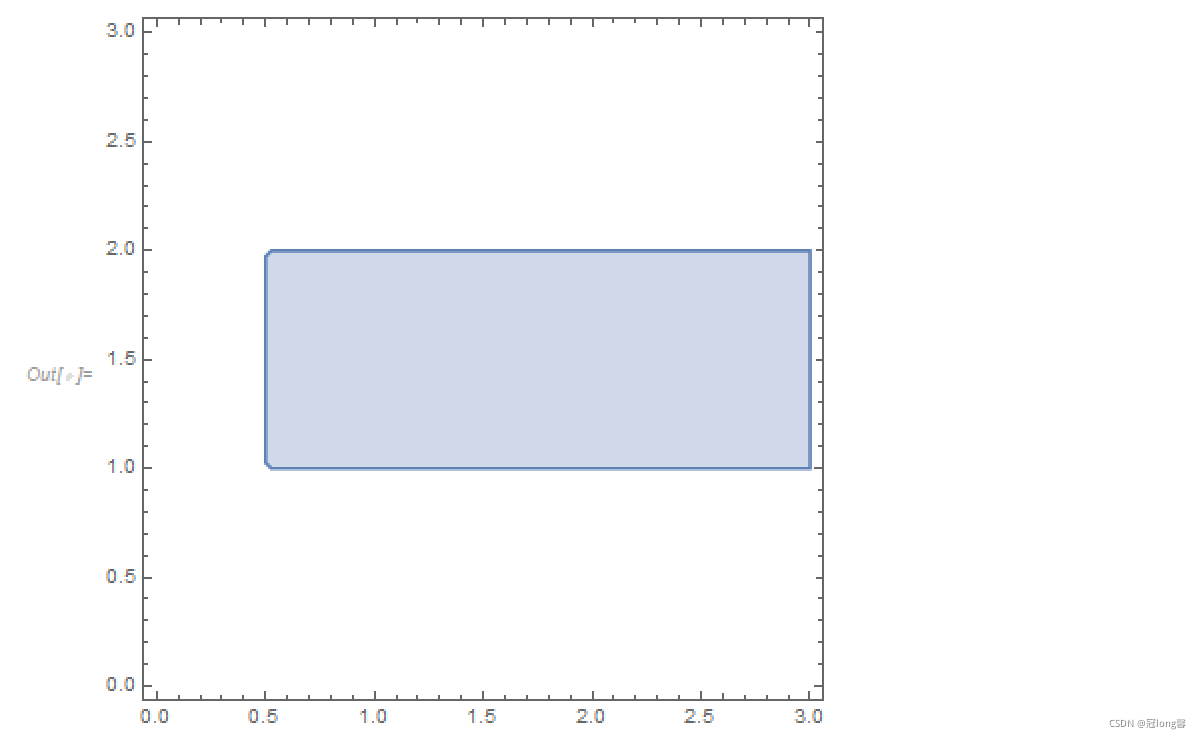
(2) R e z > 1 2 , 1 < I m z < 2 Rez > \frac{1}{2},1<Imz<2 Rez>21,1<Imz<2
RegionPlot[x > 1/2 && 1 < y < 2, {x, 0, 3}, {y, 0, 3}]

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容







所有评论(0)