第8章 矩阵和线性变换

• 线性变换 重要的性质就是不包括平移，线性变换可以使用3x3矩阵表示，包含平移的叫做仿射变换
• 考虑一下3x3的矩阵到底可以变换什么？
• 变换一个物体的坐标和变换坐标系这两个其实是等价的
• 2D中的旋转围绕点旋转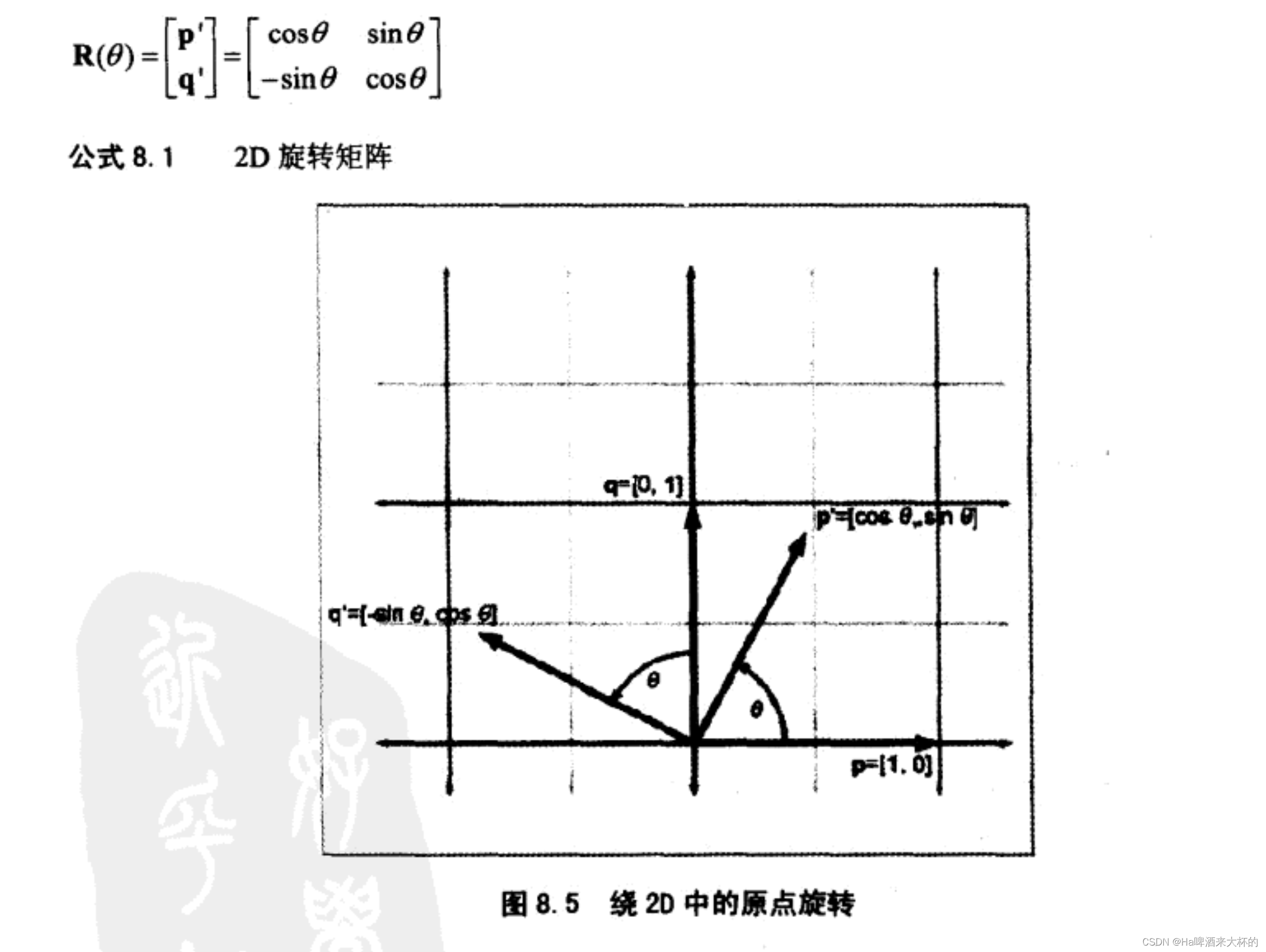
  
• 3D旋转 围绕轴旋转，可以由上面的2D延伸出来，假设z轴方向向里，那么其实上面的公式就是沿着z轴旋转，那么公式如下，并且绕x、y都可以由此推导出来
  

3D中任意轴旋转

• 上面的3D是按照标准轴旋转的，如何延伸出围绕任意轴旋转的矩阵呢？
  
• 上图是v向量绕n(单位向量)旋转，需要求出v’向量

1. 首先将向量v'分解为平行于n的向量v∥'，和垂直于n的向量v⟂' v∥平行于n所以不受影响，我们只要算出v⟂’就可以通过向量加法获得v’
2. v∥是v在n向量上的投影，根据之前学的投影公式可以算出来，进而根据向量减法得出v⟂
3. 辅助向量w，通过v⟂和n的叉乘算出，方向根据左手法则(向量首尾相连为顺时针)得知如图向上，w向量的长度v⟂和n向量组合成的平行四边形面积，因为n为单位向量，所以w和v⟂向量长度相同
4. 计算向量都有了，怎样表示v⟂' 向量，上面我们知道w和v⟂向量垂直并且长度相同，所以可以视为一个2维的坐标轴，那么v⟂'向量在这个坐标上，并且角度也知道，就可以根据2D的表示方式，如下公式(这个可以好好想一下，书上没有解释这个公式怎么来的)$$v{\perp }^{\prime }=v\perp cos\theta +wsin\theta$$
5. 最后只需要把步骤2、3的向量代入就可以计算出来v⟂'，然后根据向量加法算出v'，算出来很长一坨，就不写在这了，想看的去看书。

缩放

• 缩放分为均匀缩放和非均匀缩放
• 缩放将会导致变长、变短、正交投影、镜像
• 沿轴进行缩放的正好就是对角矩阵
  

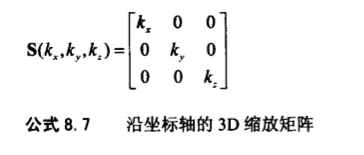
沿任意轴缩放

• 求v沿着n进行缩放

1. 首先将v分解为平行n的向量v∥和垂直于n的向量v⟂，根据2D缩放情况，垂直于缩放方向的向量不受缩放影响，所以需要算出v∥'，然后和v⟂向量加法就行
2. v∥' = kv∥，v∥就是投影可以根据投影公式求出，下面图是怎么根据v的等式求得变化矩阵
   

正交投影(平移投影)

• 向坐标轴或平面投影 下图可以看到这个矩阵会将z轴的长度变为0，xy轴的不变
  

向任意直线(轴)或平面投影

• 上面求沿任意轴缩放，那么只需要将缩放因子k=0就可以得到沿任意轴的投影，3D沿平面投影同理
  

镜像

• 沿直线或者平面进行翻折
• 上面求沿任意轴缩放，那么只需要将缩放因子k=-1就可以得到沿任意轴的投影，3D沿平面投影同理
  

切变

• 切变是一种坐标系扭曲变换，面积和体积保持不变，这个比较抽象看图吧
  
  上面的变换矩阵为
  
  上面那个矩阵比如拿[0,1]也就是y轴单位向量乘这个矩阵得到的向量就是[s, 1]，x轴单位向量[1,0]乘矩阵还是[1,0]
• 下面是3D的切变矩阵
  

变换的组合

首先带着疑问，有一个任意方向位置的物体，渲染到任意方向任意位置的摄像机中，怎么渲染？具体就是先将物体变换到世界坐标系，然后从世界坐标系变换到摄像机坐标系，公式如下

• 第7章得到的一个重要结论：矩阵的行向量就是矩阵变换后的基向量，可以看下图，并且可以单独以A的行向量于B相乘得到的就是B的行向量
  

变换的分类

• 线性变换的重要引理

1. 这个定义很像我们在操作矩阵基向量情况
   F(a) = aM M为任意方阵 a为向量
   F(a + b) = (a + b)M
   F(a + b) = aM + bM
   F(a + b) = F(a) + F(b)
2. F(ka) = kaM
   F(ka) = kF(a)
3. 零向量变换的结构仍然为零向量

• 仿射变换 是指进行线性变换然后进行平移，所以仿射变换是线性变换的超集，所有线性变换都是仿射变换，但是所有仿射变换不一定是线性变换 任何具有v' = vM + b形式的都是仿射变换
• 可逆变换 存在一个逆变换，可以取消原变换
  – 投影无法取消，投影放弃了某个维度的信息，无法复原，这个可以自己用矩阵乘一下
• 等角变换 如果两个向量变换后的角度不变则为等角变换，所有平移旋转和均匀缩放都是等角变换，镜像不是等角变换，因为方向发生了变化。
• 正交变换 的基本思想是轴保持互相垂直，并且不进行缩放变换，并且正交变换非常容易求出逆，平移、旋转、镜像是仅有的正交变换
• 刚体变换 只改变位置与方向，镜像不是刚体变换
• 下面是变换总结表