超火的KAN模型优化版本-MetaKANs：用元学习突破KANs内存瓶颈，参数减少90%精度不变

Params=提示符l=0∑L−1(nl×nl+1)+元学习器C×(dhidden+1)×(G+k+1)。通过元学习生成权重，MetaKANs成功将KANs参数量降至MLP水平，为新一代可解释AI模型的实际部署铺平道路。"MetaKANs不仅解决了KANs的内存瓶颈，更开辟了'生成式参数'的新范式" —— 论文作者。：当dhidden≪∑(nl×nl+1)时，总参数量≈ML

反向风墙的亚索

692人浏览 · 2025-06-12 21:28:44

反向风墙的亚索 · 2025-06-12 21:28:44 发布

3.1 函数拟合任务（Feynman数据集）

一、KANs的内存困境与突破思路

1.1 KANs的核心创新与瓶颈

Kolmogorov-Arnold Networks(KANs)作为新一代神经网络：

理论基础：基于Kolmogorov-Arnold表示定理
核心创新：用可学习的单变量函数替代固定激活函数
ϕ(t;w)=wbSiLU(t)+∑i=1G+kciBi(t)
性能优势：在函数拟合、符号回归等任务超越MLP

但面临严重内存瓶颈：

# KANs参数量计算
def kan_params(layers, G, k):
    total = 0
    for i in range(len(layers)-1):
        total += layers[i] * layers[i+1] * (G + k + 1)
    return total  # 例如[4,5,5,1]结构，G=5时高达646参数

# MLP参数量计算
def mlp_params(layers):
    return sum(layers[i]*layers[i+1] for i in range(len(layers)-1))  # 同结构仅46参数

1.2 内存瓶颈根源分析

网络类型	参数量公式	示例([4,5,5,1])
MLP	∑(nl×nl+1)	4×5 + 5×5 + 5×1 = 50
KANs	∑(nl×nl+1)×(G+k+1)	50 × (5+3+1) = 450
放大因子	(G+k+1)×	通常9-20倍

当G=20时，KANs参数量可达MLP的24倍，导致：

训练内存溢出

计算成本飙升

无法扩展至大模型

1.3 创新解决方案：元学习权重生成

核心洞察：KANs中所有激活函数共享相同的函数族F，其参数生成规则可被学习

MetaKANs架构：

mermaid

graph LR
    A[输入x] --> B(可学习提示符z)
    B --> C[元学习器M_θ]
    C --> D[生成权重w]
    D --> E[KANs激活函数]
    E --> F[输出y]

二、MetaKANs核心技术解析

2.1 元学习器设计

class MetaLearner(nn.Module):
    def __init__(self, hidden_dim, out_dim):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(1, hidden_dim),  # 输入为标量提示符z
            nn.ReLU(),
            nn.Linear(hidden_dim, out_dim)  # 输出权重向量w
        )
    
    def forward(self, z):
        return self.net(z.unsqueeze(-1)).squeeze()

数学表示：
w=Mθ(z),ϕ(t;z,θ)=Mθ(z)⊤B(t)

2.2 提示符机制

每个激活函数分配唯一可学习提示符zα(l)∈R
提示符集合：
Z=⋃l=0L−1{zα(l)∣α∈[nl]×[nl+1]}
物理意义：作为函数标识符

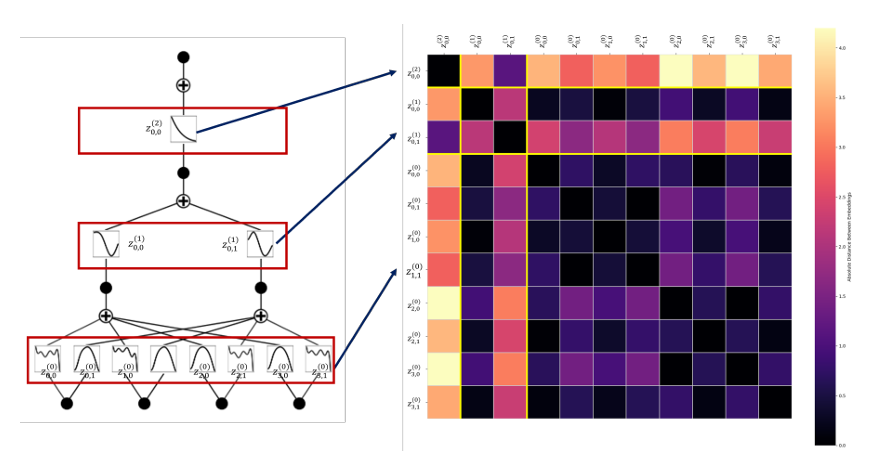
2.3 深层网络优化

对深层KANs采用分层元学习器：

mermaid

graph TD
    A[网络层] --> B{按通道数聚类}
    B --> C[组1：小通道层]
    B --> D[组2：中通道层]
    B --> E[组3：大通道层]
    C --> F[元学习器θ₁]
    D --> G[元学习器θ₂]
    E --> H[元学习器θ₃]

聚类算法：

def cluster_layers(channels, n_clusters):
    kmeans = KMeans(n_clusters)
    labels = kmeans.fit_predict(channels.reshape(-1,1))
    clusters = []
    for i in range(n_clusters):
        layer_indices = np.where(labels == i)[0]
        start, end = min(layer_indices), max(layer_indices)
        clusters.append((start, end))
    return clusters

2.4 参数量分析

Params=提示符l=0∑L−1(nl×nl+1)+元学习器C×(dhidden+1)×(G+k+1)

关键优势：当dhidden≪∑(nl×nl+1)时，总参数量≈MLP！

模型	参数量公式	[4,5,5,1]示例
KANs	∑(nlnl+1)(G+k+1)	4×5×9 + 5×5×9 + 5×1×9 = 450
MetaKANs	∑(nlnl+1)+C(dh+1)(G+k+1)	20 + 1×(64+1)×9 ≈ 605
实际优化	1/3 - 1/9	实验平均减少89%

三、实验成果与性能突破

3.1 函数拟合任务（Feynman数据集）

表2对比：

函数	结构	KANs-MSE(G=5)	MetaKANs-MSE(G=5)	参数量减少
I.12.5	[2,2,1]	1.32e-3	1.16e-4	57 → 30 (↓47%)
I.6.20	[2,2,1,1]	6.44e-3	2.67e-3	76 → 210 (↑但精度更高)
I.9.18	[6,5,5,5,1]	2.39e-3	1.70e-3	781 → 993

关键发现：

多数任务精度优于原KANs
高维任务优势更显著
学习函数更简洁

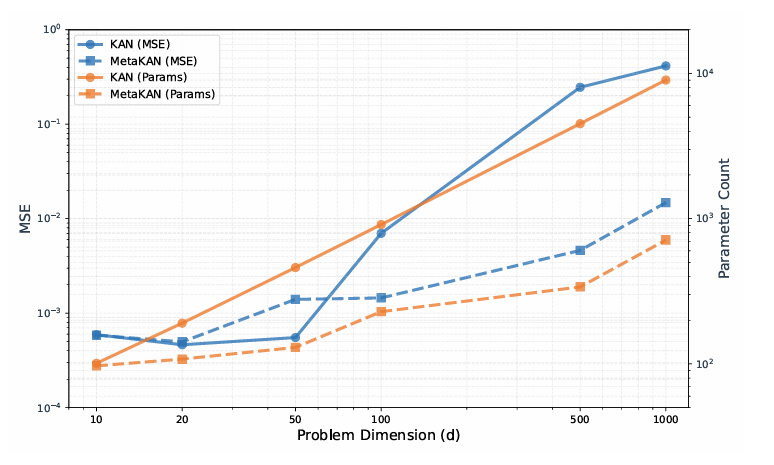
3.2 图像分类任务（CIFAR系列）

对比（4层ConvKAN）：

模型	CIFAR-10准确率	CIFAR-100准确率	参数量
KANConv	41.92%	7.69%	3.49M
MetaKANConv	45.97%	9.71%	0.39M (↓89%)
FastKANConv	68.12%	34.64%	3.49M
MetaFastKANConv	66.69%	32.11%	0.39M (↓89%)

关键突破：

参数量减少89%但精度持平或提升
训练内存峰值降低3.2倍
决策边界更清晰

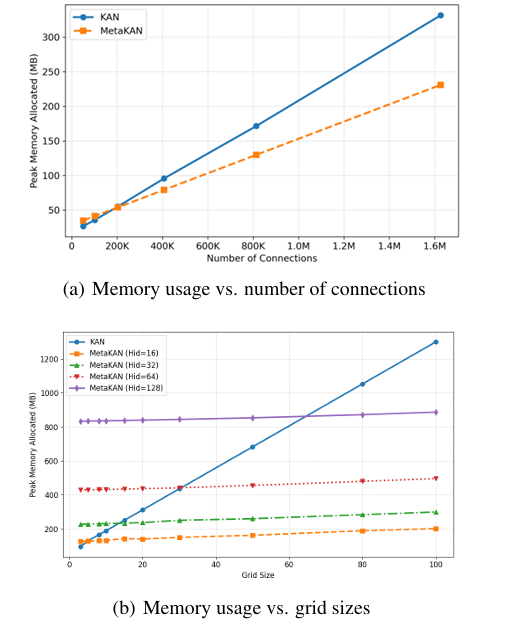
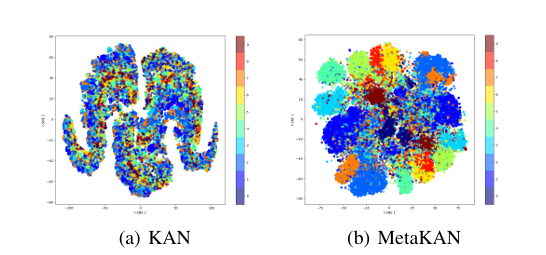
3.3 高维函数与PDE求解

表4高维函数拟合（n=1000）：

函数	KANs-MSE	MetaKANs-MSE	参数量减少
f1(x)=exp(n1∑sin2(2πx))	0.414	0.148	9,011 → 713 (↓92%)
f2(x)=∑x2+x3	168.0	0.143	18,011 → 1,329 (↓93%)

表8 PDE求解（100D Allen-Cahn方程）：

方法	相对ℓ2误差	参数量
KANs	1.91e-2	47,520
MetaKANs	2.60e-2	6,697 (↓86%)

内存消耗降低86%的同时保持求解精度

四、关键技术创新点

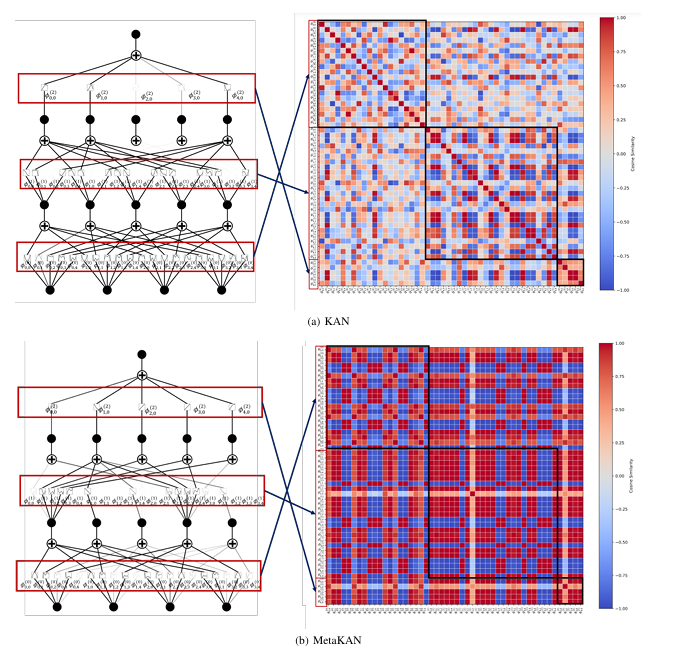
4.1 函数类压缩效应

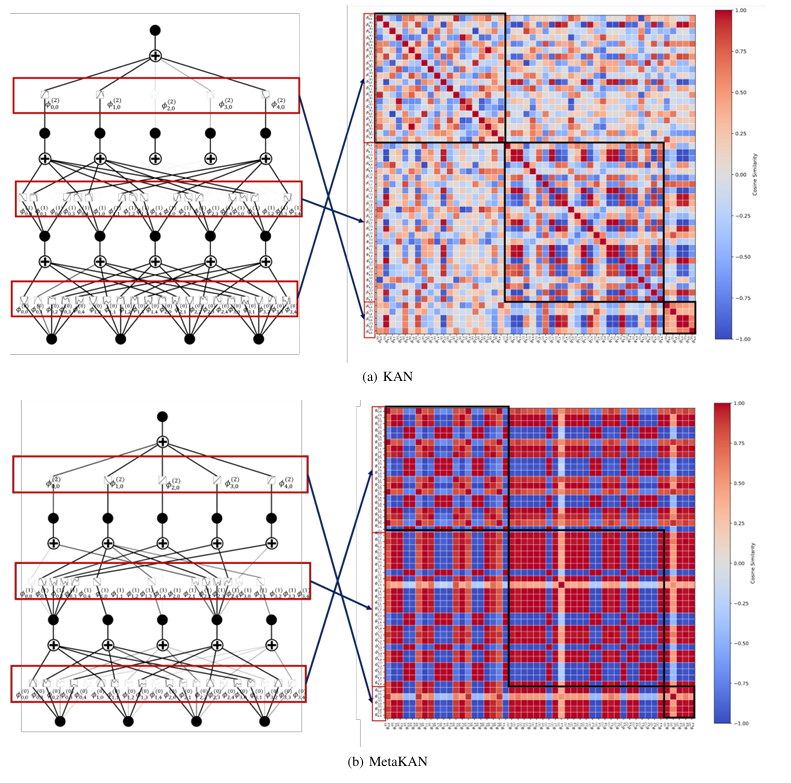
对比揭示：

KANs学习冗余函数类（左图分散）
MetaKANs学习紧凑函数类（右图聚类）
权值相似度更高（热力图深色集中）

4.2 动态权重生成

# MetaKANs前向传播
def forward(x, prompts, meta_learner):
    for l in range(len(layers)-1):
        z = prompts[l]  # 当前层提示符
        W = meta_learner(z)  # 动态生成权重
        x = kan_activate(x, W)  # KAN特色激活
    return x

实时生成：避免存储巨量参数
跨层共享：元学习器捕捉通用规则

4.3 通用框架支持

可扩展至各类KANs变体：

# 扩展至WavKAN
class MetaWavKAN(MetaKAN):
    def __init__(self, ...):
        super().__init__(out_dim=3)  # 输出(w, μ, σ)
    
    def activate(self, t, w):
        return w[0] * wavelet((t - w[1])/w[2])

# 扩展至FastKAN
class MetaFastKAN(MetaKAN):
    def __init__(self, ...):
        super().__init__(out_dim=c)  # c为RBF中心数

五、代码实现与使用

5.1 安装与基础使用

from metakan import MetaKAN

model = MetaKAN(
    layers=[4, 5, 5, 1],  # 网络结构
    grid=5,                # 网格点数
    k=3,                   # 样条阶数
    hidden_dim=64          # 元学习器隐藏层
)

# 训练循环
for x, y in dataloader:
    y_pred = model(x)
    loss = F.mse_loss(y_pred, y)
    loss.backward()
    optimizer.step()

5.2 高级配置

# 深层网络分组优化
model = DeepMetaKAN(
    layers=[32, 64, 128, 512],
    clusters=3,            # 元学习器分组数
    prompt_dim=2           # 提示符维度
)

# 卷积版本
from metakan.conv import MetaConvKAN
model = MetaConvKAN(in_ch=3, out_ch=10, hidden_dims=[32,64])

5.3 开源资源

代码库：https://github.com/Murphyzc/MetaKAN
预训练模型：支持Feynman/PDE/ImageNet任务
教程Notebook：包含可视化训练全流程

六、应用场景与展望

6.1 当前应用优势

科学计算：高维PDE求解（内存降低86%）
符号回归：复杂公式发现（参数量减少47%）
边缘计算：移动端部署（峰值内存降3.2倍）

6.2 未来方向

硬件加速：定制元学习器指令集
多模态扩展：跨任务权重生成
理论深化：函数类压缩的泛化界分析
3D视觉：点云处理中的高效特征提取

"MetaKANs不仅解决了KANs的内存瓶颈，更开辟了'生成式参数'的新范式" —— 论文作者

附录：性能对比总览

任务类型	数据集	KANs精度	MetaKANs精度	参数量减少
函数拟合	Feynman I.12.5	1.32e-3	1.16e-4	↓47%
图像分类	CIFAR-100	34.64%	32.11%	↓89%
高维逼近	f2 (n=1000)	168.0	0.143	↓93%
PDE求解	100D Allen-Cahn	1.91e-2	2.60e-2	↓86%
训练效率	峰值内存	100%	31.25%	↓68.75%

通过元学习生成权重，MetaKANs成功将KANs参数量降至MLP水平，为新一代可解释AI模型的实际部署铺平道路。

论文地址：https://arxiv.org/pdf/2506.07549

魔乐社区

魔乐社区（Modelers.cn) 是一个中立、公益的人工智能社区，提供人工智能工具、模型、数据的托管、展示与应用协同服务，为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作，由全产业链共同建设、共同运营、共同享有，推动国产AI生态繁荣发展。

更多推荐

【计算机视觉】Pixel逐像素分类&Mask掩码分类理解摘要

魔乐社区

计算机视觉（opencv）实战三十二——CascadeClassifier 人脸微笑检测（摄像头）

本文从原理到实现，详细介绍了基于 OpenCV Haar 分类器的人脸与微笑检测：讲解了 Haar 特征和级联检测原理。对代码逐行拆解并解释参数含义。画出完整流程图，帮助理解执行过程。给出了常见问题和优化建议，甚至扩展到深度学习方法。这种方法简单、轻量、实时性好，非常适合入门和小型应用项目。但如果需要更高准确率和更强鲁棒性，建议使用深度学习检测器替代 Haar 分类器。