【图形学数学基础】第一章
计算机图形学第一定律:只要看起来是对的,那么他就是对的。
计算机图形学第一定律:只要看起来是对的,那么他就是对的。
笛卡尔坐标系
弧度和角度的换算
360o = 2 π \pi π ,180o = π \pi π 所以
角度转弧度:乘π/180
弧度转角度:乘180/π
360是一个相对随意的选择,因为错用了一年365天的时间
三角函数恒等式
对称相关
s i n ( − θ ) = − s i n ( θ ) , c o s ( − θ ) = c o s ( θ ) , t a n ( − θ ) = − t a n ( θ ) sin(-\theta) = -sin(\theta),\quad cos(-\theta) =cos(\theta),\quad tan(-\theta) = -tan(\theta) sin(−θ)=−sin(θ),cos(−θ)=cos(θ),tan(−θ)=−tan(θ)
s i n ( π 2 − θ ) = c o s ( θ ) , c o s ( π 2 − θ ) = s i n ( θ ) , t a n ( π 2 − θ ) = − c o t ( θ ) sin(\frac{\pi}{2}-\theta) = cos(\theta),\quad cos(\frac{\pi}{2}-\theta) =sin(\theta),\quad tan(\frac{\pi}{2}-\theta) = -cot(\theta) sin(2π−θ)=cos(θ),cos(2π−θ)=sin(θ),tan(2π−θ)=−cot(θ)
毕达哥拉斯定理
a 2 + b 2 = c 2 a^2+b^2=c^2 a2+b2=c2
也叫勾股定理,两条直角边的平方和等于斜边的平方和。
毕达哥拉斯恒等式
s i n 2 θ + c o s 2 θ = 1 , 1 + t a n 2 θ = s e c 2 θ , 1 + c o t 2 θ = c s c 2 θ sin^2 \theta + cos^2 \theta = 1, \quad 1+tan^2 \theta = sec^2 \theta, \quad 1+cot^2 \theta = csc^2 \theta sin2θ+cos2θ=1,1+tan2θ=sec2θ,1+cot2θ=csc2θ
和差恒等式
s i n ( a + b ) = s i n ( a ) c o s ( b ) + c o s ( a ) s i n ( b ) , s i n ( a − b ) = s i n ( a ) c o s ( b ) − c o s ( a ) s i n ( b ) sin(a+b)=sin(a)cos(b) + cos(a)sin(b), \quad sin(a-b)=sin(a)cos(b) - cos(a)sin(b) sin(a+b)=sin(a)cos(b)+cos(a)sin(b),sin(a−b)=sin(a)cos(b)−cos(a)sin(b)
c o s ( a + b ) = c o s ( a ) c o s ( b ) − s i n ( a ) s i n ( b ) , c o s ( a + b ) = c o s ( a ) c o s ( b ) + s i n ( a ) s i n ( b ) cos(a+b) = cos(a)cos(b)-sin(a)sin(b),\quad cos(a+b) = cos(a)cos(b)+sin(a)sin(b) cos(a+b)=cos(a)cos(b)−sin(a)sin(b),cos(a+b)=cos(a)cos(b)+sin(a)sin(b)
t a n ( a + b ) = t a n ( a ) + t a n ( b ) 1 − t a n ( a ) t a n ( b ) , t a n ( a − b ) = t a n ( a ) − t a n ( b ) 1 + t a n ( a ) t a n ( b ) tan(a+b)=\frac{tan(a)+tan(b)}{1-tan(a)tan(b)},\quad tan(a-b) = \frac{tan(a)-tan(b)}{1+tan(a)tan(b)} tan(a+b)=1−tan(a)tan(b)tan(a)+tan(b),tan(a−b)=1+tan(a)tan(b)tan(a)−tan(b)
等腰三角形恒等式(a=b= θ \theta θ)
s i n ( 2 θ ) = 2 s i n ( θ ) c o s ( θ ) , t a n ( 2 θ ) = 2 t a n ( θ ) 1 − t a n 2 ( θ ) sin(2\theta) = 2sin(\theta)cos(\theta), \quad tan(2\theta)=\frac{2tan(\theta)}{1-tan^2(\theta)} sin(2θ)=2sin(θ)cos(θ),tan(2θ)=1−tan2(θ)2tan(θ)
c o s ( 2 θ ) = c o s 2 ( θ ) − s i n 2 ( θ ) = 2 c o s 2 ( θ ) − 1 = 1 − 2 s i n 2 ( θ ) cos(2\theta)=cos^2(\theta)-sin^2(\theta)=2cos^2(\theta)-1=1-2sin^2(\theta) cos(2θ)=cos2(θ)−sin2(θ)=2cos2(θ)−1=1−2sin2(θ)
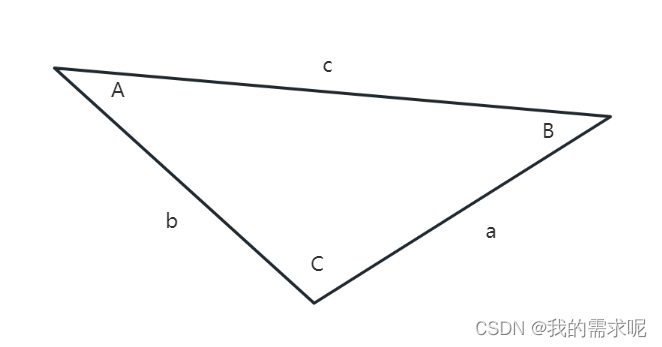
正弦定理
s i n A a = s i n B b = s i n C c \frac{sinA}{a} = \frac{sinB}{b} = \frac{sinC}{c} asinA=bsinB=csinC
余弦定理
a 2 = b 2 + c 2 − 2 b c ∗ c o s A , b 2 = a 2 + c 2 − 2 a c ∗ c o s B , c 2 = a 2 + b 2 − 2 a b ∗ c o s C . a^2 = b^2+c^2-2bc*cosA,\\ b^2 = a^2+c^2-2ac*cosB,\\ c^2=a^2+b^2-2ab*cosC. a2=b2+c2−2bc∗cosA,b2=a2+c2−2ac∗cosB,c2=a2+b2−2ab∗cosC.

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容







所有评论(0)