mini snap可以获得一个经过路径的点，但是可能会“超调”（在其他点触碰障碍）

主要有两种解决思路：软约束、硬约束；

软约束是将约束加在目标函数里，让目标远离边界条件。硬约束是要求全局满足。

一、硬约束

硬约束：飞行走廊；基本用凸的进行表示，比如方块。 

约束两段轨迹连接点在重叠的飞行走廊内，但是这并不能保障轨迹不跑出飞行走廊。只能通过后验性迭代检查进行约束，还有动力学约束。

一般是通过检查极值去重新迭代约束条件。四次以内用求根公式，四次以外用伴随矩阵的特征值，matlab里面函数名为root。

方法：贝塞尔曲线、找很多点和框、混合整数优化、

二、Bezier Curve Optimization

普通多项式可以通过矩阵M一一对应到贝赛尔曲线；

特点：

①只通过第一个和最后一个，不通过中间几个控制点。

②总是被外面的凸包所包围。由凸包定义的贝塞尔曲线一定被限制在凸包里面。

③求导后仍然是贝塞尔曲线，并可以用线性表示。

④贝塞尔曲线的时间都是定义在[0,1]上的。

好处是可以直接求解，不需要迭代。

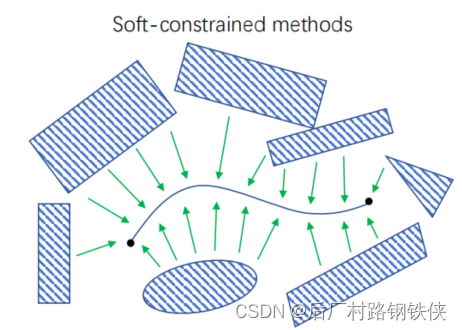
三、软约束

用一种虚拟的力将轨迹“推”至安全区域。