实验3二阶系统单位阶跃响应分析

一、实验目的：

 1、通过学习本实验内容，能够使用 MATLAB编程绘制 控制系统的单位阶跃响应曲线；

2、掌握二阶控制系统的阻尼比和自然振荡角频率对单位阶跃响应的影响。

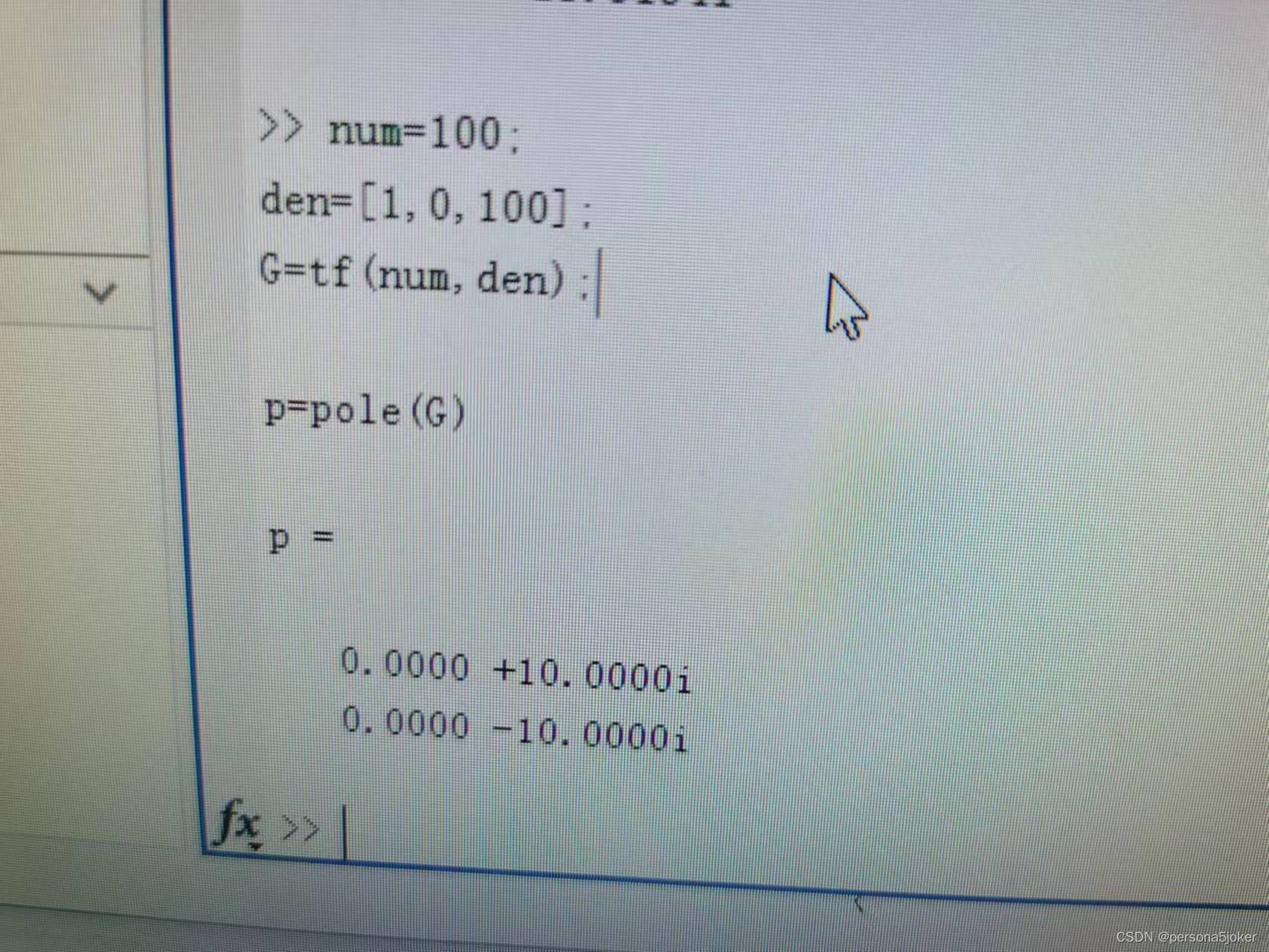
二、实验步骤：

1、闭环系统特征根／闭环极点：

典型二阶系统的闭环传递函数为：G（s）＝ω^2/(s^2+25£ωs+ω^2)

令ω＝10，£分别等于0，0.25，0.7，1，1.2时，求系统闭环极点，填入表3.1中，比较闭环极点于阻尼比£之间的关系，写出结论。

实验代码

1.num=100;

den=[1,0,100];

G=tf(num,den);

p=pole(G)

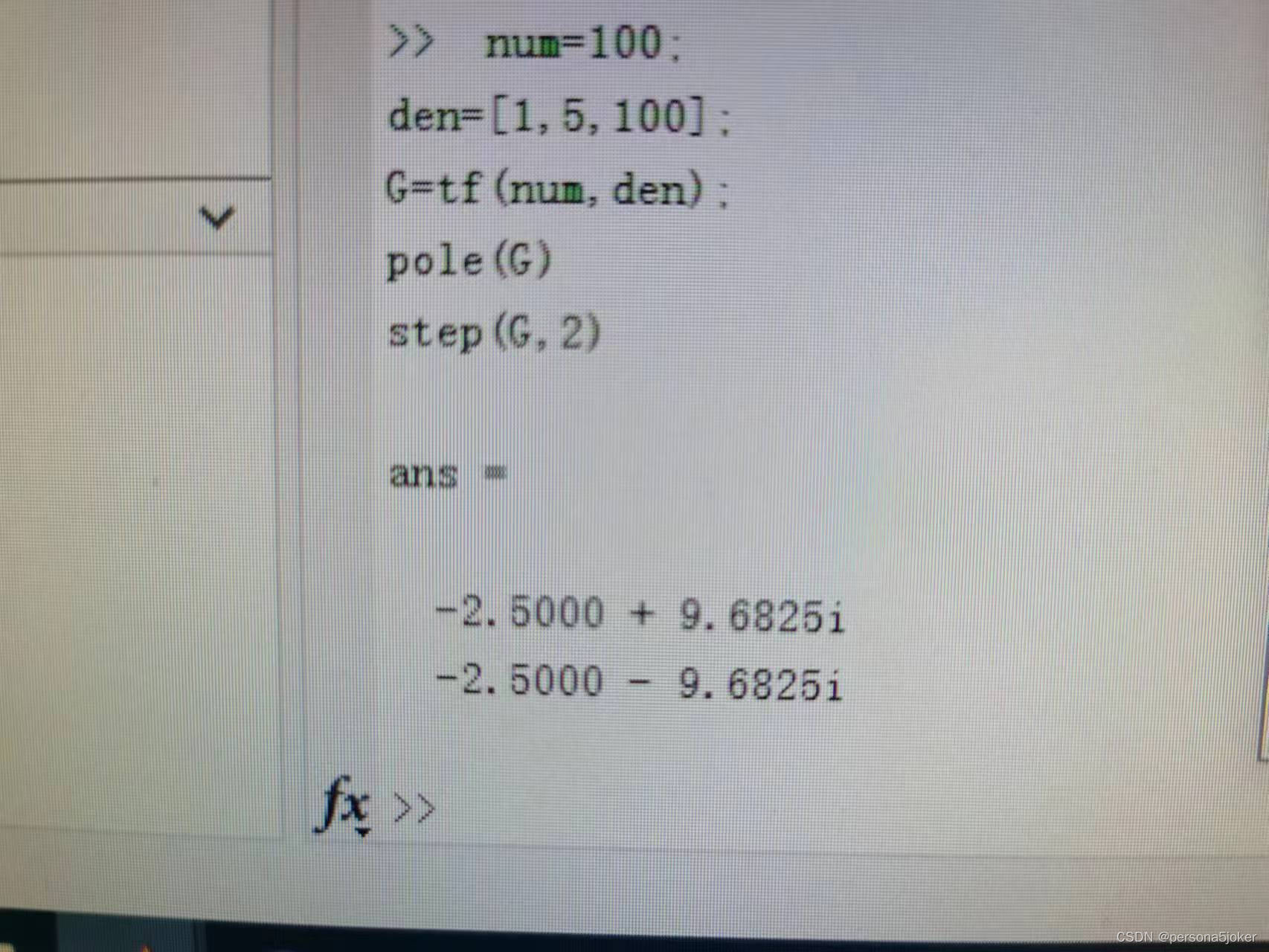
实验代码

2.num=100;

den=[1,5,100];

G=tf(num,den);

p=pole(G)

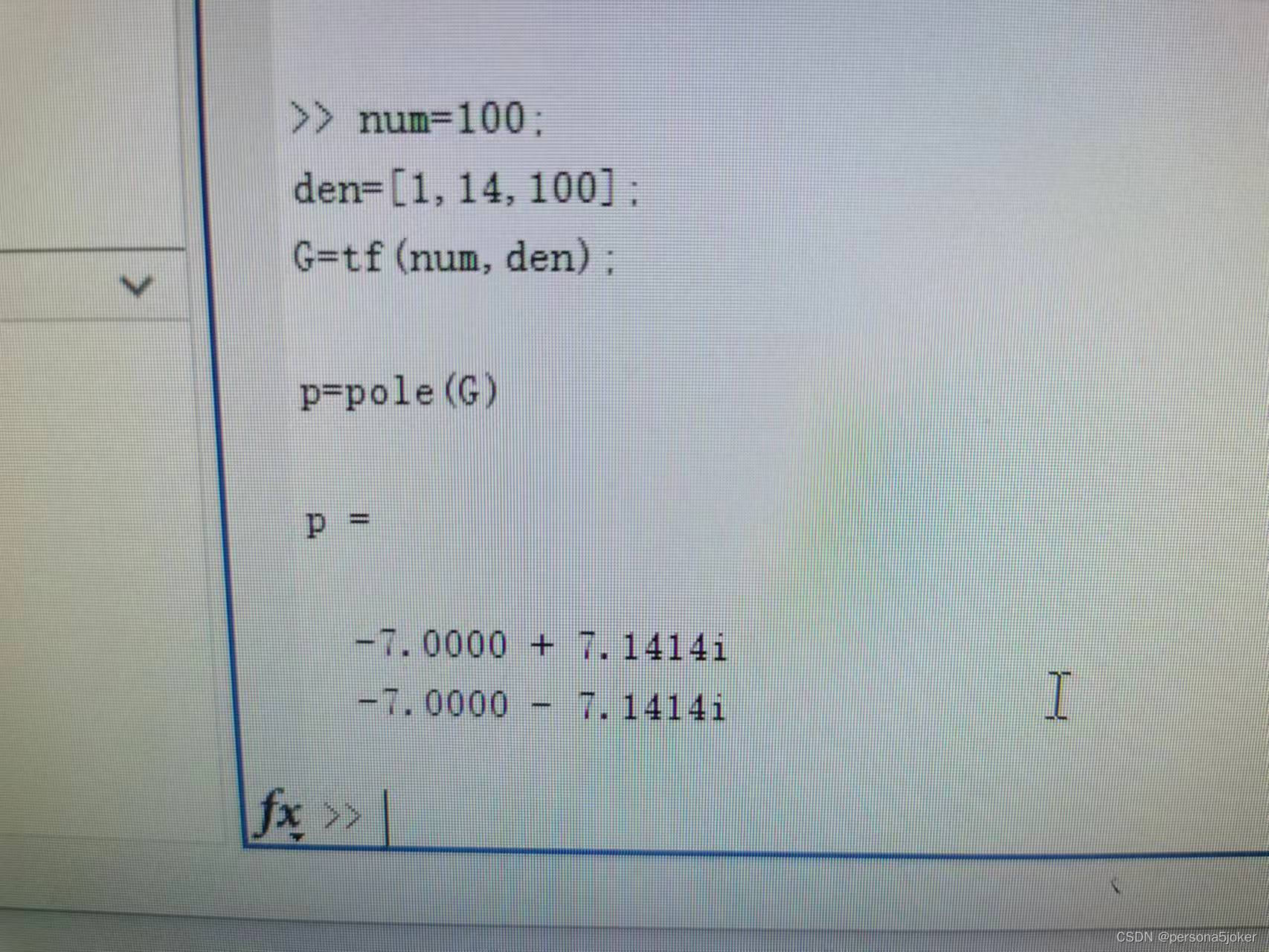
实验代码

3.num=100;

den=[1,14,100];

G=tf(num,den);

p=pole(G)

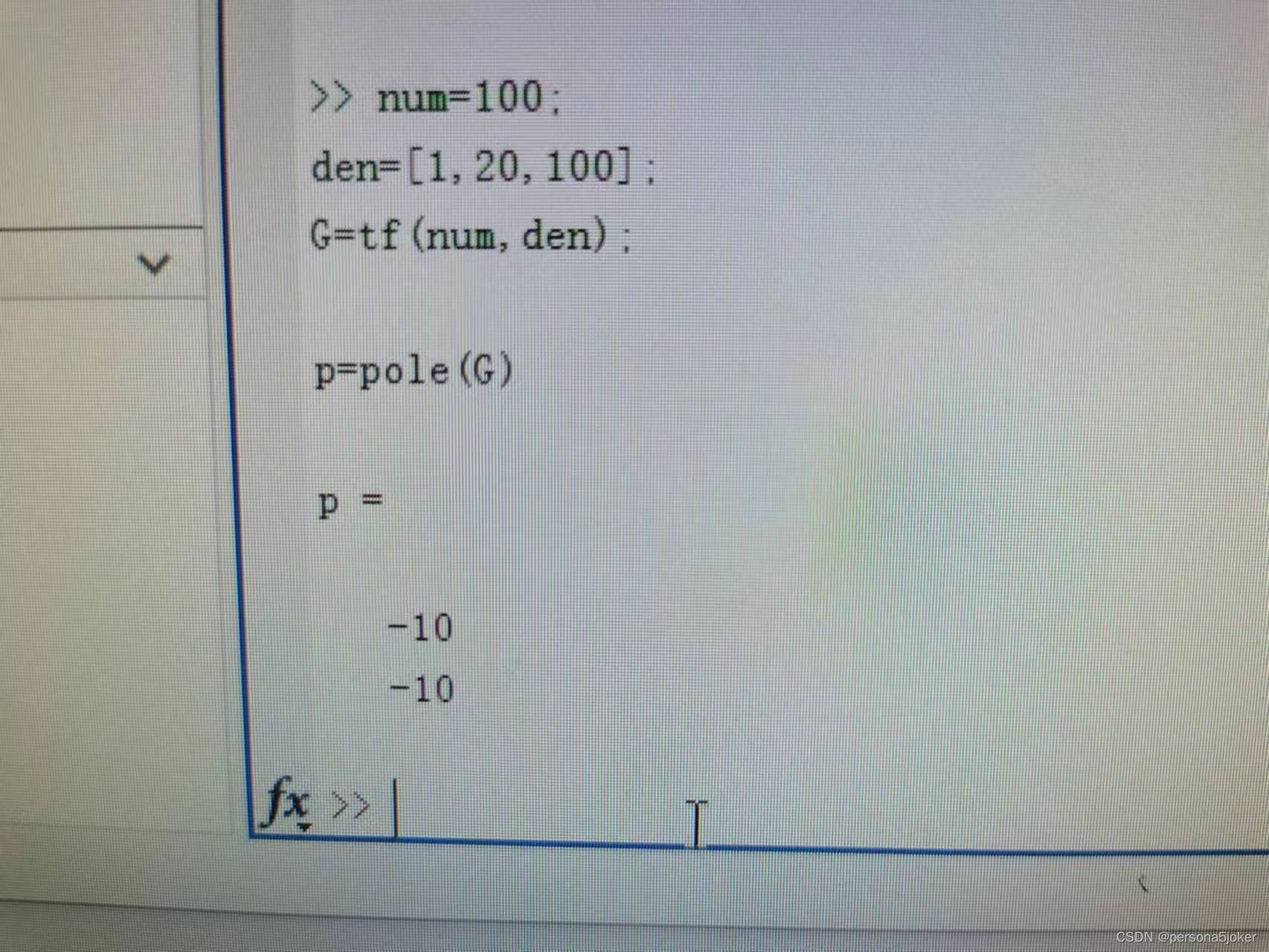
实验代码

4.num=100;

den=[1,20,100];

G=tf(num,den);

p=pole(G)

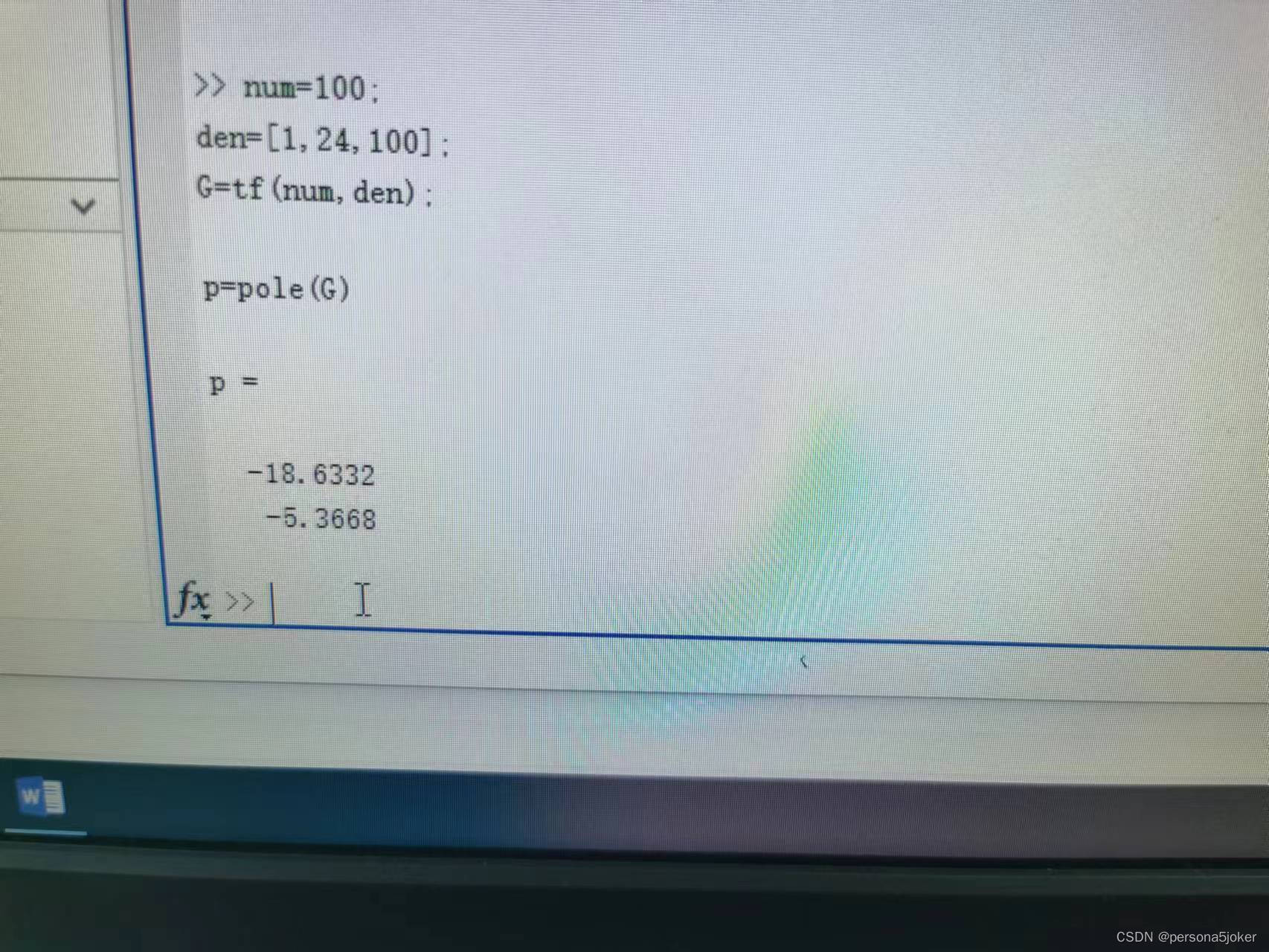
实验代码

5.num=100;

den=[1,24,100];

G=tf(num,den);

p=pole(G)

表3.1：二阶系统闭环极点（▲=2%）

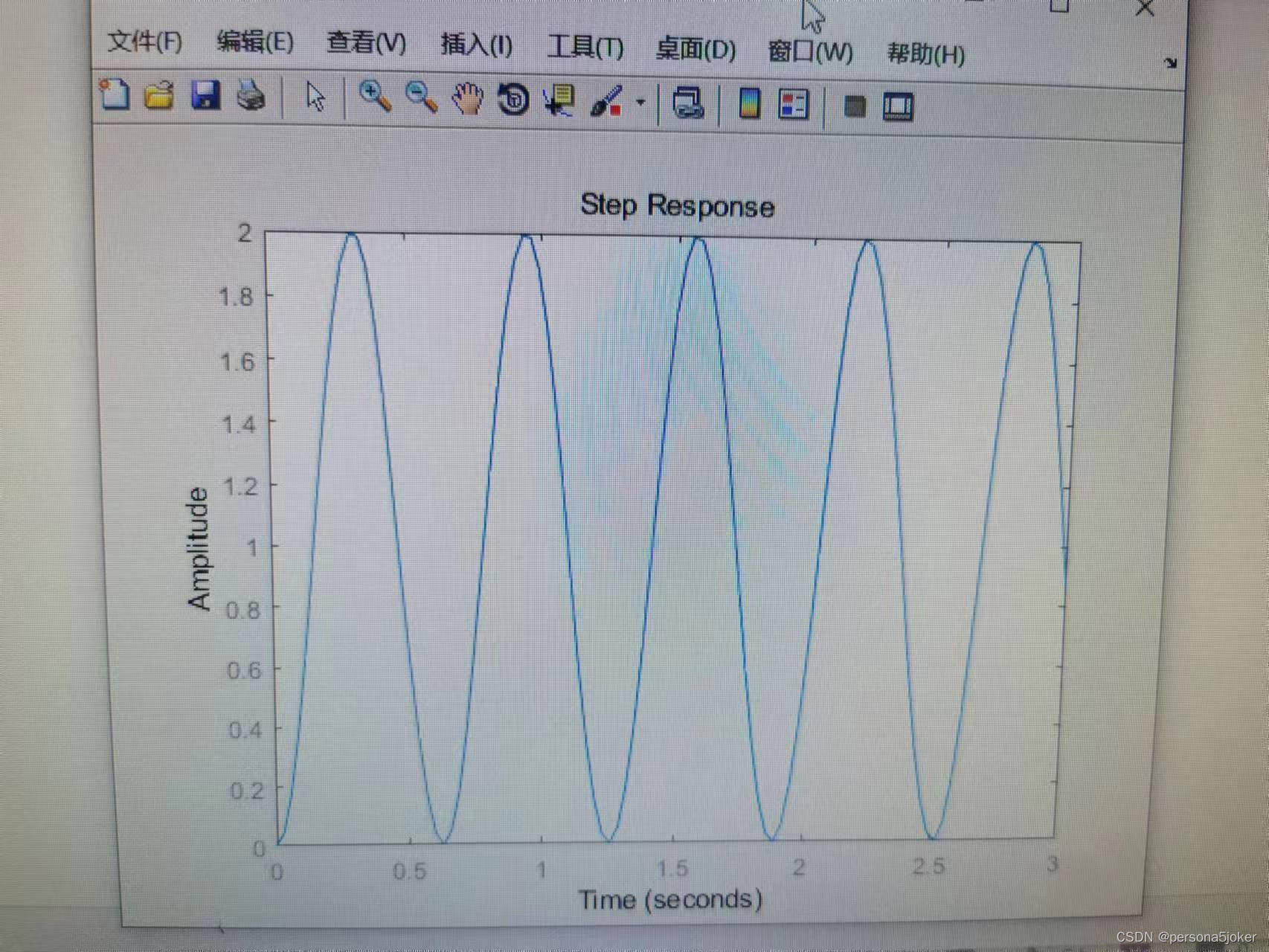
2、二阶系统单位阶跃响应分析：

(1)观察阻尼比£ 对二阶系统阶跃响应的影响

令ω＝10，£分别等于0，0.25，0.7，1，1.2时，绘制二阶系统单位阶跃响应曲线，分别读取动态性能指标，填入表3.2，同时需附上有标注数据的阶跃响应曲线图，根据实验结果，分析闭环极点、阻尼比与动态性能之间的关系，写出实验结论。

（图片鼠标右键点击查看参数）

1.实验代码：

num=100;

den=[1,0,100];

G=tf(num,den);

step(G,2)

结果：等幅振荡

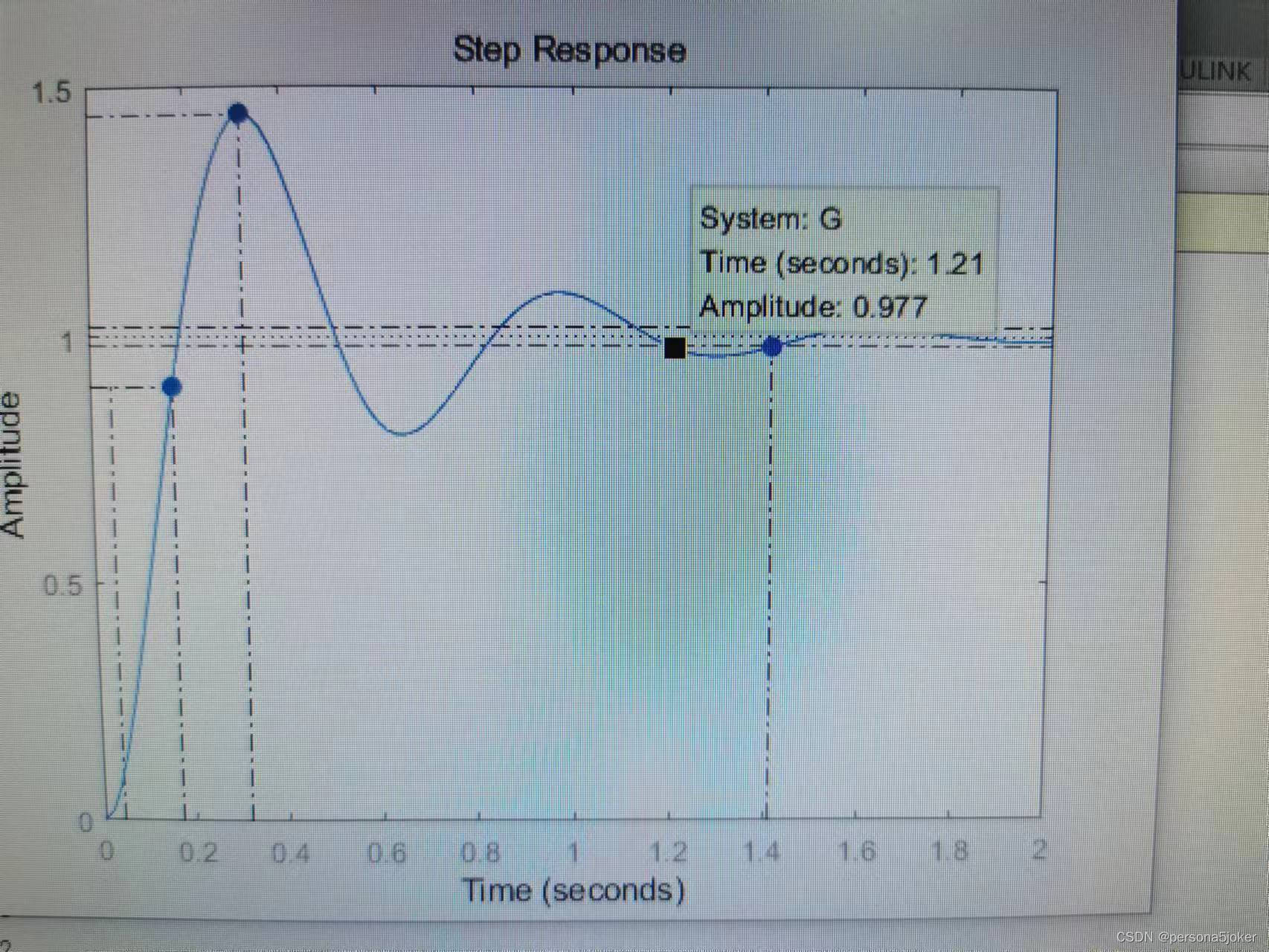
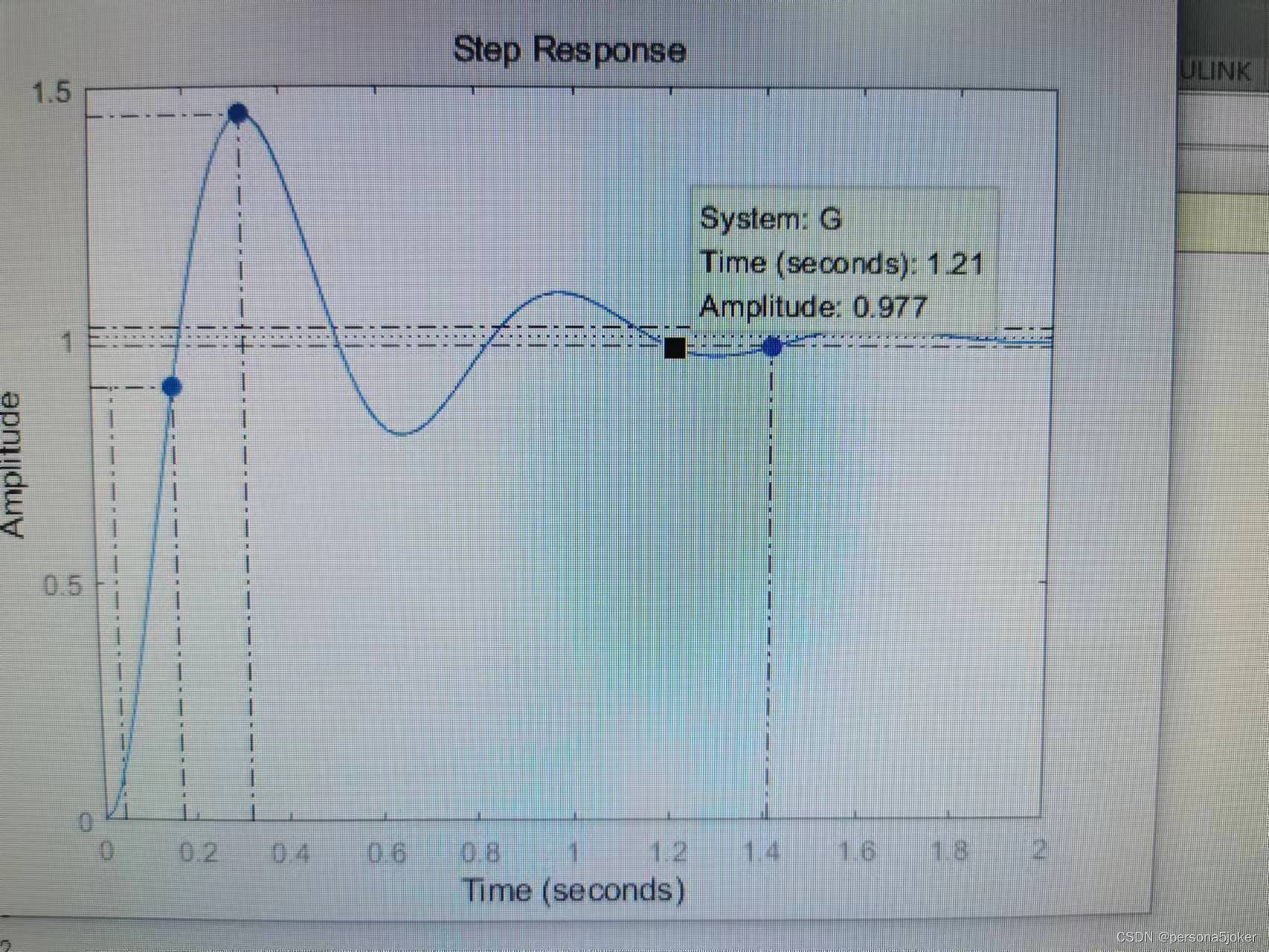
2实验代码：

.num=100;

den=[1,5,100];

G=tf(num,den);

step(G,2)

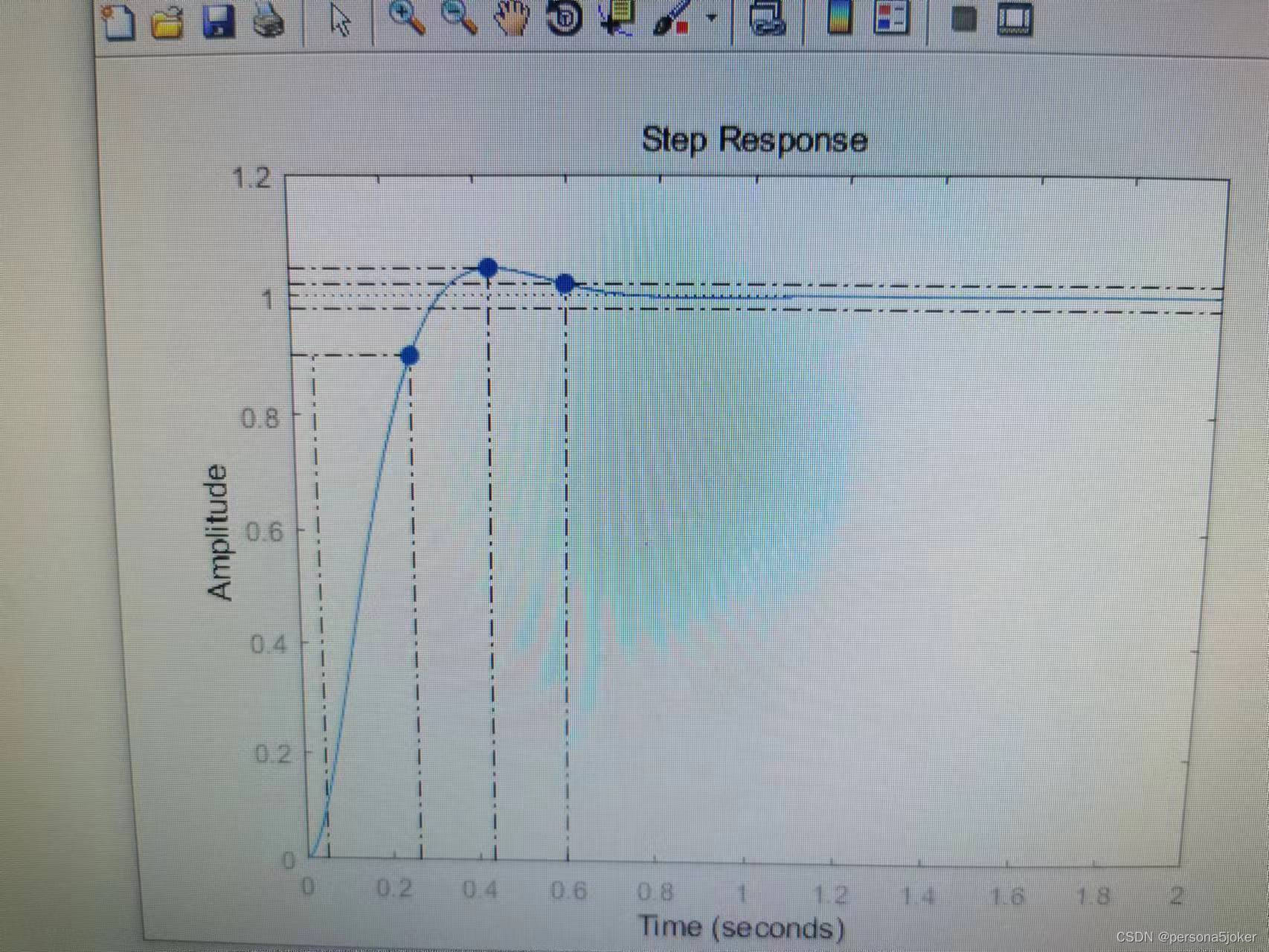
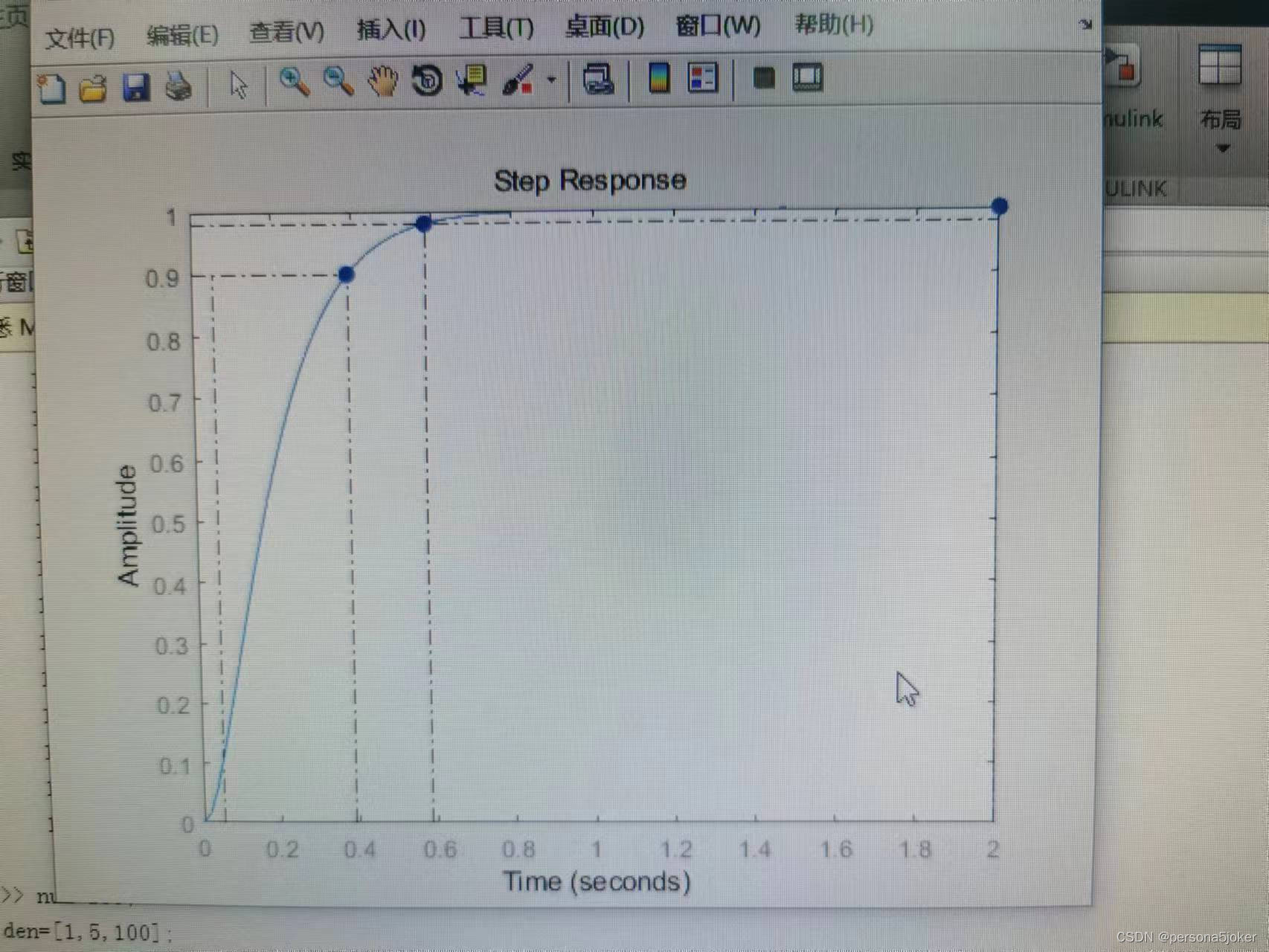
3实验代码：

num=100;

den=[1,14,100];

G=tf(num,den);

step(G,2)

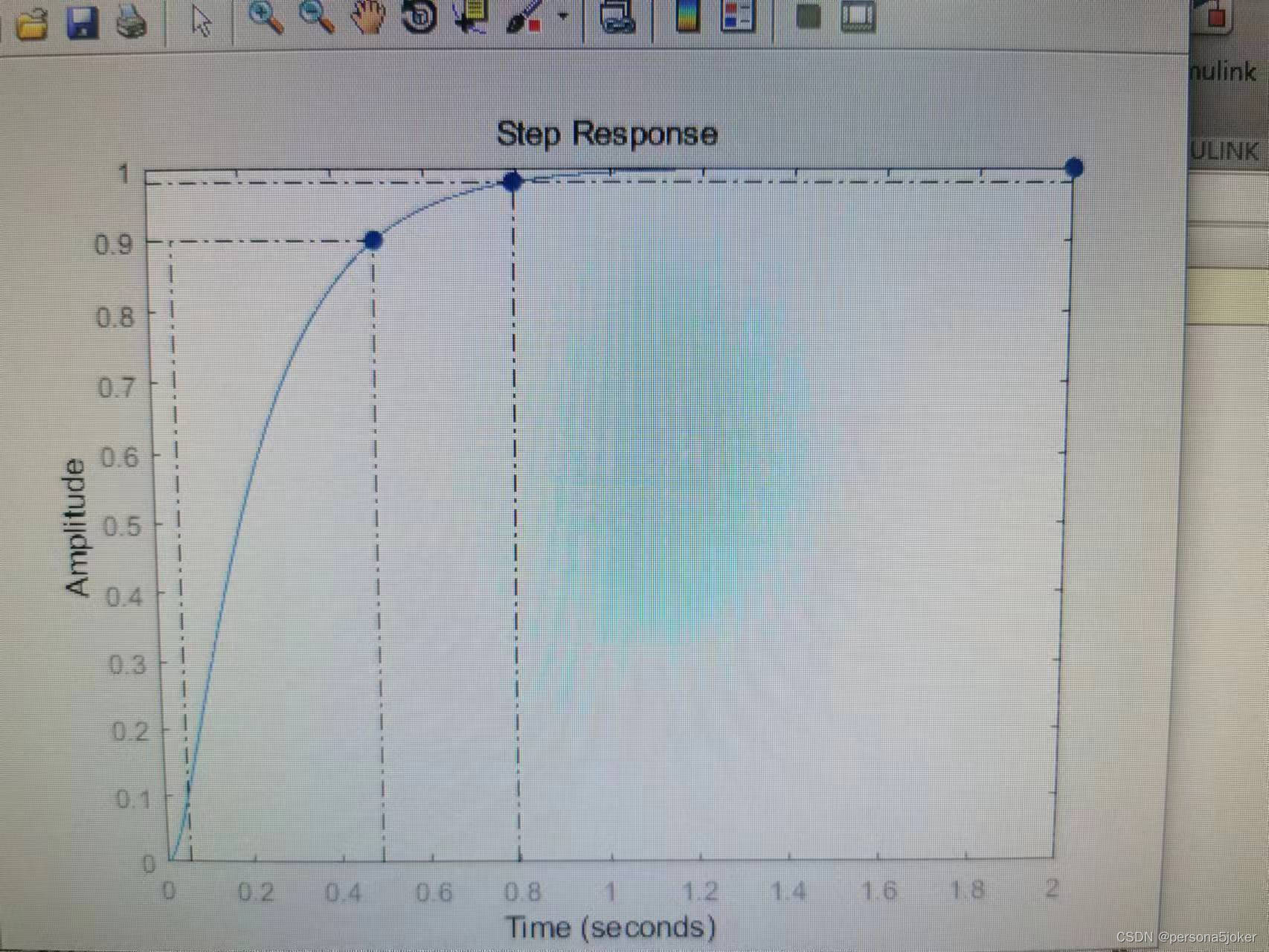
4实验代码

num=100;

den=[1,20,100];

G=tf(num,den);

step(G,2)

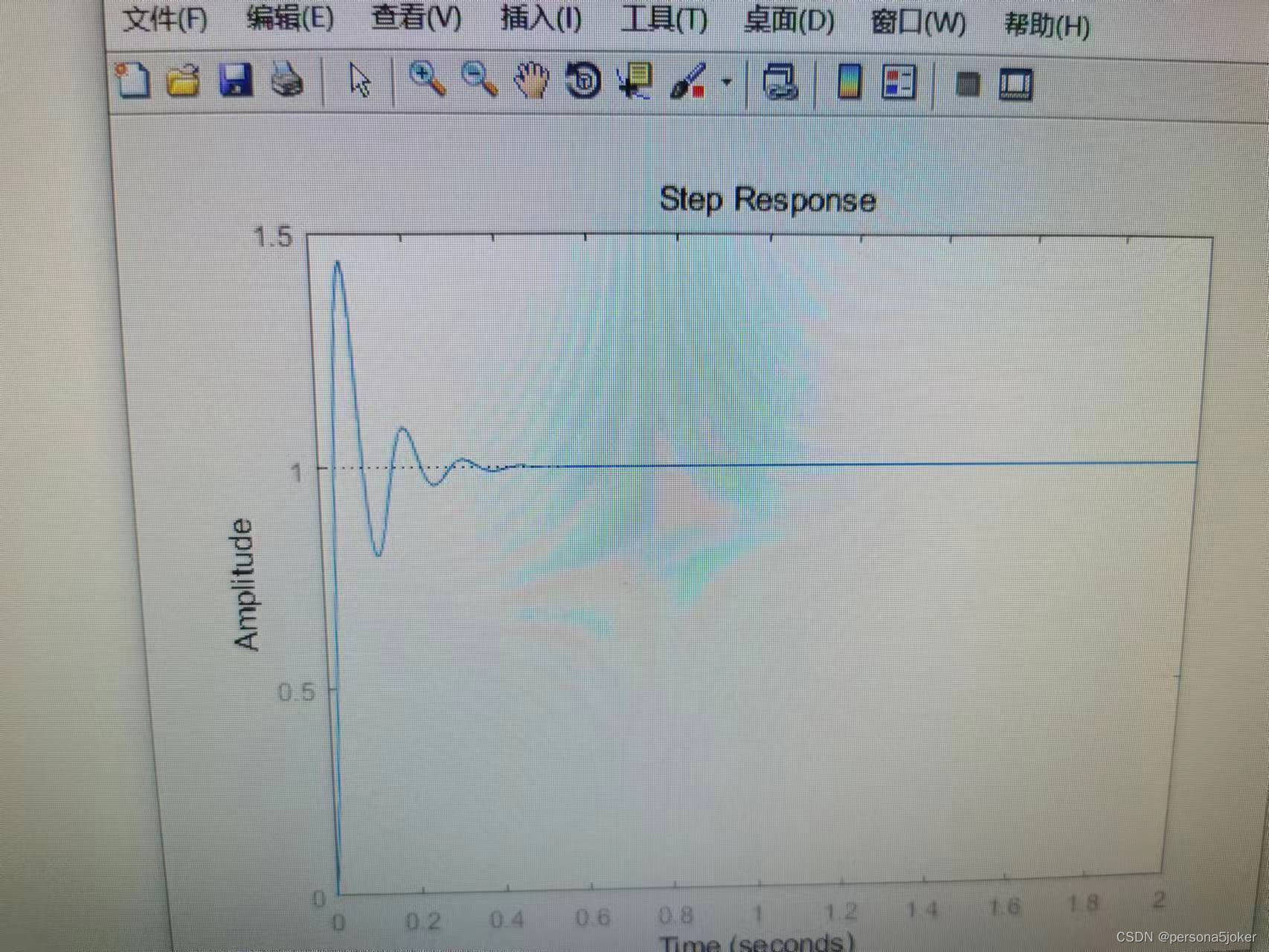
5.实验代码

num=100;

den=[1,24,100];

G=tf(num,den);

step(G,2)

表3.2：二阶系统动态性能分析比较（ω＝10，▲=2%）

结论：增大阻尼比，可以减少超调量，减小甚至消除振荡，但是会使系统响应变慢。

(2)观察振荡频率ω对二阶系统阶跃响应的影响：

令£=0.25，ω分别等于10，50时，闭环极点，并绘制二阶系统单位阶跃响应曲线，分别读取动态性能指标，填入表3.3，同时需附上有标注数据的阶跃响应曲线图，根据实验结果分析闭环极点、阻尼比与动态性能之间的关系，写出实验结论。

1实验代码：

num=100;

den=[1,5,100];

G=tf(num,den);

step(G,1)

2实验代码

num=2500;

den=[1,25,2500];

G=tf(num,den);

step(G,1)

表3.3：二阶系统动态性能分析比较（£=0.25，▲=2%）

结论：在阻尼比不变的情况下，增大振荡频率，可以减小上升时间，调节时间，峰值时间，使系统响应变快。