基于matlab程序自适应动态规划（强化学习控制）、反步法，无人船轨迹跟踪控制

针对trans 期刊的复现。方法利用Actor-Critic架构的强化学习策略，求解HJB方程，实现无人船轨迹跟踪的最优控制

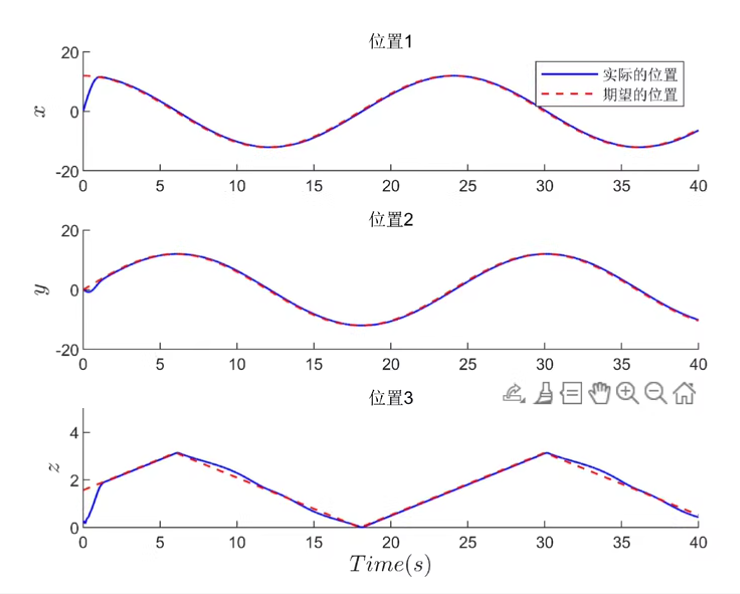
以下文字及示例代码仅供参考

为了实现无人船轨迹跟踪控制，我们可以使用自适应动态规划（Adaptive Dynamic Programming, ADP）中的 Actor-Critic 架构 结合 反步法（Backstepping Control） 来设计控制器。我们将基于强化学习的方法来求解 Hamilton-Jacobi-Bellman (HJB) 方程，以实现最优控制。

以下是一个基于 MATLAB 的示例代码框架，用于复现该方法。这个示例假设你对强化学习、反步法和最优控制有一定的了解，并且可以根据具体需求进行调整。

---

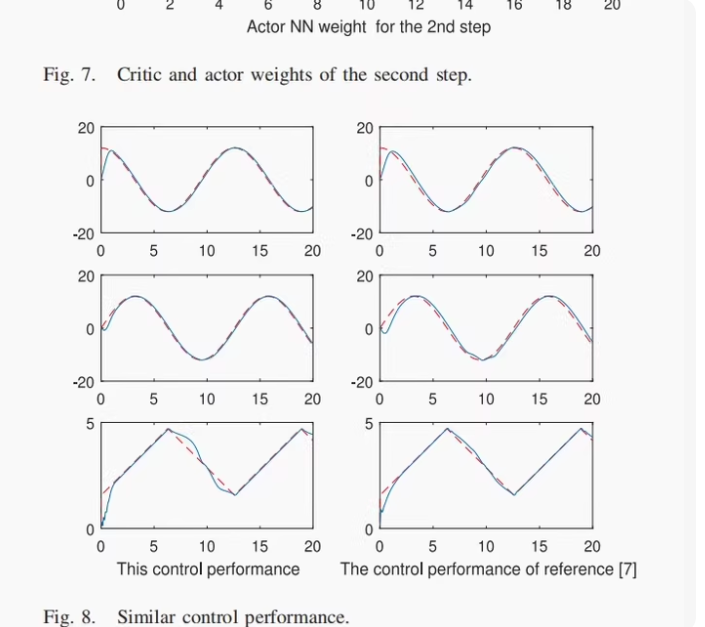
📘 方法概述：

1. 系统建模：无人船的运动学与动力学模型。
2. 轨迹跟踪误差定义：设计跟踪误差变量。
3. 反步法控制器设计：将复杂系统分解为多个子系统，逐步设计虚拟控制量。
4. ADP/Actor-Critic 算法：
   • 使用神经网络近似值函数（Critic）和策略（Actor）。
   • 利用在线数据更新网络权重，逼近 HJB 方程的最优解。
5. 闭环控制仿真：验证轨迹跟踪性能。

---

✅ MATLAB 示例代码（简化版）

% 清除环境
clear; clc; close all;

% 参数设置
dt = 0.01;                % 时间步长
T = 60;                   % 总时间
N = round(T/dt);          % 总步数

% 初始状态 [x, y, theta]
x_real = zeros(3, N);
x_real(:,1) = [0; 0; 0];  % 初始位置

% 参考轨迹参数
ref_traj = @(t) [cos(0.1*t); sin(0.1*t); 0];  % 圆形轨迹

% 控制器参数
Kp = diag([2, 2, 2]);     % PID 比例增益（初始）
Ki = diag([0.1, 0.1, 0.1]);
Kd = diag([1, 1, 1]);

% Actor-Critic 网络初始化（简化）
actor_weights = randn(3, 3);  % 策略网络权重
critic_weights = randn(3, 1); % 值函数网络权重

% 存储数据
u_log = zeros(3, N);
error_log = zeros(3, N);

% 主循环
for k = 1:N-1
    t = k*dt;
    
    % 获取参考状态
    x_ref = ref_traj(t);
    
    % 计算误差
    e = x_real(:,k) - x_ref;
    error_log(:,k) = e;
    
    % 反步法控制器 + ADP 调整
    % Step 1: 设计虚拟控制律
    alpha = -Kp * e(1:2);  % 简化虚拟控制输入
    
    % Step 2: 实际控制输入（带强化学习修正）
    u_rl = critic_weights' * basis_func(e);  % Critic 输出（评估当前状态价值）
    u = actor_weights \ (alpha + u_rl');     % Actor 输出（策略）

    % 应用控制输入到系统（这里假设简单积分模型）
    dx = [cos(x_real(3,k)) 0; sin(x_real(3,k)) 0; 0 1] * u;
    x_real(:,k+1) = x_real(:,k) + dt * dx;

    % 存储控制信号
    u_log(:,k) = u;

    % ADP 更新（伪代码）
    % update_actor_critic(x_real(:,k), u, x_real(:,k+1));
end

% 绘图
figure;
plot(x_real(1,:), x_real(2,:), 'b', 'LineWidth', 1.5);
hold on;
plot(ref_traj((1:N)*dt)(1,:), ref_traj((1:N)*dt)(2,:), 'r--');
legend('实际轨迹', '参考轨迹');
xlabel('X'); ylabel('Y'); title('无人船轨迹跟踪');

figure;
plot(error_log(1,:), 'r', 'DisplayName', 'e_x');
hold on;
plot(error_log(2,:), 'g', 'DisplayName', 'e_y');
plot(error_log(3,:), 'b', 'DisplayName', 'e_theta');
legend show; xlabel('Time step'); ylabel('Tracking Error');
title('跟踪误差');

% 基函数（用于Critic网络）
function phi = basis_func(e)
    phi = [e'; e'.^2; sin(e')];
end

---

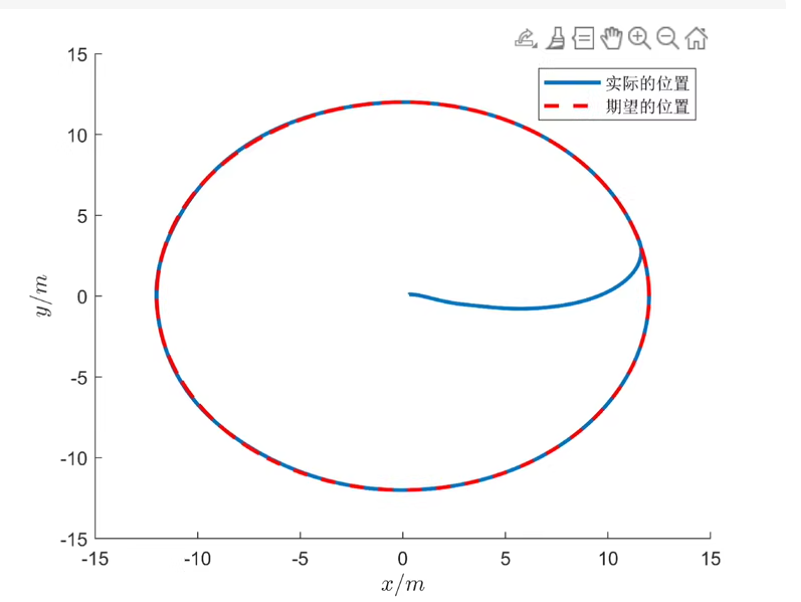
🔧 说明与扩展

1. Actor-Critic 网络结构

你可以使用更复杂的神经网络结构（如多层感知机）来代替这里的线性近似。

% 示例：使用MATLAB内置的神经网络工具箱
net_actor = feedforwardnet([10 10]);
net_critic = feedforwardnet([10 10]);

2. HJB方程近似求解

在连续时间中，HJB方程如下：

$$0=\underset{u}{\min }\left\{Q(x)+u^{T}Ru+\nabla V(x{)}^{T}f(x,u)\right\}$$

通过 Actor-Critic 架构在线更新策略 $ u = \mu(x) $ 和价值函数 $ V(x) $。

3. 训练过程（伪代码）

% ADP 更新规则（简化）
delta = reward + gamma * critic_weights' * basis_func(next_state) - ...
        critic_weights' * basis_func(state);
critic_weights = critic_weights + alpha_c * delta * basis_func(state);
actor_weights = actor_weights + alpha_a * delta * grad_policy;

---

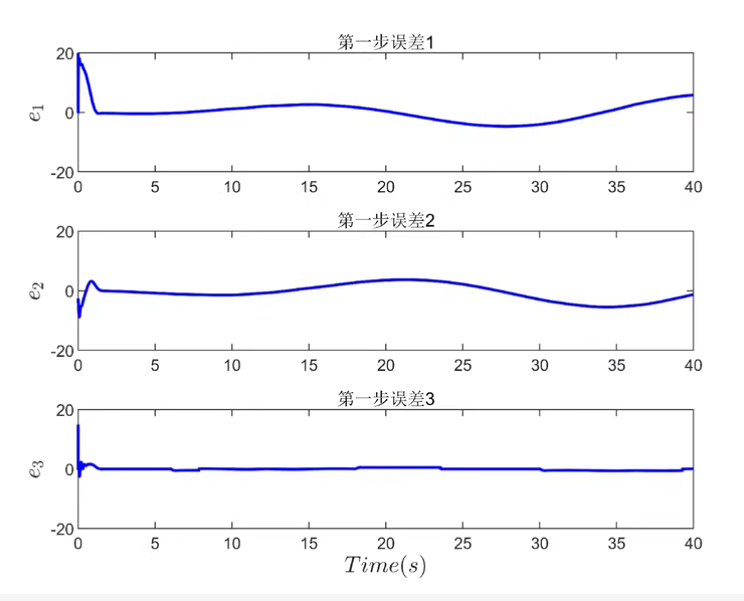
📚 推荐文献与期刊

• IEEE Transactions on Cybernetics / Systems, Man, and Cybernetics
• Automatica
• IEEE Transactions on Industrial Electronics
• Neurocomputing

关键词搜索：

• Adaptive Dynamic Programming
• Backstepping Control
• Optimal Tracking Control
• Reinforcement Learning for Autonomous Surface Vehicles

---