一、引言

一元线性回归：涉及的变量只有一个

多元线性回归：涉及的变量两个或两个以上

预测结果与真实值是有一定的误差（如图）：

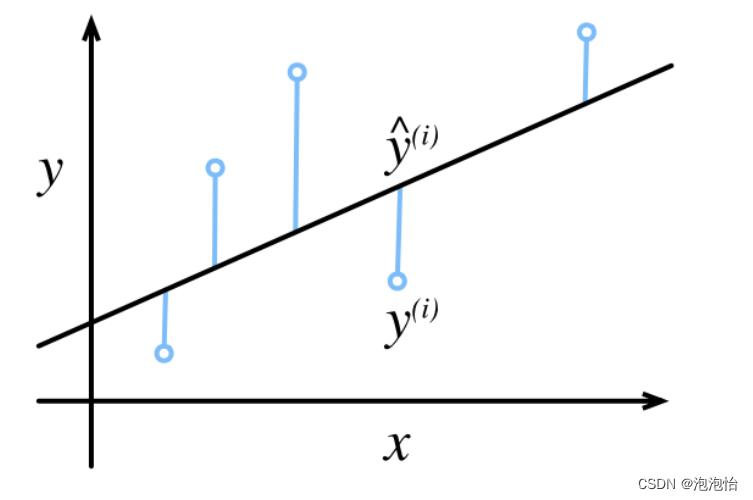
 本文以y=-2x+8的数据进行拟合为例，给出了利用最小二乘法来估计回归系数的方法及python实现。

二、公式推导

1.最小二乘法：

假设已知一系列的散点（xi,yi)

我们将（xi,yi)代入 y =kx+b 得

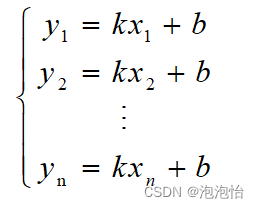
 构造最小二乘函数：

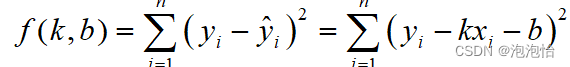
 对k和b分别求偏导数得：

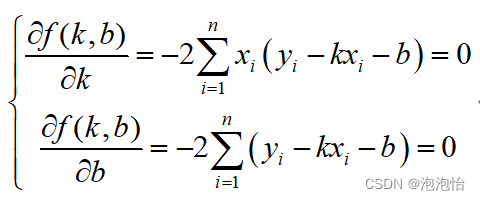
上述方程组两端同时除以n得：

 

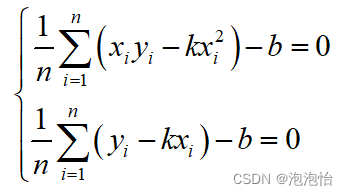
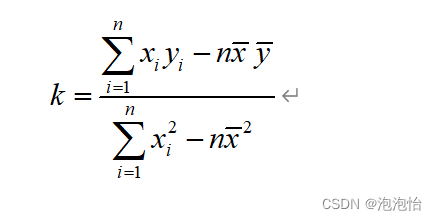
 将其代入即可得到系数b。

 三、python程序

1.根据散点图判读曲线变化趋势

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trainX=np.arange(25)
trainY=2*trainX+8+np.random.randn(25)
plt.scatter(trainX, trainY,color='red',marker='+')

结果如图所示：

 

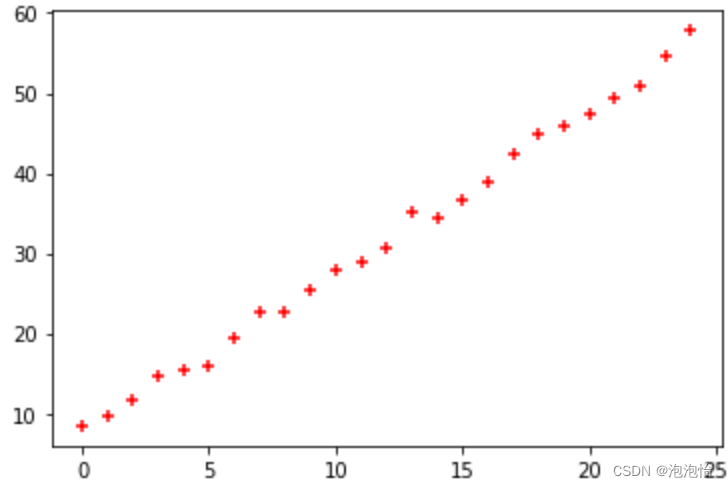
2.回归系数计算如下：

n=25
xu=np.sum(trainX)/n
yu=np.sum(trainY)/n
k1 = sum( trainX * trainY ) - n * xu * yu;
k2 = sum( trainX * trainX ) - n * xu * xu;
k = k1 / k2;
b = yu - k * xu;

 结果如下：k=2.0174825107892924, b=7.508028732222016

3.完整代码如下

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trainX=np.arange(25)
trainY=2*trainX+8+np.random.randn(25)
plt.scatter(trainX, trainY,color='red',marker='+')
n=25
xu=np.sum(trainX)/n
yu=np.sum(trainY)/n
k1 = sum( trainX * trainY ) - n * xu * yu;
k2 = sum( trainX * trainX ) - n * xu * xu;
k = k1 / k2;
b = yu - k * xu;
Y1=k*trainX+b
fig,ax = plt.subplots()
ax.scatter(trainX, trainY,color='red',marker='+')
ax.plot(trainX, Y1,color='blue')

 结果如图：

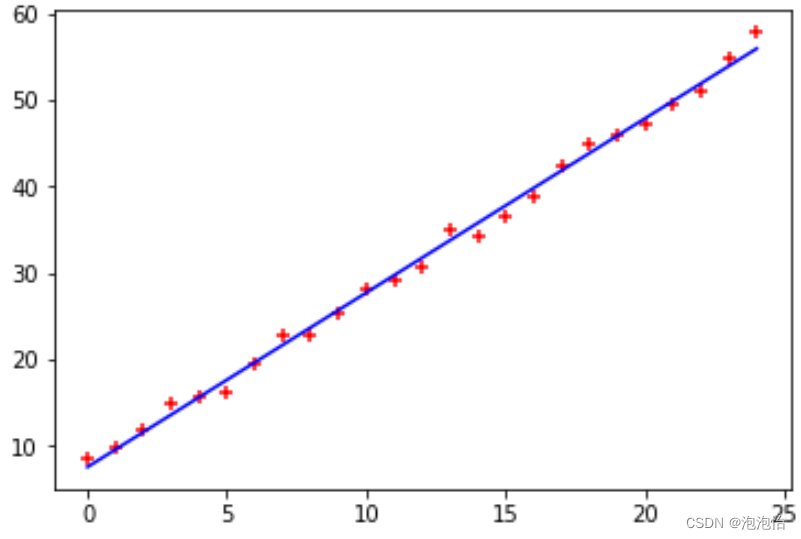
注意：附加最大似然估计的推导：