双方博弈复制动态方程(y-x,x=0.3,x=0.5,x=0.7)与matlab数值仿真——matlab2016a版本
双方博弈复制动态方程(y-x,x=0.3,x=0.5,x=0.7)与matlab数值仿真注明:源于对《基于演化博弈的装配式建筑应用研究》-金倩-4.4.1.1的政府与开发商的复制动态方程的matlab仿真1.输入常微分方程组%政府与开发商复制动态方程%F(x)=x(1-x)(70y-45)%F(y)=y(1-y)(97.97x-42.26)function dxdt=differential(t,
·
双方博弈复制动态方程(y-x,x=0.3,x=0.5,x=0.7)与matlab数值仿真——matlab2016a版本
注明:源于对《基于演化博弈的装配式建筑应用研究》-金倩-4.4.1.1的政府与开发商的复制动态方程的matlab仿真
1.输入常微分方程组
%政府与开发商复制动态方程
%F(x)=x(1-x)(70y-45)
%F(y)=y(1-y)(97.97x-42.26)
function dxdt=differential5(t,x)
dxdt=[x(1)*(1-x(1))*(70*x(2)-45);x(2)*(1-x(2))*(97.97*x(1)-42.26)]; %F(x(1)函数表示F(x),F(x(2))函数表示F(y)
end
保存为differential5.m文件
2.主函数
%y与x的坐标图
for i=0:0.1:1 %循环步长为0.1,(条件要有x,y,其初始值均为0,如何添加)
for j=0:0.1:1 % %循环步长为0.1
[T,Y]=ode45('differential5',[0 1],[i j]); %常微分方程中常用ODE45()函数,其调用格式为[T,Y]=ode45('求解的函数名',[T自变量区间],初始值向量,...)
figure(1) %图1
grid on %显示坐标轴网格线
plot(Y(:,1),Y(:,2)) %(逗号前是行,逗号前是列,冒号表示从第一行到最后一行;(Y(:,1)表示第一列的所有元素,相当于dx/dt,Y(:,2))表示第二列的所有元素相当于dy/dt
xlabel('x'); %x轴名称
ylabel('y') %y轴名称
% legend('ODE45 解','解析解') 曲线名称
hold on
axis([0,1,0,1])
end
end
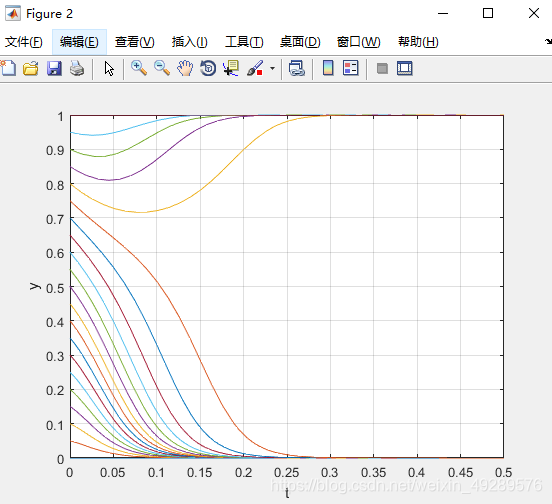
%dy/dt与t的坐标图,当x=0.3时
i=0.3
for j=0:0.05:1
[T,Y]=ode45('differential5',[0 0.5],[i j]);
figure(2) %图3
grid on
plot(T,Y(:,2))
xlabel('t'); %x轴名称
ylabel('y') %y轴名称
hold on
axis([0,0.5,0,1])
end
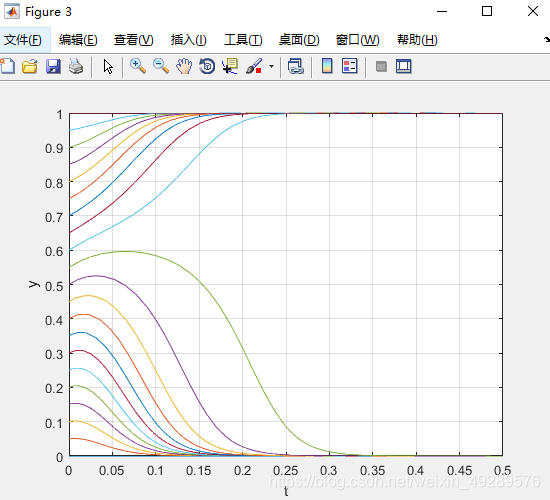
%dy/dt与t的坐标图,当x=0.5时
i=0.5
for j=0:0.05:1
[T,Y]=ode45('differential5',[0 0.5],[i j]);
figure(3) %图3
grid on
plot(T,Y(:,2))
xlabel('t'); %x轴名称
ylabel('y') %y轴名称
hold on
axis([0,0.5,0,1])
end
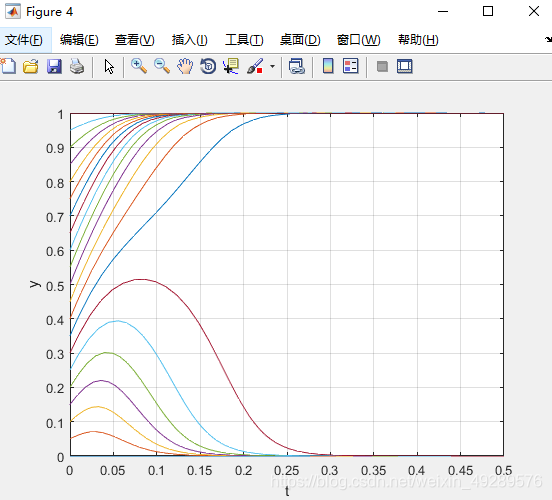
%dy/dt与t的坐标图,当x=0.7时
i=0.7
for j=0:0.05:1
[T,Y]=ode45('differential5',[0 0.5],[i j]);
figure(4) %图4
grid on
plot(T,Y(:,2))
xlabel('t'); %x轴名称
ylabel('y') %y轴名称
hold on
axis([0,0.5,0,1])
end
保存为for5.m文件
3.run结果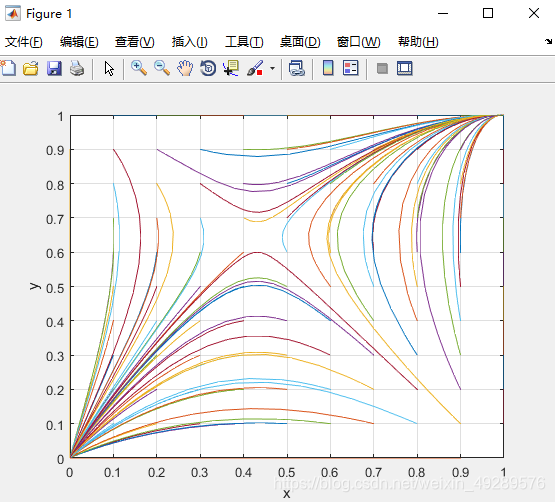

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容







所有评论(0)