联邦学习之纵向线性回归分析

1，背景介绍

A,B 双方利用纵向联邦算法共同训练线性回归模型，B 方拥有标签 y 为 active party，A为只有标签为 passive party。C为 Arbiter，一个中立的第三方。（Fate 的官方实现上并没有横向线性回归的例子）

Qestion 1：host 没有标签 y 如何参与训练更新模型？

需要预先知道的是，线性回归中我们的模型更新公式为：
$${\theta }_j:={\theta }_j-\frac{\alpha }{m}\sum _{i=1}^m\left(h_{\theta }\left(x^i\right)-(y^i\right))x_j$$
其实简而言之，θ=θ-g，g = dx。其中，θ为模型参数，g为梯度，d为残差。所以任何参与方只要获得了d，用自己的 x 便可以更新模型。这样就说明了 host 如何参与模型训练的。

具体的线性回归背景可参考：线性回归理论及实践

2，理论推导

定义：全局损失函数如（5），θ表示模型参数，λ表示惩罚系数；（6）式表示加密后用u表示的损失函数；然后我们将（6）展开，分别用$[[L_A]]$,$[[L_B]]$$[[L_{AB}]]$表示A方，B方的损失，以及含有AB双方的损失，得到（7）式；再然后我们将含有AB双方模型的那一项令为[[d]]，由此求得双方各自的梯度得到（8）（9）.

tips：线性回归模型中，我们通常使用梯度下降法不断迭代梯度值直到模型收敛找到最小损失。因此，对于训练来讲，双方都需要梯度数据。

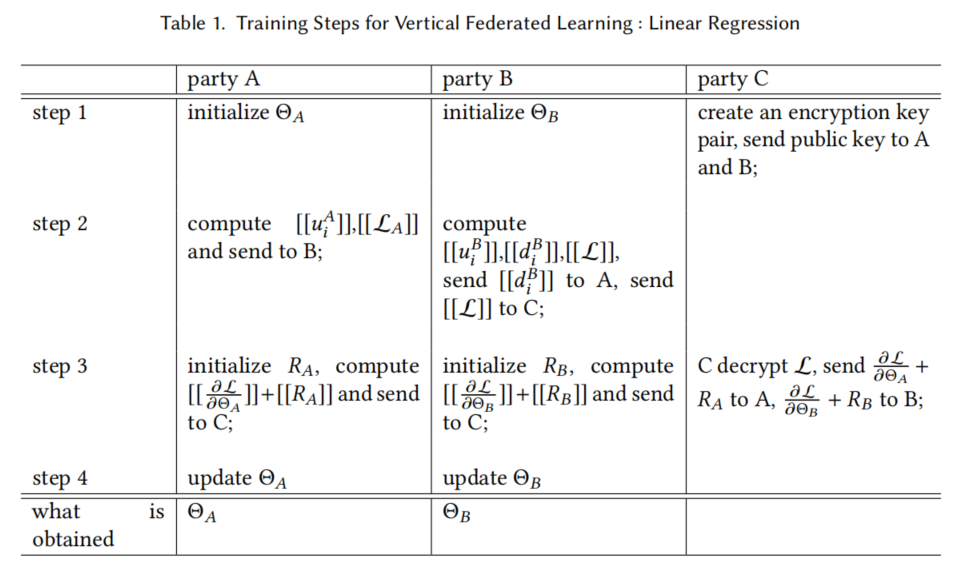
训练过程如下：

第一步：A,B初始化参数，C生成密钥对，并分发公钥；

第二步：A计算模型A和损失A并发给B；B收到后便可以计算损失并发送给C，d发送给A以及模型B；

第三步：A生成随机数RA，计算[[梯度A+RA]]发送给C；B生成随机数RB，计算[[梯度B+RB]]发送给C；C解密并返回；

第四步：AB分别减去各自的随机数便得到共同训练的全局梯度，然后各自更新模型。

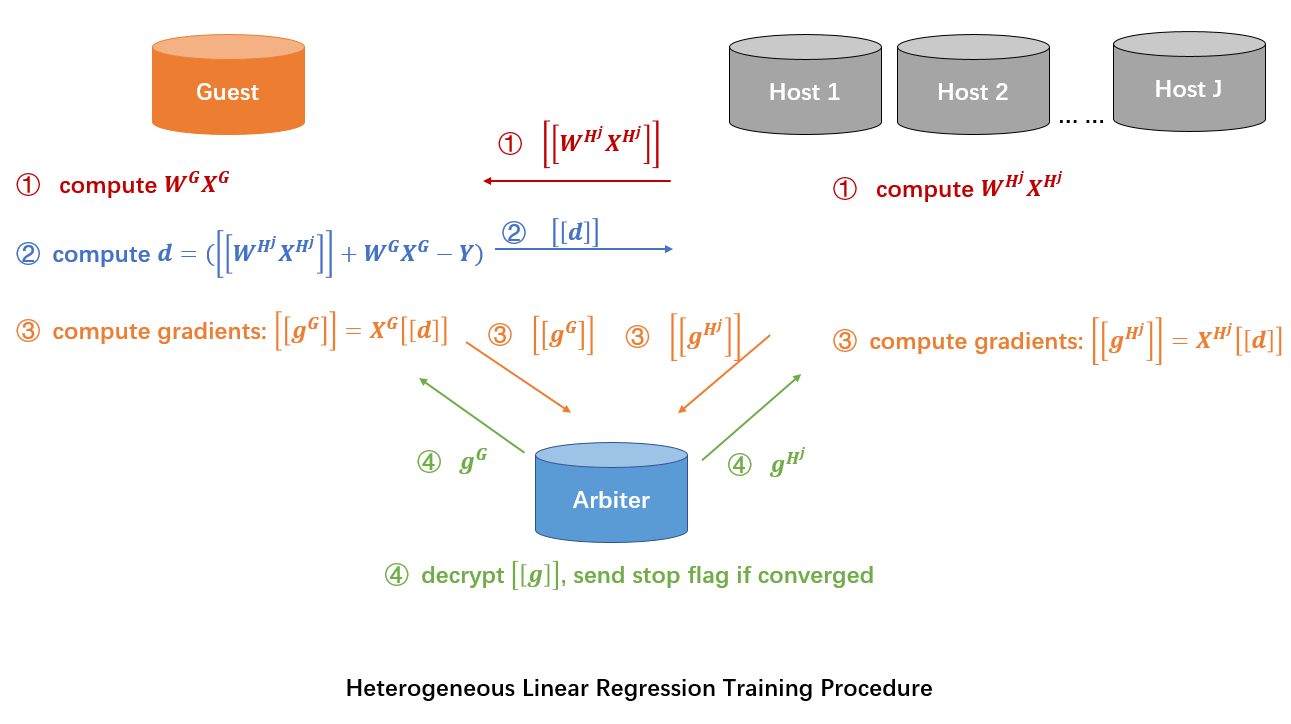
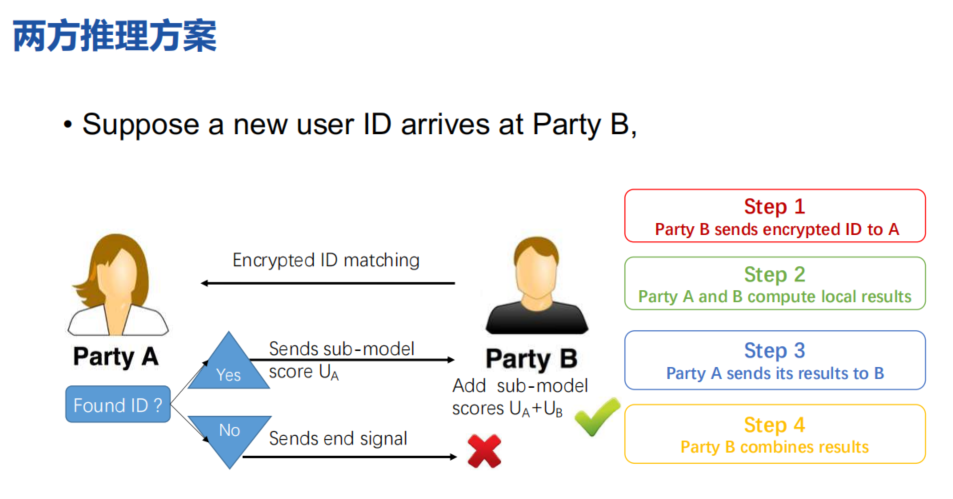
预测过程如下：

通过协调方C输入用户特征，AB分别计算结果并发送给C，C将结果相加即得到最终结果。

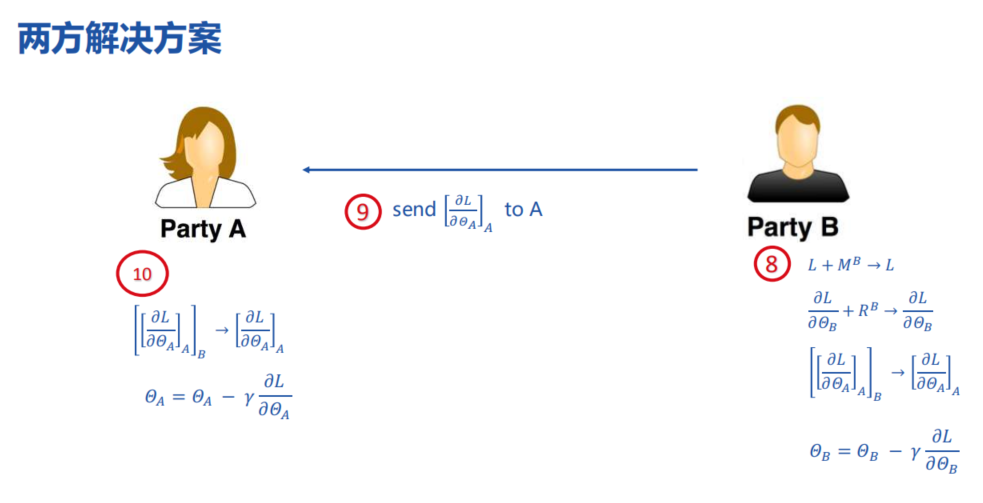
3，纵向线性回归的两方解决方案

思考：上面的协作者C仅仅是分发公钥以及判断收敛的作用。可以可不要呢？

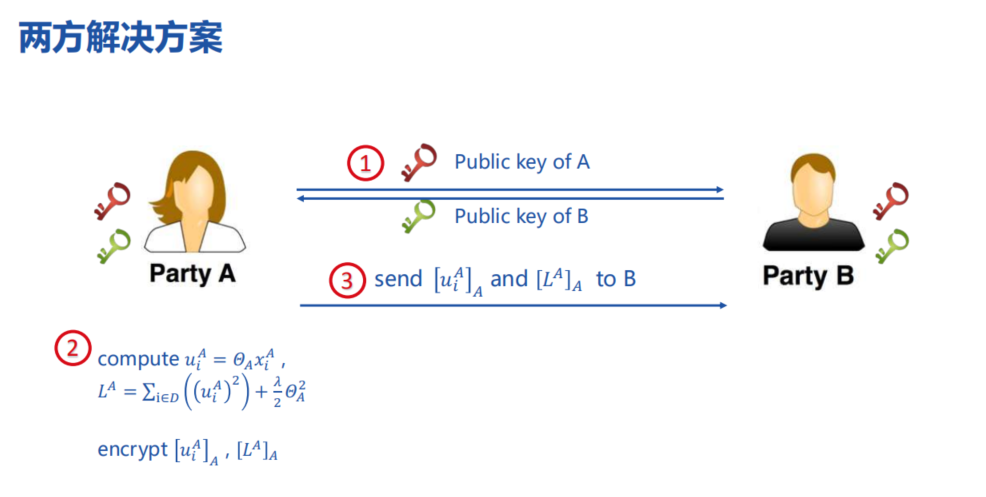
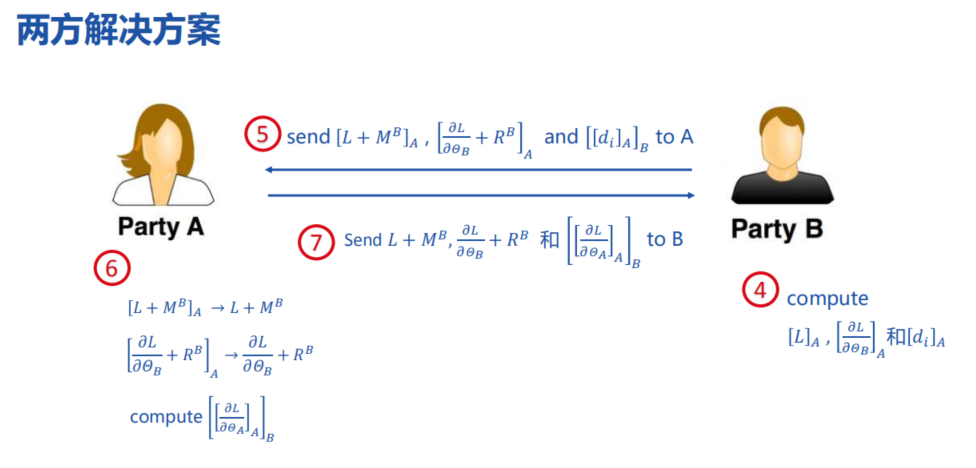
纵向线性回归的两方解决方案：