之前写了 matlab heaviside函数生成矩形脉冲，以及如何用傅里叶级数如何近似：表示矩形脉冲 matlab 模拟吉布斯效应。
现在我们滤除周期的矩形脉冲信号的高频部分，也就是做一个低通滤波器。

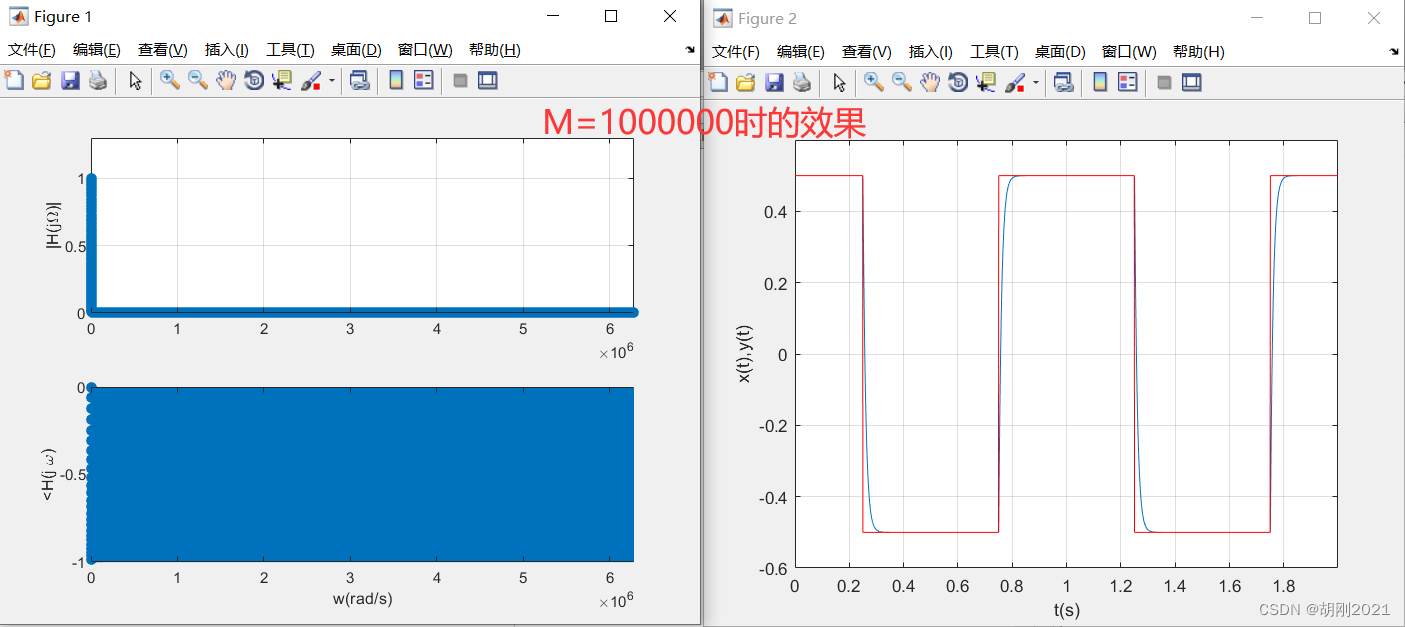
这一节我们处理的周期的矩形脉冲信号与前几节不同，它的均值为0，也就是前几节的信号沿着Y轴向下移动1个单位，这样它的傅里叶级数表示就没有了直流分量1，也就是没有了 $\Omega =0$ 的分量。

下面是题目表述

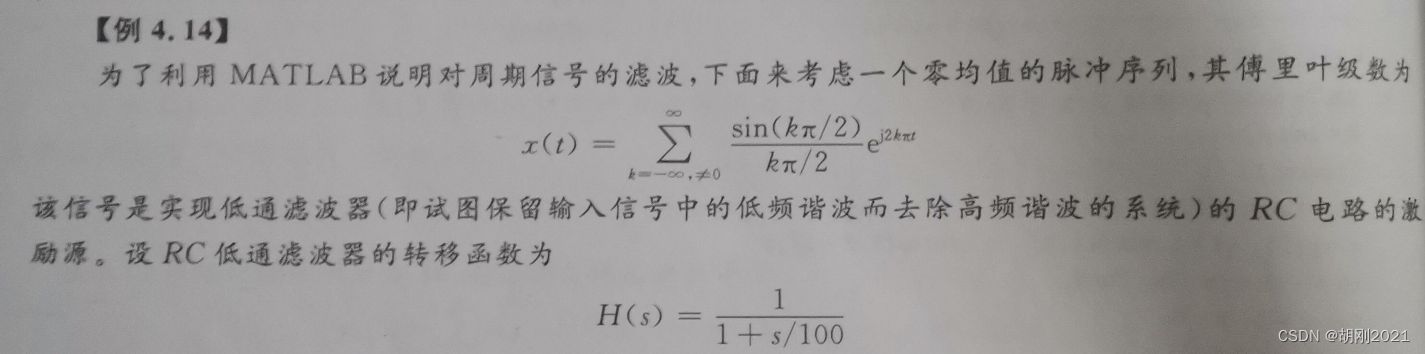
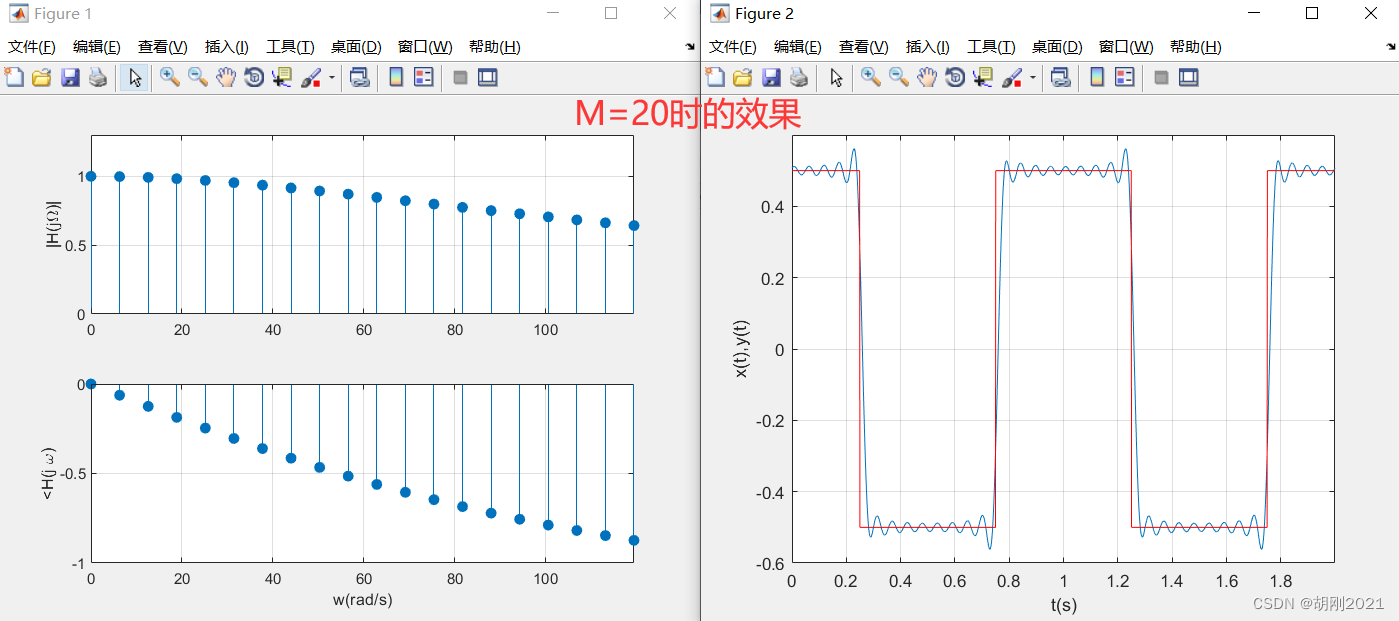
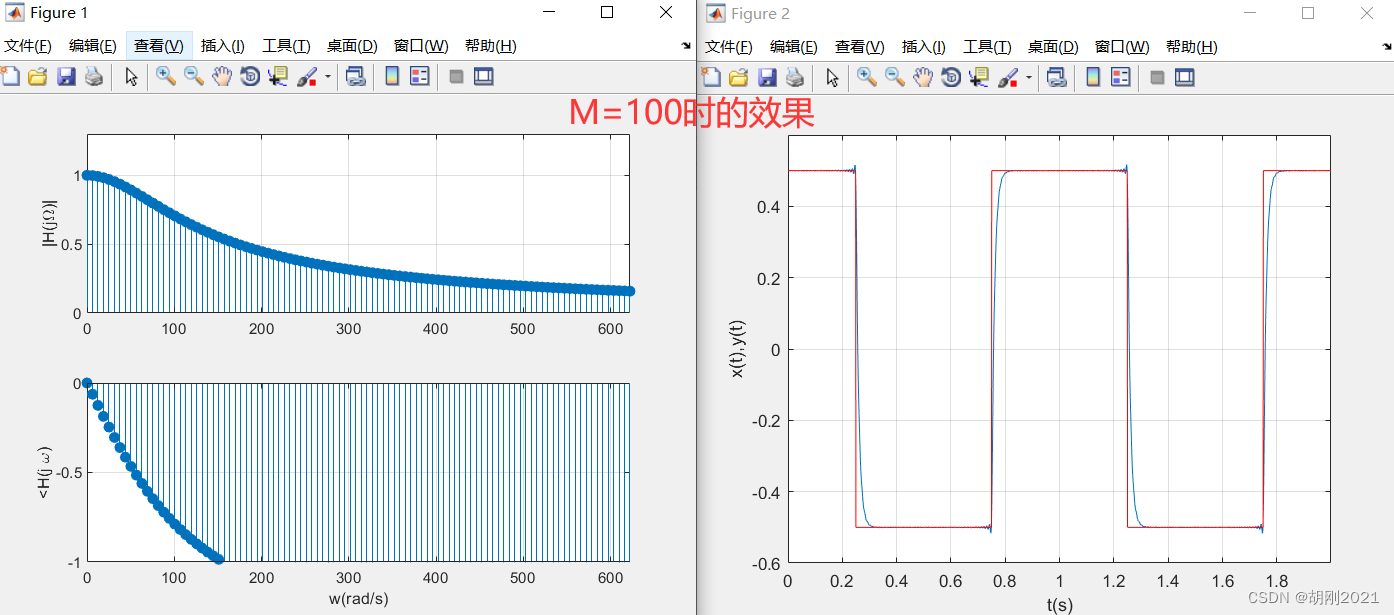
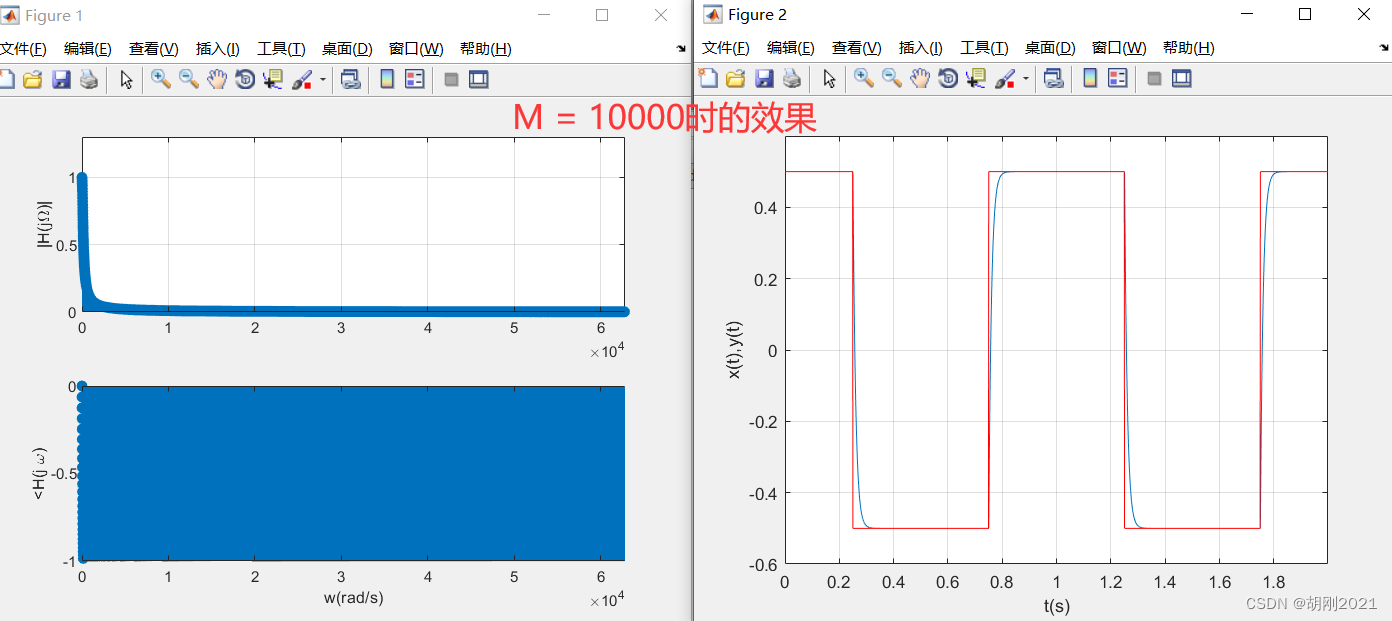
代码和运行结果

clf;
w0 = 2 * pi;
M = 1000000;
k=0:M-1;
w1=k .* w0;
H=1 ./ (1 + j *w1 /100);
Hm=abs(H);
Ha=angle(H);

subplot(211);
stem(w1, Hm, 'filled');
grid;
ylabel('|H(j\Omega)|');
axis([0 max(w1) 0 1.3]);

subplot(212);
stem(w1, Ha, 'filled');
grid;

axis([0  max(w1) -1  0]);
ylabel('<H(j \omega)');
xlabel('w(rad/s)');

%================== 以上是计算滤波器在谐波频率出的响应 =======================
%================== 以下是计算由脉冲序列x(t)引起的响应，输出的滤波信号为y(t)

figure(2);
X(1)=0;
for k = 2:M-1,
    X(k)=sin((k-1)*pi / 2)/((k-1)*pi/2);
end

Ts=0.001;
t1=0:Ts:1-Ts;
L=length(t1);
x1=[ones(1, L/4) zeros(1, L/2) ones(1, L/4)];
x1=x1 -0.5;
x=[x1 x1];

t=0:Ts:2-Ts;
y=X(1)*ones(1, length(t)) * Ha(1);
plot(t, y);
axis([0  max(t)  -.6  .6]);
for k = 2:M-1,
    y = y+X(k)*Hm(k)*cos(w0*(k-1).*t+Ha(k));
end

plot(t, y);
axis([0  max(t)  -.6 .6]);
hold on;

plot(t, x, 'r');
axis([0  max(t)  -0.6 0.6]);
grid;
ylabel('x(t),y(t)');
xlabel('t(s)');
hold off;
pause(0.1);