 齐次法( homogeneous notation )表示3D坐标: (X, Y, Z, 1)
 GLSL 数据类型中，Vec4 可以通过齐次法来表达点的坐标，同理 vec3 就是含有3个元素的元组
 GLSL 语言中，数据类型mat4 表示 4 x 4 的矩阵
 GLM 中，有一个类 class 叫 mat4，表示 4 x 4 的矩阵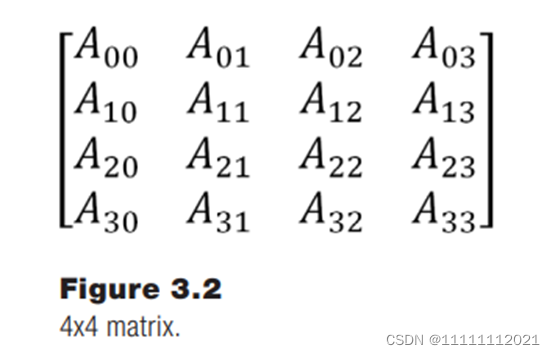

 单位矩阵：identity matrix

 在 GLM中，调用函数 glm::mat4 m(1.0f) 创造一个4x4 的单位矩阵，叫m

 转置矩阵，求 mat4的转置矩阵

		GLM中：`glm::transpose(mat4)`
			GLSL中：`transpose(mat4)`

 矩阵加法，对应位置的元素相加

			GLSL中，“`+`”

 矩阵右乘点左边，生成新的点坐标

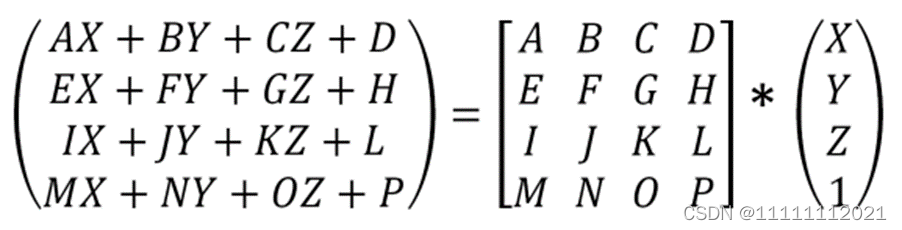
 在 GLSL 和 GLM中用 “ * ”来表示矩阵相乘
 以下两个式子相等，

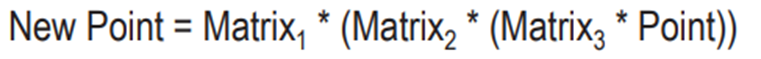
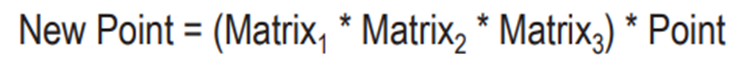
 逆矩阵，在GLM和GLSL中都是 mat4.inverse()

 变换矩阵

			平移		translation
			旋转		rotation
			缩放矩阵	scale
			投影矩阵	projection
			目视		look-at

 平移矩阵 translation

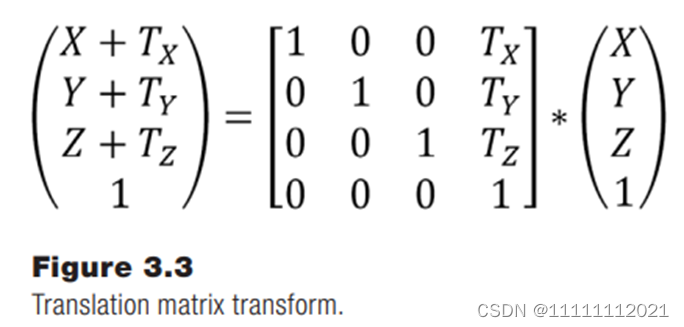
 其中，第四列的 Tx，Ty，Tz，是平移过程中的增量
 GLM中有函数能构造平移矩阵，如 mat4 = glm::translate(x,y,z) ， 然后 mat4 * vec4 得到平移后的矩阵

 缩放矩阵 scaling

 GLM 的缩放函数：mat4 = glm::scale(x,y,z); mat4 * vec4;
 左手坐标系和右手坐标系的变换矩阵（与缩放矩阵同形式）：

 旋转矩阵涉及一个坐标轴（x，y, z）和一个角度 θ

			GLM 的函数表示为： `glm::rotate(mat4, θ, x, y, z)`    // 创造经过(0,0,0)和(x,y,z)的轴线，绕着该轴旋转θ角度

 如果绕空间中的任意一个轴旋转，有三个步骤：
 ① 将这个轴线平移至经过原点
 ② 物体绕着新轴线进行旋转θ角度
 ③ 根据轴线的平移偏移量，将物体反向平移

 向量 vector

			向量可以表示为 A(u,v,w) and B(x,y,z):
				A ± B = (u ± x, v ± y, w ± z) ;
				glm: `vec3 ± vec3` 
				GLSL: `vec3 ± vec3`
			求单位向量
				glm: `normalize(vec3) or normalize(vec4)`
				GLSL: `normalize(vec3) or normalize(vec4)`
			标量积
				A ● B = ux + vy + wz 
				glm:`dot(vec3,vec3) or dot(vec4,vec4)`
				GLSL: `dot(vec3,vec3) or dot(vec4,vec4)`
			向量积

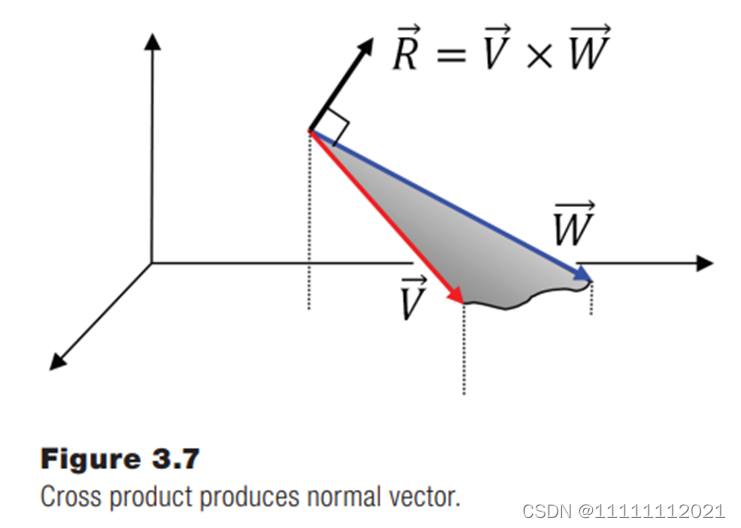
				A x B = (vz-wy, wx-uz, uy-vx) 
				glm: `cross(vec3,vec3)` 
				GLSL: `cross(vec3,vec3)`
			长度：GLSL and GLM ： `length()`

 视觉空间，eye space

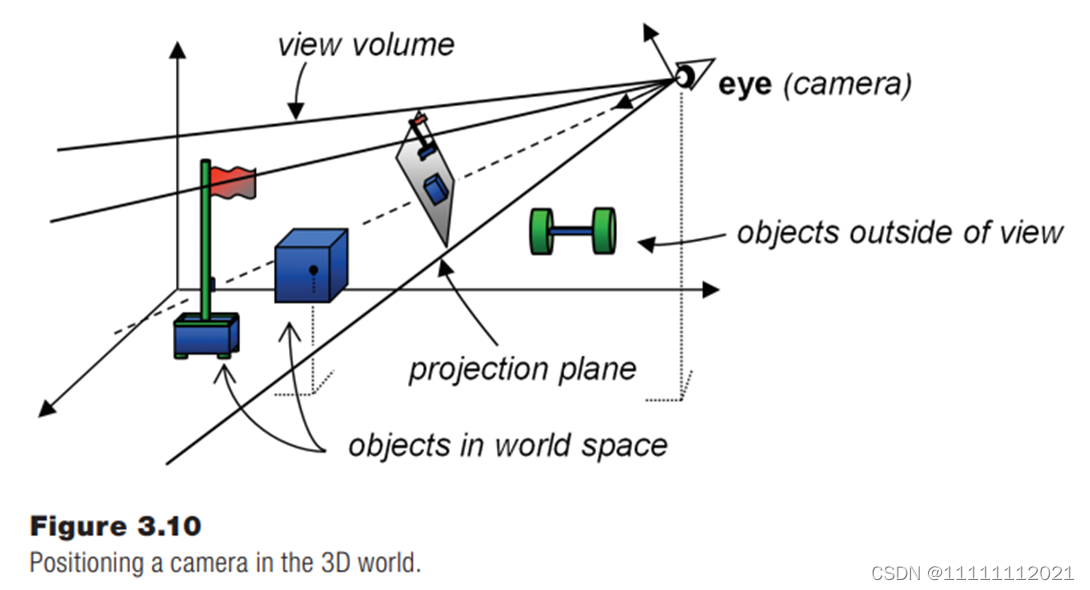
OpenGL有一个固定在远点的相机，面向z的负半轴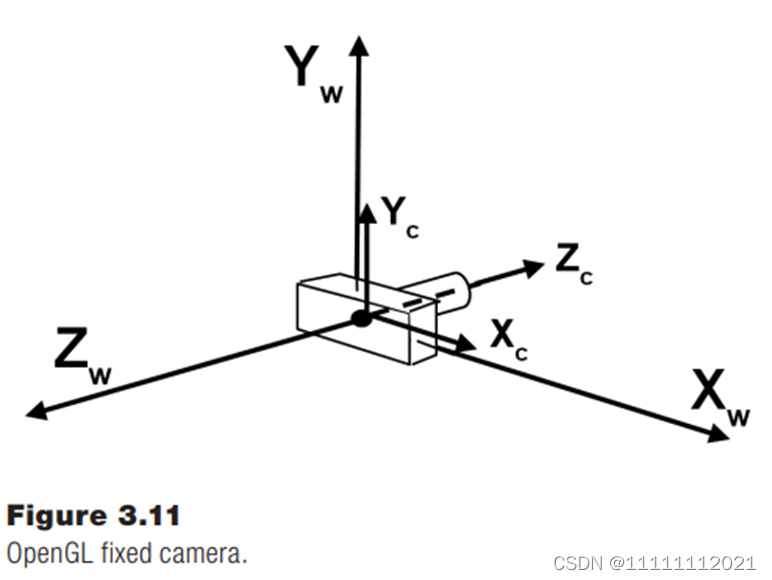

		世界坐标系下，有点Pw，需要求该点到以摄像机为坐标系的相机空间中的点坐标 Pc

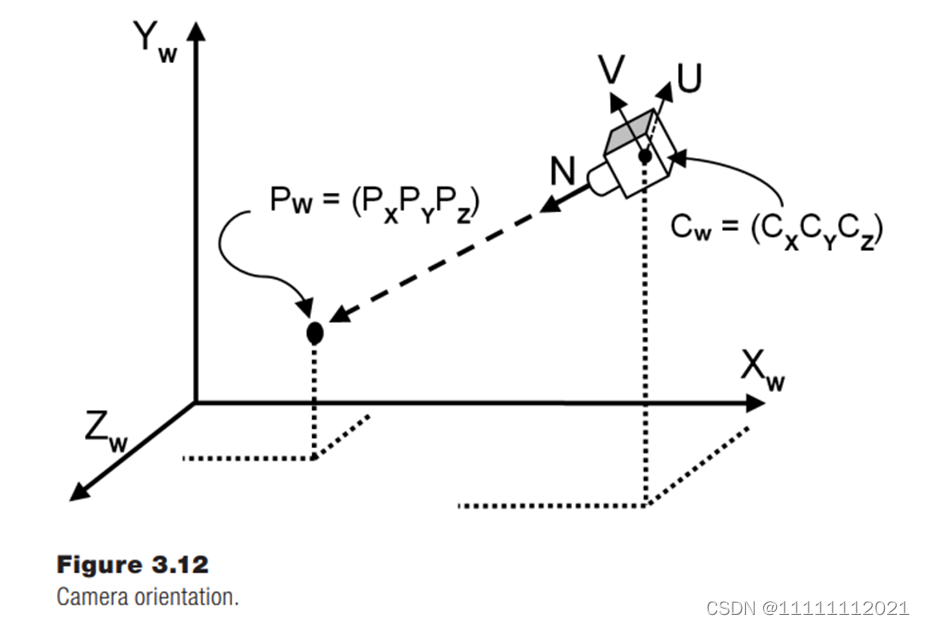
思路是：Pw 先平移，再旋转
 viewing transform matrix 检视变换矩阵 V： 矩阵中既包括旋转也包括平移信息
 V 是由 平移矩阵 T 和旋转矩阵R组成的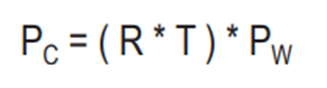

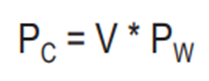
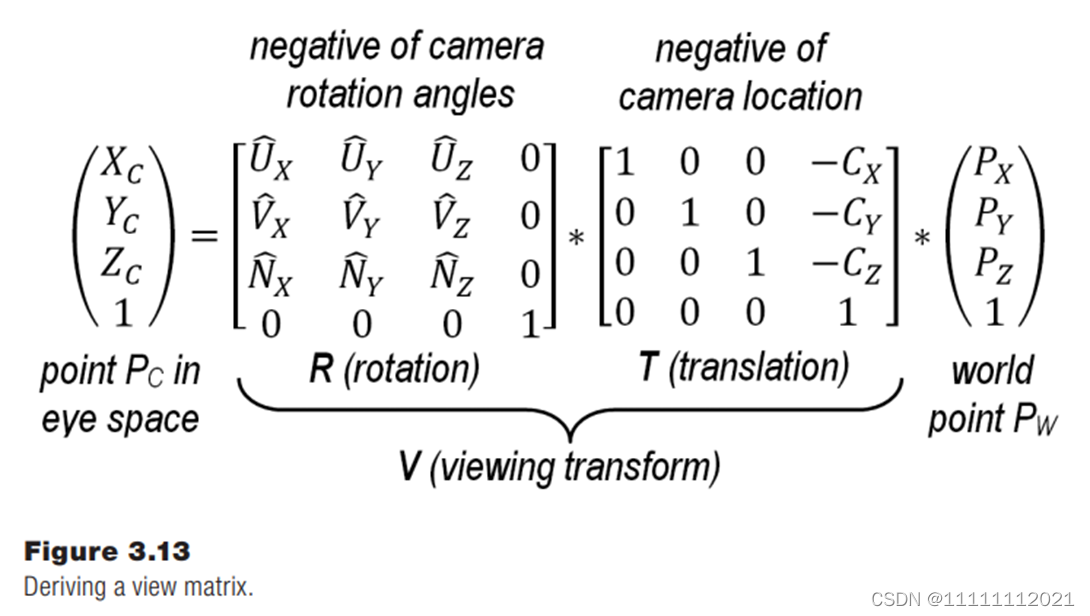
 model-view (MV) matrix ： MV = V * M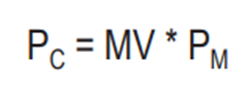

 透视矩阵 / 透视变换 perspective matrix

有四个参数：
 (a) aspect ratio, 长宽比
 (b) field of view, 视野
 © projection plane or near clipping plane, 最近投影平面
 (d) far clipping plane 最远投影平面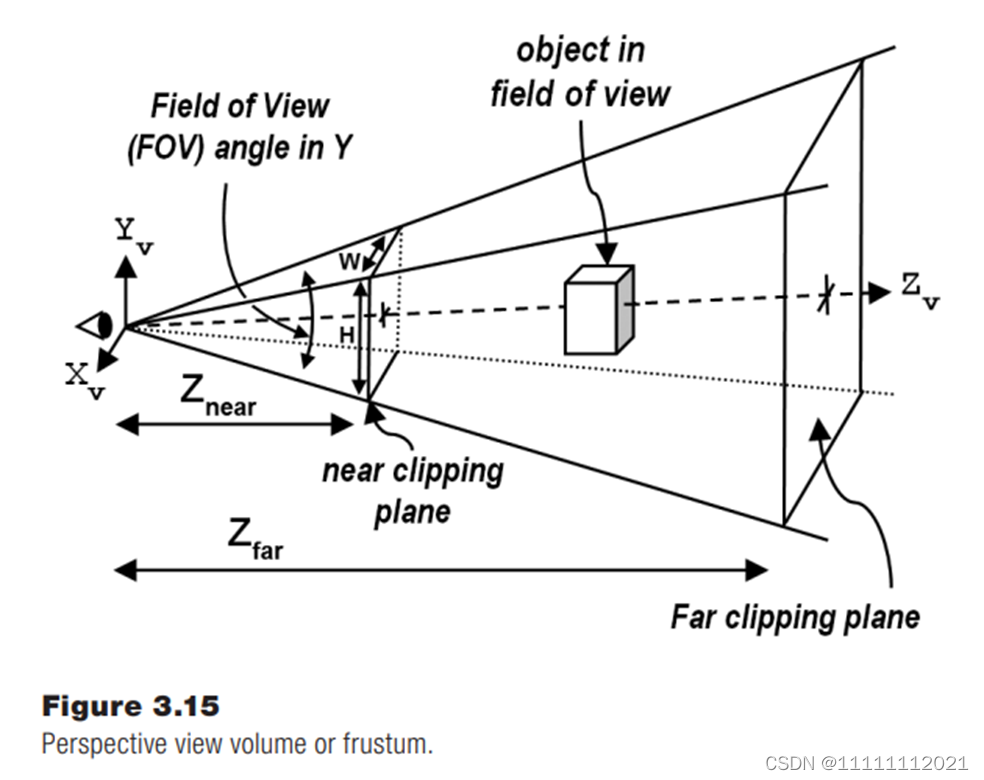

 投影矩阵的参数与矩阵

GLM的函数：glm::perspective() 用于生成透视矩阵

 正交投影矩阵The Orthographic Projection Matrix

		投影后，长度面积等都不变。这玩意是平行投影。

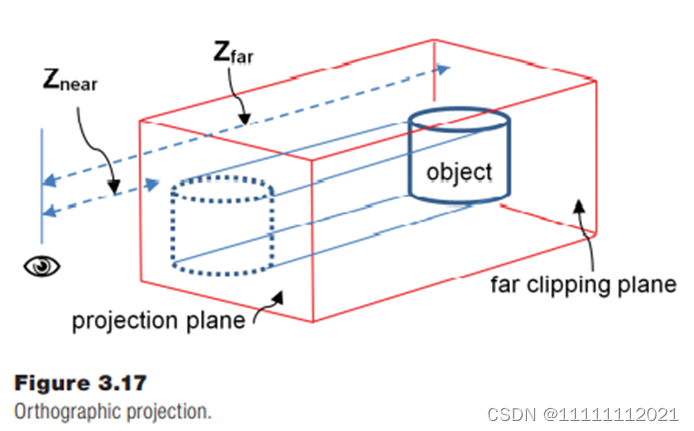
正交投影矩阵（平行投影）的参数有：
(a) the distance Znear from the camera to the projection plane,
(b) the distance Zfar from the camera to the far clipping plane,
© L, R, T, and B的值，其中 L和R是投影平面边缘最左边和最右边的x轴坐标；T和B是投影平面边缘最顶端和底端的Y轴坐标
以下是平行投影变换矩阵

 LOOK-AT MATRIX 视场矩阵

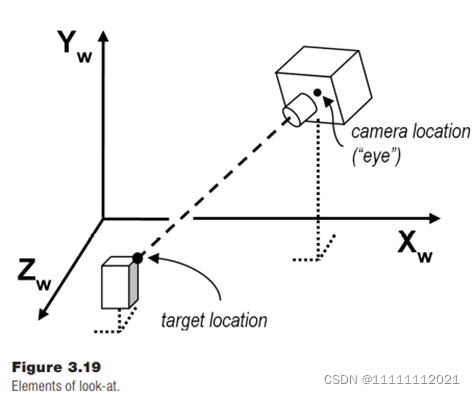
相关函数：glm::lookAt()

自定义矩阵

mat4 translationMatrix = mat4(1.0, 0.0, 0.0, 0.0,// 注意这是最左边一列，不是最上面一行
												0.0, 1.0, 0.0, 0.0,
												 0.0, 0.0, 1.0, 0.0, 
													tx, ty, tz, 1.0 );