（人脸，图像）真实的事物---》数学对象（矢量）---》矢量间的关系（数学算法或者性质，矩阵，加减法）---》另外一些矢量（特征比较明确）---》真实事物（图像，人脸）

矢量：既有长度又有方向的量

矢量相等：即两个矢量平移后可以重叠

矩阵是矢量排列： 横向排列和纵向排列

广播：不同维度的矩阵相加

向量长度：（范数：非负数，可比较，与坐标无关）

基底：被选做向量u基准的一组向量

坐标：对应各个基向量的系数

描述几何空间中的坐标点。几何空间维度由向量的成分个数决定. 描述几何空间从原点到该向量坐标点的有向线段。 值的正负性代表与坐标轴的方向是一致还是相反； 向量相加表示多个向量首尾相连，两端的起止点相连的有向线段； 向量的数乘表示向量在某方向上进行相应的倍数改变。

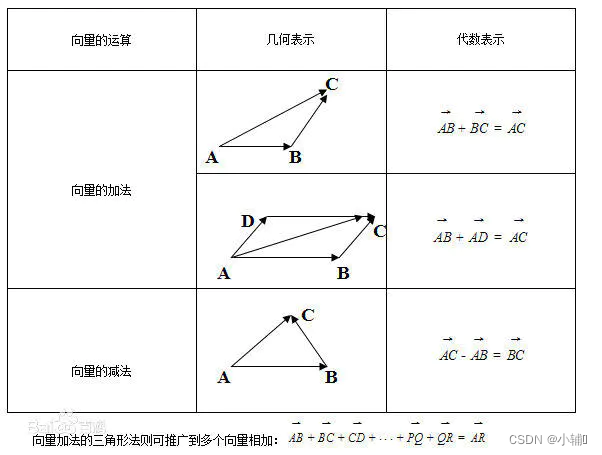
一.矢量的加法：

a=np.array([1,5])
b=np.array([4,3])
c=a+b
print(c)

c: [5,8]

用图表示就是

#矢量图像表示
import matplotlib.pyplot as plt
fig,axes=plt.subplots(1, 2, figsize=(10,5))
ax=axes[0]
ax.set_xlim([0, 20])
ax.set_ylim([0, 20])
ax.quiver(a[0],a[1],angles='xy', scale_units='xy', scale=1, color='r')
ax.quiver(a[0],a[1],c[0]-a[0],c[1]-a[1],angles='xy', scale_units='xy', scale=1, color='b')
ax.quiver(c[0],c[1],angles='xy', scale_units='xy', scale=1, color='y')
ax2=axes[1]
ax2.set_xlim([0, 5])
ax2.set_ylim([0, 10])
ax2.quiver(a[0],a[1],angles='xy', scale_units='xy', scale=1, color='r')
ax2.quiver(b[0],b[1],angles='xy', scale_units='xy', scale=1, color='b')
ax2.quiver(c[0],c[1],angles='xy', scale_units='xy', scale=1, color='y')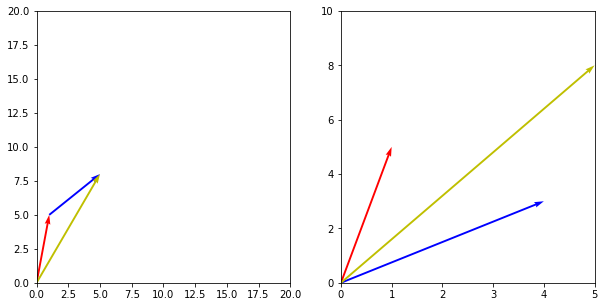

 二.矩阵的乘法

就是矩阵的乘法操作，要求左边矩阵的列和右边矩阵的行数要一致

数字与一维/二维矩阵相乘；(矩阵乘向量的几何意义: 变换基底)

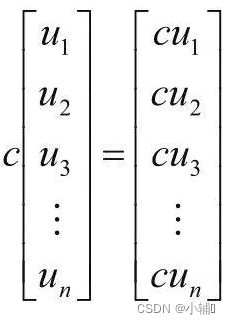
一维矩阵与一维矩阵相乘；

二维矩阵与一维矩阵相乘；

二维矩阵与二维矩阵乘；

eg:

from numpy import  *
''' 1*2 的矩阵乘以2*1 的矩阵  得到1*1 的矩阵'''

a1 = mat([1,2])
print(a1)
a2 = mat([[1],[2]])
print(a2)
a3 = a1*a2
print(a3)

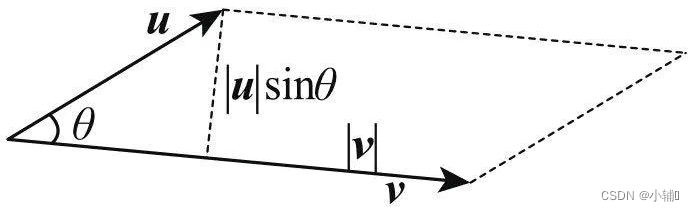
 内积的另一种表示方式: u・v=|u||v|cos(θ)