如何使用matlab实现全覆盖路径规划算法(往返式 or 弓子型)
如何使用matlab实现全覆盖路径规划算法(往返式 or 弓子型)往返式 or 弓子型全覆盖路径规划可根据任务要求建立二维栅格地图的大小,设置障碍物(位置可更改),以及起始点,根据定义往返式路径规划的定义的优先级运动规则从起始点开始进行全图遍历,利用A星(自己选择调整为4或者8临域。)算法逃离死角位置,避开障碍物寻找最近的未覆盖节点,继续进行全图覆盖,最后绘制全覆盖路径,输出搜索时间,转折点数,路
如何使用matlab实现全覆盖路径规划算法(往返式 or 弓子型)
往返式 or 弓子型全覆盖路径规划
可根据任务要求建立二维栅格地图的大小,设置障碍物(位置可更改),以及起始点,根据定义往返式路径规划的定义的优先级运动规则从起始点开始进行全图遍历,利用A星(自己选择调整为4或者8临域。)算法逃离死角位置,避开障碍物寻找最近的未覆盖节点,继续进行全图覆盖,最后绘制全覆盖路径,输出搜索时间,转折点数,路径长度等信息。
实现全覆盖路径规划算法(如往返式或弓子型)在MATLAB中可以通过以下步骤完成。我们将创建一个二维栅格地图,设置障碍物和起始点,并使用A*算法来辅助逃离死角位置,避开障碍物,寻找最近的未覆盖节点,继续进行全图覆盖。最后,我们将绘制全覆盖路径并输出相关信息。

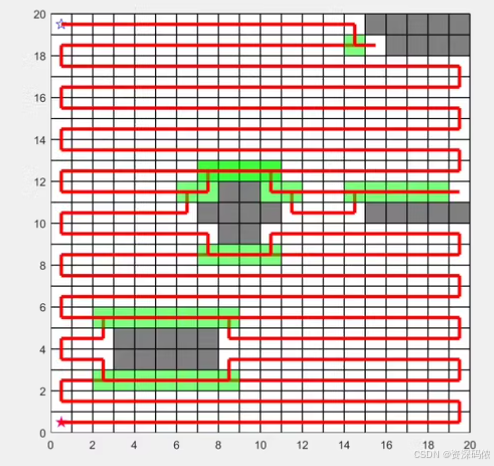
1. 创建二维栅格地图
首先,我们需要定义一个二维栅格地图,包括障碍物的位置以及起始点。
% 定义栅格地图大小
mapSize = [20, 20]; % 地图大小为20x20
map = false(mapSize); % 初始化地图,默认所有区域都可通行
% 设置障碍物
obstacles = [
5, 5;
6, 5;
7, 5;
8, 5;
9, 5];
for i = 1:size(obstacles, 1)
map(obstacles(i, 1), obstacles(i, 2)) = true; % 标记障碍物
end
% 设置起始点
startPoint = [1, 1]; % 起始点坐标
2. A*算法辅助逃离死角
接下来,我们实现A*算法来帮助机器人逃离死角,找到最近的未覆盖节点。
function path = aStarSearch(map, start, goal, neighborhood)
% A*搜索算法实现
% neighborhood: '4' 或 '8' 表示邻居节点的查找方式
% 初始化
openList = {start};
closedList = {};
cameFrom = containers.Map('KeyType', 'char', 'ValueType', 'any');
gScore = containers.Map('KeyType', 'char', 'ValueType', 'double');
gScore(char(start)) = 0;
fScore = containers.Map('KeyType', 'char', 'ValueType', 'double');
fScore(char(start)) = heuristic(start, goal);
while ~isempty(openList)
[~, currentIdx] = min(cellfun(@(node) fScore(char(node)), openList));
currentNode = openList{currentIdx};
if isequal(currentNode, goal)
return reconstructPath(cameFrom, char(goal));
end
openList(currentIdx) = [];
closedList{end+1} = currentNode;
neighbors = getNeighbors(currentNode, map, neighborhood);
for i = 1:size(neighbors, 1)
neighbor = neighbors(i, :);
if any(cellfun(@(node) isequal(node, neighbor), closedList))
continue;
end
tentativeGScore = gScore(char(currentNode)) + 1;
if ~any(cellfun(@(node) isequal(node, neighbor), openList)) || ...
tentativeGScore < gScore(char(neighbor))
cameFrom(char(neighbor)) = currentNode;
gScore(char(neighbor)) = tentativeGScore;
fScore(char(neighbor)) = gScore(char(neighbor)) + heuristic(neighbor, goal);
if ~any(cellfun(@(node) isequal(node, neighbor), openList))
openList{end+1} = neighbor;
end
end
end
end
error('No path found');
end
function h = heuristic(a, b)
% 曼哈顿距离作为启发函数
h = abs(a(1) - b(1)) + abs(a(2) - b(2));
end
function neighbors = getNeighbors(pos, map, neighborhood)
% 获取邻居节点
directions = {
[-1, 0]; [0, -1]; [1, 0]; [0, 1]; % 四邻域
[-1, -1]; [-1, 1]; [1, -1]; [1, 1] % 八邻域
};
if strcmp(neighborhood, '4')
directions = directions(1:4);
end
neighbors = [];
for i = 1:size(directions, 1)
neighborPos = pos + directions{i};
if all(neighborPos >= 1) && all(neighborPos <= size(map)) && ~map(neighborPos(1), neighborPos(2))
neighbors = [neighbors; neighborPos];
end
end
end
function path = reconstructPath(cameFrom, current)
totalPath = cell(1, 0);
while isKey(cameFrom, current)
totalPath{end+1} = str2num(current);
current = char(cameFrom(current));
end
path = fliplr(totalPath);
end
3. 实现往返式或弓子型全覆盖路径规划
基于上述A*算法,我们可以实现往返式或弓子型的全覆盖路径规划。
function fullPath = fullCoverage(map, startPoint, neighborhood)
% 初始化
coveredMap = map;
currentPos = startPoint;
fullPath = {currentPos};
turnPoints = 0;
startTime = tic;
% 遍历整个地图
while any(~coveredMap(:))
nextPos = getNextPosition(currentPos, coveredMap, neighborhood);
if isempty(nextPos)
% 使用A*算法找到最近的未覆盖节点
availableNodes = find(~coveredMap);
availableNodes = reshape(availableNodes, [], 2);
[~, nearestIdx] = min(sqrt(sum(bsxfun(@minus, availableNodes, currentPos).^2, 2)));
nextPos = aStarSearch(map, currentPos, availableNodes(nearestIdx, :), neighborhood);
else
fullPath = [fullPath, nextPos];
coveredMap(nextPos(:, 1), nextPos(:, 2)) = true;
currentPos = nextPos(end, :);
if numel(nextPos) > 1
turnPoints = turnPoints + 1;
end
end
end
% 计算搜索时间、转折点数、路径长度等信息
searchTime = toc(startTime);
pathLength = length(fullPath) - 1;
fprintf('搜索时间: %.2f秒\n转折点数: %d\n路径长度: %d\n', searchTime, turnPoints, pathLength);
end
function nextPos = getNextPosition(currentPos, coveredMap, neighborhood)
% 简化的往返式路径规划逻辑
direction = [1, 0]; % 初始方向向右
nextPos = [];
for i = 1:size(coveredMap, 1)
newPos = currentPos + direction;
if all(newPos >= 1) && all(newPos <= size(coveredMap)) && ~coveredMap(newPos(1), newPos(2))
nextPos = [nextPos; newPos];
currentPos = newPos;
else
% 改变方向
direction = -direction;
break;
end
end
nextPos = unique(nextPos, 'rows');
end
4. 绘制结果
最后,我们将绘制全覆盖路径的结果。
% 执行全覆盖路径规划
fullPath = fullCoverage(map, startPoint, '4');
% 绘制地图和路径
figure;
imagesc(map);
hold on;
plot([fullPath{:}], '-r', 'LineWidth', 2);
scatter(startPoint(2), startPoint(1), 100, 'g', 'filled');
title('全覆盖路径规划');
xlabel('X');
ylabel('Y');
legend('障碍物', '路径', '起点');
grid on;
以上代码提供了一个基本的框架来实现往返式或弓子型全覆盖路径规划。你可以根据具体需求调整和优化代码,例如改进A*算法的效率、优化路径规划策略等。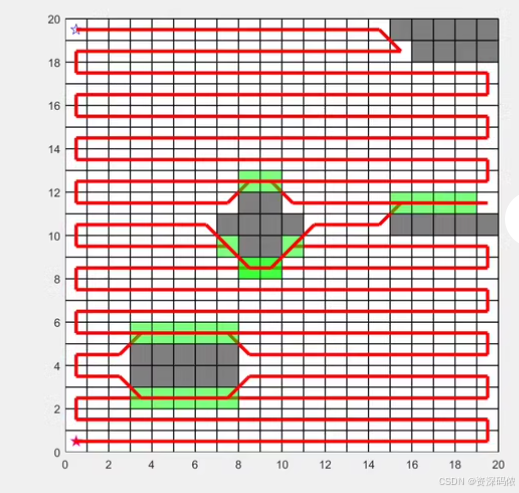

魔乐社区(Modelers.cn) 是一个中立、公益的人工智能社区,提供人工智能工具、模型、数据的托管、展示与应用协同服务,为人工智能开发及爱好者搭建开放的学习交流平台。社区通过理事会方式运作,由全产业链共同建设、共同运营、共同享有,推动国产AI生态繁荣发展。
更多推荐
 已为社区贡献6条内容
已为社区贡献6条内容







所有评论(0)