卡方分布分为中心卡方和非中心卡方。

中心卡方分布

中心卡方分布的随机变量由若干独立同分布的零均值高斯变量的平方和(也就是σ^2)得出。设有n个独立同分布的零均值高斯随机数xi~N(0,σ*σ)，i=1,2,…,n，则随机数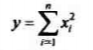

服从自由度n的中心卡方分布。自由度为n的中心卡方分布随机变量Y的期望和方差分别为

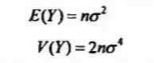
matlab对应函数

matlab给出了n个服从N(0,1)的正态分布自由度为n的中心卡方分布的计算函数:

• 卡方分布的分布函数:chi2cdf
• 分布函数的反函数chi2inv
• 概率密度函数chi2pdf
• 随机数发生函数chi2rnd
• 期望及方差计算函数chi2stat

例子：实验10个样本能否认为其期望值μ0=1600,其方差σ0^2=14400(取显著性水平α=0.02)?

数据：

1490 1440 1680 1610 1500 1750 1550 1420 1800 1580

>> x=[1490 1440 1680 1610 1500 1750 1550 1420 1800 1580];
>> m0=1600;
>> n=length(x);
>> xbar = mean(x);
>> s = std(x,1);
>> a1 = 0.02

a1 =

    0.0200

>> % 期望的假设检验
>> t1 = tinv(1-a1/2,n-1) % 自由度n-1的t分布a1/2分位点

t1 =

    2.8214 % 故均值统计量接受区间

>> t = (xbar-m0)./(s./sqrt(n-1))

t =

   -0.4427 %计算统计量t是否在接受区间

>> h_mean = (t>abs(t))

h_mean =

     0 % 接受假设

>> % 方差的假设检验
>> sig2 = 14400;
>> ch_2= chi2inv(1-a1/2,n-1)

ch_2 =

   21.6660

>> ch_1= chi2inv(a1/2,n-1)

ch_1 =

    2.0879  % 故方差统计量在接受区间为(2.0879,21.6660)

>> ch=n*s^2/(sig2)

ch =

   10.3306 % 计算统计量是否落入接受区间

>> h_var = (ch<ch_1)|(ch>ch_2)

h_var =

     0 % 接受假设

>>

非中心卡方分布

非中心卡方分布的随机变量由若干独立同方差的均值不全为0的高斯变量的平方和得出.设有n个独立的高斯随机数xi~N(mi,σ^2)，i=1,2,…n,其均值为mi,方差均为σ*σ,则其服从自由度为n的非中心卡方分布。
并设s * s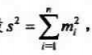

自由度为n的非中心卡方分布的随机变量Y的期望和方差分别为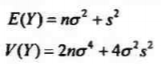

matlab对应的函数

• 非中心卡方分布的分布函数:ncx2cdf
• 非中心卡方分布函数的反函数ncx2inv
• 非中心卡方分布概率密度函数ncx2pdf
• 非中心卡方分布随机数发生函数ncx2rnd
• 非中心卡方分布期望及方差计算函数ncx2stat

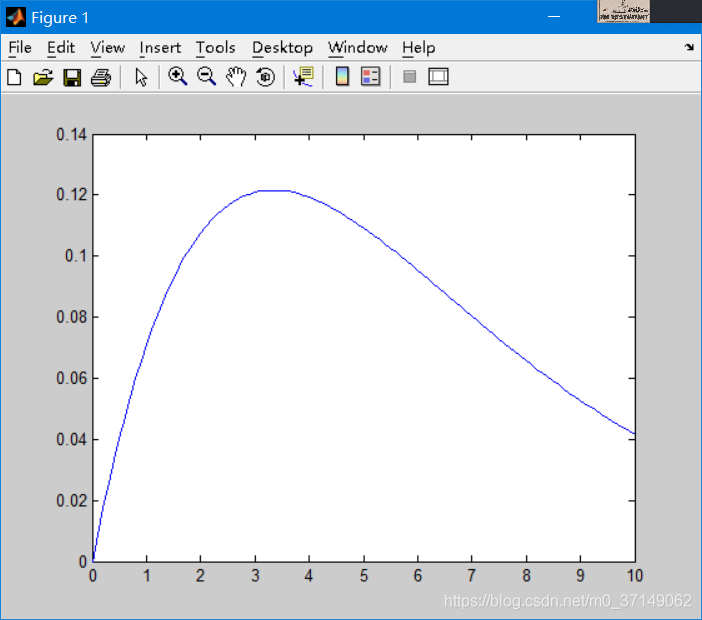
例子：绘出x∈[0,10]服从的N(4,2)非中心卡方分布

>> clear
>> x=(0:0.1:10)';
>> p1=ncx2pdf(x,4,2);
>> plot(x,p1,'-')
>> 

关于matlab的更多统计工具箱使用，可以参考此博文
matlab常见概率分布的命令函数(含例子运用)