共轭梯度法属于求解线性方程组的一种迭代法，其计算速度不算很快，但是在一些复杂的问题下，也有比较好的下效果，因为科研需要，根据理论编写了一下共轭梯度法的程序，特此分享：

1、原理步骤如下：

2、 编程的流程如下：

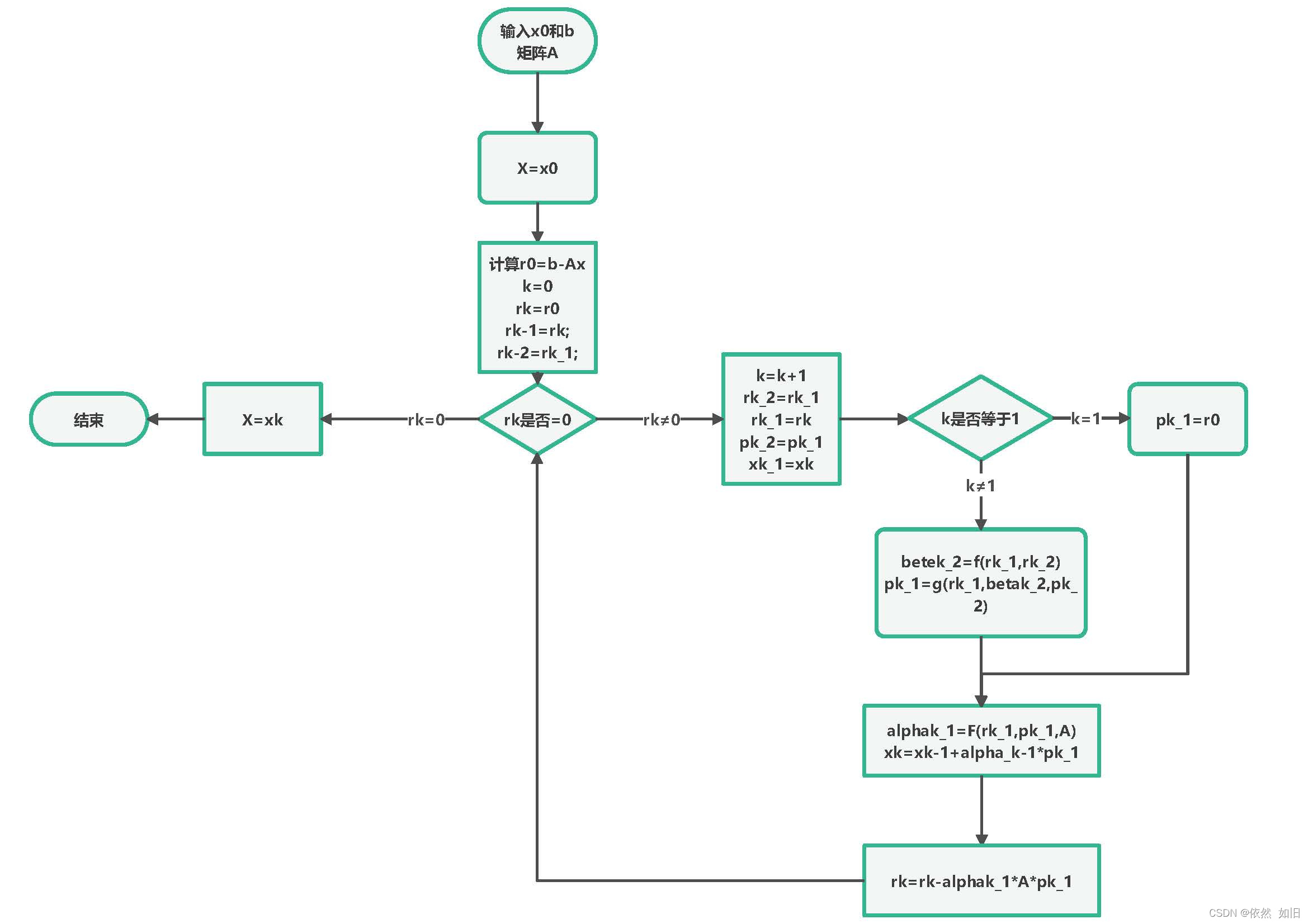
3、程序如下：

function [x] = CG_solver(A,b,x0,kmax)
%使用共轭梯度法求解 A · X = b线性方程组
% A方程组系数矩阵 b系数项 X0是迭代的初值（0向量就可以） kmax最多迭代次数
%   wrote by Han JIale in 2022.07.04
xk=x0;
%附上初值
r0=b-A*xk;
k=0;
rk=r0;
rk_1=rk;
rk_2=rk_1;
pk_1=r0;


while sqrt(sum(rk.^2))>=10^(-5) && (k<kmax) %停机准则，可以修改
    k=k+1;
    rk_2=rk_1;
    rk_1=rk;
    pk_2=pk_1;
    xk_1=xk;
    if k==1
        pk_1=r0;
    else
        betek_2=(rk_1'*rk_1)/(rk_2'*rk_2);
        pk_1=rk_1+betek_2*pk_2;
    end
    alphak_1=(rk_1'*rk_1)/(pk_1'*A*pk_1);
    xk=xk_1+alphak_1*pk_1;
    rk=rk-alphak_1*A*pk_1;

end
x=xk;
end